授导型教学设计教案案例
- 格式:doc
- 大小:123.00 KB
- 文档页数:11
《Who is dancing》授导型教学设计章节名称Unit3 Lesson 1授课班学科英语九年级授课时数1级所属学九支中学设计者段海燕校本节(课)教学内容分析《Who is danding?》是冀教版义务教育课程标准实验教科书英九年级下册第一单元《On the train 》中的内容。
本单元内容围绕丹尼、詹妮、李明和李明的妈妈在火车上的所见所闻展开,内容贴近生活,句型较宜理解掌握。
依据标准课程标准:全日制义务教育英语课程标准(实验稿)1--9年级学段:知识与技能第二条,数学思考第二条,解决问题第二条、第三条、第四条教育技术标准:本节(课)教学目标知识目标:对本课单词baby man woman;句型Who is this? This is a man.做到听说读写四会。
能听懂说出认读单词their 能够理解并表演第二部分:Who is singing?能力目标:通过学习本课,能掌握相关的词汇;用简单的语言描述人物,描述人物的活动,表达自己的感受;用现在进行时描述。
情感目标:通过和Li Ming, Jenny, Danny在火车上的活动,增强学生观察力,增加生活情趣,更加热爱生活。
学习者特征分析一般特征:1.学生是九支中学九年级学生;2.学生胆小,不爱在课堂上发言。
3.九年级的学生,较不喜欢枯燥的讲解和分析,他们喜欢游戏式的课堂教学。
初始能力:1.学习了前两课后,已对要学习内容的发生环境了解的很清楚;2.学生对要四会的单词接触到过;3.对句型较熟悉。
信息素养:知识点学习目标描述知识点编号学习目标具体描述语句1听说读写四会十五个重点单词2认读认读五个单词3理解理解课文内容4运用运用句型进行对话教学重点和难点项目内容解决措施教学重点本课的四会单词:man, woman, baby句型:Who is ___?It’s ____.让学生先回忆已经见到的单词,多读,根据读音记住单词的形,句子的掌握要通过多用,做练习。



模块4-1教学设计表学科数学授课年级三年级学校矾山镇第二小学教师姓名罗平平章节名称人教版小学数学三年级上册《有余数的除法》计划学时1学习内容分析“有余数的除法”是小学数学第五册第四单元的知识。
本单元知识可分为两块:一是有余数除法的意义、竖式计算有余数的除法及余数和除数的关系;一是用有余数除法的知识解决问题。
这部分内容是表内除法知识的延伸和扩展,是今后学习一位数除多位数除法的重要基础,因此这部分的知识具有承上启下的作业。
本节课的教学内容主要是有余数除法的意义,掌握正确的计算方法并会用竖式进行除法的计算。
学习者分析学生在二年级时已经学过表内乘除法,熟练地掌握表内乘除法并正确地计算是本单元学习的基础。
另外,除法平均分的现象在生活中非常常见,二年级学习除法时解决的是正好分完的情况,而有余数的除法解决的是平均分后有剩余的情况。
正确理解余数的意义,正确计算有余数的除法是本单元教学的重点。
教学目标课程标准:数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。
数学教学,要紧密联系学生的生活实际,从学生的生活经验和已有知识出发,创设生动有趣的情境,引导学生开展观察、操作、猜想、推理、交流等活动,使学生通过数学活动,掌握基本的数学知识和技能,初步学会从数学的角度去观察事物、思考问题,激发对数学的兴趣,以及学好数学的愿望。
知识与技能:结合分一分的活动,使学生感知有余数除法的意义,掌握除法试商的方法,会用竖式进行正确的计算,并知道竖式中各部分的名称。
过程与方法:通过分糖活动,动手操作,观察等数学活动,理解有余数除法的意义,掌握试商的方法,培养学生的分析、综合、抽象概括的能力。
情感、态度与价值观:培养学生数学学习的兴趣,建立数学学习的信心,体会数学与生活的紧密联系。
教学重点及解决措施重点:1.感知有余数除法的意义,初步掌握有余数除法的计算方法。
2.会用竖式进行计算,并知道竖式中各部分的名称。
解决措施:通过动手操作分一分、圈一圈等活动感知生活中平均分时有剩余的情况,并在实际操作中掌握试商的方法。

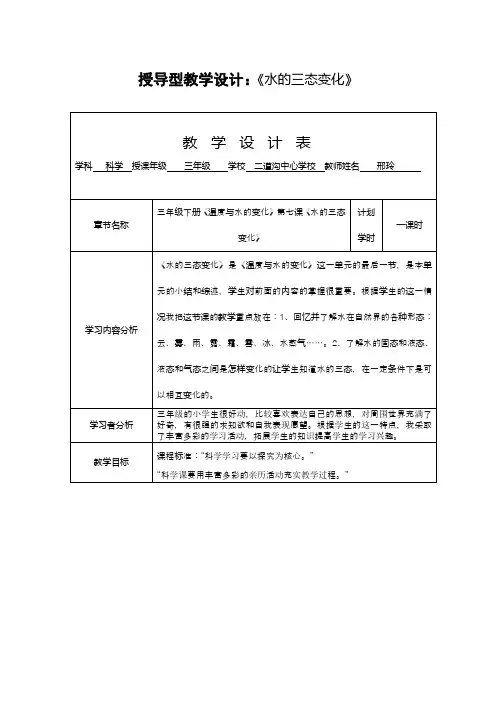
授导型教学设计:《水的三态变化》
个环节之后再回过来回答也可以。
)
二、水的三态循环
1、小结:我们刚才通过的讨论和前面几课的实验和观察,发现了液态的水能凝固成固态的冰,固态的冰会融化成液态的水,液态的水会蒸发成气态的水蒸气,气态的水蒸气又会凝结成液态的水。
师:你能用图来表示上面三者之间的转化吗?(学生画)
(预设:(1)如果前面学生没有讨论出霜和雪的变化过程,这里可以再问一句:师:那么固态的冰和气态的水蒸气之间能互相转化吗?霜和雪是从水的什么状态变化而来的?在什么条
件下形成的?如果学生还是不理解可以教师演示一个实验:在一只干燥的玻璃烧杯里装满小冰块,并往碎冰里加入大量的食盐,过几分钟后可以看到玻璃杯外壁上有固态的冰晶出现。
然后请学生解释现象:空气中的水蒸气,遇到了冷的玻璃杯壁(低于0℃),从而凝华成了冰晶。
)(2)如果刚才讨论出了就可以在上面的总结中直接总结完整。
)
热量的变化引起了水的三态变化。
2、师:我们学了这么多之后,现在你能解释为什么海洋中的总不会溢出,河流中的水一直流不完吗?请同学们结合P58的图,讨论一下。
3、交流。
三、拓展1、师:学了这章,你有什么收获呢?2、阅读资料库,增长知识。
四、板书设计。
一、教学目标1. 知识目标:通过本节课的学习,学生能够掌握授导式教学的基本概念、特点、原则和方法。
2. 能力目标:培养学生运用授导式教学方法进行教学设计的能力,提高学生的教学设计水平。
3. 情感目标:激发学生对授导式教学方法的兴趣,增强学生的教育责任感。
二、教学内容1. 授导式教学的基本概念2. 授导式教学的特点3. 授导式教学的原则4. 授导式教学方法5. 授导式教学设计步骤三、教学过程1. 导入新课(1)教师简要介绍授导式教学的概念,激发学生的学习兴趣。
(2)通过提问,引导学生思考授导式教学的特点和原则。
2. 讲解授导式教学的基本概念(1)教师详细讲解授导式教学的基本概念,包括其起源、发展、应用等方面。
(2)结合实例,帮助学生理解授导式教学的基本概念。
3. 分析授导式教学的特点(1)教师引导学生分析授导式教学的特点,如互动性、针对性、实践性等。
(2)通过小组讨论,让学生进一步了解授导式教学的特点。
4. 讲解授导式教学的原则(1)教师详细讲解授导式教学的原则,如目标导向、学生中心、合作学习等。
(2)结合实例,让学生了解这些原则在实际教学中的应用。
5. 授导式教学方法(1)教师介绍授导式教学方法,如讲授法、讨论法、案例分析等。
(2)通过示范教学,让学生了解这些方法的具体操作。
6. 授导式教学设计步骤(1)教师引导学生掌握授导式教学设计步骤,包括确定教学目标、设计教学内容、选择教学方法、制作教学课件等。
(2)让学生分组进行教学设计,并分享设计心得。
7. 总结与反思(1)教师对本节课的内容进行总结,强调授导式教学的重要性。
(2)引导学生反思自己在授导式教学设计过程中的收获与不足。
四、教学评价1. 课堂表现:观察学生在课堂上的参与程度、讨论积极性、问题回答等。
2. 教学设计:评估学生的授导式教学设计方案,包括设计思路、教学方法、教学内容等。
3. 反馈与改进:收集学生对授导式教学设计的意见和建议,不断改进教学方法。
授导型教学设计教案案例 发布者: 戴鲁伟 发布时间: 2011-12-12 13:37:20
教学设计表 学科 数学 科学 授课年级 初二年级 学校 德惠市十五中 教师姓名 刘廷斌
章节名称 15.3中心对称 计划学时 1
学习内容分析 本课是《中心对称》的第一课时,内容包括中心对称的概念、性质及应用。属于八年级几何的重要内容之一,这一节课与轴对称图形的基本概念、性质有着紧密的联系,同时与图形的三种运动(平移、翻折、旋转)之一的“旋转”有着不可分割的联系。本课起到了承上启下的作用,同时还是学生从学习“认知几何”到“认证几何”的重要过渡阶梯。
教学目标 知识与技能:掌握两个概念,了解一个性质,熟练一种作图 过程与方法:经历概念形成的过程,自己探索中心对称的性质,通过实践去感受旋转的运动变换的数学思想。 情感、态度与价值观:让学生体验到成功的喜悦,树立自信心,体验与他人合作的重要性,感受数学美,明白数学来源于生活又服务于生活的道理。
教学重点及解决措施 教学重点及确定的理由:掌握概念是应用的基础,只有理解了概念,才能准确
判断,才能正确运用,所以教学重点是中心对称图形与中心对称概念及性质。
教学难点及解决措施
教学难点及确定的依据(及解决办法):在实践教学中,学生往往对概念不做
深刻的理解,实际应用起来就会发现有许多不明白的地方,根子就在于对其概念与性质的真正理解上。所以教学难点是对中心对称图形与中心对称的区别与联系。
教学设计思路 、魔术引入 、探究新知 1、 指导观察,揭示中心对称图形的概念。
2、教学中心对称的概念,比较归纳中心对称与中心对称图形的区别与联系。 3、探索中心对称的性质。 三、教学例题 画出△ABC关于点O成中心对称的图形。 四、课堂小结
依据的理论 迪克-凯瑞模式
信息技术应用分析 知识点 学习水平 媒体内容与形式 使用方式 使用效果 中心对称图形 认知
多媒体
PPT展示 良好
中心对称 初步掌握 实验演示 独立操作 良好
中心对称的性质 掌握 网络资源 独立操作; 资源整合; 良好
教学过程(可续页) 教学环节 教学内容 所用时间 教师活动 学生活动 设计意图
课前准备 生活中的热的传递 课间 布置任务 完成任务 为新课准备;
问题引导 魔术 5分钟 具体做法:用几张里非中心对称图形的扑克牌和一张是中心对称图形的扑克牌,设置一个小小的魔术:把牌放在桌上,然后闭上眼睛,请一位同学上前,把某一张牌旋转180度后放好。老师睁开眼睛后,能很快确定哪一张是被旋转过的。问:这是为什么?你能当这个魔术师吗?你想当吗? 学生配合 我设计了一个魔术,用来导入新课,目的是设置悬念,激发兴趣,让学生观察、猜想、发现。
新课 中心对称图形 15分钟
上节课我们学习了旋转对称图形,什么是旋转对称图形呢? 老师让同学们自己做的旋转对称图形,大家做好了吗,让我们共同欣赏一下吧! 一个图形绕着某一定点旋转一定的角度(小于周角)后能与自身重合,这样的图形叫做旋转对称图形。 生(师板书):一个图形围绕中心点旋转 学生展示各种各样的旋转对称图形,教师让学生说出旋转多少度能与自身重合。再把几个旋转180度能与自身重合的展示在黑板上,并问,这些图形有什么共同特点呢?我们把这些图形称为中心对称图形,谁能说说什么是中心对称图形呢? 师强调中心对称图形是特殊的旋转对称图形。 180度后能与自身重合,我们把这种图形叫做中心对称图形。 这个中心点叫做对称中心。 举出几个例子来判断,并说出对称中心的位置。(线段、等边三角形、长方形、正方形、圆、平行四边形。)
新课二 中心对称 15分钟 动手画出一个平行四边形,观察连接对角线后形成的对着的两个三角形,你能发现这两个三角形有什么特点 ?学生不难发现,一个三角形绕对角线交点旋转180度后与另一个三角形重合,引出中心对称的概念 以小组为单位,找出成中心对称的两个图形中的等量关系,进一步归纳出中心对称的性质。 探索:教材17页图11.3.3中,△ ABC与 △ A’B’C’ 是关于点O成中心对称的,你能从图中找到哪些等量关系?(学生活动,4人一小组参与讨论,各抒己见,找代表回答,教师参与学生的讨论,并注意帮助个别学生分析图中的等量关系。)学生讨论交流后,归纳出中心对称的基本性质,并填入练习卡内 学生观察、讨论,自主探索中心对称的性质 理论联系实际 小结 5分钟 本课我们认识了中心对称,实际上,对称的内涵远超出了数学的范畴,它出现在自然、艺术(建筑)、科学乃至诗歌里。对称是一种美,没有对称不一定不美,但有了对称生活会更美。在美的音乐声中完成思考:这节课你学到了什么?发现了什么?找到了什么?……(点评:给学生留出时间回顾、思考,让学生畅所欲言,培养学生的语言表达能力和概括能力) 学生总结 提高学生的归纳概括能力
授导型教学设计教案案例 授导型教学设计教案案例 发布者: 戴鲁伟 发布时间: 2011-12-12 13:37:20
教学设计表 学科 数学 科学 授课年级 初二年级 学校 德惠市十五中 教师姓名 刘廷斌
章节名称 15.3中心对称 计划学时 1
学习内容分析 本课是《中心对称》的第一课时,内容包括中心对称的概念、性质及应用。属于八年级几何的重要内容之一,这一节课与轴对称图形的基本概念、性质有着紧密的联系,同时与图形的三种运动(平移、翻折、旋转)之一的“旋转”有着不可分割的联系。本课起到了承上启下的作用,同时还是学生从学习“认知几何”到“认证几何”的重要过渡阶梯。
教学目标 知识与技能:掌握两个概念,了解一个性质,熟练一种作图 过程与方法:经历概念形成的过程,自己探索中心对称的性质,通过实践去感受旋转的运动变换的数学思想。 情感、态度与价值观:让学生体验到成功的喜悦,树立自信心,体验与他人合作的重要性,感受数学美,明白数学来源于生活又服务于生活的道理。
教学重点及解决措施 教学重点及确定的理由:掌握概念是应用的基础,只有理解了概念,才能准确
判断,才能正确运用,所以教学重点是中心对称图形与中心对称概念及性质。
教学难点及解决措施
教学难点及确定的依据(及解决办法):在实践教学中,学生往往对概念不做
深刻的理解,实际应用起来就会发现有许多不明白的地方,根子就在于对其概念与性质的真正理解上。所以教学难点是对中心对称图形与中心对称的区别与联系。
教学设计思路 、魔术引入 、探究新知 1、 指导观察,揭示中心对称图形的概念。
2、教学中心对称的概念,比较归纳中心对称与中心对称图形的区别与联系。 3、探索中心对称的性质。 三、教学例题 画出△ABC关于点O成中心对称的图形。 四、课堂小结
依据的理论 迪克-凯瑞模式
信息技术应用分析 知识点 学习水平 媒体内容与形式 使用方式 使用效果 中心对称图形 认知
多媒体
PPT展示 良好
中心对称 初步掌握 实验演示 独立操作 良好
中心对称的性质 掌握 网络资源 独立操作; 资源整合; 良好
教学过程(可续页) 教学环节 教学内容 所用时间 教师活动 学生活动 设计意图
课前准备 生活中的热的传递 课间 布置任务 完成任务 为新课准备;
问题引导 魔术 5分钟 具体做法:用几张里非中心对称图形的扑克牌和一张是中心对称图形的扑学生配合 我设计了一个魔克牌,设置一个小小的魔术:把牌放在桌上,然后闭上眼睛,请一位同学上前,把某一张牌旋转180度后放好。老师睁开眼睛后,能很快确定哪一张是被旋转过的。问:这是为什么?你能当这个魔术师吗?你想当吗? 术,用来导入新课,目的是设置悬念,激发兴趣,让学生观察、猜想、发现。
新课 中心对称图形 15分钟 上节课我们学习了旋转对称图形,什么是旋转对称图形呢? 老师让同学们自己做的旋转对称图形,大家做好了吗,让我们共同欣赏一下吧! 学生展示各种各样的旋转对称图形,教师让学生说出旋转多少度能与自身重合。再把几个旋转180度能与自身重合的展示在黑板上,并问,这些图形有什么共同特点呢?我们把这些图形称为中心对称图形,谁能说说什么是中心对称图形呢? 师强调中心对称图形是特殊的旋转对称图形。 一个图形绕着某一定点旋转一定的角度(小于周角)后能与自身重合,这样的图形叫做旋转对称图形。 生(师板书):一个图形围绕中心点旋转180度后能与自身重合,我们把这种图形叫做中心对称图形。 这个中心点叫做对称中心。 举出几个例子来判断,并说出对称中心的位置。(线段、等边三角形、长方形、正方形、圆、平行四边形。) 新课二 中心对称 15分钟 动手画出一个平行四边形,观察连接对角线后形成的对着的两个三角形,你能发现这两个三角形有什么特点 ?学生不难发现,一个三角形绕对角线交点旋转180度后与另一个三角形重合,引出中心对称的概念 以小组为单位,找出成中心对称的两个图形中的等量关系,进一步归纳出中心对称的性质。 探索:教材17页图11.3.3中,△ ABC与 △ A’B’C’ 是关于点O成中心对称的,你能从图中找到哪些等量关系?(学生活动,4人一小组参与讨论,各抒己见,找代表回答,教师参与学生的讨论,并注意帮助个别学生分析图中的等量关系。)学生讨论交流后,归纳出中心对称的基本性质,并填入练习卡内 学生观察、讨论,自主探索中心对称的性质 理论联系实际