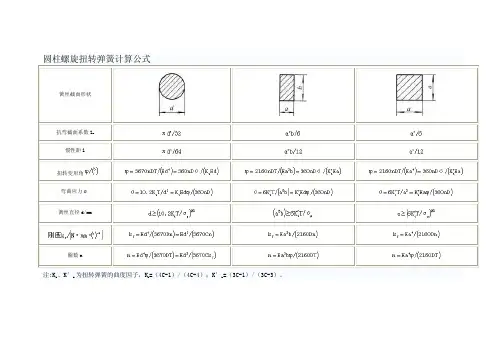
圆柱螺旋扭转弹簧计算公式

弹簧圈数的确定有效圈数是指弹簧能保持相同节距的圈数。

弹簧有效圈数的计算：总圈数—支撑圈，具体根据结构进行计算。

对于拉伸弹簧，有效圈数n＝总圈数n1，当n> 20时圆整为整数圈，当n<20时圆整为半圈。

对于压缩弹簧，有效圈数n为总圈数n1减去支撑圈数n2，n2可查表获得。

尾数应为1/4、1/ 2、3/4、或整圈，推荐1/2圈。

建议你查看GB 1973．1－89 《小型圆柱螺旋弹簧技术条件》中华人民共和国机械电子工业部1989－03－02批准1990－01－01实施小型圆柱螺旋弹簧技术条件GB 1973．1－89中华人民共和国机械电子工业部1989－03－02批准1990－01－01实施1 主题内容与适用范围木标准规定丁小型圆柱螺旋弹簧的技术要求、试验方法和检验规则。

本标准适用于圆截面圆柱螺旋压缩、拉伸和扭转弹簧(以下简称弹簧)。

弹簧材料的截面直径小于0．5 mm。

本标准不适用于特殊性能的弹簧。

2 引用标准GB 191 包装储运图示标志GB 1239．5 圆柱螺旋弹簧抽样检查GB 1805 弹簧术语GB 2828 逐批检查计数抽样程序及抽样表(适用于连续批的检查)GB 3123 硅青铜线GB 3124 锡青铜线GB 3134 铍青铜线GB 4357 碳素弹簧钢丝GB 4358 琴钢丝GB 4459．4 机械制图弹簧画法GB 4879 防锈包装GB 6543 瓦楞纸箱YB(T) 11 弹簧用不锈钢丝3 技术要求3．1 产品应符合本标准的要求，并按经规定程序批准的产品图样及技术文件制造。

3．2 极限偏差的等级弹簧特性与尺寸的极限偏差分为1、2、3三个等级。

各项目的等级应根据使用需要分别独立选定，并在图样上注明，未注明的则由制造厂从标准中选定。

3．3 压缩和拉伸弹簧的弹簧特性及其极限偏差3．3．1 弹簧特性压缩(或拉伸)弹簧的弹簧特性为指定高度(或长度)的负荷或刚度。

3．3．1．1 在指定高度(或长度)的负荷下，弹簧的变形量应在试验负荷时变形量的20％～80％之间。

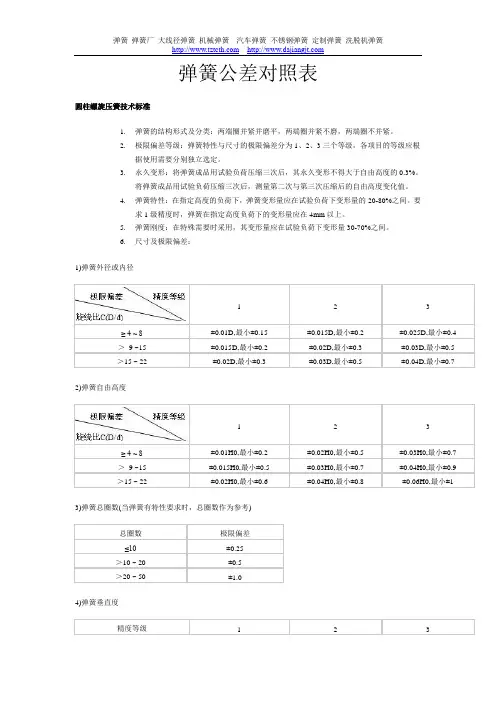
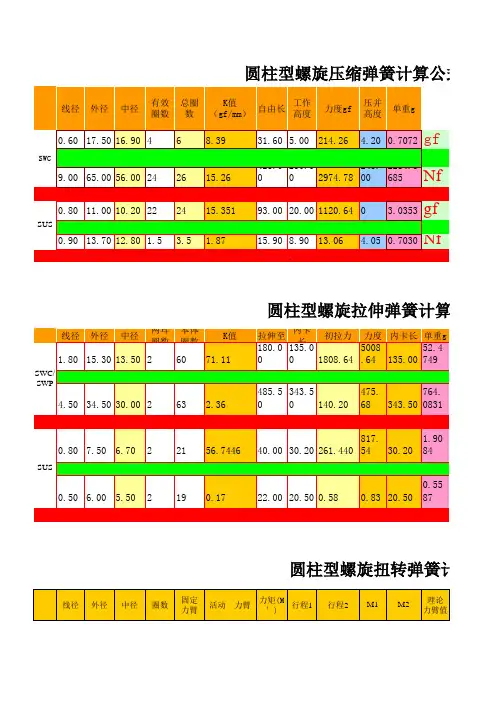
弹簧公差对照表圆柱螺旋压簧技术标准1.弹簧的结构形式及分类：两端圈并紧并磨平，两端圈并紧不磨，两端圈不并紧。

2.极限偏差等级：弹簧特性与尺寸的极限偏差分为1、2、3三个等级，各项目的等级应根据使用需要分别独立选定。

3.永久变形：将弹簧成品用试验负荷压缩三次后，其永久变形不得大于自由高度的0.3%。

将弹簧成品用试验负荷压缩三次后，测量第二次与第三次压缩后的自由高度变化值。

4.弹簧特性：在指定高度的负荷下，弹簧变形量应在试验负荷下变形量的20-80%之间。

要求1级精度时，弹簧在指定高度负荷下的变形量应在4mm以上。

5.弹簧刚度：在特殊需要时采用，其变形量应在试验负荷下变形量30-70%之间。

6.尺寸及极限偏差：1)弹簧外径或内径1 2 3≥ 4 ~ 8±0.01D,最小±0.15 ±0.015D,最小±0.2 ±0.025D,最小±0.4＞9 ~15 ±0.015D,最小±0.2 ±0.02D,最小±0.3 ±0.03D,最小±0.5＞15 ~ 22 ±0.02D,最小±0.3 ±0.03D,最小±0.5 ±0.04D,最小±0.7 2)弹簧自由高度1 2 3≥ 4 ~ 8±0.01H0,最小±0.2 ±0.02H0,最小±0.5 ±0.03H0,最小±0.7＞9 ~15 ±0.015H0,最小±0.5 ±0.03H0,最小±0.7 ±0.04H0,最小±0.9＞15 ~ 22 ±0.02H0,最小±0.6 ±0.04H0,最小±0.8 ±0.06H0,最小±1 3)弹簧总圈数(当弹簧有特性要求时，总圈数作为参考)总圈数极限偏差≤10±0.25＞10 ~ 20 ±0.5＞20 ~ 50 ±1.04)弹簧垂直度精度等级 1 2 3垂直度0.02H0(1°26′)0.05H0(2°52′)0.08H0(4°34′) 5)指定高度时的负荷P的极限偏差1 2 3≥ 3 ~ 10±0.05P ±0.10P ±0.15P＞10 ±0.04P ±0.08P ±0.12P6)弹簧刚度P′的极限偏差1 2 3≥ 3 ~ 10±0.05P′±0.10P′±0.15P′＞10 ±0.04P′±0.08P′±0.12P′7）节距：等节距的弹簧在压缩到全变形量的80%时，其正常节距圈不得接触。

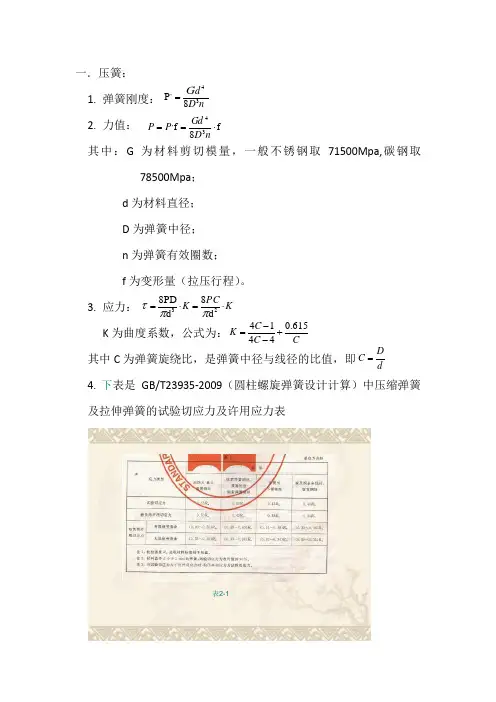
1. 弹簧刚度：
2. 力值： 其中：G 为材料剪切模量，一般不锈钢取71500Mpa,碳钢取
78500Mpa ；
d 为材料直径；
D 为弹簧中径；
n 为弹簧有效圈数；
f 为变形量（拉压行程）。

3. 应力： K 为曲度系数，公式为： 其中C 为弹簧旋绕比，是弹簧中径与线径的比值，即
4. 下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力，加上初拉力就行。

初拉力： 其中初拉力τ0按初切应力图选取，见下图。

三．扭簧：
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径；
E---材料的弹性模量，一般不锈钢丝取188000Mpa ，碳素钢丝
取206000Mpa ；
D---弹簧外径；
ϕ---弹簧的扭转行程（角度）；
4. 应力： K1为曲度系数，顺旋向扭转取1，逆旋向扭转时按下式：
308τπ⋅=D d P 132
.10K d
M ⋅=σ
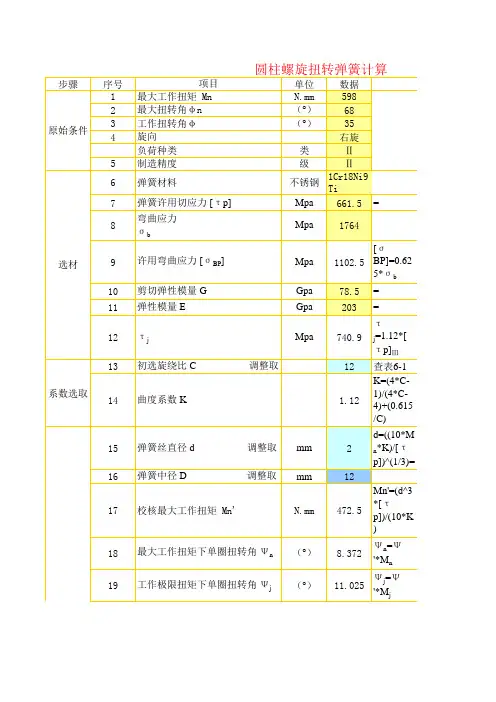
下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。

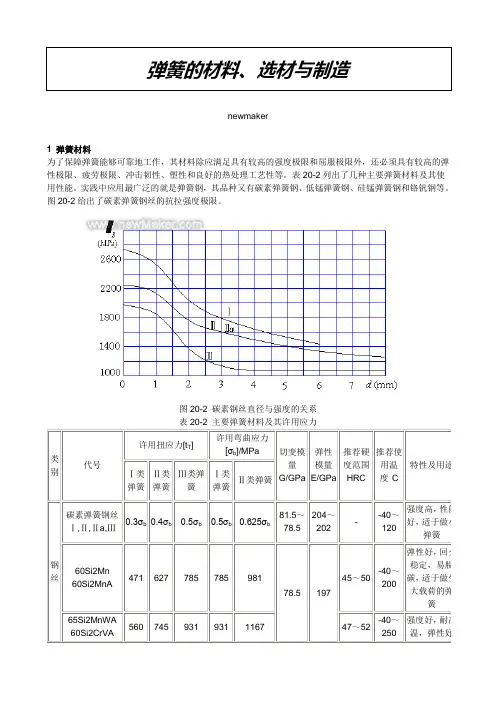
弹簧的材料、选材与制造newmaker1 弹簧材料为了保障弹簧能够可靠地工作，其材料除应满足具有较高的强度极限和屈服极限外，还必须具有较高的弹性极限、疲劳极限、冲击韧性、塑性和良好的热处理工艺性等。

表20-2列出了几种主要弹簧材料及其使用性能。

实践中应用最广泛的就是弹簧钢，其品种又有碳素弹簧钢、低锰弹簧钢、硅锰弹簧钢和铬钒钢等。

图20-2给出了碳素弹簧钢丝的抗拉强度极限。

图20-2 碳素钢丝直径与强度的关系表20-2 主要弹簧材料及其许用应力类别代号许用扭应力[t T]许用弯曲应力[σb]/MPa 切变模量G/GPa弹性模量E/GPa推荐硬度范围HRC推荐使用温度°C特性及用途Ⅰ类弹簧Ⅱ类弹簧Ⅲ类弹簧Ⅰ类弹簧Ⅱ类弹簧钢丝碳素弹簧钢丝Ⅰ,Ⅱ,Ⅱa,Ⅲ0.3σb0.4σb0.5σb0.5σb0.625σb81.5～78.5204～202--40～120强度高，性能好，适于做小弹簧60Si2Mn60Si2MnA471 627 785 785 98178.5 19745～50-40～200弹性好，回火稳定，易脱碳，适于做受大载荷的弹簧65Si2MnWA60Si2CrVA560 745 931 931 1167 47～52-40～250强度好，耐高温，弹性好注：1.按受力循环次数N不同，弹簧分为三类：Ⅰ类N>106；Ⅱ类N=103～105以及受冲击载荷的场合；Ⅲ类N<103。

2.碳素弹簧钢丝按机械性能不同分为Ⅰ、Ⅱ、Ⅱa、Ⅲ四组，Ⅰ组强度最高，依次为Ⅱ、Ⅱa、Ⅲ组。

3.弹簧的工作极限应力tlim：Ⅰ类￡1.67[t]；Ⅱ类￡1.25[t]；Ⅲ类￡1.12[t]。

4.轧制钢材的机械性能与钢丝相同。

5.碳素钢丝的切变模量和弹性模量对0.5～4mm直径有效，>4mm取下限。

2 材料选择弹簧材料选择必须充分考虑到弹簧的用途、重要程度与所受的载荷性质、大小、循环特性、工作温度、周围介质等使用条件，以及加工、热处理和经济性等因素，以便使选择结果与实际要求相吻合。

无色为输入值潜蓝色为输出值，自动生成项目输入值名称值材料线径mm d 1弹簧内径mm D 1 3.4弹簧外径mm D 25.4弹簧中径mm D 4.400D=D 1+d 材料弹性模量N/mm² E 186000旋绕比 C 4.40C=D/d 材料抗拉强度（应力）MPa σb 1850自由角度 º 0有效圈数 n2扭转刚度（N.mm/ º） M' 4.978最小负荷扭角º 3最小扭矩N.mm M 114.9最大负荷扭角º15最大扭矩N.mm M 274.7扭臂1长度 mm L 17最小弯曲应力MPa σmin 152.2扭壁2长度 mm L 26最大弯曲应力MPa σmax 761.0循环特征 γ0.20上限应力系数 σmax/σb 0.41σmax/σb最大负载状态下直径减少量 mm ΔD 0.09导杆直径 mm D'2.98a)、长扭臂弹簧二、疲劳度判断b）、短扭臂弹簧（L 1,L 2=0)公式判定说明：查下表疲劳度图，若γ与σmax/σb值的交点在图中 下方，说明该弹簧的疲劳强度N > 次，σmax/σb=0.7是弹簧不发生永久变形的极限值圆柱螺旋扭转弹簧疲劳度计算一、弹簧参数计算输入参数区域输出区域]}3/)([*3670/{'214L L Dn Ed M ++=ππ1φ2φ)/(3231min d M πσ=)/(3232max d M πσ=max min /σσγ=n10)360/(2n D D φ=∆)(9.0'1D D D ∆-=11'*φM M =22'*φM M =φ)]int([360n n -=φn 10。

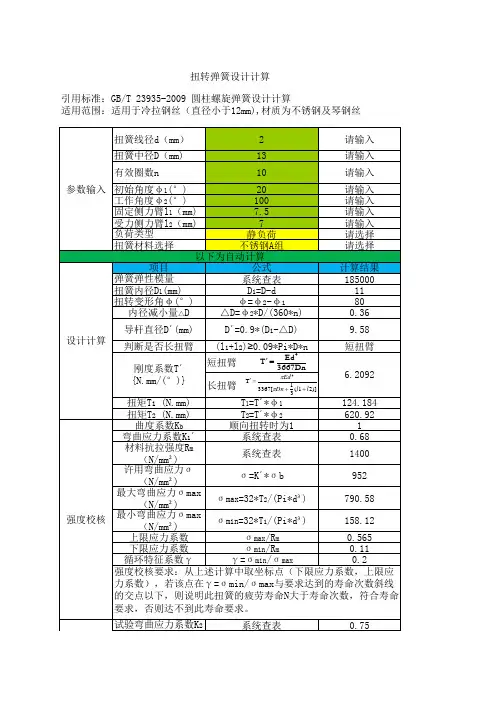
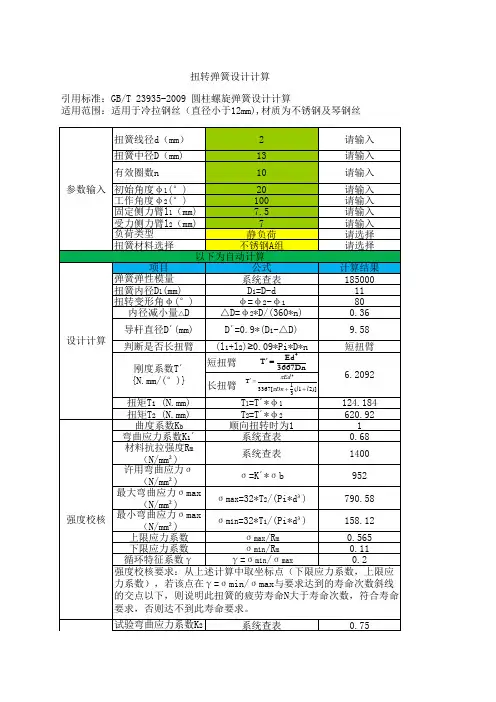
有效圈数是指弹簧能保持相同节距的圈数。

弹簧有效圈数的计算：总圈数—支撑圈，具体根据结构进行计算。

对于拉伸弹簧，有效圈数n＝总圈数n1，当n> 20时圆整为整数圈，当n<20时圆整为半圈。

对于压缩弹簧，有效圈数n为总圈数n1减去支撑圈数n2，n2可查表获得。

尾数应为1/4、1/2、3/4、或整圈，推荐1/2圈。

建议你查看GB 1973．1－89 《小型圆柱螺旋弹簧技术条件》中华人民共和国机械电子工业部1989－03－02批准1990－01－0 1实施小型圆柱螺旋弹簧技术条件GB 1973．1－89中华人民共和国机械电子工业部1989－03－02批准1990－01－01实施1 主题内容与适用范围木标准规定丁小型圆柱螺旋弹簧的技术要求、试验方法和检验规则。

本标准适用于圆截面圆柱螺旋压缩、拉伸和扭转弹簧(以下简称弹簧)。

弹簧材料的截面直径小于0．5 mm。

本标准不适用于特殊性能的弹簧。

2 引用标准GB 191 包装储运图示标志GB 1239．5 圆柱螺旋弹簧抽样检查GB 1805 弹簧术语GB 2828 逐批检查计数抽样程序及抽样表(适用于连续批的检查) GB 3123 硅青铜线GB 3124 锡青铜线GB 3134 铍青铜线GB 4357 碳素弹簧钢丝GB 4358 琴钢丝GB 4459．4 机械制图弹簧画法GB 4879 防锈包装GB 6543 瓦楞纸箱YB(T) 11 弹簧用不锈钢丝3 技术要求3．1 产品应符合本标准的要求，并按经规定程序批准的产品图样及技术文件制造。

3．2 极限偏差的等级弹簧特性与尺寸的极限偏差分为1、2、3三个等级。

各项目的等级应根据使用需要分别独立选定，并在图样上注明，未注明的则由制造厂从标准中选定。

3．3 压缩和拉伸弹簧的弹簧特性及其极限偏差3．3．1 弹簧特性压缩(或拉伸)弹簧的弹簧特性为指定高度(或长度)的负荷或刚度。

3．3．1．1 在指定高度(或长度)的负荷下，弹簧的变形量应在试验负荷时变形量的20％～80％之间。

扭簧的扭矩计算公式(一)扭簧的扭矩计算公式什么是扭簧的扭矩？扭簧是一种能够储存、释放扭转能量的弹簧，广泛应用于机械、汽车等领域。

其中，扭簧的扭矩是指扭簧在扭动时产生的力矩，也称为弹矩。

扭簧的扭矩计算公式扭簧的扭矩计算公式可以根据扭簧的结构和材料来确定。

以下是一些常见的扭簧的扭矩计算公式：1.一般弹簧材料扭矩计算公式：T=k⋅θ公式中，T表示扭矩，k表示弹簧的弹性系数，θ表示扭转角度。

示例说明：假设有一根弹簧，其弹性系数为 2 Nm/deg，扭转角度为45°，则根据公式可计算出扭矩为 90 Nm。

2.圆柱螺旋弹簧的扭矩计算公式：T=G⋅d 432⋅D⋅θ公式中，T表示扭矩，G表示剪切模量，d表示线径，D表示弹簧的平均直径，θ表示扭转角度。

示例说明：假设有一根圆柱螺旋弹簧，其剪切模量为 80 GPa，线径为 10 mm，平均直径为 100 mm，扭转角度为90°，则根据公式可计算出扭矩为 Nm。

3.方柱螺旋弹簧的扭矩计算公式：T=G⋅b 3⋅ℎ16⋅D⋅θ公式中，T表示扭矩，G表示剪切模量，b表示方柱螺旋弹簧的边长，ℎ表示方柱螺旋弹簧的高度，D表示弹簧的平均直径，θ表示扭转角度。

示例说明：假设有一根方柱螺旋弹簧，其剪切模量为 60 GPa，边长为 20 mm，高度为 30 mm，平均直径为 150 mm，扭转角度为180°，则根据公式可计算出扭矩为 Nm。

结论扭簧的扭矩计算公式根据扭簧的结构和材料的不同而有所区别。

通过选择合适的计算公式，可以准确计算出扭簧在扭动时产生的扭矩。