用表格表示两个变量之间的关系(导学案)

《用表格表示的变量间关系》教案第一章：引言1.1 教学目标让学生理解变量间关系的概念。

让学生掌握用表格表示变量间关系的方法。

1.2 教学内容介绍变量间关系的概念。

解释用表格表示变量间关系的原因和重要性。

1.3 教学方法通过实例引导学生理解变量间关系。

使用图表和实际数据展示变量间的关系。

1.4 教学评估观察学生在课堂上的参与程度和理解程度。

通过提问和讨论检查学生对变量间关系的理解。

第二章：单变量数据的表格表示2.1 教学目标让学生掌握单变量数据的表格表示方法。

让学生能够从表格中提取和理解信息。

2.2 教学内容介绍单变量数据的表格表示方法，包括频数表、频率表和交叉表。

解释如何从表格中提取和理解信息。

2.3 教学方法通过实例演示单变量数据的表格表示方法。

引导学生从表格中提取和理解信息。

2.4 教学评估观察学生在课堂上的参与程度和理解程度。

通过提问和讨论检查学生对单变量数据的表格表示方法的理解。

第三章：双变量数据的表格表示3.1 教学目标让学生掌握双变量数据的表格表示方法。

让学生能够从表格中提取和理解信息。

3.2 教学内容介绍双变量数据的表格表示方法，包括列联表和交叉表。

解释如何从表格中提取和理解信息。

3.3 教学方法通过实例演示双变量数据的表格表示方法。

引导学生从表格中提取和理解信息。

3.4 教学评估观察学生在课堂上的参与程度和理解程度。

通过提问和讨论检查学生对双变量数据的表格表示方法的理解。

第四章：表格表示的变量间关系的应用4.1 教学目标让学生能够应用表格表示的变量间关系解决实际问题。

让学生能够解释和分析表格表示的变量间关系。

4.2 教学内容介绍如何应用表格表示的变量间关系解决实际问题。

解释如何解释和分析表格表示的变量间关系。

4.3 教学方法通过实例引导学生应用表格表示的变量间关系解决实际问题。

引导学生解释和分析表格表示的变量间关系。

4.4 教学评估观察学生在课堂上的参与程度和理解程度。

通过提问和讨论检查学生对应用表格表示的变量间关系的理解。

学 案 课 题 3.3.1用图像表示两个变量之间的关系 设 计 人 贺建鹏

使用人 序号 授课时间

学 习 目 标

1、了解两个变量之间的对应关系，初步形成函数的思想。 2、结合具体情境理解图象上的点所表示的意义。 3、发展从图象中获得信息的能力及有条理地进行语言表达的能力。 4、理解用数学的方法描述变量之间的关系，感受数学的价值。 一、合作学习 下表是成都市某天各时刻的气温值，请分析这天的气温变化情况．（要求直观、形象、生动） 时刻 0 3 6 9 12 15 18 21 24 温度 26 23 24 27 31 37 35 31 26

小明根据上表用Excel绘制的一张气温变化曲线图，直观形象地表达了温度随时间的变化而变化的情况，你能根据下图回答下列问题吗？ （1）上午9时的温度是多少？12时呢？ （2）这一天的最高温度是多少？是在几时达到的？最低温度呢？ （3）这一天的温差是多少？从最低温度到最高温度经过了多少时间？ （4）在什么时间范围内温度在上升？在什么时间范围内温度在下降？ （5）图中的A点表示的是什么？B点呢？

小结：图像是我们表示变量之间关系的又一种方法，它的特点是非常直观。在用图像表示变量之间的关系时，通常用 上的点表示自变量，用 上的点表示因变量。 议一议： 1、一天中，骆驼体温的变化范围是什么？它的体温从最低上升到最高需要多少时间？ 2、从16时到24时，骆驼的体温下降了多少？ 3、在什么时间范围内骆驼的体温在上升？在什么时间范围内骆驼的体温在下降？ 4、你能看出第二天8时骆驼的体温与第一天8时有什么关系吗？其他时刻呢？ 5、A点表示的是什么？还有几时的温度与A点所表示的温度相同？ 6、你还知道哪些关于骆驼的趣事？

二、目标检测： 1、某市一周平均气温(℃)如图1所示下列说法不正确的是( ) A、星期二的平均气温最高 B、星期四到星期日天气逐渐转暖 C、这一周最高气温与最低气温相差4℃ D、星期四的平均气温最低

1 用表格表示两个变量的关系项目内容1.幼儿园大班有30人,小班有20人,老师要把140个橘子分到两个班,怎么分合理?2.读教材第18页例题。

分析与解答:(1)已知8:00时汽车里程表显示的读数是( )千米,9:00时显示的读数是( )千米,则汽车1小时行驶的路程( )千米即为汽车的速度。

(2)已知汽车的速度,则汽车行驶的时间( ),行驶的路程( )。

表格应分别填入( )、( )。

(3)通过观察可以发现,当速度一定时,相对应的路程与时间的比值是相等的。

3.通过预习,我知道了在速度一定时,行驶的路程会随着时间的增长而( )。

4.下表是不同年龄儿童每分钟呼吸次数统计表。

年龄新生儿1岁3岁7岁14岁呼吸次数(次)42 30 24 22 20(1)上表中哪些量在发生变化?(2)说一说:儿童14岁前每分钟呼吸次数是如何随年龄增长而变化的?温馨知识准备:仔细观察,找出联系。

提示答案：1.30∶20=3∶23+2=5140×=84(个)140×=56(个)大班分84个,小班分56个2.(1)8724 8814 90(2)越长越多450 540 (3)略3.增加4.(1)年龄每分钟呼吸次数(2)每分钟呼吸次数随年龄的增长而减少2 认识成正比例关系的量项内容目1.每袋面粉的质量一定,面粉的总质量和袋数之间是什么关系?2.读教材第19页例题。

分析与解答:从表中可以发现:买笔的数量越多,总价( )。

总价与数量是两种( ),它们与单价的关系:( )。

已知单价一定,就是总价与数量的( )一定,所以总价与数量成( )比例。

3.两种( )的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。

4.购买礼品的份数和总价如下表。

份数10 20 30 40 50总价80 160 240 320 400(元)(1)写出总价与份数的比。

(2)说明这个比值所表示的意义。

第四章变量之间的关系§4．1 用表格表示的变量关系年级：七年级班级：学生姓名：制作人：李兴林一、学习目标：（1分钟）1、知道变量、因变量、自变量和常量的概念；2、能从表格中获得变量之间的关系的信息；3、会用表格表示变量之间的关系。

二、自主探究：（10分钟）（一）、预习教材P96~P97（二）、思考：什么是变量？什么是自变量？什么是因变量？（三）、预习作业：1（1（2）根据表中的数据，你认为老师在第____分钟提出观念比较适宜？说出你的理由．三、学习引导：（15分钟）（一）要点引导：（2分钟）1、在一个变化过程中数值保持不变的量叫做______可以取不同数值的量叫做______，如果一个量随着另外一个量的变化而变化，那么把这个量叫做______，另一个量叫做______．2、本节是通过______形式来表示两个变量之间的关系的．（1）支撑物高度为70厘米时，小车下滑时间是多少？（2）如果用h表示支撑物高度，t表示小车下滑时间，随着h逐渐变大，t的变化趋势是什么？（3）h每增加10厘米，t的变化情况相同吗？（4）估计当h=110时，t的值是多少，你是怎样估计的？（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）如果用t表示时间，v表示速度，那么随着t的变化，v的变化趋势是什么？（3）当t每增加1秒时，v的变化情况相同吗？在哪1秒钟内，v的增加最大？（4）若高速公路上小汽车行驶速度的上限为120千米/时，试估计大约还需几秒这辆小汽车速度就将达到这个上限？2、下表是明明商行某商品的销售情况，该商品原价为560元，随着不同幅度的降价（单位：元），日销量（1）上表反映了哪两个变量之间的关系？其中那个是自变量，哪个是因变量？（2）每降价5元，日销量增加多少件？请你估计降价之前的日销量是多少？（3）如果售价为500元时，日销量为多少？四、小组合作学习：（18分钟）1、完成教材第97页随堂练习：（5分钟）2、完成教材第97-99页习题：（13分钟）五、回顾小结：（2分钟）§4．2 用关系式表示的变量间的关系班级： 学生姓名： 制作人：李兴林1、探索某些图形中变量之间的关系的过程，进一步体会一个变量对另一个变量的影响，发展符号感；2、能根据具体情景，用关系式表示某些变量之间的关系。

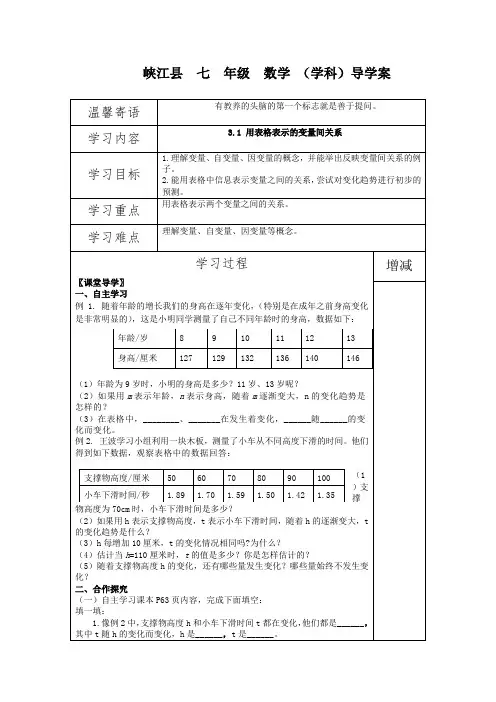
峡江县 七 年级 数学 （学科）导学案温馨寄语 有教养的头脑的第一个标志就是善于提问。

学习内容 3.1 用表格表示的变量间关系学习目标 1.理解变量、自变量、因变量的概念，并能举出反映变量间关系的例子。

2.能用表格中信息表示变量之间的关系，尝试对变化趋势进行初步的预测。

学习重点 用表格表示两个变量之间的关系。

学习难点理解变量、自变量、因变量等概念。

学习过程〖课堂导学〗一、自主学习例1. 随着年龄的增长我们的身高在逐年变化，（特别是在成年之前身高变化是非常明显的），这是小明同学测量了自己不同年龄时的身高，数据如下：（1）年龄为9岁时，小明的身高是多少？11岁、13岁呢？（2）如果用m 表示年龄，n 表示身高，随着m 逐渐变大，n 的变化趋势是怎样的？（3）在表格中，________、_______在发生着变化，______随______的变化而变化。

例2. 王波学习小组利用一块木板，测量了小车从不同高度下滑的时间。

他们得到如下数据，观察表格中的数据回答：（1）支撑物高度为70cm 时，小车下滑时间是多少？（2）如果用h 表示支撑物高度，t 表示小车下滑时间，随着h 的逐渐变大，t 的变化趋势是什么？（3）h 每增加10厘米，t 的变化情况相同吗?为什么？（4）估计当h =110厘米时，t 的值是多少？你是怎样估计的？（5）随着支撑物高度h 的变化，还有哪些量发生变化？哪些量始终不发生变化？二、合作探究（一）自主学习课本P63页内容，完成下面填空：填一填：1.像例2中，支撑物高度h 和小车下滑时间t 都在变化，他们都是______，其中t 随h 的变化而变化，h 是______，t 是______。

年龄/岁 8 9 10 11 12 13 身高/厘米 127 129 132 136 140 146 支撑物高度/厘米 50 60 70 80 90 100 小车下滑时间/秒 1.89 1.70 1.59 1.50 1.42 1.35 增减2.在这一变化过程中，小车下滑的距离（木板长度）一直没有变化。

用表格表示变量之间的关系教案一、教学目标：1. 让学生理解什么是变量，并能够识别和描述日常生活中的变量。

2. 让学生掌握用表格表示变量之间的关系的方法。

3. 培养学生收集、整理、分析数据的能力，提高学生的逻辑思维能力。

二、教学内容：1. 变量概念的引入：介绍变量的定义，让学生举例说明生活中的变量。

2. 表格表示变量之间的关系：讲解如何用表格表示变量之间的关系，包括列表示和行表示。

3. 实践操作：学生分组讨论，选取生活中的实例，用表格表示变量之间的关系。

三、教学重点与难点：重点：用表格表示变量之间的关系的方法。

难点：如何准确地收集和整理数据，并用表格表示出来。

四、教学方法：1. 讲授法：讲解变量的定义和表格表示变量之间的关系的方法。

2. 案例分析法：分析生活中的实例，让学生理解变量之间的关系。

3. 实践操作法：学生分组讨论，选取实例，动手操作，用表格表示变量之间的关系。

五、教学准备：1. 教学PPT：包含变量的定义、表格表示变量之间的关系的方法及实例。

2. 练习题：提供一些生活中的实例，让学生课后练习用表格表示变量之间的关系。

3. 分组讨论的道具：如纸张、笔等，供学生分组讨论时使用。

六、教学过程：1. 导入新课：通过一个简单的例子引入变量和表格表示变量之间的关系。

2. 讲解变量：讲解变量的定义，让学生举例说明生活中的变量。

3. 讲解表格表示变量之间的关系：讲解如何用表格表示变量之间的关系，包括列表示和行表示。

4. 实践操作：学生分组讨论，选取生活中的实例，用表格表示变量之间的关系。

5. 案例分析：分析一些实际的案例，让学生理解变量之间的关系。

6. 总结与复习：对本节课的内容进行总结，让学生复习所学的知识。

七、课堂练习：1. 让学生独立完成练习题，用表格表示给定的变量之间的关系。

2. 让学生分组讨论，互相检查答案，并解释自己的解题思路。

八、课堂小结：1. 对本节课的内容进行总结，让学生回顾所学的知识点。

变量间的相关关系、回归分析导学案学习目标：1.会作两个相关变量的数据的散点图，会利用散点图认识变量的相关关系；了解最小二乘法的思想，能根据给出的系数公式建立线性回归方程；2.了解回归分析的基本思想、方法及其简单应用.学习重点：了解回归模型与函数模型的区别；了解任何模型只能近似描述实际问题；模型拟合效果的分析工具：残差分析和指标2R .学习难点：残差变量的解释与分析；指标2R 的理解.知识梳理1. 变量间的相关关系 （1）两个变量之间的关系包括 和 ，相关关系是指 （2）散点图是指 ，观察散点图可知，相关关系又包括 和 。

（3）线性相关关系及回归直线： 2.回归分析的基本思想及其初步应用 （1）对具有 的两个变量进行统计分析的方法叫 。

回归分析的一般步骤为： （2）回归直线方程：设所求的直线方程为y bx a ∧=+，其中121()(),()niii nii x x y y b a y bx x x ==--==--∑∑，1111,,nni i i i x x y y n n ====∑∑ 称为样本点的中心，回归直线过 ，回归方程的截距a 和斜率b 是用 计算出来的，最小二乘法是指（3）回归分析：如何检查所建立的回归模型拟合效果的好坏？(4)相关系数①12211()()()()niii n niii i x x y y r x x y y ===--=--∑∑∑②当0r >时,表明两个变量正相关；当0r <时,表明两个变量负相关.r 的绝对值越接近于0时,表明两个变量之间几乎不存在线性相关关系.通常||r 大于0.75时,认为两个变量有很强的线性相关性. 3.残差分析(1)总偏差平方和：把每个效应(观测值减去总的平均值)的平方加起来即:∑=-ni iy y12)((2)残差：数据点和它回归直线上相应位置的差异)ˆi i yy -（是随机误差的效应,称i i i y y e ˆˆ-=为残差. (3)残差平方和∑=-ni i iyy12)ˆ(.(4)相关指数∑∑==--=ni ini i iy yyyR 12122)()ˆ(2R 的值越大,说明残差平方和越小,也就是说模型的拟合效果越好.在线性回归模型中, 2R 表示解释变量对预报变量变化的贡献率, 2R 越接近于1,表示回归的效果越好.4.建立回归模型的步骤 (1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量. (2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系(如是否存在线性关系等).(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y bx a =+).应用：1.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y( x 3 4 5 6 y2.5344.5(1) (2)请根据上表提供的数据，用最小二乘法求出Y 关于x 的线性回归方程Y=bx+a ；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值：3×2.5+4×3+5×4+6×4.5=66.5)2.测得某国10对父子身高(单位:英寸)如下:(1)对变量y x 与进行相关性检验;(2)如果y x 与之间具有线性相关关系,求回归方程. (3)如果父亲的身高为73英寸,估计儿子的身高.(二)非线性回归分析1.非线性回归模型:当回归方程不是形如y bx a =+时称之为非线性回归模型.2.非线性回归模型的拟合效果:对于给定的样本点1122(,),(,),,(,)n n x y x y x y ,两个含有未知数的模型(1)(2)(,)(,)y f x a y g x b ==和,其中a b 和都是未知参数. 可按如下的步骤比较它们的拟合效果:(1)分别建立对应于两个模型的回归方程(1)(2)ˆˆˆˆ(,)(,)y f x a y g x b ==和,其中ˆˆa b 和分别是参数a b 和的估计值;(2)分别计算两个回归方程的残差平方和(1)(1)2(2)(2)211ˆˆˆˆ()()nni i i i i i Qy yQ y y===-=-∑∑和;(3)若(1)ˆQ ＜(2)ˆQ ,则(1)(2)ˆˆˆˆ(,)(,)y f x a y g x b ==的效果比;反之, (1)(2)ˆˆˆˆ(,)(,)y f x a y g x b ==的效果不如的好.: 天数x/天 1 2 3 4 5 6 繁殖个数y/个612254995190(1)用天数x 作解释变量,繁殖个数y 作预报变量,作出这些数据的散点图; (2)描述解释变量x 与预报变量y 之间的关系; (3)计算残差平方和、相关指数.。