数码相机定位方法探究(史奎举)
- 格式:pdf
- 大小:189.89 KB
- 文档页数:11

分析数码相机定位原理及其相关问题
了解数码相机定位原理,可以加深我们对这种产品的熟悉,用法起来越发得心应手。
特殊是从事这方面研制和开发的工程师,这些都是基础。
本文主要是分析数码相机定位原理,主要是深化分析它的标定的方式、定位的办法,如何利用电子实现光学影像和电子数据之间的转换。
数码相机工作原理
光芒通过镜头或者镜头组进入相机,通过成像元件(即CCD/传感芯片)按照光芒的不同转化为数字信号,数字信号通过影像运算芯片储存在存储设备中,也就是我们常说了相机自身的存储卡或者内存卡中。
它集成了影像信息的转换、存储和传输等部件,具有数字化存取模式,与电脑交互处理和实时拍摄等特点(数码相机成像原理)。
我们可以通过相机的屏幕也可以观察照片或者已经录制好的视频,也可以通过数据线(普通是)或者内存卡和电脑衔接,将数据或者视频数据传输到个人PC机上扫瞄。
数码相机定位原理
指用数码相机摄制物体的相片确定物体表面某些特征点的位置,通过定位,可以让图像越发清楚,和我们肉眼看到的影像对照显得越发真切可信。
在摄影测量学中有以下四个标定问题: 这些标定问题主要起源于高空摄影技术,是摄影测量中的经典问题.
(1)肯定定位:通过标定点确定两个坐标系在肯定坐标系统中的变换关系,或确定测距传感器在肯定坐标系中的位置和方向.
(2)相对定位:通过场景中的标定点投影确定两个摄象机之间的相对位置和方向.
(3)外部定位:通过场景中的标定点投影确定摄象机在肯定坐标系中的位置和方向.
(4)内部定位:确定摄象机内部几何参数,包括摄象机常数,主点的位置以及透镜变形的修正量.
第1页共2页。

数码相机标定方法研究数码相机标定方法是一种经过精确测量和计算的过程,用于确定相机的内部参数和外部参数,以提高图像处理的精度和准确性。
相机标定方法不仅应用于计算机视觉领域,还广泛应用于机器人导航、虚拟现实等领域。
本文将着重介绍数码相机标定方法的研究。
数码相机标定方法的研究可以分为两个主要方面:内部参数标定和外部参数标定。
内部参数主要包括焦距、主点坐标、畸变系数等,它们是相机的固有特性;外部参数包括相机的位置和姿态,即相机与被摄物体的相对位置关系。
内部参数标定通常使用棋盘格标定方法。
该方法简单易行,只需在相机前放置一个已知尺寸的棋盘格,通过对棋盘在图像中的检测和计算,可以准确地估计出相机的内部参数。
具体步骤如下:首先,拍摄一系列棋盘格图像,要求棋盘格在不同的位置和角度下都能被完整地看到;然后,利用图像处理技术检测棋盘格角点的位置;最后,利用非线性最小二乘法对参数进行估计。
这种方法的优点是简单易行,不需要复杂的设备和专业知识。
缺点是对于较大的畸变程度和复杂的相机模型,精度会有所降低。
外部参数标定通常使用三维点和对应的图像点进行计算。
这种方法需要之前进行三维重建,并使用三维点云和图像点进行匹配。
通过对匹配点进行三维坐标的计算,结合相机坐标系与世界坐标系之间的映射关系,可以准确地估计出相机的外部参数。
具体步骤如下:首先,进行三维重建,获取一系列三维点;然后,通过计算图像点与三维点之间的对应关系,求解相机的外部参数;最后,利用非线性最小二乘法对参数进行优化。
这种方法的优点是精度高,适用于复杂场景和大视场的情况。
缺点是对于简单场景和小视场的情况,计算量较大。
除了以上两种常见的标定方法,还有其他一些方法被用于数码相机的标定研究。
例如,基于光线追踪的方法可以模拟相机成像过程,通过优化来估计相机的内部参数和外部参数;基于深度学习的方法可以通过神经网络来学习相机的内部参数和外部参数。
这些方法在特定的应用场景下具有较好的效果,但也有一定的局限性。

数码相机定位模型分析摘 要在交通监管中,要定位物体上一个特征点,需用两部固定于不同位置的相机拍摄得到物体的像,分别获得在两部相机平面上的坐标。
只要知道两部相机的精确的相对位置,就可以用几何的方法得到该特征点在固定一部相机的坐标系中的坐标,也就确定了特征点的位置。
所以,进行数码相机的标定就是一项非常重要的工作,本文针对数码相机的标定问题,进行以下的研究工作。
1、根据数码相机成像原理,结合数字摄影测量学的有关内容,分别建立物方坐标系、图像坐标系、光心坐标系和辅助坐标系,定义拍摄照片的内、外方位元素,利用像点的空间直角坐标变换与中心投影构像方程,结合单像空间后方交会的有关概念,列出空间后方交会的误差方程式与法方程式,建立空间图像坐标的解算模型。
2、根据照片的像素以及各标志点所处的位置,利用基于几何特性的椭圆中心像坐标的快速求取方法,初步定出各标志点的中心图像坐标。
在建立的物方坐标系内,读出特征点的实际坐标,将相关数据引入前述模型中,采用非线性最小二乘法进行求解。
经11次迭代,求算的各点图像坐标为(单位:mm ): (18.7685,19.1054A A x y =−=)(8.5091,B x =−18.0789B y =)(12.3984,C x = 16.1065C y =)( 6.6438,11.1209D D x y ==−)(21.8276,11.6190E E x y =−=−)3、针对模型的精度问题,利用三点共线原理,将光心、特征点的坐标转换至物方坐标系内,并分别计算光心与各特征点连线在物方坐标系)(xoy 平面内的投影,反推各特征点的解算坐标,以解算坐标及实际坐标求算点误差距离,以误差距离平均值作为精度的评判指标,设计出精度评判方法。
引入一般数学问题不定性分析方法,结合各标志点初始图像坐标的变化对求解结果的影响,分析该算法的稳定性,得出在特定靶位的条件下,算法基本上能够保证稳定的结论。
4、建立光心坐标系与物方坐标系的的转换模型,求解两部相机光心坐标在物方坐标系内坐标,并利用三点共面原理建立确定两部相机相对位置的具体方法,从坐标及像平面夹角等几个方面给出相对位置的表达式。
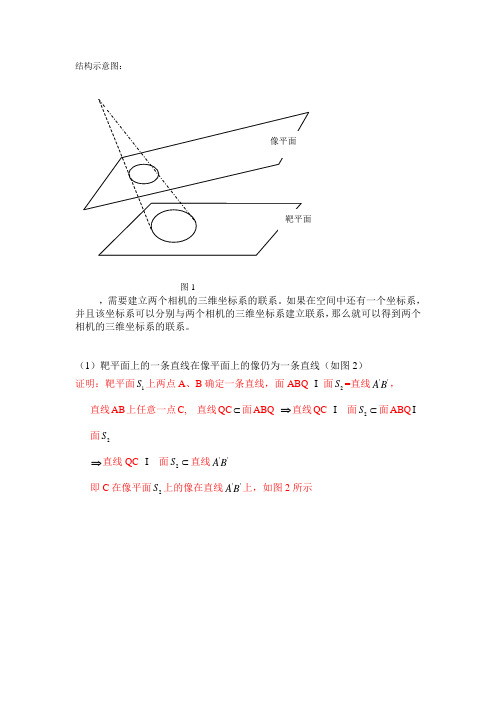
结构示意图:图1,需要建立两个相机的三维坐标系的联系。
如果在空间中还有一个坐标系,并且该坐标系可以分别与两个相机的三维坐标系建立联系,那么就可以得到两个相机的三维坐标系的联系。
(1)靶平面上的一条直线在像平面上的像仍为一条直线(如图2) 证明:靶平面1S 上两点A 、B 确定一条直线,面ABQ 面2S =直线''A B , 直线AB 上任意一点C, 直线QC ⊂面ABQ ⇒直线QC 面2S ⊂面ABQ 面2S⇒直线QC 面2S ⊂直线''A B即C 在像平面2S 上的像在直线''A B 上,如图2所示图2(2)如果靶平面上的直线1l 和2l 交于O 点,那么在像平面上,1l 、 2l 的像'1l 、'2l 交于 'O 点, 'O 为 O 的像。
(如图3) 证明:直线1l 和2l 交于O 点⇒O ∈1l1l 的像为'1l ,'O 为 O 的像,由定理1,得到'O ∈ '1l 同理'O ∈'2l因此'O∈'1l '2l即'1l 、 '2l 交于 'O ,如图3所示:图3(3)如果靶平面上直线l 和圆O 相切于A 点,那么在像平面上, l 和圆O 的像'l 、 圆'O 切于'A 点,'A 为A 的像。
(如图4) 证明:A ∈圆O, A ∈l⇒ 'A ∈圆'O ,'A ∈'l因此'A 为圆'O 和直线'l 的公共点假设圆'O 和直线'l 另有一公共点'B ,'B 在面1S 中的像为B同理可得B 为圆O 和直线l的公共点,即B 与A 重合那么'A , 'B 在面1S 中的像为A, 与“靶平面上的点与像平面上的点一一对应”矛盾,因此圆'O 和直线'l 仅有一公共点'A因此,直线'l 、 圆'O 切于'A 点,如图4所示:图4(4)如果靶平面上直线 1l 、 2l 为圆1O 圆 2O 的内公切线,直线 1l 、 2l 交于A ,那么在像平面上, '1l 、'2l 为圆'1O 、圆'2O 的内公切线, A 在像平面上的像 'A 为'1l 、'2l 的交点,且 'A 、'1O 、'2O 共线。


数码相机定位问题的研究摘要本文从计算机视觉系统出发,对数码相机的定位问题进行了深入研究,并建立了相应的数学模型。
对于问题一,先运用光学成像的相关知识,建立了针孔模型,然后又考虑了摄像机的畸变问题,对上述模型进行改进,建立了非线性模型,并给出了相应的算法。
对于问题二,基于问题一中建立的模型,运用最小二乘法的思想,利用Matlab软件进行了检验,并对该方法的精度和稳定性进行了讨论。
对于问题四,运用几何学的相关知识,建立了双目定位系统中两部相机之间的关系式,从而确定了它们在空间中的相对位置关系,并给出了相应的算法。
本文综合考虑多方面因素,公式、表格、图形表达相结合,建立的模型结构严密,具有较强的逻辑推理性,最后并对结果进行分析与检验,符合实际情况,具有一定的参考价值。
关键词:数码相机针孔模型靶标蒙特卡罗一、问题重述1.1基本情况数码相机定位在交通监管(电子警察)等方面有广泛的应用。
所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。
最常用的定位方法是双目定位,即用两部相机来定位。
对物体上一个特征点,用两部固定于不同位置的相机摄得物体的像,分别获得该点在两部相机像平面上的坐标。
只要知道两部相机精确的相对位置,就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标,即确定了特征点的位置。
于是对双目定位,精确地确定两部相机的相对位置就是关键,这一过程称为系统标定。
标定的一种做法是:在一块平板上画若干个点,同时用这两部相机照相,分别得到这些点在它们像平面上的像点,利用这两组像点的几何关系就可以得到这两部相机的相对位置。
然而,无论在物平面或像平面上都无法直接得到没有几何尺寸的“点”。
实际的做法是在物平面上画若干个圆(称为靶标),它们的圆心就是几何的点了。
而它们的像一般会变形,如附件图1所示,所以必须从靶标上的这些圆的像中把圆心的像精确地找到,标定就可实现。
有人设计靶标如下,取1个边长为100mm的正方形,分别以四个顶点(对应为A、C、D、E)为圆心,12mm为半径作圆。
数码相机强大的对焦锁定和对焦定位技术数码相机强大的对焦锁定和对焦定位技术1、什么是对焦?先讲一下什么是对焦吧。
简单理解下,对——对准,焦——焦点(拍摄目标),合起来就是对准焦点,而这里还不单单就是这个意思,整体的意思就是看清楚对准的焦点。
可以这样简单的理解为:相机在拍摄时必须看清楚拍摄的目标,只有在看清楚拍摄目标的情况下,才能拍摄出清晰完整的照片。
好了,知道对焦的重要性了,就要注意这点,拍摄时一定要对焦,那怎么使用对焦?怎么确定对没对焦呢?大家拍摄的时候都发现屏幕上会有个白色的框框吧,那个就是拿来对焦的,拍摄的时候轻微按下快门键,切记别按到底,否则就已经拍摄了。
手固定住,你会发现白色的框框变成绿色的了,这时,你已经成功对焦了,但还要注意:绿色框出现时也并非百分百对上焦了,要确定是否真正对上焦,还要看屏幕显示的画面是否清晰,如果模糊哪怕显示是绿框,那还是对焦失败。
在什么情况下会对焦失败呢?答:其实相机就跟人一个样,在过于靠近拍摄物体和光线过强或过弱的时候,人在这种情况下看东西也绝对不会清楚,比如你把眼睛靠近要看的东西10厘米左右,你会发现越靠近要看的东西就会越模糊,还有些人会奇怪为什么焦对上了,而对焦框以外的景物会比较模糊呢?还是跟人一样,比如你把一个景物很清楚的时候,周围的背景绝对也会模糊吧。
那怎么判断对焦失败呢?当白色的框框变成红色就是对焦失败了,明白对焦了吧?2、什么是对焦锁定?有什么作用?好了,讲我的重大发现,对焦锁定,对焦锁定的使用前提就是先对焦,对焦的同时也就锁定了,那对焦锁定是什么意思?怎么运用这个技术呢?简单理解下,对焦——对焦后的拍摄目标,锁定——锁定,合起来就是锁定对焦后的拍摄目标。
要注意,这里不是这个意思,这里的锁定不是锁定对焦后的拍摄目标而是锁定对焦后的拍摄目标与相机之间的距离,而这段被锁定的距离就是相机能对焦的有效距离,使用这段距离拍摄任何一个目标都可以实现对焦。
比如在拍离相机20厘米左右的微距景物,对焦后,保持对焦状态,便可以随便移动其他景物来拍摄,但必须保持20厘米左右的距离,否则拍摄出来的景物就因没对上焦而模糊。
基于两步法的数码相机定位摘要数码相机定位在机器自动装配系统、工业视觉检测与识别、三维重建、机器人视觉导航、运动分析、海上目标跟踪、交通监管(电子警察)等诸多领域中得到了运用。
本文给出了确定靶标上圆的圆心在该相机像平面的像坐标的数学模型及确定两部固定相机相对位置的数学模型,并设计出了相应的求解算法。
首先在仅考虑单相机的情况下,在分析相机成像原理和四个坐标系之间的相互变换关系的基础上,考虑了相机径向畸变和切向畸变即非线性畸变因素,选择了一种简化模型,克服了相机内外参数未知情况下求解像坐标的困难,最终建立了基于两步法的像坐标确定模型。
该模型满足牛顿迭代法的收敛条件,保证了模型解的稳定性。
其次利用该模型,针对问题1和问题2,借助于Matlab工具,计算了靶标上给定5个圆的圆心像坐标。
然后选择Canny算子对给定靶标的像的几何中心进行了精确检测,并对两种结果进行了对比,分析了误差,精度及稳定性。
比较结果如表1所示:U坐标的平均误差:1.6551,V坐标的平均误差:1.6754 平均误差:1.6653最大误差点为C点,最小误差点为A点。
根据表1的数据证明了两步法确定像坐标的模型具有一定的可靠性和实用性。
然后根据给定靶标模型,并在上述模型的基础之上建立了确定两部相机相对位置的模型,同时给出基于平行线“消隐点”理论的切实可行的解法。
本文最后讨论了文中所建模型和所给算法的优缺点及改进方向。
关键词:两步法;像坐标;内外参数;边缘检测;相对位置;平行线消隐点一、问题的提出1.1 背景说明数码相机定位在交通监管(电子警察)等方面有广泛的应用。
由于目前数字图像的处理速度越来越快,且可达0.02个像素精度[1],因此考虑畸变系统误差的高精度标定具有重要的意义。
所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。
最常用的定位方法是双目定位,即用两部相机来定位。
对物体上一个特征点,用两部固定于不同位置的相机摄得物体的像,分别获得该点在两部相机像平面上的坐标。
数码相机定位的数学模型摘要随着数码相机定位在各领域的广泛应用,对相关问题《机器视觉》的研究也成为热点。
因此建立一个精度较高,稳定性好的数码相机定位的数学模型,具有很好的现实意义。
问题1要求给出确定靶标上圆的圆心在给定相机像平面的像坐标的算法,问题2利用问题1的模型对给定数据求解。
为此,首先建立了四个空间直角坐标系,在MATLAB中把图3的数字信息提取出来,主要是五个椭圆的边缘点的信息;同时为了便于运算,通过坐标变换将计算机图像坐标变换为图像坐标;并用提取的图像边界坐标拟合出5个椭圆的方程,利用“曲线切线的投影仍与曲线的投影相切,而且切点的投影仍为投影的切点”这一引理,提取出靶标上圆及其像上的公切点的坐标作为特征点,利用RAC两步法标定过程和最小二乘法建立了计算世界坐标系到相机坐标系的旋转变换矩阵R和平移向量T及径向畸变系数k的算法。
利用16个公切点作为特征点,通过Matalb编程求得靶标上圆的圆心在文中给定相机像平面的五个坐标(单位:mm):A(-49.7132, 51.1289 417.1958),B(-23.3475, 49.1539 417.1958),C(33.8194, 44.8716, 417.1958),D(18.8173,-31.5798, 417.1958),E(-59.7830, -31.1754, 417.1958)。
问题3的解决分为两步:一是通过对模型计算出的焦距及畸变系数及上面五个坐标值的分析得出模型的精度较高的结论;二是采用改变特征点数的方法或利用“A,B,C三个标靶的中心的像应在一条直线上”验证模型的稳定性。
问题4采用二目立体视觉模型确定了给出两部固定相机相对位置的数学模型和方法。
本文建立的算法可操作性强,精度较高,稳定性好,对解决类似问题的计算有一定的推广价值。
关键词:拟合椭圆特征点提取RAC两步法坐标旋转矩阵公切点数码相机定位的数学模型一问题的提出数码相机定位的数学模型来源于2008年全国大学生数学建模竞赛的A题。
数码相机相对位置定位方法1.摘要本文给出了空间中两部固定照相机相对位置的标定方法,将照相机成像过程近似为针孔成像过程,使得成像过程中光学中心—像点—物点三点共线,实现了成像的非线性到线性的简化。
文中将标定两部相机相对位置的方法分成三个步骤:第一步,将针孔成像抽象为点投影式映射的过程,根据射影几何中“点线结合的不变性”,具体通过射影前后任意两圆的公切线与圆的切点的唯一性,并且运用“标靶像坐标得切点切线算法”对所给像图片进行操作,求得切点的坐标,每对切点连线的交点即为圆心的像。
求得的结果如下表:点 A B C D E坐标(-194,-193,1577) (-97,-186,1577) (119,-169,1577) (67,113,1577) (-226,114,1577)(单位:像素)第二步,依靠成像过程光学中心—像点—物点三点共线的性质,用已知的像点坐标去标定对应的标靶圆心的坐标,再利用标靶上各点的几何关系,对待定系数进行求解,从而得到标靶圆心坐标;第三步,在已知标靶圆心在两个相机坐标系中的坐标的前提下,利用这些坐标求出坐标系变换矩阵。
再利用求出的变换矩阵求出一部相机在另一相机坐标系中的坐标,这样就可以求出两个相机的相对位置。
此外,根据投影过程中“共线不变性”和“交比不变性”对模型中的第一个步骤的结果进行评价,并对这两种方法的准确性和稳定性进行讨论,其中设计了恰当的算法对方法二进行了全面的评定,得出方法一具有局限性而方法二具有良好得准确性和稳定的结果。
在模型扩展中,我们建立了考虑畸变的非线性模型。
分析了理想像点坐标和实际有畸变的像点坐标之间的函数关系,从而提出了将非线性模型问题转换到线性模型下解决的方案。
关键词:照相机定位针孔模型射影变换交比坐标变换目录数码相机相对位置定位方法 (1)1.摘要 (1)2.问题重述 (3)3.问题分析 (3)4.模型假设 (3)5.符号说明 (4)6.模型建立与求解 (4)1)模型准备: (4)2)模型建立 (4)3)对问题一的解答: (6)a)问题分析: (6)b)算法:标靶像坐标的切线切点算法 (6)c)改进算法:基于罚函数思想的切点切线算法 (7)d)算法分析: (7)4)对问题二的回答: (7)5)求解标靶圆心在照相机坐标系下的坐标 (8)a)问题分析: (8)b)求解方法: (8)6)利用空间坐标变换法确定两部照相机的相对位置: (10)a)问题分析: (11)b)求解过程: (11)7.模型分析及检验 (12)1)对问题三的回答: (12)a)方法一:利用共线不变性对结果的检验 (12)b)方法二:基于射影变换交比不变性的检验方法 (13)2)模型分析 (16)8.模型拓展 (16)9.参考文献 (17)10.附录 (18)2.问题重述题目要求根据标靶的像和标靶进行对系统的标顶,最终找到两台照相机的相对位置。
数码相机定位方法探究曲建跃 吴修振 沈宁 指导教员:司守奎 孙玺菁(海军航空工程学院,烟台,264001)摘要:数码相机定位在交通监管等方面有广泛的应用,例如可以用数码相机摄制物体的相片确定物体表面某些特征点的位置。
双目定位是最常用的定位方法,即对物体上一个特征点,用两部固定于不同位置的相机摄得物体的像,分别获得该点在两部相机像平面上的坐标。
双目定位的关键是系统标定,即精确地确定两部相机的相对位置。
要确定两部相机的相对位置,首先应确定一个相机的像坐标系和靶标坐标系之间的转换关系,确定其内外部参数,即对一个相机进行标定。
在前三问中,本文从空间平面的几何关系入手,先对靶平面坐标进行旋转,平移和投影,然后借助于相机的小孔成像原理,得到了物与像的二维坐标关系模型,再通过抓取特征点对的坐标,用最小二乘法拟合,求得物与像二维坐标关系:⎥⎦⎤⎢⎣⎡−−+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−=⎥⎦⎤⎢⎣⎡7349.296064.5907971.00231.00907.07709.0i i i i Y X y x ,进而求得靶标上五个圆的圆心的像的物理坐标为)9751.495346.50(,−,)2821.494094.27(,−,)6651.475536.26(,,)0449.324853.17(−−,,)7349.296064.59(−−, ,其对应的像素坐标为)9724.3200944.195(,,)3925.4087137.197(,,)3726.6128259.203(,,)0880.5781279.505(,(此处采用矩阵坐标表示,原点选取图像左上角的顶点)。
然后通过具体点坐标对所建立的模型进行了检验,用模型求得的像坐标与实际像坐标的距离的均值作为精确度,其距离的均方差作为稳定性,得到模型的精确度为6659.1=∇,稳定性5804.0=P 。
第四问中,通过求得的相机的内外部参数,得到像坐标系与靶标坐标系之间的转换关系,然后通过求解方程组,得到两个相机坐标系间的坐标转换矩阵H ,从而完成了系统标定。
本文特色是使用的方法简单,快捷,可操作性强,并且具有很高的精度和稳定性。
关键字:双目相机标定,几何坐标变换,小孔成像,坐标抓捕,最小二乘拟合1 问题的提出现代生活越来越多地用到通过相机来确定某一物体的具体方位和位置,比如交通监管,道路交通事故现场的准确测量,以及机器人的目标定位等。
对物体上一个特征点,用两部固定于不同位置的相机摄得物体的像,分别获得该点在两部相机像平面上的坐标。
只要知道两部相机精确的相对位置,就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标,即确定了特征点的位置。
利用相机测量的精度取决与相机标定的精度,因此,建立一种理想的相机标定模型和方法显得尤为重要。
本题中即要求给出这样一个模型,并且利用给出的模型求出靶点在像平面内的点以及其精度。
2 问题的分析相机标定方法可分为三类:传统标定方法、主动视觉标定方法、相机自标定方法。
从问题给出的条件来看,比较适合用传统的标定方法。
为此,本文先通过深入分析相机的成像原理,建立了像坐标系和靶坐标系之间的转换模型,并通过最小二乘拟合的方法具体求得了转换关系,从而完成了对一个相机的标定,然后通过求解方程组得到两个相机之间的位置关系转换模型。
解题过程如图1:图13 模型的假设(1)相机中凸透镜的直径与物距相比可忽略不计,可用小孔成像原理近似代替;(2)相机中凸透镜的厚度忽略不计;(3)相机拍照时,忽略空气对光线的影响;(4)靶标在两个相机分别拍照时不发生移动;(5)拍照时,两个相机固定不动;4 符号说明M: 靶标平面wM: 像平面cl: 像距d: 物距;f : 凸透镜的焦距;y x −: 凸透镜光学中心处与主光轴垂直的平面;ω: 靶标平面与主光轴交点处且与主光轴垂直的面; ''y x −: 像平面上的坐标系; Y X −: 靶标面上的坐标系;y xˆˆ−: ω平面上的坐标系; v u −: 靶标面上原点位于靶标平面与主光轴交点处的辅助坐标系; v uˆˆ−: ω面上原点位于靶标平面与主光轴交点处的辅助坐标系; ),(00y x :()i i Y X ,坐标系的原点在v u −坐标系中的坐标;L : 靶标平面与的ω面的交线; s : 物的点到w M 面的距离;θ: 靶标平面与ω面的夹角;β: v uˆˆ−坐标系与v u −坐标系夹角; γ: Y X −坐标系与y xˆˆ−坐标系的夹角; []T R :相机的外部参数;H : 两个相机坐标系间的坐标转换矩阵;∇: 模型的精确度; P : 模型的稳定性;5 模型的建立与求解5.1 问题(1)的建立的求解对问题(1),本文通过对相机成像原理的分析建立了单个相机的标定模型,具体建模过程如下。
5.1.1本文建立的模型图为:图2γyˆ)vˆu)i 图35.1.2 对模型图的分析和求解过程求解过程中,本文从空间平面的几何关系入手,运用了四次点的平面坐标变换,一次平移,两次旋转,一次投影,在二维平面上建立起了靶标平面与像平面在空间上在的转换关系。
靶标平面与v u ˆˆ−坐标系的相互关系是多样性的,靶标平面与v u ˆˆ−坐标系呈θ角的同时,它们的交线跟^i x 轴往往是呈一定夹角,设其为β角,现将靶标平面上的()i i Y X ,坐标转化成v uˆˆ−坐标系上的()'',i i y x 坐标]1[,即得: ⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡00^^cos sin sin cos cos 001cos sin sin cos y x Y X y x i i i i γγγγθββββ 再利用凸透镜的小孔成像原理,近似得到点()i i Y X ,与其在像平面上所对应的点的坐标),(i y x i 的对应关系⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡00cos sin sin cos cos 001cos sin sin cos 00y x Y X s d l sd ly x i i i i γγγγθββββ 即⎥⎦⎤⎢⎣⎡+−−+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−+−−−−=⎥⎦⎤⎢⎣⎡θββθβββθγγβγθβγβγθββγβθγβγcos cos sin cos sin cos cos cos cos sin sin sin cos cos cos sin cos cos sin cos sin sin cos sin cos cos 0000y x y x s d l Y X s d l y x i i i i 由于θγβ,,和00y x ,以及d l ,都是固定值,又因为通常d 远大于l ,因而s 可近似看做与i X ,i Y 无关,因此可以用新的参数代替原来的参数,使问题进一步简化,分别用f e d c b a ,,,,,代替原来参数,把上式简化,得⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡f dY cX e bY aX f e Y X d c b a y x i i i i i i i i其中)sin cos sin cos (cos βθγβγ−−=s d la )cos cos sin cos sin (γθββγ−−−=s d l b)sin cos cos cos (sin γθβγβ+−=s d l c)cos cos cos sin sin (βθγγβ+−−=sd l d)(θββcos sin cos 00y x s d l e −−=)cos cos sin (00θββy x sd l f +−=令⎥⎦⎤⎢⎣⎡=d c b a R ,⎥⎦⎤⎢⎣⎡=f e t ,则可得相机的外部参数,即[]T R ,以及标定的像坐标系与靶标坐标系之间的转换关系,记为:T RM M w c +=其中c M 代表像坐标系,w M 代表靶坐标系。
把转换关系分解得fdY cX y e bY aX x i i i i i i ++=++=5.2 问题(2)的求解 5.2.1 像坐标求解过程通过Matlab与画图软件结合与能用,实现了对像坐标特征值点的直接抓捕,本文规定像素坐标的原点取在像平面左上角的顶点,经过处理,得到了靶坐标和像坐标的16 组数据,分别为表1),(i i Y X),(i i y x(-12.0000,100.0000) (-60.8466,51.3228) (-12.0000,0)(-70.3704,-32.2751) (12.0000,100.0000) (-39.1534,51.8519) (12.0000,0)(-50.0000,-30.4233) (30.0000,112.0000) (-23.0159,59.7884) (100.0000,112.0000) (34.6561,55.0265) (30.0000,88.0000) (-24.0741,38.8889) (100.0000,88.0000) (32.5397,35.4497) (88.0000,100.0000) (-12.9630,50.2646) (88.0000,0)(-50.0000,-30.4233) (112.0000,100.0000) (43.3862,46.2963) (112.0000,0) (27.7778,-30.1587) (0,12.0000)(-59.2593,-21.9577) (100.0000,12.0000) (20.1058,-23.0159) (0,-12.0000)(-60.8466,-40.4762) (100.0000,-12.0000)(17.1958,-39.9471)5.2.2 最小二乘法拟合参数[]e b a ,[]f d c本文用求得的前十二组数据进行最小二乘法拟合,后四组数据进行精度和稳定性分析。
通过Matlab编程,求得回归系数为[]e b a=[]]6064.590907.07709.0−,[]f d c =[]7349.297971.00231.0−−则⎥⎦⎤⎢⎣⎡−−+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−=⎥⎦⎤⎢⎣⎡7349.296064.5907971.00231.00907.07709.0i i i i Y X y x从靶图中读出五个圆心坐标为)1000(,,)10030(, ,)100100(, ,)0100(, ,)00(, ,代入上式可得五个圆心对应的像坐标为)9751.495346.50(,−,)2821.494094.27(,−,)6651.475536.26(,,)0449.324853.17(−−,,)7349.296064.59(−−, ,对应的像素坐标为)9724.3200944.195(,,)3925.4087137.197(,,)3726.6128259.203(,,)0880.5781279.505(,。