长沙理工大学概率论试题7

长沙理工大学数计学院概率论与数理统计 模拟试题一考试类别：闭 考试时量：120 分钟一．填空题(每空2分，共32分)：1．设7.0)(,4.0)(=⋃=B A P A P ,若B A ,互不相容,则=)(B P ; 若B A ,独立,则=)(B P .2．若)4,1(~N X ,则~21-=X Y .3．已知6.0)(,8.0)(=-=B A P A P ,则=⋃)(B A P ,=)|(A B P .4．从(0,1)中随机地取两个数b a ,,则b a -大于0的概率为 .5．若],2,0[~πU X 则12-=X Y 的概率密度函数为=)(y f . 6．随机变量),2(~2σN X ,若3.0)40(=<<X P ,则=<)0(X P . 7．设X 的分布列为5.0)1()1(===-=X P X P ,则X 的分布函数为=)(x F .8．设随机变量X 有分布函数⎪⎩⎪⎨⎧≥<≤<=2,120,sin 0,0)(ππx x x A x x F , 则=A ,=<)6|(|πX P .9．一颗均匀骰子被独立重复地掷出10次,若X 表示3点出现的次数,则X ~ . 10．设),(Y X 的联合分布列为则=a ,Y 的分布列为 ;若令2)2(-=X Z ,则Z 的分布列为 .11．若)9,2(~N X ,且)()(c X P c X P >=≤,则=c .二．选择题(每题3分，共12分)：1．设B A ,为两事件,且1)(0<<A P ,则下列命题中成立的是 ( )A. B A ,独立)|()|(A B P A B P =⇔B. B A ,独立⇔B A ,互不相容C. B A ,独立⇔Ω=⋃B AD. B A ,独立⇔0)(=AB P2．设⎪⎪⎩⎪⎪⎨⎧≥<≤<=1,110,20,0)(x x x x x F , 则 ( )A . )(x F 是一个连续型分布函数 B. )(x F 是一个离散型分布函数C. )(x F 不是一个分布函数D. 5.0)1(==X P3．设随机变量X 的概率密度函数为)(x f ,且)()(x f x f =-,)(x F 是X 的分布函数,则对任意实数a ,有 ( )A. ⎰-=-adxx f a F 0)(1)( B. ⎰-=-a dx x f a F 0)(21)(C. )()(a F a F =-D. 1)(2)(-=-a F a F4．设随机变量}5{},4{).5,(~),4,(~2122+≥=-≤=u Y P p u X P p u N Y u N X ,则 ( )A . 对任意实数21,p p u = B. 对任意实数21,p p u <C. 只对u 的个别值才有21p p =D. 对任意实数21,p p u >三．某工厂甲、乙、丙三车间生产同一种产品,产量分别占25%,35%,40%,废品率分别为5%,4%和2%.产品混在一起,求总的废品率及抽检到废品时,这只废品是由甲车间生产的概率. (9分)四．箱中装有5个黑球,3个白球,无放回地每次取一球,直至取到黑球为止.若X 表示取球次数,求X 的分布列,并求)31(≤<X P .( 9分) 五．设随机变量),(Y X 的联合概率密度函数为⎩⎨⎧<<<<=,010,10,),(2y x cxy y x f , 求: 1)常数c ; 2) )241,210(<<<<Y X P ;3)43(>X P ); 4))(Y X P >. (16分)六．在一盒子里有12张彩票,其中有2张可中奖.今不放回地从中抽取两次,每次取一张,令Y X ,分别表示第一、第二次取到的中奖彩票的张数,求),(Y X 的联合分布列. 七．设12,,,,n X X X ⋅⋅⋅是来自下列两参数指数分布的样本：()()1121211,120;,x e x x f x θθθθθθθ--≥≤⎧⎪=⎨⎪⎩其中()1,θ∈-∞+∞，()20,θ∈+∞，试求出1θ和2θ的最大似然估计. (16分)其它长沙理工大学数计学院概率论与数理统计 模拟试题一答案一．填空题1. 0.3 0.52. )1,0(N3. 0.8 0.254. 0.55. ⎩⎨⎧-≤≤-,011,1πy 6. 0.35 7. ⎪⎩⎪⎨⎧≥<≤--<1,111,5.01,0x x x 8. 1 0.5 9.)61,10(B10. 2/911. 2二．选择题 A C B A三．解: 设1A ={产品由甲厂生产}, 2A ={产品由乙厂生产},3A ={产品由丙厂生产},B ={产品是废品},由题意%40)(%,35)(%,25)(321===A P A P A P ；%5)|(1=A B P , %4)|(2=A B P , %2)|(3=A B P . 2分由全概率公式,∑==⨯+⨯+⨯==310345.002.040.004.035.005.025.0)|()()(i i i A B P A P B P ,6分从而由贝叶斯公式,36.00345.005.025.0)()|()()()()|(1111=⨯===B P A B P A P B P B A P B A P . 9分四． 解: 由题意知X 的可能取值为1,2,3,4,其分布列为,5615)2(,85)1(171518131815=⋅=====C C C C X P C C X P561)4(,565)3(1515383316152823=⋅===⋅==C C C C X P C C C C X P . 7分 )3()2())3()2(()31(=+===⋃==≤<∴X P X P X X P X P .1455655615=+=. 9分五．解: 1) 由⎰⎰+∞∞-+∞∞-=1),(dxdy y x f 有其它6|3122|21110310210210210102cy c dy y c dy x cy dxdy cxy =⋅==⋅==⎰⎰⎰⎰, 6=∴c ; 4分2)⎰⎰⎰⎰==<<<<21412141012026),()241,210(dydxxy dydx y x f Y X P=25663)411(2|31630130214121=-=⋅⎰⎰dx x dx y x ; 8分3)dxdy y x f Y X P X P ⎰⎰+∞+∞∞-=+∞<<∞->=>43),(),43()43(1672|3166111103102434343==⋅==⎰⎰⎰⎰dx x dy y x dydx xy ; 12分 4)⎰⎰⎰⎰⎰⋅===>>10031002|3166),()(dxy x dydx xy dxdy y x f Y X P xx yx52214==⎰dx x . 16分六．解: 每次只取一张彩票,要么取到中奖彩票,要么没取到中奖彩票,所以Y X ,的可能取值均为0或1,那么),(Y X 的联合分布列为,2215)0,0(11119112110=⋅===C C C C Y X P 335)1,0(11112112110=⋅===C C C C Y X P ,,335)0,1(11111011212=⋅===C C C C Y X P .661)1,1(1111111212=⋅===C C C C Y X P 6分七.解：似然函数()()1212121,,,;,;,nn i i L x x x f x θθθθ=⋅⋅⋅=∏()[)()12111,21min ni i x i neI x θθθθ=--+∞∑=(4分)要使()1212,,,;,n L x x x θθ⋅⋅⋅最大，必须min i x 1θ≥且()11ni i x θ=-∑应最小.故1θ的最大似然估计值为1θ=min i x . （8分）而2θ的最大似然估计值是使2121nL eλθθ-=取最大值的点. 此处()11ni i x λθ==-∑. （12分）故2θ=1n λ. 所以2θ的最大似然估计值为min i x x -最大似然估计量为1ˆθ=min i X，2ˆθ=min iX X -. （16分）长沙理工大学数计学院概率论与数理统计 模拟试题二卷 一.填空题(每空2分,共40分)1. 已知6.0)(,8.0)(=-=B A P A P ,则=⋃)(B A P , =)|(A B P.2. 从9,,2,1,0 这十个数字中任选三个不相同的数字,1A ={三个数字中不含0和5},2A ={三个数字中含有0和5},则=)(1A P ,=)(2A P .3. 设X ~)1(P ,Y ~)2(P ,且X 与Y 独立,则==+)2(Y X P .4. 若X ~)1,0(N ,Y ~)8,2(N ,X 与Y 独立,则32-+Y X ~ .5．设X 与Y 独立,2,1==DY DX ,则=-)32(Y X D .6．已知,4.0,36,25,===Y X DY DX ρ则=),(Y X Cov , =+)(Y X D.7. 设X 的分布函数=)(x F ⎪⎩⎪⎨⎧>≤<--≤1,111,5.01,0x x x ，则X 的分布列为 . 8. 随机变量),2(~2σN X ,若3.0)40(=<<X P ,则=<)0(X P . 9. 设),(Y X 的联合分布列为则=a ,Y 的分布列为 ;若令2)2(-=X Z ,则=EZ .10. 若)9,2(~N X ,且)()(c X P c X P >=≤,则=c . 11. 设随机变量X 的期望,1=EX 方差2=DX ,由车贝晓夫不等式知><-)3|1(|X P .12. 设Y X ,独立同分布,有共同的概率密度函数)(x f ,则=<)(Y X P .13. 设 ,,,1n X X 独立同分布,且11=EX ,则−→−∑=Pn i i X n 11 .14. 设74)0()0(,73)0,0(=≥=≥=≥≥Y P X P Y X P ,则=≥)0),(max(Y X P .15. 设 ,,,1n X X 独立同分布, ]2,0[~1U X ,则=≤∑=∞→)11(lim 1ni i n X n P .二. 单选题(在本题的每一小题的备选答案中,请把你认为正确答案的题号,填入题干的括号内,多选不给分.每题3分,共15分)1. 设随机变量X 的概率密度函数为)(x f ,且)()(x f x f =-,)(x F 是X 的分布函数,则对任意实数a ,有 ( )①. ⎰-=-adx x f a F 0)(1)( ②. ⎰-=-a dx x f a F 0)(21)(③. )()(a F a F =- ④. 1)(2)(-=-a F a F2. 设8.0)|(,7.0)(,8.0)(===B A P B P A P ,则 ( ) ①. A,B 互不相容 ②. A,B 相互独立 ③. B ⊂A ④. P(A-B)=0.13. 如果随机变量Y X ,满足)()(Y X D Y X D -=+,则必有 ( )①. X 与Y 独立 ②. X 与Y 不相关 ③. 0)(=Y D ④. 0)(=X D4. 4次独立重复实验中,事件A 至少出现一次的概率为80/81,则 ( ) ①.21 ②. 31 ③. 32 ④. 415. 设随机变量X 服从指数分布)3(E ,则=),(DX EX ( )①. (31,31) ②. )3,3( ③. )91,31( ④. )9,3(三. 计算题(共45分)1. 一仓库有10箱同种规格的产品,其中由甲,乙,丙三厂生产的分别为5箱,3箱,2箱,三厂产品的次品率依次为0.1,0.2,0.3,从这10箱产品中任取一箱,再从这箱中任取一件,求取得正品的概率?若确实取得正品,求正品由甲厂生产的概率.(8分)2. 设随机向量),(Y X 的联合密度函数为:⎩⎨⎧≤≤≤≤+=,020,10,),(2y x bxy x y x f求①常数b; ②)1(≥+Y X P ; ③)21|1(<>X Y P ; ④讨论Y X ,的独立性. (12分)3. 袋中有5个红球,3个白球,无放回地每次取一球,直到取出红球为止,以X 表示取球的次数,求①X 的分布列,②))31(≤<X P ,③EX . (9分) 其它4. 某教室有50个座位,某班有50位学生,学号分别为1到50.该班同学上课时随机地选择座位,X 表示该班同学中所选座位与其学号相同的数目,求X 的期望EX .(8分) ５．设12,,,n X X X 为总体X 的一个样本，X 的密度函数:(1),01()0,x x f x ββ⎧+<<=⎨⎩其他， 0β>, 求参数β的矩估计量和极大似然估计量。

长沙理工大学高等数学试题及答案一、单项选择题（本大题共5小题，每小题2分，共10分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设f(x)=lnx ，且函数ϕ(x)的反函数1ϕ-2(x+1)(x)=x-1，则[]ϕ=f (x)（ ） ....A B C D x-2x+22-x x+2 ln ln ln ln x+2x-2x+22-x2．()002lim 1cos tt x x e e dt x -→+-=-⎰（ ）A ．0B ．1C ．-1D ．∞ 3．设00()()y f x x f x ∆=+∆-且函数()f x 在0x x =处可导，则必有（ ）.lim 0.0.0.x A y B y C dy D y dy ∆→∆=∆==∆= 4．设函数,131,1x x x ⎧≤⎨->⎩22x f(x)=，则f(x)在点x=1处（ ）A.不连续B.连续但左、右导数不存在C.连续但不可导D. 可导5．设C +⎰2-x xf(x)dx=e ，则f(x)=（ ）2222-x -x -x -x A.xe B.-xe C.2e D.-2e二、填空题（本大题共10小题，每空3分，共30分）请在每小题的空格中填上正确答案。

错填、不填均无分。

6.设函数f(x)在区间[0，1]上有定义，则函数f(x+14)+f(x-14)的定义域是__________. 7．()()2lim 1_________n n a aq aq aq q →∞++++<=8．arctan lim _________x x x→∞= 9.已知某产品产量为g 时，总成本是2g C(g)=9+800，则生产100件产品时的边际成本100__g ==MC 10.函数3()2f x x x =+在区间[0，1]上满足拉格朗日中值定理的点ξ是_________.11.函数3229129y x x x =-+-的单调减少区间是___________.12.微分方程3'1xy y x -=+的通解是___________.13.设2ln 2,6a a π==⎰则___________.14.设2cos x z y =则dz= _______. 15.设{}2(,)01,01y D D x y x y xedxdy -=≤≤≤≤=⎰⎰，则_____________.三、计算题（一）（本大题共5小题，每小题5分，共25分）16.设1x y x ⎛⎫= ⎪⎝⎭，求dy. 17.求极限0ln cot lim ln x x x+→18.求不定积分.19.计算定积分I=0.⎰ 20.设方程2z x 2e 1y xz -+=确定隐函数z=z(x,y)，求','x y z z 。

长沙理工大学考试试卷……………………………………………………………………………………………………… 试卷编号 01 拟题教研室（或教师）签名 教研室主任签名 ……………………………………………………………………………………………………… 课程名称（含档次） 概率论与数理统计B 课程代号专 业 层次（本、专） 本科（城南） 考试方式（开、闭卷） 闭一、填空题(本大题总分10分，每小题2分)1 . 某射手向一目标连续射击两次，用i A 表示事件“第i 次射击命中目标”，1,2i =，则12(A A )(⋃)A A 21表示事件( 两次射击中仅一次命中目标 )2 . 设(X ，Y)服从区域}4y x y){(x,D 22≤+=上的均匀分布，则=>+)3Y P(X 22( 1/4 )3 . 若随机变量X 的数学期望为μ，方差为σσ(,2＞0)，则用切比雪夫不等式估计得{3}P X μσ-≥≤（ 1/9 ）4 . 设X 服从区间[0，2]上的均匀分布，Y=X 2，则cov(X,Y)=（ 2/3 ）5 . 评价参数的估计量优劣的标准有( 无偏性 )、有效性和一致性。

二、单项选择题(本大题总分20分，每小题5分)则2 0.5 ②0.3 ③0.09 ④0.212 . 设(X ，Y)的概率密度为⎩⎨⎧≤≤≤≤=其它01y 1,0x 01y)f(x,，则随机变量X 与Y（ ④ ）① 相关 ② 不相关③ 不相关但不独立 ④ 不相关且独立3 . 从0，1，…，9十个数字中随机地有放回地接连抽取四个数字，则“8”至少出现一次的概率为( ② )4 0.1 ② 0.3439 ③ 0.4 ④ 0.6561 4 . 设随机变量X 的密度函数p(x)满足：p(x)x)p(=-，F(x)是X 的分布函数，则对任意a >0,则a)X P(>=（ ① ）①F(a)]2[1- ②12F(a)- ③F(a)2- ④)2F(a 1-第 1 页（共 2 页）三、计算题(本大题总60分,每小题12分)1 . 三人独立地去破译一个密码,他们能译出的概率分别为413151、、,求(1)将此密码译出的概率, (2)恰好有一个人译出此密码的概率. 1. 1.解.：设{},1,2,3i A i ==第i 人能破译,则 (1) ()()3i 123123i=1423P(A )11()()10.6534P A A A P A P A P A =-=-=-⨯⨯=(6分) (2) ()()()123123123P A A A P A A A P A A A ++(8分)()()()123123123()()()()()()P A P A P A P A P A P A P A P A P A =++(10分)1234134211353453453430=⨯⨯+⨯⨯+⨯⨯=2 . 令cos πY =求：（1）Y 的分布律；（2）E （Y ）。

习题一1．设C B A ,,为随机试验的三个随机事件，试将下列事件用C B A ,,表示出来．（1）仅仅A 发生；（2）所有三个事件都发生；（3）A 与B 均发生，C 不发生；（4）至少有一个事件发生；（5）至少有两个事件发生；（6）恰有一个事件发生；（7）恰有两个事件发生；（8）没有一个事件发生；（9）不多于两个事件发生．解：（1）C B A ；（2）ABC ；（3）C AB ；(4)C B A ；(5)AC BC AB ；(6)C B A C B A C B A ；（7）C AB C B A BC A ；（8）C B A ；（9）ABC ．2．写出下列随机试验的样本空间（1）同时掷三颗骰子，记录三颗骰子的点数之和；（2）将一枚硬币抛三次，观察出现正反面的各种可能结果；（3）对一目标进行射击，且到击中5次为止，记录射击的次数；（4）将一单位长的线段分为三段，观察各段的长度；（5）从分别标有号码1，2， ，10的10个球中任意取两球，记录球的号码．解：（1）{3，4，5， ，18}；（2）{}TTT THT TTH THH HTT HTH HHT HHH ,,,,,,,;(3) {5,6,7, }；(4) }{1,0,0,0:),,(=++>>>z y x z y x z y x ;(5)}{n m n m n m ≠≤≤≤≤,101,101:),(．3．将12个球随机地放入20个盒子，试求每个盒子中的球不多于1个的概率．解：设)(A P 表式所求的概率，则：12122020!12.)(C A P =≈0.01473． 4．将10本书任意地放在书架上，其中有一套4卷成套的书，求下列事件的概率：（1）成套的书放在一起；（2）成套的书按卷次顺序排好放在一起．解： （1）设)(A P 表示所求的概率，则：)(A P =301!10!4!7=⋅． （2）设)(B P 表示所求的概率，则：)(B P =7201!10!7=． ５．一辆公共汽车出发前载有５名乘客，每一位乘客独立的在七个站中的任一个站离开，试求下列事件的概率：（1）第七站恰好有两位乘客离去；（2）没有两位及两位以上乘客在同一站离去． 解：5名乘客在七个站中的任意一个站离开的结果总数57=n ．（1）第七站恰好有两位乘客离去，其方法数3256⋅=C m ，故设)(A P 为所求概率，则：1285.076)(5325=⋅=C A P ． （2）设=B {没有两位及两位以上乘客在同一站离去}，则：1499.07!5)(557=⋅=C B P ． 6．有一个随机数发生器，每一次等可能的产生9,,2,1,0 十个数字，由这些数字随机编成的n 位数码（各数字允许重复），从全部n 位数码中任意选取一个，其最大数字不超过k （9≤k ）的概率．解：设)(A P 表式所求的概率，则由全部n 位数码的总数为n10，得：n nk A P 10)1()(+=． ７．一元件盒中有50个元件，期中25件一等品，15件二等品，10件次品，从中任取10件，求：（1）恰有两件一等品，两件二等品的概率；（2）恰有两件一等品的概率；（3）没有次品的概率．解：（1）设)(A P 为所求概率，则：41050610215225104397.6)(-⨯=⋅⋅=C C C C A P ． （2）设)(B P 为所求概率，则：03158.0)(1050825225=⋅=C C C B P ． （3）设)(C P 为所求概率，则：0825.0)(10501040==C C C P ． ８．有10个人分别佩戴者标号从1号到10号的纪念章，任意选出3人，记下其纪念章的号码，试求：（1）最小的号码为5的概率；（2）最大的号码为5的概率．解：从10人中任意选3人纪念章号码的总数为310C n =，（1）最小号码为5，则余下2个在6—10中选，即25C m =，设)(A P 为所求概率，则： 083.0)(31025==C C A P ． （2）同理设)(B P 为所求概率，则：05.0)(31024==C C A P ． 9．设事件B A ,及B A 的概率分别为q p ,和r ，试求：)(),(),(),(B A P B A P B A P AB P ． 解：r q p B A P B P A P AB P -+=-+=)()()()( ；p r A P A B P A B P B A P -=-=-=)()()()( （单调性）； q r B P B A P B A P B A P -=-=-=)()()()( （单调性）；r B A P B A P B A P -=-==1)(1)()( ．10．一批产品共100件，其中5件不合格．若抽检的5件产品中有产品不合格，则认为整批产品不合格，试问该批产品被拒绝接收的概率是多少？解：（法一）设i A ={抽检的5件产品中第i 件不合格}，i =1,2,3,4,5则所求概率为：∑===5151)()(i i i i A P A P )()()()()(54321A P A P A P A P A P ++++= 2304.0510055510019545510029535510039525510049515≈++++=C C C C C C C C C C C C C C ． （法二） 2304.01)(1)(5100595051≈-=-==C C A P A P i i ． 11．设A 和B 是试验E 的两个事件，且21)(,31)(==B P A P ，在下述各种情况下计算概率)(A B P ：（1）B A ⊂；（2）A 和B 互不相容；（3）81)(=AB P ． 解：（1）613121)()()()(=-=-=-=A P B P A B P A B P ．（2）21)()(==B P A B P ． （3）838121)()()()(=-=-=-=AB P B P A B P A B P ． 12．现有两种报警系统A 与B ，每种系统单独使用时，系统A 有效的概率为0.92，系统有效的概率为0.93 ．装置在一起后，至少有一个系统有效的概率则为0.988，试求装置后：（1）两个系统均有效的概率；（2）两个系统中仅有一个有效的概率．解：（1）所求概率为)(AB P ，得：)()()()(B A P B P A P AB P -+=862.0988.093.092.0=-+=；（2）所求概率为)(B A B A P ，得：)(B A B A P )()(B A P B A P +=)()()()(AB P B P AB P A P -+-=126.0862.0293.092.0=⨯-+=．13．10把钥匙上有3把能打开门，今任取2把，求能打开门的概率．解：（法一）从10把钥匙中任取2把的试验结果总数45210==C n ，能打开门意味着取到的二两把钥匙至少有一把能打开门，其取法数24171323=+=C C C m ，故设)(A P 为所求概率，则：158)(210231713=+=C C C C A P ．（法二）记A 为“能打开门”，则=A “两把钥匙皆开不了门”，于是158452111)(1)(21027=-=-=-=C C A P A P ． 14．一个盒子中有24个灯泡，其中有4个次品，若甲从盒中随机取走10个，乙取走余下的14个，求4个次品灯泡被一人全部取走的概率．解：设=A {次品灯泡全部被甲取走}，=B {次品灯泡全部被乙取走}，则B A ,互不相容，所求概率为：)()()(B P A P B A P += 1140.0424414424410=+=C C C C ． 15．设将5个球随意地放入3个盒子中，求每个盒子内至少有一个球的概率．解：5个球随意地放入3个盒子中事件总数53=n ，3个盒子中一个或两个盒子中有球数为332533153p C p C m ++=，设所求概率为)(A P ，则：8150331)(533253315=++-=p C p C A P ． 16．已知1A 和2A 同时发生，则A 必发生，证明：1)()()(21-+≥A P A P A P ． 证明：由已知，A A A ⊂21，再由单调性，)()(21A P A A P ≤，则)()()()()(212121A A P A P A P A A P A P -+=≥,1)(021≤≤A A P ．1)()()()()()()(21212121-+≥-+=≥∴A P A P A A P A P A P A A P A P ．17．掷一枚均匀硬币直到出现三次正面才停止，问正好在第六次停止的情况下，第五次也是正面的概率是多少？解：设=A {第五次出现正面}，=B {第六次停止}，则：52)21()21()()()|(256146===C C B P AB P B A P ． 18．证明：0)()|(>>A P B A P ，则)()|(B P A B P >． 证明：)()|()()()()|(B P B A P AB P A P AB P A B P =>=，即证． 19．设事件B A ,互不相容，且0)(>B P ，试证：)(1)()|(B P A P B A P -=． 证明：)(1)()()()|(B P A P B P B A P B A P -=互不相容． 20．将两颗均匀骰子同时掷一次，已知两个骰子的点数之和是奇数，求两个骰子的点数之和小于8的概率．解：此事件的样本空间由36个样本点组成，设=A {两个骰子的点数之和小于8}，=B {两个骰子的点数之和是奇数}，则3618)(=B P ，3612)(=AB P ，于是： 322131)()()|(===B P AB P B A P ． 21．设10件产品中有4件是次品，从中任取两件，试求在所取得的产品中发现有一件是次品后，另一件也是次品的概率．解：设=A {所取得两件中至少有一件是次品}，=B {所取得两件产品都是次品}，B AB A B =∴⊂, ．而321)(1)(21026=-=-=C C A P A P ，152)(21024==C C B P ，所求概率为：5132152)()()()()|(====A P B P A P AB P A B P ． 22． 10件产品有6件是正品，4件次品，对它们逐一进行检查，问下列事件的概率是多少？（1）最先两次抽到的都是正品；（2）第一、三次抽到正品，第二、四次抽到次品；（3）在第五次检查时发现最后一个次品．解：设i A ={第i 次抽到的是正品}，i =1,2,3,4,5,6．则 (1)3195106)|()()(12121=⋅=⋅=A A P A P A A P ; (2) )(4321A A A A P )|()|()|()(3214213121A A A A P A A A P A A P A P =141738594106=⋅⋅⋅=； (3) 设=B {第五次检查时发现最后一个次品}，则2104)(151********=*=C C C C C B P ． 23．某人忘记电话号码的最后一个数字，他仅记得最末一位数字是偶数．现在他试着拨最后一个号码，求他拨号不超过三次而接通电话的概率．解：设=A {接通电话}，=i B {拨号i 次}，i =1，2，3．i B 构成样本空间的一个划分，由全概率公式：)|()()|()()|()()(332211B A P B P B A P B P B A P B P A P ++=532110321522121=⨯+⨯+⨯=． 24．某型号的显像管主要由三个厂家供货，甲、乙、丙三个厂家的产品分别占总产品和的25%、50%、25%，甲、乙、丙三个厂的产品在规定时间内能正常工作的概率分别是0.1、0.2、0.4，求一个随机选取的显像管能在规定时间内正常工作的概率．解：设A ={能在规定时间内正常工作}，i B ={选取第i 个厂家的产品}，i =1，2，3．则由全概率公式：)|()()|()()|()()(332211B A P B P B A P B P B A P B P A P ++=225.04.025.02.05.01.025.0=⨯+⨯+⨯=．25．两批同类产品各自有12件和10件，在每一批产品中有一件次品，无意中将第一批的一件产品混入第二批，现从第二批中取出一件，求第二批中取出次品的概率．解：设=B {第二批中取出次品}，=A {第一批的次品混入第二批}，A A ,构成样本空间的一个有限划分，由全概率公式：0985.01111211112121)|()()|()()(=⨯+⨯=+=A B P A P A B P A P B P ． 26．在一个盒子中装有15个乒乓球，其中有9个新球，在第一次比赛时任意取出三个球，比赛后仍放回原盒中，第二次比赛时，同样任意的取出三个球，求第二次取出三个新球的概率．解：设B={第二次取出3个新球}．可以看出，直接确定B 的概率)(B P 是困难的，原因是，第一次比赛之后，12个乒乓球中的新、旧球的分布情况不清楚，而一旦新旧球的分布情况明确了，那么相应的概率也容易求得．为此，设i A ={第一次取到的3个球中有i 个新球}， i =0，1，2，3．容易判断3210,,,A A A A 构成一个划分．由于3,2,1,0,)(315369==-i C C C A P i i i ，又3,2,1,0,)|(31539==-i C C A B P i i ． 由全概率公式，得：)|()()(30i i i A B P A P B P ∑==∑=--=3023*******)(i i i i C C C C 0893.02070251680756075601680≈+++=． 27．仓库中存有从甲厂购进的产品30箱，从乙厂购进的同类产品25箱，甲厂的每箱装12个，废品率为0.04，乙厂的每箱装10个，废品率0.05，求：(1)任取一箱，从此箱中任取一个为废品的概率；(2)将所有产品开箱后混放，任取一个为废品的概率．解：(1)设=B {取出的是废品}，=A {从甲厂取出}，A A ,构成一个划分，则)|()()|()()(A B P A P A B P A P B P +=0441.005.010251230102504.0102512301230=⨯⨯+⨯⨯+⨯⨯+⨯⨯=(2) 0441.010********.0102504.01230=⨯+⨯⨯⨯+⨯⨯ 28．已知一批产品中96%是合格品，用某种检验方法辨认出合格品为合格品的概率是0.98，而误认废品是合格品的概率是0.05，求检查合格的一件产品确系合格的概率．解： 设A ={检查合格产品}，B ={确系合格}．由已知，05.0)|(,98.0)|(,96.0)(===B A P B A P B P ， 由贝叶斯公式：)()|()()|(A P B A P B P A B P =)|()()|()()|()(B A P B P B A P B P B A P B P += 9979.005.004.098.096.098.096.0≈⨯+⨯⨯=． 29．已知5%的男人和0.25%的女人是色盲者，现随机挑选一人，此人恰为色盲者，问此人 是男人的概率为多少（假设男人女人各占总人数的一半）．解：设=A {色盲者}，=B {男人}， B B ,构成样本空间的一个划分，且05.0)|(=B A P ， 0025.0)|(=B A P ，由贝叶斯公式：)()|()()|(A P B A P B P A B P = )|()()|()()|()(B A P B P B A P B P B A P B P +=9524.00025.02105.02105.021=⨯+⨯⨯=． 30．设某种病菌在人口中的带菌率为0.03，由于检验手段不完善，带菌者呈阳性反应的概 率为0.99，而不带菌者呈阳性反应的概率为0.05，若某人检查结果是呈阳性反应，他是带菌者的概率是多少？解：设=A {结果呈阳性}，=B {是带菌者}，则B B ,构成样本空间的一个划分，且 99.0)|(=B A P ，05.0)|(=B A P ，由贝叶斯公式：)()|()()|(A P B A P B P A B P =)|()()|()()|()(B A P B P B A P B P B A P B P += 3798.005.097.099.003.099.003.0=⨯+⨯⨯=． 31．证明：如果)|()|(B A P B A P =，则事件A 和B 相互独立． 证明：由已知和条件概率公式，有)()()()(B P B A P B P AB P =，即)()()()(AB P B P B A P B P =， 即)())(1()()(AB P B P AB A P B P -=-，又A AB ⊂，上式得：)()](1[)]()()[(AB P B P AB P A P B P -=-，有)()()(B P A P AB P =，即A 和B 相互独立．32．设一个n 位二进制数是由n 各“0”或“1”数字组成，每一位出现错误数字的概率是p ，各位数字出现错误与否是独立的，问组成一个不正确的这类二进制数的概率是多少？ 解：每一位出现正确数字的概率是p -1，由已知，各位数字出现正确与否也是独立的，于是所求概率nP A P )1(1)(--=．33.设事件C B A ,,相互独立，且21)(,31)(,41)(===C P B P A P ，试求： （1）三个事件都不发生的概率；（2）三个事件中至少有一个事件发生的概率；（3）三个事件中恰有一个事件发生的概率；（4）至多有两个事件发生的概率.解：（1）41)211)(311)(411()()()()(=---==C P B P A P C B A P ； （2）43411)(1)(=-=-=C B A P C B A P ； （3）)(C B A C B A C B A P )()()(C B A P C B A P C B A P ++=2411213243213143213241=⋅⋅+⋅⋅+⋅⋅=； （4）)()()(1)(1C P B P A P ABC P -=-24232131411=⋅⋅-=． 34．甲袋中有3只白球，7只红球，15只黑球；乙袋中有10只白球，6只红球，9只黑球．从两袋中各取一球，试求两球颜色相同的概率．解：设C B A ,,表示两球同为白色、红色和黑色，C B A ,,互不相容，则所求概率为：)()()()(C P B P A P C B A P ++= 3312.025925152562572510253=⨯+⨯+⨯=． 35．两部机床独立的工作，每部机床不需要工人照管的概率分别为0.9和0.85，试求：(1)两部均不需照管的概率； (2)恰有一部需要照管的概率；(3)两部同时需要照管的概率．解：设=A {甲机床不需要工人照管}，=B {乙机床不需要工人照管}，则9.0)(=A P ，85.0)(=B P ，(1)765.085.09.0)()()(=⨯==B P A P AB P (2))()()()()()()(B P A P B P A P B A P B A P B A B A P +=+=22.085.01.015.09.0=⨯+⨯= (3) 015.015.01.0)()()(=⨯==B P A P B A P ．36．求下列系统（图1.6）能正常工作的概率，其框图的字母代表组件，字母相同，下标不同的均为同一类组件，知识装配在不同的位置，A 类组件正常工作的概率为a γ，B 类组件正常工作的概率为b γ，C 类为c γ．解：(1)所求概率为)]()()()[()()()]([BC P C P B P A P C B P A P C B A P -+==c b a c a b a γγγγγγγ-+=．(2)所求概率为)()()()()(5421635241635241A A A A P A A P A A P A A P A A A A A A P -++= )()()(65432165326431A A A A A A P A A A A P A A A A P +--，又654321,,,,,A A A A A A 相互独立，则)33(33)(422642635241a a a a a a A A A A A A P γγγγγγ+-=+-= ．(3)所求概率为 )()()()]())([(22112211n n n n B A P B A P B A P B A B A B A P =)]()()([)]()()()][()()([22221111n n n n B A P B P A P B A P B P A P B A P B P A P -+-+-+= n b a b a )(γγγγ-+=．习题二1、一批晶体管中有9个合格品和3个不合格品，从中任取一个安装在电子设备上，如果取出不合格品不再放回，求在取得合格品以前已取出的不合格品数的概率．解：设在取得合格品以前已取出的不合格品数为随机变量X ，则X 的所有可能取值为：0，1，2，3。

第一章 概率论的基本概念 练习1.1 样本空间、随机事件一、写出以下随机试验的样本空间：1.从两名男乒乓球选手B A ,和三名女乒乓球选手,,C D E 中选拔一对选手参加男女混合双打，观察选择结果。

2.10件产品中有4件次品，其余全是正品，从这10件产品中连续抽取产品，每次一件，直到抽到次品为止，记录抽出的正品件数。

二、有三位学生参加高考，以i A 表示第i 人考取（1,2,3i =）.试用i A 表示以下事实： 1.至少有一个考取；2.至多64738291有两人考取；3.恰好有两人落榜。

三、投掷一枚硬币5次，问下列事件A 的逆事件A 是怎样的事件？1. A 表示至少出现3次正面；2. A 表示至多出现3次正面；3. A 表示至少出现3次反面。

四、袋中有十个球，分别编有1至10共十个号码，从其中任取一个球，设事件A 表示“取得的球的号码是偶数”， 事件B 表示“取得的球的号码是奇数”， 事件C 表示“取得的球的号码小于5”，则,,,,,C A C AC A C A B AB ⋃-⋃分别表示什么事件？五、在某系的学生中任选一名学生，令事件A 表示“被选出者是男生”；事件B 表示“被选出者是三年级学生”；事件C 表示“被选出者是运动员”。

（1）说出事件C AB 的含义；（2）什么时候有恒等式C C B A = ; (3) 什么时候有关系式B C ⊆正确; （4）什么时候有等式B A =成立。

练习1.2 概率、古典概型一、填空1.已知事件A ，B 的概率()0.7,()0.6P A P B ==,积事件AB 的概率()0.4P AB =,则()P A B ⋃= , ()P A B -= , ()P A B ⋃= , ()P A B ⋃= ,()P AB = , ()P A AB ⋃= .2. 设B A ,为两个事件，7.0)(=B P ,()0.3P AB =,则=+)(B A P .3. 设B A ,为两个任意不相容事件，,则=-)(B A P .4. 设B A ,为两个事件，5.0)(=A P ,=-)(B A P 0.2，则=)(AB P . 5. 已知,41)()()(===C P B P A P =)(AB P 0，61)()(==BC P AC P ，则C B A ,,全不发生的概率为 .二、设B A ,是两事件，且()0.6P A =，()0.7P B =,求(1) 在什么条件下，()P AB 取到最大值？ (2) 在什么条件下，()P AB 取到最小值？ 三、一批产品20件，其中3件次品，任取10件，求(1) 其中恰有一件次品的概率；(2) 至少有一件次品的概率。

科目代码：F1003 科目名称：概率论与数理统计
一、考试要求
主要考察考生是否掌握了概率论与数理统计的基本概念、基本理论和基本方法，包括概率、随机变量、统计量、抽样分布等基本概念，数字特征的计算，概率论基本公式、极限定理、点估计和区间估计的应用，以及是否具备运用基本理论和基本方法，分析解决实际概率问题和参数估计的能力。

二、考试内容
1、概率论基本公式的应用与计算；
2、随机变量的分布：分布函数、分布列、概率密度函数以及联合分布、边缘分布、条件分布；
3、随机变量的期望、方差、协方差、相关系数、特征函数的计算；
4、大数定理和中心极限定理的应用；
5、常用统计量和抽样分布；
6、矩估计法、极大似然法的应用、点估计量的性质和正态总体参数的区间估计。

三、题型
试卷满分为150分，其中：填空选择题占30%，计算分析题占70%。

四、参考教材
1.《概率论与数理统计》, 邓集贤，杨维权，司徒荣，邓永录著, 高等教育出版社，2009，第四版.
2．《概率论与数理统计》．梁小林、谢永钦主编．复旦大学出版社，2015，第二版.。

2020年大学必修课概率论与数理统计必考题及答案（完整版）一、单选题1、设X ～(1,)p β 12,,,,,n X X X ⋅⋅⋅是来自X 的样本，那么下列选项中不正确的是 (A)当n 充分大时，近似有X ～(1),p p N p n -⎛⎫⎪⎝⎭(B){}(1),k kn k n P X k C p p -==-0,1,2,,k n =⋅⋅⋅ (C ）{}(1),k k n k n kP X C p p n-==-0,1,2,,k n =⋅⋅⋅ (D ）{}(1),1k kn k i nP X k C p p i n -==-≤≤ 【答案】B2、设总体X 服从正态分布()212,,,,,n N X X X μσ是来自X 的样本，则2σ的最大似然估计为（A ）()211n i i X X n =-∑ （B ）()2111n i i X X n =--∑ （C ）211n i i X n =∑ （D ）2X 【答案】A3、1621,,,X X X 是来自总体），10(N ~X 的一部分样本，设：216292821X X Y X X Z ++=++= ，则YZ~（ ） )(A )1,0(N )(B )16(t )(C )16(2χ )(D )8,8(F【答案】D4、在假设检验问题中，犯第一类错误的概率α的意义是（ ） (A)在H 0不成立的条件下，经检验H 0被拒绝的概率 (B)在H 0不成立的条件下，经检验H 0被接受的概率 (C)在H 00成立的条件下，经检验H 0被拒绝的概率 (D)在H 0成立的条件下，经检验H 0被接受的概率 【答案】C5、在单因子方差分析中，设因子A 有r 个水平，每个水平测得一个容量为的样本，则下列说法正确的是___ __(A)方差分析的目的是检验方差是否相等 (B)方差分析中的假设检验是双边检验im(C)方差分析中包含了随机误差外,还包含效应间的差异(D)方差分析中包含了随机误差外,还包含效应间的差异【答案】D6、设X 的密度函数为)(x f ，分布函数为)(x F ，且)()(x f x f -=。

长沙理工大学数计学院概率论与数理统计 模拟试题一考试类别：闭 考试时量：120 分钟一．填空题(每空2分，共32分)：1．设7.0)(,4.0)(=⋃=B A P A P ,若B A ,互不相容,则=)(B P 0.3 ; 若B A ,独立,则=)(B P 0.5 .2．若)4,1(~N X ,则~21-=X Y )1,0(N .3．已知6.0)(,8.0)(=-=B A P A P ,则=⋃)(B A P 0.8 ,=)|(A B P 0.25 . 4．从(0,1)中随机地取两个数b a ,,则b a -大于0的概率为 0.5 .5．若],2,0[~πU X 则12-=X Y 的概率密度函数为=)(y f . 6．随机变量),2(~2σN X ,若3.0)40(=<<X P ,则=<)0(X P . 7．设X 的分布列为5.0)1()1(===-=X P X P ,则X 的分布函数为=)(x F .8．设随机变量X 有分布函数⎪⎩⎪⎨⎧≥<≤<=2,120,s i n 0,0)(ππx x x A x x F , 则=A ,=<)6|(|πX P .9．一颗均匀骰子被独立重复地掷出10次,若X 表示3点出现的次数,则X ~ . 10．设),(Y X 的联合分布列为则=a ,Y 的分布列为 ;若令2)2(-=X Z ,则Z 的分布列为 .11．若)9,2(~N X ,且)()(c X P c X P >=≤,则=c .二．选择题(每题3分，共12分)：1．设B A ,为两事件,且1)(0<<A P ,则下列命题中成立的是 ( )A. B A ,独立)|()|(A B P A B P =⇔B. B A ,独立⇔B A ,互不相容C. B A ,独立⇔Ω=⋃B AD. B A ,独立⇔0)(=AB P2．设⎪⎪⎩⎪⎪⎨⎧≥<≤<=1,110,20,0)(x x x x x F , 则 ( )A . )(x F 是一个连续型分布函数 B. )(x F 是一个离散型分布函数C. )(x F 不是一个分布函数D. 5.0)1(==X P3．设随机变量X 的概率密度函数为)(x f ,且)()(x f x f =-,)(x F 是X 的分布函数,则对任意实数a ,有 ( ) A.⎰-=-adxx f a F 0)(1)( B.⎰-=-adx x f a F 0)(21)(C. )()(a F a F =-D. 1)(2)(-=-a F a F4．设随机变量}5{},4{).5,(~),4,(~2122+≥=-≤=u Y P p u X P p u N Y u N X ,则 ( )A . 对任意实数21,p p u = B. 对任意实数21,p p u < C. 只对u 的个别值才有21p p = D. 对任意实数21,p p u >三．某工厂甲、乙、丙三车间生产同一种产品,产量分别占25%,35%,40%,废品率分别为5%,4%和2%.产品混在一起,求总的废品率及抽检到废品时,这只废品是由甲车间生产的概率. (9分)四．箱中装有5个黑球,3个白球,无放回地每次取一球,直至取到黑球为止.若X 表示取球次数,求X 的分布列,并求)31(≤<X P .( 9分) 五．设随机变量),(Y X 的联合概率密度函数为⎩⎨⎧<<<<=,010,10,),(2y x cxy y x f , 求: 1)常数c ; 2) )241,210(<<<<Y X P ;3)43(>X P ); 4))(Y X P >. (16分)六．在一盒子里有12张彩票,其中有2张可中奖.今不放回地从中抽取两次,每次取一张,令Y X ,分别表示第一、第二次取到的中奖彩票的张数,求),(Y X 的联合分布列.其它七．设12,,,,n X X X ⋅⋅⋅是来自下列两参数指数分布的样本：()()1121211,120;,x e x x f x θθθθθθθ--≥≤⎧⎪=⎨⎪⎩其中()1,θ∈-∞+∞，()20,θ∈+∞，试求出1θ和2θ的最大似然估计. (16分)长沙理工大学数计学院概率论与数理统计 模拟试题二考试类别:闭卷 考试时量:120分钟 试卷类型: A 卷一.填空题(每空2分,共40分) 1.已知6.0)(,8.0)(=-=B A P A P ,则=⋃)(B A P , =)|(A B P.2. 从9,,2,1,0 这十个数字中任选三个不相同的数字,1A ={三个数字中不含0和5},2A ={三个数字中含有0和5},则=)(1A P ,=)(2A P .3. 设X ~)1(P ,Y ~)2(P ,且X 与Y 独立,则==+)2(Y X P .4. 若X ~)1,0(N ,Y ~)8,2(N ,X 与Y 独立,则32-+Y X ~ .5．设X 与Y 独立,2,1==DY DX ,则=-)32(Y X D .6．已知,4.0,36,25,===Y X DY DX ρ则=),(Y X Cov , =+)(Y X D.7. 设X 的分布函数=)(x F ⎪⎩⎪⎨⎧>≤<--≤1,111,5.01,0x x x ，则X 的分布列为 .8. 随机变量),2(~2σN X ,若3.0)40(=<<X P ,则=<)0(X P . 9. 设),(Y X 的联合分布列为则=a ,Y 的分布列为 ;若令2)2(-=X Z ,则=EZ .10. 若)9,2(~N X ,且)()(c X P c X P >=≤,则=c . 11. 设随机变量X 的期望,1=EX 方差2=DX ,由车贝晓夫不等式知><-)3|1(|X P .12. 设Y X ,独立同分布,有共同的概率密度函数)(x f ,则=<)(Y X P.13. 设 ,,,1n X X 独立同分布,且11=EX ,则−→−∑=Pn i i X n 11 .14. 设74)0()0(,73)0,0(=≥=≥=≥≥Y P X P Y X P ,则=≥)0),(max(Y X P.15. 设 ,,,1n X X 独立同分布, ]2,0[~1U X ,则=≤∑=∞→)11(lim 1ni i n X n P .二. 单选题(在本题的每一小题的备选答案中,请把你认为正确答案的题号,填入题干的括号内,多选不给分.每题3分,共15分) 1. 设随机变量X 的概率密度函数为)(x f ,且)()(x f x f =-,)(x F 是X 的分布函数,则对任意实数a ,有( )①. ⎰-=-adxx f a F 0)(1)( ②. ⎰-=-adx x f a F 0)(21)(③. )()(a F a F =- ④. 1)(2)(-=-a F a F2. 设8.0)|(,7.0)(,8.0)(===B A P B P A P ,则 ( )①. A,B 互不相容 ②. A,B 相互独立 ③. B ⊂A ④. P(A-B)=0.13. 如果随机变量Y X ,满足)()(Y X D Y X D -=+,则必有 ( ) ①. X 与Y 独立 ②. X 与Y 不相关 ③. 0)(=Y D ④. 0)(=X D4. 4次独立重复实验中,事件A 至少出现一次的概率为80/81,则 ( ) ①. 21②. 31 ③. 32 ④. 415. 设随机变量X 服从指数分布)3(E ,则=),(DX EX ( )①. (31,31) ②. )3,3( ③. )91,31( ④. )9,3(三. 计算题(共45分)1. 一仓库有10箱同种规格的产品,其中由甲,乙,丙三厂生产的分别为5箱,3箱,2箱,三厂产品的次品率依次为0.1,0.2,0.3,从这10箱产品中任取一箱,再从这箱中任取一件,求取得正品的概率?若确实取得正品,求正品由甲厂生产的概率.(8分)2. 设随机向量),(Y X 的联合密度函数为:⎩⎨⎧≤≤≤≤+=,020,10,),(2y x bxy x y x f求①常数b; ②)1(≥+Y X P ; ③)21|1(<>X Y P ; ④讨论Y X ,的独立性. (12分)3. 袋中有5个红球,3个白球,无放回地每次取一球,直到取出红球为止,以X 表示取球的次数,求①X 的分布列,②))31(≤<X P ,③EX . (9分)4. 某教室有50个座位,某班有50位学生,学号分别为1到50.该班同学上课时随机地选择座位,X 表示该班同学中所选座位与其学号相同的数目,求X 的期望EX .(8分)５．设12,,,n X X X 为总体X 的一个样本，X 的密度函数:(1),01()0,x x f x ββ⎧+<<=⎨⎩其他， 0β>, 求参数β的矩估计量和极大似然估计量。

长沙理工大学考试试卷……………………………………………………………………………………………………… 试卷编号 07 拟题教研室（或教师）签名 教研室主任签名……………………………………………………………………………………………………… 课程名称（含档次） 概率论与数理统计B 课程代号专 业 层次（本、专） 本科（城南） 考试方式（开、闭卷） 闭一、填空题(本题总分10分,每小题2分)1 . 连续抛掷三次硬币，用i A 表示事件“第i 次抛掷的结果是正面向,1,2,3i =.则321A A A ⋃⋃表示事件( ).2 . 设随机变量X 的密度函数f(x)=⎩⎨⎧∈其他,0],0[,sin πx x A ，则常数A =（ ）. 3 . 设(X ，Y)在区域}x y 2,0x 0y){(x,D ≤≤≤≤=上服从均匀分布，则=>)1P (Y ( ).4 . 设随机变量列X 1,X 2,…,X n ,…独立同分布,它们的期望为μ,方差为σ2,Z n =∑=n 1i i Xn 1,则对任意正数ε,有∞→n lim P{|Z n -μ|≥ε}=（ ）. 5 . 设随机变量X ，Y 都服从区间[0，1]上的均匀分布，则E （X+Y ）=（ ）.二、单项选择题(本题总分20分,每小题5分)1 . 如果两个随机变量X 与Y 满足Y),D(X Y)D(X -=+则X 与Y 必（ ）. ① 相关 ② 不相关 ③ 不相关但不独立 ④ 不相关且独立2 . 从0，1，…，9十个数字中随机地有放回地接连抽取四个数字，则“8”至少出现一次的概率为( ).① 0.1 ② 0.3439 ③ 0.4 ④ 0.65613 . 若连续型随机变量X 的密度函数p(x)=⎩⎨⎧∈其它,0cos I x x ,则区间I 可以是（ ）.①［0，2π］ ②［0，π］ ③［0，23π］ ④［－2π，2π］ 4 . 设随机变量X 与Y 相互独立，且X ～),(2σμN ，Y ～),(2σμN ，则X ＋Y 的分布是（ ）.第 1 页（共 2 页）① ),(2σμN ② )2,(2σμN ③ ),2(2σμN ④ )2,2(2σμN .三、计算题(本题总分60分,每小题12分)1 . 某大学的全体男生中，有60%的人爱好踢足球，50%的人爱好打篮球，30%的人两项运动都爱好，求该校全体男生中：(1) 踢足球或打篮球至少爱好一项运动的概率有多大？(2) 不爱好踢足球，也不爱好打篮球的概率有多大？2 . 对一台仪器进行重复测试，直到发生故障为止，假定测试是独立进行的，每次测试发生故障的概率均为0.1，X 表示测试次数.求：（1）X 的分布列； （2）E （X ）.3 . 设二维随机变量()Y X ,的概率密度为22,1(,)0,Cx y x y f x y ⎧≤≤=⎨⎩其它. (1).试确定常数C ；(2).求边缘概率密度;（3）P （X+Y>1）.4. 设某公司有100件产品进行拍卖，每件产品的成交价为服从正态分布N(1000,100²)的随机变量，求这100件产品的总成交价不低于9.9万元的概率。

长沙理⼯⼤学概率论与数理统计下册考试参考题长沙理⼯⼤学模拟试卷第⼋套概率论与数理统计试卷⼀、填空题（每⼩题2分，共2×10＝20分）.1、假设1x，2x，…，n x是样本1ξ，2ξ，…，nξ的⼀个样本值或观测值，则样本均值x表⽰样本值的集中位置或平均⽔平，样本⽅差S2和样本修正⽅差S*2表⽰样本值对于均值x的_________________.2、样本⽅差S2和样本修正⽅差S*2之间的关系为_________________.3、矩估计法由英国统计学家⽪尔逊（Pearson）于1894年提出，它简便易⾏，性质良好，⼀直沿⽤⾄今. 其基本思想是：以样本平均值（⼀阶原点矩）ξ作为相应总体ξ的____________________；以样本⽅差（⼆阶中⼼矩）2S或者以样本修正⽅差2*S作为相应总体ξ的___________________________.4、总体未知参数θ的最⼤似然估计θ?就是___________________函数的极⼤值点.5、我们在估计某阶层⼈的⽉收⼊时可以说：“⽉收⼊1000元左右”，也可以说：“⽉收⼊在800元⾄1200元间”. 前者⽤的是___________，后者就是_________________.6、在确定的样本点上，置信区间的长度与事先给定的信度α直接有关. ⼀般来讲，信度α较⼤，其置信度（1－α）较⼩，对应置信区间长度也较短，此时这⼀估计的精确度升⾼⽽可信度降低；相反地，信度α较⼩，其置信度（1－α）较______，对应置信区间长度也较_______，此时这⼀估计的精确度_________⽽可信度_____________.σ是否已知，正态总体均值µ的置信区间的中⼼都是7、⽆论总体⽅差2_________________.8、假设检验中统计推断的唯⼀依据是样本信息．样本信息的不完备性和随机性，决定了判断结果有错误是不可避免的．这种错误判断有两种可能：第⼀类错误为弃真错误，显著⽔平α就是犯这类错误的概率；第⼆类为取伪错误，记犯这类错误的概率为β. 则关系式α＋β＝1是________________(正确、错误)的.9、假设检验中做出判断的根据是______________________________________________.10、对于单正态总体，当均值µ已知时，对总体⽅差 2σ的假设检验⽤统计量及分布为__________________________________.⼆、简答题（每⼩题2分，共2×10＝10分）.1、若临界概率α＝0.05，求临界值2αu .答：2、若临界概率α＝0.01，⾃由度k ＝14，求临界值)1401.0(2；χ.答：3、若临界概率α＝0.05，⾃由度k ＝10，求临界值)1005.0(；t . 答：5、设1ξ，2ξ，…，n ξ是ξ的样本，且ξ～ N(µ,2σ)，试求：E ξ、D ξ、E 2*S .答：6、对于总体ξ有E ξ＝µ，D ξ＝2σ，1ξ，2ξ，3ξ是ξ的样本，下列⽆偏估计量中哪⼀个最有效？1?µ＝1ξ，2?µ＝1(31ξ＋2ξ＋3ξ）答：7、设总体ξ服从⼆项分布b(n ，p )，p 为待估参数，),,,(21n ξξξ为ξ的⼀个样本，求p 的矩估计量. 答：8、假设初⽣婴⼉的体重服从正态分布,随机抽取12名初⽣男婴,测得其体重为(单位:g):2950，2520，3000，3000，3000，3160，3560，3320，2880，2600，3400，2540. 当以95%的置信度求初⽣男婴的平均体重的置信区间时，应该选⽤什么统计量？答：9、某种电⼦元件，要求使⽤寿命不得低于1000 h .现从⼀批这种元件中随机抽取25 件，测其寿命，算得其平均寿命950 h ，设该元件的寿命ξ～N （µ，1002），在α＝0.05的检验⽔平下，要确定这批元件是否合格需⽤什么检验⽅法？答：10、某卷烟⼚⽣产两种⾹烟，现分别对两种烟的尼古丁含量作6次测量，结果为甲⼚：25 28 23 26 29 22 ⼄⼚：28 23 30 35 21 27若⾹烟中尼古丁含量服从正态分布，且⽅差相等，要判断这两种⾹烟中尼古丁含量有⽆显著差异（α＝0.05），应该使⽤什么检验⽅法?答：三、应⽤题（每⼩题10分，共6×8＝48分）1、设总体ξ服从泊松分布，即分布列为P(ξ＝m)＝λλ-e m m!，λ＞0为参数，m ＝1,2，…，试求样本(1ξ，2ξ，…，n ξ)的联合分布列.2、设总体ξ服从指数分布，分布密度为)(x p ＝??λ>0为待估参数，n x x x ,,,21 为ξ的⼀个观察值，求λ的最⼤似然估计值.3、已知某⼚⽣产的电⼦零件的长度ξ～N （12.5，2σ），从某天⽣产的零件中随机抽取4个，测得长度为（单位：mm ）12.6 13.4 12.8 13.2，求2σ的置信度为0.95的置信区间.4、已知某种⽊材横纹抗压⼒的实验值ξ～N （µ，2σ），对10个试件作横纹抗压⼒试验，得数据如下(单位：公⽄/平⽅厘⽶)：578 572 570 568 572 570 570 596 584 572.试对2σ进⾏区间估计(α＝0.05).5、已知舞阳钢铁公司的铁⽔含碳量在正常情况下服从正态分布N(4.53，0.1082)，某⽇随机测定了9炉铁⽔，含碳量如下：4.43 4.50 4.58 4.42 4.47 4.60 4.53 4.46 4.42 若已知总体⽅差⽆变化，能否认为该⽇⽣产的铁⽔的平均含碳量仍为4.53（α＝0.05）?6、已知神马集团⽣产的维尼纶的纤度（纤维的粗细程度）在正常情况下服从正态分布N （1.405，0.0482），某⽇随机测定了5根纤维，纤维度如下： 1.32 1.55 1.36 1.40 1.44 问这天维尼纶纤度波动情况是否正常（α＝0.05）?四、论述题（每⼩题10分，共2×6＝12分）1、假设检验的基本原理是什么？2、请你谈谈学习数理统计的⽬的及⽅法？长沙理⼯⼤学模拟试卷第⼋套⼀、填空题（每⼩题2分，共2×10＝20分）. 1、离散程度.2、S 2＝2*1S n n -.3、期望；⽅差.4、似然.5、点估计，区间估计.6、⼤，长，降低，升⾼.7、ξ.8、错误.9、⼩概率事件实际不可能发⽣原理.)(σµξ～2χ(n).⼆、简答题（每⼩题2分，共2×10＝10分）.1、2αu ＝025.0u ＝1.96.2、)1401.0(2；χ＝)14(201.0χ＝29.141.3、)1005.0(；t ＝)10(05.0t ＝1.8125 4、)15,1005.0(；F ＝)15,10(05.0F ＝2.54 5、E ξ＝µ,D ξ＝n2σ，E 2S ＝21σn n -，E 2*S ＝2σ.6、2?µ最有效.7、因µ＝E ξ＝np ，所以p ＝n µ. ⼜µ＝ξ，所以 p ?＝n µ＝n ξ. 8、t 检验法. 9、u 检验法. 10、t 检验法.三、应⽤题（每⼩题10分，共4×12＝48分）1、解设(1x ，2x ，…，n x )为(1ξ，2ξ，…，n ξ)的任⼀组样本值，则样本(1ξ，2ξ，…，n ξ)的联合分布列为P(1ξ=1x ，2ξ=2x ，…，n ξ=n x )＝∏=ni 1P(iξ=iλλ-e x i xi!＝λλn ni i x e x ni i-=∏∑=1!1.2、解由L );,,,(21θn x x x ＝∏=ni i x P i 1);(θξ知，λ的似然函数为L );,,,(21θn x x x ＝∏=-ni x ie 1)(λλ＝∑-=ni ix ne1λλ.相应的对数似然函数为lnL );,,,(21θn x x x ＝两边对λ求导，并令⼀阶导数等于0可得∑=-ni ix n 1λ＝0，解之得，λ的最⼤似然估计值为λ? ＝∑=ni ixn1＝x 1.3、解因∑=-412)(i iµξ＝(12.6－12.5)2＋(13.4－12.5)2＋(12.8－12.5)2＋(13.2－12.5)2＝1.4.⼜ 1－α＝0.95，α＝0.05，查附表3得22αχ＝2025.0χ(4)＝11.143，221αχ-＝2975.0χ(4)＝0.484.故置信度为0.95的置信区间为（143.114.1，484.045、解设该⽇⽣产的铁⽔含碳量ξ～N （µ，2σ），已知σ＝ 0.108, n ＝9，则待检假设为Ho ：µ＝4.53, H 1：µ≠4.53. 当Ho 成⽴时，有统计量u ＝9/108.053.4-ξ～N （0，1）对于给定显著⽔平α＝0.05，查标准正态分布函数数值表（附表2）得2αu ＝1.96，使得P （|u|>1.96）＝0.05.由样本观察值计算得x ＝4.49，于是有 |u|＝|9/108.053.449.4-|＝1.11＜1.96，因⼩概率事件没有发⽣，故接受Ho ，即在显著⽔平α＝0.05下，可认为该⽇⽣产的铁⽔的平均含碳量仍为4.53.6、解设该⽇⽣产的维尼纶的纤度ξ～N （µ，2σ），已知µ＝1.405，σ＝0.048, n ＝5，则待检假设为Ho ：2σ＝0.0482，H 1：2σ≠0.0482.当Ho 成⽴时，有统计量2χ＝∑=-5122048.0)405.1(i i ξ～2χ(5).对于给定显著⽔平α＝0.05，查2χ分布临界值表（附表3）得22αχ＝12.833和221αχ＞12.833）＝2α，P （2χ＜0.83)＝2α.由样本观察值计算2χ得，2χ＝13.683. 于是有2χ＝13.683＞12.833因⼩概率事件发⽣，故拒绝Ho ，即在显著⽔平α＝0.05下，可认为该⽇⽣产的维尼纶的纤度的均⽅差不正常.四、论述题（每⼩题10分，共2×6＝12分） 1、略. 2、略.长沙理⼯⼤学模拟试卷第九套概率论与数理统计试卷⼀、填空题（每⼩题2分，共2×10＝20分）.1、在进⾏抽样时，样本的选取必须是随机的，即总体中每个个体都有同等机会被选⼊样本. 因此，抽取样本1ξ，2ξ，…，n ξ，要求满⾜下列两个特性：1）_________；2）_________. 具备这两个特性的样本称为简单随机样本，简称样本.2、假设1x ，2x ，…，n x 是样本1ξ，2ξ，…，n ξ的⼀个样本值或观测值，则样本均值x 表⽰样本值的集中位置或平均⽔平，样本⽅差S 2和样本修正⽅差S *2表⽰样本值对于均值x 的__________________.3、样本⽅差S 2和样本修正⽅差S *2之间的关系为__________________.4、矩估计法由英国统计学家⽪尔逊（Pearson ）于1894年提出，它简便易⾏，性质良好，⼀直沿⽤⾄今. 其基本思想是：以样本平均值（⼀阶原点矩）ξ作为相应总体ξ的____________________；以样本⽅差（⼆阶中⼼矩）2S 或者以样本修正⽅差2*S 作为相应总体ξ的___________________________.5、θ?具有⽆偏性的意义是：θ?取值因随机性⽽偏离θ的真值，但_________________即没有系统的偏差.6、设1?θ和2?θ都是⽆偏估计量，如果________________，则称1?θ⽐2?θ有效.7、在确定的样本点上，置信区间的长度与事先给定的信度α直接有关. ⼀般来讲，信度α较⼤，其置信度（1－α）较⼩，对应置信区间长度也较短，此时这⼀估计的精确度升⾼⽽可信度降低；相反地，信度α较⼩，其置信度（1－α）较______，对应置信区间长度也较_______，此时这⼀估计的精确度_________⽽可信度_____________.8、假设检验中统计推断的唯⼀依据是样本信息．样本信息的不完备性和随机性，决定了判断结果有错误是不可避免的．这种错误判断有两种可能：第⼀类错误为__________________，第⼆类为__________________.9、常⽤的假设检验⽅法有四种，分别为1）__________________、2）__________________、3）__________________、3）__________________.10、对于单正态总体，当均值µ已知时，对总体⽅差 2σ的假设检验⽤统计量及分布为____________________________________.⼆、简答题（每⼩题2分，共2×10＝10分）.1、若α＝0.05，求2αu .答：3、若α＝0.05，k ＝10，求)1005.0(；t . 答：4、若α＝0.05＜0.5，k 1＝10，k 2＝15，求)15,1005.0(；F . 答：5、设1ξ，2ξ，…，n ξ是ξ的样本，且ξ～ N(µ,2σ)，试求：E ξ、D ξ、E 2*S .答：6、对于总体ξ有E ξ＝µ，D ξ＝2σ，1ξ，2ξ，3ξ是ξ的样本，下列统计量中哪⼀个最有效？1?µ＝1ξ，2?µ＝134ξ－231ξ，3?µ＝1(31ξ＋2ξ＋3ξ）答：7、设总体ξ服从⼆项分布b(n ，p )，p 为待估参数，),,,(21n ξξξ为ξ的⼀个样本，求p 的矩估计量. 答：8、已知⼀批元件的长度测量误差ξ服从N （µ，2σ），µ，2σ为未知参数，现从总体ξ中抽出⼀个容量是6的样本值-1.20，-0.85，-0.30，0.45，0.82，0.12，σ的最⼤似然估计值.求µ，2答：9、已知洛阳轴承⼚⽣产的滚珠直径ξ～N（µ，2σ），其中2σ为已知，µ为待估参数. 从某天⽣产的滚珠中随机抽取⼀个样本1ξ，2ξ，…，nξ，对于事先给定的信度α，试写出总体均值µ的置信区间.答：10、已知洛阳轴承⼚⽣产的滚珠直径ξ～N（µ，2σ），其中2σ为未知知，µ为待估参数. 从某天⽣产的滚珠中随机抽取⼀个样本1ξ，2ξ，…，nξ，对于事先给定的信度α，试写出总体均值µ的置信区间.答：三、应⽤题（每⼩题10分，共4×12＝48分）σ的置信度为0.95的置信区间.求22、已知某种⽊材横纹抗压⼒的实验值ξ～N（µ，2σ），对10个试件作横纹抗压⼒试验，得数据如下(单位：公⽄/平⽅厘⽶)：578 572 570 568 572 570 570 596 584 572.σ进⾏区间估计(α＝0.05).试对23、已知某炼铁⼚的铁⽔含碳量在正常情况下服从正态分布N(4.53，0.1082)，某⽇随机测定了9炉铁⽔，含碳量如下：4.43 4.50 4.58 4.42 4.47 4.60 4.53 4.46 4.42若已知总体⽅差⽆变化，能否认为该⽇⽣产的铁⽔的平均含碳量仍为4.53（α＝0.05）?4、已知某涤纶⼚⽣产的维尼纶的纤度（纤维的粗细程度）在正常情况下服从正态分布N（1.405，0.0482），某⽇随机测定了5根纤维，纤维度如下：1.32 1.55 1.36 1.40 1.44问这天维尼纶纤度总体的均⽅差是否正常（α＝0.05）?四、论述题（每⼩题10分，共2×6＝12分）1、假设检验的基本原理是什么？2、请你谈谈学习数理统计的意义？长沙理⼯⼤学模拟试卷第九套⼀、填空题（每⼩题2分，共2×10＝20分）. 1、1）独⽴性等；2）代表性. 2、离散程度.3、S2＝2*1S n n -.4、期望；⽅差.5、E θ?＝θ.6、D 1?θ＜D 2?θ.7、⼤，长，降低，升⾼. 8、“弃真”，“取伪”.9、1）U 检验法、2）t 检验法、3）2χ检验法、3）F 检验法.10、2χ＝∑=-ni i 122⼆、简答题（每⼩题2分，共2×10＝10分）.1、2αu ＝025.0u ＝1.96.2、)1401.0(2；χ＝)14(201.0χ＝29.141.3、)1005.0(；t ＝)10(05.0t ＝1.8125 4、)15,1005.0(；F ＝)15,10(05.0F ＝2.54 5、E ξ＝µ,D ξ＝n2σ，E 2S ＝21σn n -，E 2*S ＝2σ.6、3?µ最有效.7、因µ＝E ξ＝np ，所以p ＝n µ. ⼜µ＝ξ，所以 p ?＝n µ＝n ξ. 8、µ≈ξ＝61[(-1.20)＋(-0.85)＋(-0.30)＋0.45＋0.82＋0.12]＝－0.16. 2σ≈2S ＝61[(-1.20+0.16)2＋(-0.85+0.16)2＋(-0.30+0.16)2＋(0.45+0.16)2＋(0.82+0.16)2＋(0.12+0.16)2]＝0.4980.9、（ξ2ασu n-，ξ＋)2ασu n.10、（ξnS t 2*2α-，ξ＋)2*2nS t α.三、应⽤题（每⼩题10分，共4×12＝48分） 1、解因∑=-412)(i iµξ＝(12.6－12.5)2＋(13.4－12.5)2＋(12.8－12.5)2＋(13.2－12.5)2＝1.4.⼜ 1－α＝0.95，α＝0.05，查附表3得22αχ＝2025.0χ(4)＝11.143，221αχ-＝2975.0χ(4)＝0.484.故置信度为0.95的置信区间为（143.114.1，484.04.1），即（0.13，2.89）.2、解（35.83，252.43）.3、解设该⽇⽣产的铁⽔含碳量ξ～N （µ，2σ），已知σ＝ 0.108, n ＝9，则待检假设为Ho ：µ＝4.53, H 1：µ≠4.53. 当Ho 成⽴时，有统计量u ＝9/108.053.4-ξ～N （0，1）对于给定显著⽔平α＝0.05，查标准正态分布函数数值表（附表2）得2αu ＝1.96，使得P （|u|>1.96）＝0.05.由样本观察值计算得x ＝4.49，于是有|u|＝|9/108.053.449.4-|＝1.11＜1.96，因⼩概率事件没有发⽣，故接受Ho ，即在显著⽔平α＝0.05下，可认为该⽇⽣产的铁⽔的平均含碳量仍为4.53.4、解设该⽇⽣产的维尼纶的纤度ξ～N （µ，2σ），已知µ＝1.405，σ＝0.048, n ＝5，则待检假设为Ho ：2σ＝0.0482，H 1：2σ≠0.0482.当Ho 成⽴时，有统计量2χ＝∑=-5122048.0)405.1(i i ξ～2χ(5）.对于给定显著⽔平α＝0.05，查2χ分布临界值表（附表3）得22αχ＝12.833和221αχ-＝0.83使得P （2χ＞12.833）＝2α，P （2χ＜0.83)＝2α.由样本观察值计算2χ得，2χ＝13.683. 于是有2χ＝13.683＞12.833因⼩概率事件发⽣，故拒绝Ho ，即在显著⽔平α＝0.05下，可认为该⽇⽣产的维尼纶的纤度的均⽅差不正常.四、论述题（每⼩题10分，共2×6＝12分）1、略. 2、略。

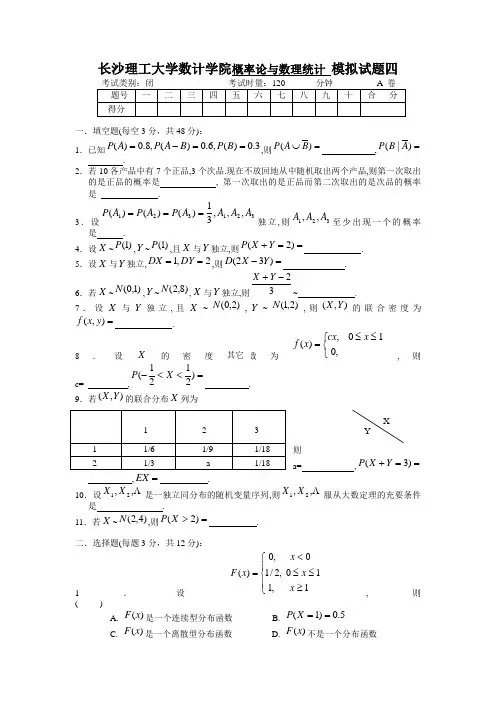
长沙理工大学数计学院概率论与数理统计 模拟试题四一．填空题(每空3分，共48分)：1．已知3.0)(,6.0)(,8.0)(==-=B P B A P A P ,则=⋃)(B A P ,=)|(A B P .2．若10各产品中有7个正品,3个次品.现在不放回地从中随机取出两个产品,则第一次取出的是正品的概率是 , 第一次取出的是正品而第二次取出的是次品的概率是 .3．设321321,,,31)()()(A A A A P A P A P ===独立,则321,,A A A 至少出现一个的概率是 .4．设X ~)1(P ,Y ~)1(P ,且X 与Y 独立,则==+)2(Y X P . 5．设X 与Y 独立,2,1==DY DX ,则=-)32(Y X D .6．若X ~)1,0(N ,Y ~)8,2(N ,X 与Y 独立,则32-+Y X ~ .7．设X 与Y 独立,且X ~)2,0(N ,Y ~)2,1(N ,则),(Y X 的联合密度为=),(y x f .8．设X的密度函数为⎩⎨⎧≤≤=,010,)(x cx x f ,则c= ,=<<-)2121(X P .9．若),(Y X 的联合分布X 列为则a= ,==+)3(Y X P,=EX .10．设 ,,21X X 是一独立同分布的随机变量序列,则 ,,21X X 服从大数定理的充要条件是 . 11．若X ~)4,2(N ,则=>)2(X P .二．选择题(每题3分，共12分)：1．设⎪⎩⎪⎨⎧≥≤≤<=1,110,2/10,0)(x x x x F ,则( )A. )(x F 是一个连续型分布函数B. 5.0)1(==X PC. )(x F 是一个离散型分布函数D. )(x F 不是一个分布函数其它 XY2．设B A ,为两事件,且1)(0<<A P ,则下列命题中不成立的是 ( )A .B A ,独立)()()(B P A P AB P =⇔ B. B A ,独立)()|(B P A B P =⇔C. B A ,独立0)(=⇔AB PD. B A ,独立)|()|(A B P A B P =⇔3．设随机变量X 的密度函数为)(x f ,且满足),(),()(+∞-∞∈-=x x f x f ,)(x F 为X 的分布函数,则对任意的实数x 有( ) A . )(1)(x F x F -=- B. )(2/1)(x F x F -=-C. )()(x F x F =-D. 1)(2)(-=-x F x F4．设2,1==DX EX ,则( )A. 2/1)2|(|≥>X PB. 2/1)2|1(|≥≥-X PC. 2/1)2|1(|≤<-X PD. 2/1)2|1(|≤≥-X P三．一仓库有10箱同种规格的产品,其中由甲,乙,丙三厂生产的分别为5箱,3箱,2箱,三厂产品的次品率依次为0.1,0.2,0.3,从这10箱产品中任取一箱,再从这箱中任取一件,取得正品,求该件产品由甲厂生产的概率. (8分)四．某人有12粒弹子,其中有2粒为绿色的.今从中不放回地取两次,每次取一粒,Y X ,分别表示第一次,第二次取中绿色弹子的粒数,求EXY . ( 7分)五．设随机向量),(Y X 的联合密度函数为:⎪⎩⎪⎨⎧≤≤≤≤+=,020,10,31),(2y x xy x y x f1)Y X ,是否独立; 2)求)1(>+Y X P ; 3)求)21|1(=<X Y P . (12分)六．在一家保险公司里有10000人投保,每人每年付12元保险费.在一年内一个人死亡的概率为0.006,死亡时其家属可从保险公司得到1000元赔偿.求该保险公司一年的利润不少于60000元的概率. （6分）七．设甲乙两车间加工同一种产品，其产品的尺寸分别为随机变量为ηξ,,且),(~),,(~222211σμησμξN N ，今从它们的产品中分别抽取若干进行检测，测得数据如下：397.4,50.21,7,216.2,93.20,82222111======s y n s x n （查表：12.5)7,6(,70.5)6,7(025.0025.0==F F ）求21μμ-的置信度为90％的置信区间。

长沙理工大学高等数学试题及答案一、单项选择题（本大题共5 小题，每小题2 分，共 10 分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设 f(x)=lnx，且函数 (x) 的反函数1(x)= 2(x+1) ，则 f (x)（）x-1et2 dt2． limetx（）x 01 cos xA ． 0 B． 1 C ．-1D ．3．设 y f (x 0x)f ( x 0 ) 且函数 f (x) 在 x x 0 处可导，则必有（）4．设函数 f(x)=2x 2 , x 1，则 f(x) 在点 x=1处（）3x1,x 1A. 不连续B.连续但左、右导数不存在C.连续但不可导D.可导5．设 xf(x)dx=e-x2C ，则 f(x)= （）二、填空题（本大题共 10 小题，每空 3 分，共 30 分）请在每小题的空格中填上正确答案。

错填、不填均无分。

6. 设函数 f(x) 在区间 [0 ，1] 上有定义，则函数 f(x+1)+f(x-1) 的定义域是 __________.7．lim44a aqaq2L aqnq 1 _________n8． lim arctan x_________xx9. 已知某产品产量为 g 时，总成本是 C(g)=9+g 2，则生产 100 件产品时的边际成本 MC g 100 __80010. 函数 f (x) x 3 2x 在区间 [0 ，1] 上满足拉格朗日中值定理的点ξ是 _________.11. 函数 y 2x 39x 2 12x 9 的单调减少区间是 ___________.12. 微分方程 xy ' y 1 x 3 的通解是 ___________. 13. 2ln 2dt, 则 a ___________.设e ta1614. 设 zcos 2 x 则 dz= _______.y15. 设 D (x, y) 0 x 1,0 y 1 ，则 xe 2 y dxdy _____________.D三、计算题（一） （本大题共 5 小题，每小题 5 分，共 25 分）x16. 设 y1 ，求 dy.x17. 求极限 lim ln cot xx 0ln x18. 求不定积分1dx.5x 1ln 5x 119. 计算定积分 I=aa 2 x 2dx.20. 设方程 x 2 y 2xz e z 1确定隐函数 z=z(x,y) ，求 z 'x , z 'y 。

P ( A B ) P ( AB ) 1 P ( AB ) 0.6
P ( A B ) P ( AB ) 1 P ( AB ) 0.7
P ( AB ) P ( B AB ) P ( B ) P ( AB ) 0.2 P ( A AB ) P ( A) P ( AB ) 0.9
数计院梁小林（2014 年 10 月）
容易算出
() 122 , ( A)
( A) 221 () 288
102 112 2
所以 P ( A) ( x, y ) | y x ，区域图如下：
容易算出 ( B ) 0 所以 P ( B ) 0 但是 B
第七题 因为 P ( AB ) P ( A) P ( A B )) 0.7 0.3 0.4 所以 P ( AB ) 1 P ( AB )) 0.6
练习 1.3 条件概率、全概率公式
第一题 1. P ( AB ) P ( B | A) P ( A) a c
由条件概率：
P ( A1 B ) P ( B | A1 ) P ( A1 ) 0.06 12 P( B) P( B) 0.105 21 P ( A2 B ) P ( B | A2 ) P ( A2 ) 0.02 4 P ( A2 | B ) P( B) P( B) 0.105 21 P ( A3 B ) P ( B | A3 ) P ( A3 ) 0.025 5 P ( A3 | B ) P( B) P( B) 0.105 21 P ( A1 | B )
易得此产品最可能是第一车间生产的 第四题 解：设 A {人患有肝癌}
B {人被此法诊断为肝癌患者}

长沙理工大学模拟试卷第七套概率论与数理统计试卷: 班级: 学号: 得分: 一．判断题〔10分，每题2分〕1. 在古典概型的随机试验中，0)(=A P 当且仅当A 是不可能事件 ( )2．连续型随机变量的密度函数)(x f 与其分布函数)(x F 相互唯一确定 ( )3．假设随机变量X 与Y 独立，且都服从1.0=p 的 (0，1) 分布，则Y X =( ) 4．设X 为离散型随机变量, 且存在正数k 使得0)(=>k X P ，则X 的数学期望)(X E 未必存在( )5．在一个确定的假设检验中，当样本容量确定时, 犯第一类错误的概率与犯第二类错误的概率不能同时减少 ( ) 二．选择题〔15分，每题3分〕1. 设每次试验成功的概率为)10(<<p p ，重复进行试验直到第n 次才取得)1(n r r ≤≤次成功的概率为 .(a) r n r r n p p C ----)1(11； (b) r n r r n p p C --)1(； (c) 1111)1(+-----r n r r n p p C ； (d) r n r p p --)1(.2. 离散型随机变量X 的分布函数为)(x F ，则==)(k x X P . (ａ) )(1k k x X x P ≤≤-； (ｂ) )()(11-+-k k x F x F ； (ｃ) )(11+-<<k k x X x P ； (ｄ) )()(1--k k x F x F .3. 设随机变量X 服从指数分布，则随机变量)2003,(max X Y =的分布函 数 .(ａ) 是连续函数； (ｂ) 恰好有一个间断点； (ｃ) 是阶梯函数； (ｄ) 至少有两个间断点.4. 设随机变量),(Y X 的方差,1)(,4)(==Y D X D 相关系数,6.0=XY ρ则方差=-)23(Y X D . (ａ) 40； (ｂ) 34； (ｃ) 25.6； (ｄ) 17.65. 设),,,(21n X X X 为总体)2,1(2N 的一个样本，X 为样本均值，则以下结论中正确的选项是 .(ａ) )(~/21n t n X -； (ｂ) )1,(~)1(4112n F X ni i ∑=-；(ｃ) )1,0(~/21N n X -； (ｄ) )(~)1(41212n X ni i χ∑=-. 二. 填空题〔28分，每题4分〕 . 连续两次不放回地从中任取一个, 则第二次才取到正品的概率为2. 设连续随机变量的密度函数为)(x f ，则随机变量Xe Y 3=的概率密度函数为=)(y f Y3. 设X 为总体)4,3(~N X 中抽取的样本(4321,,,X X X X )的均值, 则)51(<<-X P ＝ . 4. 设二维随机变量),(Y X 的联合密度函数为⎩⎨⎧<<<=他其,0;10,,1),(x x y y x f则条件密度函数为,当 时 ,=)(x y f X Y5. 设)(~m t X ,则随机变量2X Y =服从的分布为 ( 需写出自由度 )6. 设某种保险丝熔化时间),(~2σμN X 〔单位：秒〕，取16=n 的样本，得样本均值和方差分别为36.0,152==S X ，则μ的置信度为95%的单侧 置信区间上限为7. 设X 的分布律为X 1 2 3P 2θ )1(2θθ- 2)1(θ-已知一个样本值)1,2,1(),,(321=x x x ，则参数的极大似然估计值 为三. 计算题〔40分，每题8分〕1. 已知一批产品中96 %是合格品. 检查产品时，一合格品被误认为是次品的 概率是0.02；一次品被误认为是合格品的概率是0.05．求在被检查后认 为是合格品的产品确实是合格品的概率2．设随机变量X 与Y 相互独立，X ，Y 分别服从参数为)(,μλμλ≠的指数 分布，试求Y X Z 23+=的密度函数)(z f Z .3．某商店出售某种贵重商品. 根据经验，该商品每周销售量服从参数为1=λ 的泊松分布. 假定各周的销售量是相互独立的. 用中心极限定理计算该商店一年内〔52周〕售出该商品件数在50件到70件之间的概率.4. 总体),(~2σμN X ，),,,(21n X X X 为总体X 的一个样本.求常数 k , 使∑=-ni i XX k 1为σ 的无偏估计量.5．〔1〕 根据长期的经验，某工厂生产的特种金属丝的折断力),(~2σμN X〔单位：kg 〕. 已知8=σkg ， 现从该厂生产的一大批特种金属丝中随机抽取10个样品，测得样本均值2.575=x kg . 问这批特种金属丝的 平均折断力可否认为是570 kg ？ 〔%5=α〕〔2〕 已知维尼纶纤度在正常条件下服从正态分布)048.0,(2μN . 某日抽取 5个样品，测得其纤度为: 1.31， 1.55， 1.34， 1.40， 1.45 .问 这天的纤度的总体方差是否正常？试用%10=α作假设检验. 四. 证明题〔7分〕设随机变量Z Y X ,,相互独立且服从同一贝努利分布),1(p B . 试证明随机变量Y X +与Z 相互独立.附表： 标准正态分布数值表 2χ分布数值表 t 分布数值表6103.0)28.0(=Φ 488.9)4(205.0=χ 1315.2)15(025.0=t975.0)96.1(=Φ 711.0)4(295.0=χ 7531.1)15(05.0=t 9772.0)0.2(=Φ 071.11)5(205.0=χ 1199.2)16(025.0=t9938.0)5.2(=Φ 145.1)5(295.0=χ 7459.1)16(05.0=t长沙理工大学模拟试卷第七套概率论与数理统计试卷答案一. 判断题〔10分，每题2分〕 是 非 非 非 是 . 二. 选择题〔15分，每题3分〕 〔ａ〕〔ｄ〕〔ｂ〕〔ｃ〕〔ｄ〕. 三. 填空题〔28分，每题4分〕1.1/22 ；2.⎩⎨⎧≤>=000)])3/[ln()(1y y y f y f y Y ； 3.0.9772 ； 4. 当10<<x 时⎩⎨⎧<<-=他其0)2/(1)(xy x x x y f X Y ； 5. ),1(m F 6. 上限为 15.263 . 7. 5 / 6 . 四. 计算题〔40分，每题8分〕1. A 被查后认为是合格品的事件，B 抽查的产品为合格品的事件. (2分)9428.005.004.098.096.0)()()()()(=⨯+⨯=+=B A P B P B A P B P A P ， (4分).998.09428.0/9408.0)(/)()()(===A P B A P B P A B P (2分) 2. ⎩⎨⎧>=-其他00)(x e x f x X λλ⎩⎨⎧>=-其他00)(y e y f y Y μμ (1分) 0≤z 时，0)(=z F Z ，从而 0)(=z f Z ； (1分)0≤z 时，⎰∞+-∞-=dxx z f x f z f Y X Z ]2/)3[()()(21 (2分))(232/3/3/0]2/)[(21z z z x z x e e dx e μλμλλμλμλμ-------==⎰(2分)所以⎪⎩⎪⎨⎧≤>--=--0,00),(23)(2/3/z z e e z f z z Z μλλμλμ[⎪⎩⎪⎨⎧≤>--=--0,00),(32)(3/2/z z e e z f z z Z μλλμλμ] (2分) 3. 设 i X 为第i 周的销售量, 52,,2,1 =i i X )1(~P (1分)则一年的销售量为 ∑==521i iX Y ，52)(=Y E , 52)(=Y D . (2分)由独立同分布的中心极限定理，所求概率为1522521852185252522)7050(-⎪⎪⎭⎫⎝⎛Φ+⎪⎪⎭⎫ ⎝⎛Φ≈⎪⎪⎭⎫ ⎝⎛<-<-=<<Y P Y P (4分) 6041.016103.09938.01)28.0()50.2(=-+=-Φ+Φ=. (1分)4. 注意到5. (1) 要检验的假设为 570:,570:10≠=μμH H (1分)检验用的统计量)1,0(~/0N nX U σμ-=， 拒绝域为 96.1)1(025.02==-≥z n z U α. (2分)96.106.21065.010/85702.5750>==-=U ，落在拒绝域内，故拒绝原假设0H ，即不能认为平均折断力为570 kg . [96.1632.0102.010/92.5695710<==-=U , 落在拒绝域外，故接受原假设0H ，即可以认为平均折断力为571 kg . ] (1分)(2) 要检验的假设为 221220048.0:,048.0:≠=σσH H (1分)[22122079.0:,79.0:≠=σσH H ]检验用的统计量)1(~)(2202512--=∑=n X Xi iχσχ，()n i i X X n X X n X X ---+--=- )1(121)2(1)(,0)(2分σn n X X D X X E i i -=-=-1(10~2⎪⎭⎫ ⎝⎛--σn n N X X i dz e nn z X X E n n z i 2212121|||)(|σσπ--∞+∞-⎰-=-dz e n n z nn z 221201212σσπ--∞+⎰-=)3(122分σπn n -=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-∑∑==ni i ni i X X E k X X k E 11||||σπnn kn 122-=σ令=）分（2)1(2-=n n k π拒绝域为488.9)4()1(205.022==->χχχαn 或711.0)4()1(295.02122==-<-χχχαn (2分)41.1=x [49.1=x ]488.9739.150023.0/0362.020>==χ, 落在拒绝域内，[711.0086.06241.0/0538.020<==χ,落在拒绝域内，] 故拒绝原假设0H ，即认为该天的纤度的总体方差不正常 . (1分) 五、证明题 (7分) 由题设知X 0 1 Y X + 0 1 2P p q P 2q pq 2 2p (2分))0()0()0,0(3==+====+Z P Y X P q Z Y X P ；)1()0()1,0(2==+====+Z P Y X P pq Z Y X P ；)0()1(2)0,1(2==+====+Z P Y X P pq Z Y X P ；)1()1(2)1,1(2==+====+Z P Y X P pq Z Y X P ；)0()2()0,2(2==+====+Z P Y X P pq Z Y X P ；)1()2()1,2(3==+====+Z P Y X P p Z Y X P . 所以 Y X +与Z 相互独立. (5分)。

长沙理工大学高等数学试题及答案一、单项选择题(本大题共５小题,每小题2分，共10分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

１.设f(x)=lnx ，且函数ϕ(x)的反函数1ϕ-2(x+1)(x)=x-1，则[]ϕ=f (x)（ ) ....A B C D x-2x+22-x x+2 ln ln ln ln x+2x-2x+22-x ２.()002lim 1cos t t x x e e dt x -→+-=-⎰( ）A ．0B ．1 C.-1ﻩ D.∞３．设00()()y f x x f x ∆=+∆-且函数()f x 在0x x =处可导,则必有( ）.lim 0.0.0.x A y B y C dy D y dy ∆→∆=∆==∆= 4.设函数,131,1x x x ⎧≤⎨->⎩22x f(x)=,则f(x)在点x=1处( )A.不连续B.连续但左、右导数不存在C.连续但不可导 D ． 可导5．设C +⎰2-x xf(x)dx=e，则f(x)=( ) 2222-x -x -x -x A.xe B.-xe C.2e D.-2e二、填空题(本大题共１0小题，每空3分，共30分)请在每小题的空格中填上正确答案。

错填、不填均无分。

6．设函数f(x)在区间[0,１]上有定义，则函数f(x ＋14)＋f （ｘ-14）的定义域是_＿＿___＿__＿. ７．()()2lim 1_________n n a aq aq aq q →∞++++<= 8.arctan lim _________x x x→∞= ９.已知某产品产量为g 时,总成本是2g C(g)=9+800,则生产100件产品时的边际成本100__g ==MC 10.函数3()2f x x x =+在区间[０，１]上满足拉格朗日中值定理的点ξ是__＿______.１１.函数3229129y x x x =-+-的单调减少区间是______＿＿__＿.1２.微分方程3'1xy y x -=+的通解是_____＿__＿__.13.设2ln 2,6a a π==⎰则＿__＿___＿___.14．设2cos x z y =则ｄz= ___＿＿＿_. 1５.设{}2(,)01,01y DD x y x y xe dxdy -=≤≤≤≤=⎰⎰，则_＿___＿_＿＿＿___.三、计算题(一）(本大题共5小题,每小题5分，共２５分)16.设1x y x ⎛⎫= ⎪⎝⎭,求dy. １7.求极限0ln cot lim ln x x x+→1８．求不定积分.19.计算定积分I=0.a ⎰ 20.设方程2z x 2e 1y xz -+=确定隐函数ｚ=ｚ(ｘ,y)，求','x y z z 。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载长沙理工大学往届高等数学试题及答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容长沙理工大学高等数学试题及答案一、单项选择题（本大题共5小题，每小题2分，共10分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设，且函数的反函数，则（）2．（）A．0 B．1 C．-1 D．3．设且函数在处可导，则必有（）4．设函数，则在点处（）A.不连续B.连续但左、右导数不存在C.连续但不可导D. 可导5．设，则（）二、填空题（本大题共10小题，每空3分，共30分）请在每小题的空格中填上正确答案。

错填、不填均无分。

6.设函数f(x)在区间[0，1]上有定义，则函数f(x+)+f(x-)的定义域是__________.7．8．9.已知某产品产量为g时，总成本是，则生产100件产品时的边际成本10.函数在区间[0，1]上满足拉格朗日中值定理的点ξ是_________.11.函数的单调减少区间是___________.12.微分方程的通解是___________.13.设___________.14.设则dz= _______.15.设_____________.三、计算题（一）（本大题共5小题，每小题5分，共25分）16.设，求dy.17.求极限18.求不定积分19.计算定积分I=20.设方程确定隐函数z=z(x,y)，求。

四、计算题（二）（本大题共3小题，每小题7分，共21分）21．要做一个容积为v的圆柱形容器，问此圆柱形的底面半径r和高h分别为多少时，所用材料最省？22.计算定积分23.将二次积分化为先对x积分的二次积分并计算其值。