高考数学一轮总复习 10.5 直线、平面垂直的判定及其性质教案 理 新人教A版

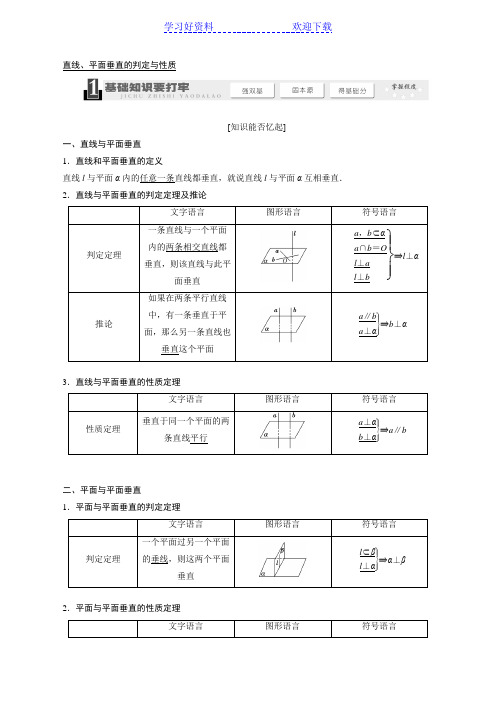
直线、平面垂直的判定与性质ZHI SHI SHU LI 知识梳理 ) 1．直线与平面垂直 (1)直线与平面垂直①定义：若直线l 与平面α内的任意一条直线都垂直，则直线l 与平面α垂直．②判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直(线线垂直⇒线面垂直)．即：a ⊂α，b ⊂α，l ⊥a ，l ⊥b ，a ∩b ＝P ⇒l ⊥α. ③性质定理：垂直于同一个平面的两条直线平行.即：a ⊥α，b ⊥α⇒a ∥b . (2)直线与平面所成的角①定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条斜线和这个平面所成的角．若直线与平面平行或直线在平面内，直线与平面所成角为0，若直线与平面垂直，直线与平面所成角为π2.②线面角θ的范围：θ∈[0，π2]．2．平面与平面垂直 (1)二面角的有关概念①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．②二面角的平面角：以二面角的棱上任意一点为端点，在两个半平面内分别作与棱垂直的射线，则两射线所成的角叫做二面角的平面角． (2)平面与平面垂直①定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直． ②判定定理：一个平面过另一个平面的垂线，则这两个平面垂直．即：a ⊂α，a ⊥β⇒α⊥β. ③性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．即：α⊥β，a ⊂α，α∩β＝b ，a ⊥b ⇒a ⊥β.ZHONG YAO JIE LUN重要结论) 1．若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．2．若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)．3．垂直于同一条直线的两个平面平行．4．一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．SHUANG JI ZI CE双基自测)1．(2019·浙江模拟)已知互相垂直的平面α，β交于直线l.若直线m，n满足m∥α，n⊥β，则(C)A．m∥l B．m∥nC．n⊥l D．m⊥n[解析]由题意知α∩β＝l，所以l⊂β.因为n⊥β，所以n⊥l.故选C．2．(2019·甘肃马营中学月考)若m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题中的真命题是(C)A．若m⊂β，α⊥β，则m⊥αB．若α∩γ＝m，β∩γ＝n，m∥n，则α∥βC．若m⊥β，m∥α，则α⊥βD．若α⊥γ，α⊥β，则β⊥γ[解析]若m⊂β，α⊥β，则m与α的关系可能平行也可能相交或m⊂α，则A为假命题；选项B中，α与β可能平行也可能相交，则B为假命题；选项D中β与γ也可能平行或相交(不一定垂直)，则D为假命题，故选C．3．(2017·全国卷Ⅲ)在正方体ABCD－A1B1C1D1中，E为棱CD的中点，则(C)A．A1E⊥DC1B．A1E⊥BDC．A1E⊥BC1D．A1E⊥AC[解析]由正方体的性质，得A1B1⊥BC1，B1C⊥BC1，所以BC1⊥平面A1B1CD，又A1E⊂平面A1B1CD，所以A1E⊥BC1，故选C．4．(2019·中原名校联考)已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是(C)A．α⊥β且m⊂αB．α⊥β且m∥αC．m∥n且n⊥βD．m⊥n且n∥β[解析]对于选项A，α⊥β且m⊂α，可得m∥β或m与β相交或m⊂β，故A不成立；对于选项B，α⊥β且m∥α，可得m⊂β或m∥β或m与β相交，故B不成立；对于选项C，m∥n 且n⊥β，则m⊥β，故C正确；对于选项D，由m⊥n且n∥β，可得m∥β或m与β相交或m⊂β，故D不成立．故选C．5．已知矩形ABCD，AB＝1，BC＝2，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中(B)A．存在某个位置，使得直线AC与直线BD垂直B．存在某个位置，使得直线AB与直线CD垂直C．存在某个位置，使得直线AD与直线BC垂直D．对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直[解析]对于AB⊥CD，因为BC⊥CD，可得CD⊥平面ACB，因此有CD⊥AC，因为AB＝1，BC＝2，CD＝1，所以AC＝1，所以存在某个位置，使得AB⊥CD．6．(2019·西安一模)在四棱锥P－ABCD中，P A⊥平面ABCD，底面各边都相等，M是PC 上的一动点，当点M满足BM⊥PC时，平面MBD⊥平面PCD．[解析]∵△P AB≌P AD，∴PB＝PD，∴△PDC≌△PBC，当BM⊥PC时，有DM⊥PC，此时PC ⊥平面MBD，∴平面MBD⊥平面PCD．故填BM⊥PC．考点1空间垂直关系的基本问题——自主练透例1(1)已知α，β为两个不同的平面，l为直线，若α⊥β，α∩β＝l，则(D) A．垂直于平面β的平面一定平行于平面αB．垂直于直线l的直线一定垂直于平面αC．垂直于平面β的平面一定平行于直线lD．垂直于直线l的平面一定与平面α，β都垂直(2)(2018·贵阳市监测考试)如图，在三棱锥P－ABC中，不能证明AP⊥BC的条件是(B)A．AP⊥PB，AP⊥PCB．AP⊥PB，BC⊥PBC．平面BPC⊥平面APC，BC⊥PCD．AP⊥平面PBC[解析](1)由面面垂直的判定定理可知，垂直于直线l的平面一定与平面α，β都垂直．故选D．(2)A中，因为AP⊥PB，AP⊥PC，PB∩PC＝P，所以AP⊥平面PBC，又BC⊂平面PBC，所以AP⊥BC，故A能证明AP⊥BC；C中，因为平面BPC⊥平面APC，BC⊥PC，所以BC ⊥平面APC，AP⊂平面APC，所以AP⊥BC，故C能证明AP⊥BC；由A知D能证明AP ⊥BC；B中条件不能判断出AP⊥BC，故选B．名师点拨☞解决空间中线面、面面垂直的问题有以下三种方法：(1)依据相关定理得出结论；(2)结合符合题意的模型(如构造正方体、长方体)作出判断；(3)否定命题时只需举一个反例即可．考点2直线与平面垂直的判定与性质——多维探究角度1线面垂直的判定例2(2018·新课标全国Ⅱ卷)如图，在三棱锥P－ABC中，AB＝BC＝22，P A＝PB＝PC＝AC＝4，O为AC的中点．(1)证明：PO⊥平面ABC；(2)若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．[解析](1)因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2 3.连接OB，因为AB＝BC＝22AC，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知，OP ⊥OB ． 由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC ． (2)作CH ⊥OM ，垂足为H .又由(1)可得OP ⊥CH ，所以CH ⊥平面POM . 故CH 的长为点C 到平面POM 的距离．由题设可知OC ＝12AC ＝2，CM ＝23BC ＝423，∠ACB ＝45°.所以OM ＝253，CH ＝OC ·MC ·sin ∠ACB OM ＝455.所以点C 到平面POM 的距离为455.角度2 线面垂直的性质例3 (2018·山东潍坊模拟)如图，在平行六面体ABCD －A 1B 1C 1D 1中，AB ＝BC ，AA 1＝DA 1，∠ABC ＝120°.(1)证明：AD ⊥BA 1；(2)若AD ＝DA 1＝4，BA 1＝26，求多面体BCD －A 1B 1C 1D 1的体积． [解析](1)证明：取AD 中点O ，连接OB ，OA 1. ∵AA 1＝DA 1，∴AD ⊥OA 1. ∵在▱ABCD 中，∠ABC ＝120°， ∴∠BAD ＝60°.又∵AB ＝BC ，∴AB ＝AD ，∴△ABD 是正三角形， ∴AD ⊥OB ．∵OA 1⊂平面OBA 1，OB ⊂平面OBA 1，OA 1∩OB ＝O ， ∴AD ⊥平面OBA 1.又A 1B ⊂平面OBA 1. ∴AD ⊥BA 1.(2)由题设△A 1AD 与△BAD 都是边长为4的正三角形． ∴A 1O ＝OB ＝2 3.∵A 1B ＝26，∴A 1O 2＋OB 2＝A 1B 2，∴A 1O ⊥OB ． ∵A 1O ⊥AD ，OB ，AD ⊂平面ABCD ，OB ∩AD ＝O ， ∴A 1O ⊥平面ABCD ，∴A 1O 是平行六面体ABCD －A 1B 1C 1D 1的高． 又S ABCD ＝AD ·OB ＝4×23＝83，∴V ＝VABCD －A 1B 1C 1D 1＝S ABCD ·A 1O ＝83×23＝48， V 1＝VA 1－ABD ＝13S △ABD ·A 1O ＝13×12×4×23×23＝8.∴VBCD －A 1B 1C 1D 1＝V －V 1＝40，即多面体BCD －A 1B 1C 1D 1的体积为40.名师点拨 ☞(1)解决直线与平面垂直问题的常用方法：①利用线面垂直的定义；②利用线面垂直的判定定理；③利用线面垂直的性质；④利用面面垂直的判定定理；⑤利用面面垂直的性质． (2)由于“线线垂直”“线面垂直”“面面垂直”之间可以相互转化，因此整个证明过程围绕着“线面垂直”这个核心展开，这是化解空间垂直关系问题难点的技巧所在． 〔变式训练1〕(1)(角度1)如图，在三棱锥P －ABC 中，平面P AB ⊥平面ABC ，AB ＝6，BC ＝23，AC ＝26，D 为线段AB 上的点，且AD ＝2DB ，PD ⊥AC ．①求证：PD ⊥平面ABC ；②若∠P AB ＝π4，求点B 到平面P AC 的距离．(2)(角度2)(2019·新疆乌鲁木齐诊断)在直三棱柱ABC －A 1B 1C 1中，AC ＝BC ＝2，AB ＝AA 1＝2，E 是棱CC 1的中点．(1)求证：A 1B ⊥AE ；(2)求点A 1到平面ABE 的距离．[解析] (1)①连接CD ，据题知AD ＝4，BD ＝2，AC 2＋BC 2＝AB 2， ∴∠ACB ＝90°，∴cos ∠ABC ＝236＝33， ∴CD 2＝22＋(23)2－2×2×23cos ∠ABC ＝8，∴CD ＝22， ∴CD 2＋AD 2＝AC 2，则CD ⊥AB ． ∵平面P AB ⊥平面ABC ， ∴CD ⊥平面P AB ，∴CD ⊥PD ， ∵PD ⊥AC ，AC ∩CD ＝C ， ∴PD ⊥平面ABC ． ②由①知PD ⊥AB ，∵∠P AB ＝π4，∴PD ＝AD ＝4，P A ＝42，在Rt △PCD 中，PC ＝PD 2＋CD 2＝26，∴△P AC 是等腰三角形，∴可求得S △P AC ＝8 2. 设点B 到平面P AC 的距离为d ，由V B －P AC ＝V P －ABC ，得13S △P AC ×d ＝13S △ABC ×PD ，∴d ＝S △ABC ×PDS △P AC＝3.故点B 到平面P AC 的距离为3.(2)①证明：如图，取A 1B 的中点F ，连接AF ，EF .∵三棱柱ABC －A 1B 1C 1是直三棱柱， ∴CC 1⊥A 1C 1，CC 1⊥CB ，又∵E 是CC 1的中点，且A 1C 1＝BC ， ∴A 1E ＝BE ，∴A 1B ⊥EF . 又∵AB ＝AA 1，∴A 1B ⊥AF . 又AF ∩EF ＝F ，∴A 1B ⊥平面AEF . 又AE ⊂平面AEF ，∴A 1B ⊥AE .②V 三棱锥A 1－ABE ＝V 三棱锥B －A 1AE ＝13×12×2×2×2＝23，设A 1到平面ABE 的距离为h ， 则13S △ABE ·h ＝23， 由已知得AE ＝BE ＝3，∴S △ABE ＝12×2×2＝2，∴h ＝ 2.考点3 证明空间两个平面垂直——师生共研例4 (2019·黑龙江模拟)在三棱柱ABC －A 1B 1C 1中，侧棱与底面垂直，∠ABC ＝90°，AB ＝BC ＝BB 1＝2，M ，N 分别是AB ，A 1C 的中点．(1)求证：MN∥平面BCC1B1；(2)求证：平面MAC1⊥平面A1B1C．[证明](1)连接BC1，AC1.由题意，在三棱柱ABC－A1B1C1中，N是A1C的中点，∴N是AC1的中点．在△ABC1中，∵M，N是AB，AC1的中点，∴MN∥BC1.又∵MN⊄平面BCC1B1，BC1⊂平面BCC1B1，∴MN∥平面BCC1B1.(2)∵三棱柱ABC－A1B1C1中，侧棱与底面垂直，∴四边形BCC1B1是正方形，∴BC1⊥B1C，∴MN⊥B1C．连接A1M，CM，则△AMA1≌△BMC，∴A1M＝CM.∵N是A1C的中点，∴MN⊥A1C．∵A1C∩B1C＝C，∴MN⊥平面A1B1C．∵MN⊂平面MAC1，∴平面MAC1⊥平面A1B1C．名师点拨☞(1)证明面面垂直的常用方法：①利用面面垂直的定义；②利用面面垂直的判定定理，转化为从现有直线中(或作辅助线)寻找平面的垂线，即证明线面垂直．(2)两个平面垂直问题，通常是通过“线线垂直→线面垂直→面面垂直”的过程来实现的．〔变式训练2〕如图，三棱柱ABC－A1B1C1中，侧面BB1C1C是边长为2且∠CBB1＝60°的菱形，AB＝AC1.(1)证明：平面AB1C⊥平面BB1C1C；(2)若AB⊥B1C，AB＝BC，求点B到平面A1B1C1的距离．[解析](1)如图，连接BC1交B1C于点O，连接AO.∵侧面BB1C1C为菱形，∴B1C⊥BC1，∵AB＝AC1，O为BC1的中点，∴AO⊥BC1，又B1C∩AO＝O，∴BC1⊥平面AB1C，又BC1⊂平面BB1C1C，∴平面AB1C⊥平面BB1C1C．(2)∵AB⊥B1C，BO⊥B1C，AB∩BO＝B，∴B1C⊥平面ABO，又AO⊂平面ABO，∴AO⊥B1C，又AO⊥BC1，BC1∩B1C＝O，∵AO⊥平面BB1C1C．∵菱形BB1C1C的边长为2且∠CBB1＝60°，∴BO＝3，∵AB＝BC＝2，∴AO＝1.又CO＝1，∴AC＝2，S△ABC＝S△A1B1C1＝72.连接A1B，设点B到平面A1B1C1的距离为h，由V三棱锥B－A1B1C1＝V三棱锥A1－BB1C1＝V三棱锥A－BB1C1，得1 3×72×h＝13×12×2×2×32×1，∴h＝2217，即点B到平面A1B1C1的距离为2217.立体几何中的折叠问题例5 如图1，在直角梯形ABCD 中，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝12AB ＝2，E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直，如图2.在图2所示的几何体D －ABC 中：(1)求证：BC ⊥平面ACD ；(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积．[解析] (1)∵AC ＝AD 2＋CD 2＝22，∠BAC ＝∠ACD ＝45°，AB ＝4，∴在△ABC 中，BC 2＝AC 2＋AB 2－2AC ×AB ×cos45°＝8，∴AB 2＝AC 2＋BC 2＝16，∴AC ⊥BC ，∵平面ACD ⊥平面ABC ，平面ACD ∩平面ABC ＝AC ，∴BC ⊥平面ACD ．(2)∵AD ∥平面BEF ，AD ⊂平面ACD ，平面ACD ∩平面BEF ＝EF ，∴AD ∥EF ，∵E 为AC 的中点，∴EF 为△ACD 的中位线，由(1)知，V F －BCE ＝V B －CEF ＝13×S △CEF ×BC ， S △CEF ＝14S △ACD ＝14×12×2×2＝12， ∴V F －BCE ＝13×12×22＝23.名师点拨 ☞证明折叠问题中的平行与垂直，关键是分清折叠前后图形的位置和数量关系的变与不变．一般地，折叠前位于“折痕”同侧的点、线间的位置和数量关系折叠后不变，而折叠前位于“折痕”两侧的点、线间的位置关系折叠后会发生变化．对于不变的关系可在平面图形中处理，而对于变化的关系则要在立体图形中解决．〔变式训练3〕(2018·湖北八市联考)如图，在Rt△ABC中，AB＝BC＝3，点E，F分别在线段AB，AC上，且EF∥BC，将△AEF沿EF折起到△PEF的位置，使得二面角P－EF－B的大小为60°.(1)求证：EF⊥PB；(2)当点E为线段AB靠近B点的三等分点时，求四棱锥P－EBCF的侧面积．[解析](1)证明：由题意知BC⊥AB．∵EF∥BC，∴EF⊥AB，翻折后垂直关系没变，仍有EF⊥PE，EF⊥BE.又PE∩BE＝E，∴EF⊥平面PBE.又PB⊂平面PBE，∴EF⊥PB．(2)∵EF⊥AE，EF⊥BE，∴∠PEB是二面角P－EF－B的平面角，∴∠PEB＝60°.在△PBE中，PE＝2，BE＝1，由余弦定理得PB＝PE2＋BE2－2PE·BE cos60°＝3，∴PB2＋EB2＝PE2，∴PB⊥EB，∴PB，BC，EB两两垂直．又EF⊥PE，EF⊥BE，∴△PBE，△PBC，△PEF均为直角三角形．由△AEF∽△ABC可得，EF＝23BC＝2，S△PBC ＝12BC·PB＝332，S△PBE＝12PB·BE＝32，S△PEF＝12EF·PE＝2.如图，在四边形BCFE 中，过点F 作BC 的垂线，垂足为H ， 则FC 2＝FH 2＋HC 2＝BE 2＋(BC －EF )2＝2，所以FC ＝ 2.在△PFC 中，FC ＝2，PC ＝BC 2＋PB 2＝23， PF ＝PE 2＋EF 2＝2 2.由余弦定理可得，cos ∠PFC ＝PF 2＋FC 2－PC 22PF ·FC ＝－14，则sin ∠PFC ＝154， S △PFC ＝12PF ·FC ·sin ∠PFC ＝152. 所以四棱锥P －EBCF 的侧面积为S △PBC ＋S △PBE ＋S △PEF ＋S △PFC ＝2＋23＋152.。

直线、平面垂直的判定与性质[知识能否忆起]一、直线与平面垂直1．直线和平面垂直的定义直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直．2．直线与平面垂直的判定定理及推论文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫a，b⊂αa∩b＝Ol⊥al⊥b⇒l⊥α推论如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直这个平面⎭⎪⎬⎪⎫a∥ba⊥α⇒b⊥α3．直线与平面垂直的性质定理文字语言图形语言符号语言性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b二、平面与平面垂直1．平面与平面垂直的判定定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β2．平面与平面垂直的性质定理文字语言图形语言符号语言性质定理两个平面垂直，则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β＝al⊥a⇒l⊥α[小题能否全取]1．(教材习题改编)已知平面α，β，直线l，若α⊥β，α∩β＝l，则()A．垂直于平面β的平面一定平行于平面αB．垂直于直线l的直线一定垂直于平面αC．垂直于平面β的平面一定平行于直线lD．垂直于直线l的平面一定与平面α、β都垂直2.(2012·厦门模拟)如图，O为正方体ABCD－A1B1C1D1的底面ABCD的中心，则下列直线中与B1O 垂直的是()A．A1D B．AA1C．A1D1D．A1C13．已知α，β是两个不同的平面，m，n是两条不重合的直线，则下列命题中正确的是() A．若m∥α，α∩β＝n，则m∥nB．若m⊥α，m⊥n，则n∥αC．若m⊥α，n⊥β，α⊥β，则m⊥nD．若α⊥β，α∩β＝n，m⊥n，则m⊥β．4.如图，已知P A⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．5．(教材习题改编)如图，已知六棱锥P －ABCDEF的底面是正六边形，P A⊥平面ABC，P A ＝2AB.则下列命题正确的有________．①P A⊥AD；②平面ABC⊥平面PBC；③直线BC∥平面P AE；④直线PD与平面ABC所成角为30°.1.在证明线面垂直、面面垂直时，一定要注意判定定理成立的条件．同时抓住线线、线面、面面垂直的转化关系，即：2．在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决，如有平面垂直时，一般要用性质定理．3．几个常用的结论：(1)过空间任一点有且只有一条直线与已知平面垂直．(2)过空间任一点有且只有一个平面与已知直线垂直．垂直关系的基本问题典题导入[例1](2012·襄州模拟)若m，n为两条不重合的直线，α，β为两个不重合的平面，给出下列命题：①若m，n都平行于平面α，则m，n一定不是相交直线；②若m 、n 都垂直于平面α，则m ，n 一定是平行直线；③已知α，β互相垂直，m ，n 互相垂直，若m ⊥α，则n ⊥β；④m ，n 在平面α内的射影互相垂直，则m ，n 互相垂直．其中的假命题的序号是________．由题悟法解决此类问题常用的方法有：①依据定理条件才能得出结论的，可结合符合题意的图形作出判断；②否定命题时只需举一个反例．③寻找恰当的特殊模型(如构造长方体)进行筛选．直线与平面垂直的判定与性质典题导入[例2](2012·广东高考)如图所示，在四棱锥P －ABCD 中，AB ⊥平面P AD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点且DF ＝12AB ，PH 为△P AD 中AD 边上的高．(1)证明：PH ⊥平面ABCD ； (3)证明：EF ⊥平面P AB .由题悟法证明直线和平面垂直的常用方法有： (1)利用判定定理．(2)利用判定定理的推论(a ∥b ，a ⊥α⇒b ⊥α)． (3)利用面面平行的性质(a ⊥α，α∥β⇒a ⊥β)． (4)利用面面垂直的性质．当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面．以题试法2．(2012·启东模拟)如图所示，已知P A ⊥矩形ABCD 所在平面，M ，N 分别是AB ，PC 的中点． (1)求证：MN ⊥CD ；(2)若∠PDA ＝45°，求证：MN ⊥平面PCD .面面垂直的判定与性质典题导入[例3](2012·江苏高考)如图，在直三棱柱ABC －A 1B1C1中，A1B1＝A1C1，D，E分别是棱BC，CC1上的点(点D不同于点C)，且AD⊥DE ，F为B1C1的中点．求证：(1)平面ADE⊥平面BCC1B1；(2)直线A1F∥平面ADE..由题悟法1．判定面面垂直的方法：(1)面面垂直的定义．(2)面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．2．在已知平面垂直时，一般要用性质定理进行转化，转化为线面垂直或线线垂直．转化方法：在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．以题试法3．(2012·泸州一模)如图，在四棱锥P－ABCD 中，底面ABCD为菱形，∠BAD＝60°，Q为AD 的中点．(1)若P A＝PD，求证：平面PQB⊥平面P AD；(2)若点M在线段PC上，且PM＝tPC(t>0)，试确定实数t的值，使得P A∥平面MQB.1．(2012·杭州模拟)设a，b，c是三条不同的直线，α，β是两个不同的平面，则a⊥b的一个充分条件是()A．a⊥c，b⊥c B．α⊥β，a⊂α，b⊂βC．a⊥α，b∥αD．a⊥α，b⊥α.2．设α，β，γ是三个不重合的平面，l是直线，给出下列命题①若α⊥β，β⊥γ，则α⊥γ；②若l上两点到α的距离相等，则l∥α；③若l⊥α，l∥β，则α⊥β；④若α∥β，l⊄β，且l∥α，则l∥β.其中正确的命题是()A．①②B．②③C．②④D．③④3．给出命题：(1)在空间里，垂直于同一平面的两个平面平行；(2)设l，m是不同的直线，α是一个平面，若l ⊥α，l∥m，则m⊥α；(3)已知α，β表示两个不同平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；(4)a，b是两条异面直线，P为空间一点，过P 总可以作一个平面与a，b之一垂直，与另一个平行．其中正确命题个数是()A．0 B．1C．2 D．34.(2013·济南模拟)如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部．5.(2012·曲阜师大附中质检)如图所示，直线P A 垂直于⊙O所在的平面，△ABC内接于⊙O，且AB 为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面P AC 的距离等于线段BC的长．其中正确的是()A．①②B．①②③C．①D．②③6.(2012·济南名校模拟)如图，在四边形ABCD 中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下面命题正确的是()A．平面ABD⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ADC⊥平面ABC 7.如图所示，在四棱锥P－ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)8．(2012·忻州一中月考)正四棱锥S－ABCD的底面边长为2，高为2，E是BC的中点，动点P在四棱锥的表面上运动，并且总保持PE⊥AC，则动点P的轨迹的长为________．10. 如图所示，已知三棱锥A－BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．(1)求证：DM∥平面APC；(2)求证：平面ABC⊥平面APC.11.(2012·北京海淀二模)如图所示，P A⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，P A＝AB＝2，点E为线段PB的中点，点M在AB上，且OM∥AC.(1)求证：平面MOE∥平面P AC；(2)求证：平面P AC⊥平面PCB.。

[知能演练]一、选择题1．给定空间中的直线l及平面α.条件“直线l与平面α内无数条直线都垂直”是“直线l与平面α垂直”的() A．充要条件B．充分非必要条件C．必要非充分条件D．既非充分又非必要条件解析：若直线l与平面α垂直，由线面垂直的定义知，直线l垂直于平面α内的任意直线，所以直线l与平面α内无数条直线都垂直；但当直线l与平面α内无数条直线都垂直时，却不能得出直线l与平面α垂直，所以“直线l与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的必要非充分条件．答案：C2．设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是() A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β解析：选项A中，若a⊥α，b∥β，α⊥β，则有a⊥b或a∥b(b⊥α时)，故A错误；选项B中，若a⊥α，α∥β，则有a⊥β，又b⊥β，所以a∥b，因此B错误；选项C中，因为a⊂α，α∥β，所以a∥β，又因为b⊥β，所以a⊥b.反之，若a⊥b，则不一定有a⊂α，b⊥β，α∥β，所以C正确；选项D中，当b∥β，且b与α，β的交线平行或b⊂α时，a与b有垂直关系也有不垂直关系，当b∥β且b与α，β的交线垂直时，有a⊥b，所以D也不对．答案：C3．设α，β，γ是三个不重合的平面，l是直线，给出下列四个命题：①若α⊥β，l⊥β，则l∥α；②若l⊥α，l∥β，则α⊥β；③若l上有两点到α的距离相等，则l∥α；④若α⊥β，α∥γ，则γ⊥β.其中正确命题的序号是() A．①②B．①④C．②④D．③④解析：①若α⊥β，l⊥β，则l∥α或l⊂α，故①不正确；②l∥β，则过l作一平面γ使平面β与γ相交，交线设为l′，那么l∥l′，∵l⊥α，∴l′⊥α，又l′⊂β，∴α⊥β.故②正确；③不正确．如l与平面α相交；④正确．答案：C4．若两个平面α，β相交但不垂直，直线m在平面α内，则在平面β内()A．一定存在与直线m平行的直线B．一定不存在与直线m平行的直线C．一定存在与直线m垂直的直线D．一定不存在与直线m垂直的直线答案：C二、填空题5．如下图所示，在四棱锥P－ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)解析：由定理可知，BD⊥PC.∴当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD，而PC⊂平面PCD，∴平面MBD⊥平面PCD.答案：DM⊥PC(或BM⊥PC等)6．如图，正方体ABCD—A1B1C1D1的棱长是1，过A点作平面A1BD的垂线，垂足为点H，有下列三个命题：①点H是△A1BD的中心；②AH垂直于平面CB1D1；③AC1与B1C所成的角是90°.其中正确命题的序号是________．解析：由于ABCD－A1B1C1D1是正方体，所以A－A1BD是一个正三棱锥，因此A点在平面A1BD上的射影H是三角形A1BD的中心，故①正确；又因为平面CB1D1与平面A1BD 平行，所以AH⊥平面CB1D1，故②正确；从而可得AC1⊥平面CB1D1，即AC1与B1C垂直，所成的角等于90°.答案：①②③三、解答题7．如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E、F分别是AB、BD的中点，求证：(1)直线EF∥平面ACD；(2)平面EFC⊥平面BCD.证明：(1)在△ABD中，因为E、F分别是AB、BD的中点，所以EF∥AD.又AD⊂平面ACD，EF⊄平面ACD，所以直线EF∥平面ACD.(2)在△ABD中，因为AD⊥BD，EF∥AD，所以EF⊥BD.在△BCD中，因为CD＝CB，F为BD的中点，所以CF⊥BD.因为EF⊂平面EFC，CF⊂平面EFC，EF与CF交于点F，所以BD⊥平面EFC.又因为BD⊂平面BCD，所以平面EFC⊥平面BCD.8．如图所示，在三棱锥S－ABC中，SA⊥平面ABC，AB⊥BC，DE垂直平分SC，分别交AC、SC于D、E，且SA＝AB＝a，BC＝2a.(1)求证：SC⊥平面BDE；(2)求平面BDE与平面BDC所成二面角的大小．解：(1)∵SA⊥平面ABC，又AB、AC、BD⊂平面ABC，∴SA⊥AB，SA⊥AC，SA⊥BD.∴SB＝SA2＋AB2＝2a.∵BC＝2a，∴SB＝BC.∵E为SC的中点，∴BE⊥SC.又DE⊥SC，BE∩DE＝E，∴SC⊥平面BDE.(2)由(1)的结论及BD⊂平面BDE得BD⊥SC，又由(1)知BD⊥SA，∴BD⊥平面SAC.∴BD⊥DE，BD⊥DC.∴∠CDE为平面BDE与平面BDC所成二面角的平面角．∵AB⊥BC，∴AC＝AB2＋BC2＝a2＋2a2＝3a.在Rt△SAC中，tan∠SCA＝SAAC＝a3a＝33，∴∠SCA＝30°，∴∠CDE＝90°－∠SCA＝60°.[高考·模拟·预测]1．(2009·山东高考)已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的() A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：当α⊥β时，平面α内的直线m不一定和平面β垂直，但当平面α内的直线垂直于平面β时，根据面面垂直的判定定理，两个平面一定垂直，故“α⊥β”是“m⊥β”的必要不充分条件．答案：B2．(2009·浙江高考)在三棱柱ABC－A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是() A．30°B．45°C．60°D．90°解析：过A作AE⊥BC于点E，则易知AE⊥面BB1C1C，则∠ADE即为所求，又tan∠ADE＝AEDE＝3，故∠ADE＝60°.故选C.答案：C3．(2009·江苏高考)设α和β为不重合的两个平面，给出下列命题：(1)若α内的两条相交直线分别平行于β内的两条直线，则α平行于β(2)若α外一条直线l与α内的一条直线平行，则l和α平行；(3)设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直．上面命题中，真命题的序号是________(写出所有真命题的序号)．解析：(1)α内两条相交直线分别平行于平面β，则两条相交直线确定的平面α平行于平面β，正确．(2)平面α外一条直线l与α内的一条直线平行，则l平行于α，正确．(3)如图，α∩β＝l，a⊂α，a⊥l，但不一定有α⊥β，错误．(4)直线l与α垂直的充分必要条件是l与α内的两条相交直线垂直，而该命题缺少“相交”两字，故为假命题．综上所述，真命题的序号为(1)(2)．答案：(1)(2)4．(2009·山东高考)如图，在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA1＝2，E，E1分别是棱AD，AA1的中点．(Ⅰ)设F是棱AB的中点，证明：直线EE1∥平面FCC1，(Ⅱ)证明：平面D1AC⊥平面BB1C1C.(Ⅰ)证法一：取A1B1的中点为F1，连接FF1，C1F1.由于FF1∥BB1∥CC1，所以F1∈平面FCC1，因此平面FCC1即为平面C1CFF1.连接A1D，F1C.由于A1F1綊D1C1綊CD，所以四边形A1DCF1为平行四边形，因此A1D∥F1C.又EE1∥A1D，所以EE1∥F1C.而EE1⊄平面FCC1，F1C⊂平面FCC1，故EE1∥平面FCC1.证法二：因为F为AB的中点，CD＝2，AB＝4，AB∥CD.所以CD綊AF，因此四边形AFCD为平行四边形，所以AD∥FC.又CC1∥DD1，FC∩CC1＝C，FC⊂平面FCC1，CC1⊂平面FCC1，所以平面ADD1A1∥平面FCC1，又EE1⊂平面ADD1A1，所以EE1∥平面FCC1.(Ⅱ)证明：连接AC.在△FBC中，FC＝BC＝FB，又F为AB的中点，所以AF＝FC＝FB，因此∠ACB＝90°，即AC⊥BC.又AC⊥CC1，且CC1∩BC＝C，所以AC⊥平面BB1C1C，而AC⊂平面D1AC，故平面D1AC⊥平面BB1C1C.[备选精题]5．(2009·浙江高考)如右图，平面P AC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O分别为P A，PB，AC的中点，AC＝16，P A＝PC＝10.(1)设G是OC的中点，证明FG∥平面BOE；(2)证明在△ABO内存在一点M，使FM⊥平面BOE，并求点M到OA，OB的距离．(1)证明：如右图，取PE的中点为H，连结HG，HF.因为点E ，O ，G ，H 分别是P A ，AC ，OC ，PE 的中点， 所以HG ∥OE ，HF ∥EB . 因此平面FGH ∥平面BOE . 因为FG 在平面FGH 内， 所以FG ∥平面BOE .(2)解：在平面OAP 内，过点P 作PN ⊥OE ，交OA 于点N ，交OE 于点Q .连结BN ，过点F 作FM ∥PN ，交BN 于点M .下证FM ⊥平面BOE . 由题意，得OB ⊥平面P AC ， 所以OB ⊥PN .又因为PN ⊥OE ，所以PN ⊥平面BOE . 因此FM ⊥平面BOE .在Rt △OAP 中，OE ＝12P A ＝5，PQ ＝245，cos ∠NPO ＝PQ OP ＝45，ON ＝OP · tan ∠NPO ＝92<OA ，所以点N 在线段OA 上．因为F 是PB 的中点，所以M 是BN 的中点．因此点M 在△AOB 内，点M 到OA ，OB 的距离分别为12OB ＝4，12ON ＝94.。

[考纲传真] １．以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理.２．能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题．１．直线与平面垂直（１）定义：如果直线l与平面α内的任意一条直线都垂直，则直线l 与平面α垂直．（２）判定定理与性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直错误!⇒l⊥α性质定理垂直于同一个平面的两条直线平行错误!⇒a∥b（１）平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角．（２）当直线与平面垂直和平行（或直线在平面内）时，规定直线和平面所成的角分别为90°和0°.（３）范围：错误!.３．二面角的有关概念（１）二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．（２）二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角．（３）范围：[0，π]．４．平面与平面垂直（１）定义：如果两个平面所成的二面角是直二面角，就说这两个平面互相垂直．（２）判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直错误!⇒α⊥β性质定理两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直错误!⇒l⊥α１．直线与平面垂直的五个结论（１）若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线.（２）若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．（３）垂直于同一条直线的两个平面平行．（４）一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．（５）两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．２．三种垂直关系的转化线线垂直错误!线面垂直错误!面面垂直[基础自测]１．（思考辨析）判断下列结论的正误．（正确的打“√”，错误的打“×”）（１）直线l与平面α内的无数条直线都垂直，则l⊥α.（）（２）垂直于同一个平面的两平面平行．（）（３）直线a⊥α，b⊥α，则a∥b.（）（４）若α⊥β，a⊥β⇒a∥α.（）[答案] （１）×（２）×（３）√（４）×２．设l，m，n均为直线，其中m，n在平面α内，则“l⊥α”是“l⊥m且l⊥n”的（）Ａ．充分不必要条件Ｂ．必要不充分条件Ｃ．充要条件Ｄ．既不充分也不必要条件A [l⊥α⇒l⊥m，l⊥n；反之，不一定成立，因为m，n不一定相交，故选Ａ．]３．（教材改编）下列命题中不正确的是（）Ａ．如果平面α⊥平面β，且直线l∥平面α，则直线l⊥平面βＢ．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βＣ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βＤ．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥γA [A错误，l与β可能平行或相交，其余选项均正确．]４．（教材改编）如图所示，已知PA⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．４[∵PA⊥平面ABC，∴PA⊥AB，PA⊥AC，PA⊥BC，则△PAB，△PAC为直角三角形．由BC⊥AC，且AC∩PA＝A，∴BC⊥平面PAC，从而BC⊥PC.因此△ABC，△PBC也是直角三角形．]５．（教材改编）在三棱锥P­ABC中，点P在平面ABC中的射影为点O.（１）若PA＝PB＝PC，则点O是△ABC的________心；（２）若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的________心．（１）外（２）垂[（１）如图，∵PO⊥平面ABC，连接OA，OB，OC，在Rt△POA 中，OA２＝PA２—PO２，同理OB２＝PB２—PO２，OC２＝PC２—PO２.又PA＝PB＝PC，故OA＝OB＝OC，∴O是△ABC的外心．（２）由PA⊥PB，PA⊥PC可知PA⊥平面PBC，∴PA⊥BC，又PO⊥BC，∴BC⊥平面PAO，∴AO⊥BC，同理BO⊥AC，CO⊥AB.故O是△ABC的垂心．]直线与平面垂直的判定与性质【例１】如图所示，在四棱锥P­ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：（１）CD⊥AE；（２）PD⊥平面ABE.[证明] （１）在四棱锥P­ABCD中，∵PA⊥底面ABCD，CD⊂平面ABCD，∴PA⊥CD.又∵AC⊥CD，PA∩AC＝A，PA，AC⊂平面PAC，∴CD⊥平面PAC.而AE⊂平面PAC，∴CD⊥AE.（２）由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC.由（１）知AE⊥CD，且PC∩CD＝C，PC，CD⊂平面PCD，∴AE⊥平面PCD，而PD⊂平面PCD，∴AE⊥PD.∵PA⊥底面ABCD，AB⊂平面ABCD，∴PA⊥AB.又∵AB⊥AD，且PA∩AD＝A，∴AB⊥平面PAD，而PD⊂平面PAD，∴AB⊥PD.又∵AB∩AE＝A，AB，AE⊂平面ABE，∴PD⊥平面ABE.[规律方法] 证明直线和平面垂直的常用方法１利用判定定理.２利用判定定理的推论a∥b，a⊥α⇒b⊥α.３利用面面平行的性质a⊥α，α∥β⇒a⊥β.４利用面面垂直的性质.,当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.５重视平面几何知识，特别是勾股定理的应用.如图所示，已知AB为圆O的直径，点D为线段AB上一点，且AD＝错误!DB，点C为圆O上一点，且BC＝错误!AC，PD⊥平面ABC，PD＝DB.求证：PA⊥CD.[证明] 因为AB为圆O的直径，所以AC⊥CB，在Rt△ACB中，由错误!AC＝BC，得∠ABC＝３0°.设AD＝１，由３AD＝DB，得DB＝３，BC＝２错误!，由余弦定理得CD２＝DB２＋BC２—２DB·BC cos ３0°＝３，所以CD２＋DB２＝BC２，即CD⊥AB.因为PD⊥平面ABC，CD⊂平面ABC，所以PD⊥CD，由PD∩AB＝D，得CD⊥平面PAB，又PA⊂平面PAB，所以PA⊥CD.平面与平面垂直的判定与性质【例２】（２0１8·北京高考节选）如图，在四棱锥P­ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，E是AD的中点．求证：（１）PE⊥BC；（２）平面PAB⊥平面PCD.[证明] （１）∵PA＝PD，E是AD的中点，∴PE⊥AD.又ABCD为矩形，∴AD∥BC，∴PE⊥BC.（２）因为ABCD为矩形，所以AB⊥AD.又平面PAD⊥平面ABCD，所以AB⊥平面PAD，所以AB⊥PD.又PA⊥PD，所以PD⊥平面PAB.又PD⊂平面PCD，所以平面PAB⊥平面PCD.[规律方法] １．判定面面垂直的方法１面面垂直的定义；２面面垂直的判定定理a⊥β，a⊂α⇒α⊥β.２．在已知平面垂直时，一般要用性质定理进行转化.在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直.点，BE⊥平面ABCD.（１）证明：平面AEC⊥平面BED；（２）若∠ABC＝１２0°，AE⊥EC，三棱锥E­ACD的体积为错误!，求该三棱锥的侧面积．[解] （１）证明：因为四边形ABCD为菱形，所以AC⊥BD.因为BE⊥平面ABCD，所以AC⊥BE.故AC⊥平面BED.又AC⊂平面AEC，所以平面AEC⊥平面BED.（２）设AB＝x，在菱形ABCD中，由∠ABC＝１２0°，可得AG＝GC＝错误!x，GB＝GD＝错误!.因为AE⊥EC，所以在Rt△AEC中，可得EG＝错误!x.由BE⊥平面ABCD，知△EBG为直角三角形，可得BE＝错误!x.由已知得，三棱锥E­ACD的体积V E­ACD＝错误!×错误!AC·GD·BE＝错误!x３＝错误!，故x＝２．从而可得AE＝EC＝ED＝错误!.所以△EAC的面积为３，△EAD的面积与△ECD的面积均为错误!.故三棱锥E­ACD的侧面积为３＋２错误!.平行与垂直的综合问题【例３】如图１，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝２CD，DE⊥AB，沿DE将△AED 折起到△A１ED的位置，连接A１B，A１C，M，N分别为A１C，BE的中点，如图２．图１图２（１）求证：DE⊥A１B；（２）求证：MN∥平面A１ED；（３）在棱A１B上是否存在一点G，使得EG⊥平面A１BC？若存在，求出错误!的值；若不存在，说明理由．[解] （１）证明：∵在直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝２CD，DE⊥AB，沿DE将△AED折起到△A１ED的位置，∴DE⊥A１E，DE⊥BE，∵A１E∩BE＝E，∴DE⊥平面A１BE，∵A１B⊂平面A１BE，∴DE⊥A１B.（２）证明：取CD中点F，连接NF，MF，∵M，N分别为A１C，BE的中点，∴MF∥A１D，NF∥DE，又DE∩A１D＝D，NF∩MF＝F，DE⊂平面A１DE，A１D⊂平面A１DE，NF⊂平面MNF，MF⊂平面MNF.∴平面A１DE∥平面MNF，∴MN∥平面A１ED.（３）取A１B的中点G，连接EG，∵A１E＝BE，∴EG⊥A１B，由（１）知DE⊥平面A１BE，∵DE∥BC，∴BC⊥平面A１BE，∴EG⊥BC，又A１B∩BC＝B，∴EG⊥平面A１BC.故棱A１B上存在中点G，使得EG⊥平面A１BC，此时错误!＝１．[规律方法] 证明折叠问题中的平行与垂直，关键是分清折叠前后图形的位置和数量关系的变与不变.一般地，折叠前位于“折痕”同侧的点、线间的位置和数量关系折叠后不变，而折叠前位于“折痕”两侧的点、线间的位置关系折叠后会发生变化.对于不变的关系可在平面图形中处理，而对于变化的关系则要在立体图形中解决.延长AE交BC于点F，将△ABD沿BD折起，得到三棱锥A１­BCD，如图２所示．图１图２（１）若M是FC的中点，求证：直线DM∥平面A１EF；（２）求证：BD⊥A１F；（３）若平面A１BD⊥平面BCD，试判断直线A１B与直线CD能否垂直？请说明理由．[解] （１）证明：因为D，M分别为AC，FC的中点，所以DM∥EF.又EF⊂平面A１EF，DM⊄平面A１EF，所以DM∥平面A１EF.（２）证明：因为A１E⊥BD，EF⊥BD，且A１E∩EF＝E，所以BD⊥平面A１EF.又A１F⊂平面A１EF，故BD⊥A１F.（３）A１B与CD不能垂直．因为平面A１BD⊥平面BCD，平面A１BD∩平面BCD＝BD，EF⊥BD，EF⊂平面BCD，∴EF⊥平面A１BD.∴EF⊥A１B，又EF∥DM，∴A１B⊥DM.若A１B⊥CD，则A１B⊥平面BCD.所以A１B⊥BD，这与∠A１BD为锐角矛盾．所以A１B与CD不能垂直．１如果m⊥n，m⊥α，n∥β，那么α⊥β.２如果m⊥α，n∥α，那么m⊥n.３如果α∥β，m⊂α，那么m∥β.４如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________．（填写所有正确命题的编号）２３４[根据相关知识，对四个命题逐个判断．对于１，α，β可以平行，可以相交也可以垂直，故错误．对于２，由线面平行的性质定理知存在直线l⊂α，n∥l，又m⊥α，所以m⊥l，所以m⊥n，故正确．对于３，因为α∥β，所以α，β没有公共点．又m⊂α，所以m，β没有公共点，由线面平行的定义可知m∥β，故正确．对于４，因为m∥n，所以m与α所成的角和n与α所成的角相等．因为α∥β，所以n与α所成的角和n与β所成的角相等，所以m与α所成的角和n与β所成的角相等，故正确．]２．（２0１8·全国卷Ⅲ）如图，边长为２的正方形ABCD所在的平面与半圆弧错误!所在平面垂直，M是错误!上异于C，D的点．（１）证明：平面AMD⊥平面BMC；（２）当三棱锥M­ABC体积最大时，求面MAB与面MCD所成二面角的正弦值．[解] （１）证明：由题设知，平面CMD⊥平面ABCD，交线为CD.因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，所以BC⊥DM.因为M为错误!上异于C，D的点，且DC为直径，所以DM⊥CM.又BC∩CM＝C，所以DM⊥平面BMC.而DM⊂平面AMD，故平面AMD⊥平面BMC.（２）以D为坐标原点，错误!的方向为x轴正方向，建立如图所示的空间直角坐标系D­xyz.当三棱锥M­ABC体积最大时，M为错误!的中点．由题设得D（0,0,0），A（２,0,0），B（２,２,0），C（0,２,0），M（0,１,１），错误!＝（—２,１,１），错误!＝（0,２,0），错误!＝（２,0,0）．设n＝（x，y，z）是平面MAB的法向量，则错误!即错误!可取n＝（１,0,２）．错误!是平面MCD的法向量，因此cos〈n，错误!〉＝错误!＝错误!，sin〈n，错误!〉＝错误!.所以面MAB与面MCD所成二面角的正弦值是错误!.。

第5讲直线、平面垂直的判定与性质一、知识梳理1．直线与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫a，b⊂αa∩b＝Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b2.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β性质定理两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直⎭⎪⎬⎪⎫α⊥βl⊂βα∩β＝al⊥a⇒l⊥α3.直线与平面所成的角(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角，如图，∠PAO就是斜线AP与平面α所成的角．(2)线面角θ的X 围：θ∈⎣⎢⎡⎦⎥⎤0，π2.①直线垂直于平面，则它们所成的角是直角；②直线和平面平行或在平面内，则它们所成的角是0°的角； ③当直线与平面斜交时，它们所成的角是锐角． 常用结论1．与线面垂直相关的两个常用结论：(1)两平行线中的一条与平面垂直，则另一条也与这个平面垂直． (2)一条直线垂直于两平行平面中的一个，则与另一个平面也垂直． 2．三种垂直关系的转化：线线垂直判定定理性质定理线面垂直判定定理性质定理面面垂直二、习题改编1．(必修2P72探究改编)已知互相垂直的平面α，β交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则( )A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n解析：选C.由题意知，α∩β＝l ，所以l ⊂β，因为n ⊥β，所以n ⊥l . 2．(必修2P67练习T2改编)在三棱锥P ­ABC 中，点P 在平面ABC 中的射影为点O . (1)若PA ＝PB ＝PC ，则点O 是△ABC 的心；(2)若PA ⊥PB ，PB ⊥PC ，PC ⊥PA ，则点O 是△ABC 的心．解析：(1)如图，连接OA ，OB ，OC ，OP ，在Rt △POA ，Rt △POB 和Rt △POC 中，PA ＝PB ＝PC ，所以OA ＝OB ＝OC ，即O 为△ABC 的外心．(2)如图，延长AO ，BO ，CO 分别交BC ，AC ，AB 于点H ，D ，G .因为PC ⊥PA ，PB ⊥PC ，PA ∩PB ＝P ，所以PC⊥平面PAB，又AB⊂平面PAB，所以PC⊥AB，因为AB⊥PO，PO∩PC＝P，所以AB⊥平面PGC，又CG⊂平面PGC，所以AB⊥CG，即CG为△ABC边AB上的高．同理可证BD，AH分别为△ABC边AC，BC上的高，即O为△ABC的垂心．答案：(1)外(2)垂一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)已知直线a，b，c，若a⊥b，b⊥c，则a∥c.( )(2)直线l与平面α内的无数条直线都垂直，则l⊥α.( )(3)设m，n是两条不同的直线，α是一个平面，若m∥n，m⊥α，则n⊥α.( )(4)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．( )(5)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.( )答案：(1)×(2)×(3)√(4)×(5)×二、易错纠偏常见误区(1)证明线面垂直时，易忽视平面内两条直线为相交直线这一条件；(2)面面垂直的判定中找不到哪个面和哪条线垂直．1．(2020·某某江南十校联考)已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是( )A．α⊥β且m⊂αB．m⊥n且n∥βC．m∥n且n⊥βD．m⊥n且α∥β解析：选C.由线线平行性质的传递性和线面垂直的判定定理，可知C正确．2．(2020·某某某某第一次(3月)双基测试)已知直线l和平面α，β，且l⊂α，则“l⊥β”是“α⊥β”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选A.由面面垂直的判定定理可得，若l⊂α，l⊥β，则α⊥β，充分性成立；若l⊥β，α⊥β，则l⊂α或l∥α，必要性不成立，所以若l⊂α，则“l⊥β”是“α⊥β”的充分不必要条件，故选A.线面垂直的判定与性质(师生共研)(1)(2018·高考全国卷Ⅱ节选)如图，在三棱锥P ­ABC 中，AB ＝BC ＝22，PA ＝PB＝PC ＝AC ＝4，O 为AC 的中点．证明：PO ⊥平面ABC .(2)(2020·某某市七校联合考试)如图，直三棱柱ABC ­A 1B 1C 1的所有棱长都是2，D ，E 分别是AC ，CC 1的中点．求证：AE ⊥平面A 1BD .【证明】 (1)因为AP ＝CP ＝AC ＝4，O 为AC 的中点， 所以OP ⊥AC ，且OP ＝2 3. 连接OB .因为AB ＝BC ＝22AC ， 所以△ABC 为等腰直角三角形， 且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知，PO ⊥OB . 由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC .(2)因为AB ＝BC ＝CA ，D 是AC 的中点，所以BD ⊥AC ，因为直三棱柱ABC ­A 1B 1C 1中，AA 1⊥平面ABC ，所以平面AA 1C 1C ⊥平面ABC ， 所以BD ⊥平面AA 1C 1C ，所以BD ⊥AE .又在正方形AA 1C 1C 中，D ，E 分别是AC ，CC 1的中点， 所以A 1D ⊥AE .又A 1D ∩BD ＝D ， 所以AE ⊥平面A 1BD .判定线面垂直的四种方法如图，在直三棱柱ABC­A1B1C1中，底面ABC是正三角形，M，N分别是AB，AA1的中点，且A1M⊥B1N.求证：B1N⊥A1C.证明：连接CM，在直三棱柱ABC­A1B1C1中，AA1⊥平面ABC，CM⊂平面ABC，所以AA1⊥CM.在△ABC中，AC＝BC，AM＝BM，所以CM⊥AB.又AA1∩AB＝A，所以CM⊥平面ABB1A1.因为B1N⊂平面ABB1A1，所以CM⊥B1N.又A1M⊥B1N，A1M∩CM＝M，所以B1N⊥平面A1CM.因为A1C⊂平面A1CM，所以B1N⊥A1C.面面垂直的判定与性质(师生共研)(2019·高考卷节选)如图，在四棱锥P­ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD⊥平面PAC；(2)若∠ABC＝60°，求证：平面PAB⊥平面PAE.【证明】(1)因为PA⊥平面ABCD，所以PA⊥BD.因为底面ABCD为菱形，所以BD⊥AC.又PA∩AC＝A，所以BD⊥平面PAC.(2)因为PA⊥平面ABCD，AE⊂平面ABCD，所以PA⊥AE.因为底面ABCD为菱形，∠ABC＝60°，且E为CD的中点，所以AE⊥CD.所以AB⊥AE.又AB∩PA＝A，所以AE⊥平面PAB.因为AE⊂平面PAE，所以平面PAB⊥平面PAE.(1)证明面面垂直的方法①定义法：利用面面垂直的定义，即判定两平面所成的二面角为直二面角，将证明面面垂直的问题转化为证明平面角为直角的问题．②定理法：利用面面垂直的判定定理，即证明其中一个平面经过另一个平面的一条垂线，进而把问题转化为证明线线垂直加以解决．(2)在已知平面垂直时，一般要用性质定理进行转化．在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．如图，在三棱锥A­BCD中，△ABC是等边三角形，∠BAD＝∠BCD＝90°，点P是AC的中点，连接BP，DP.证明：平面ACD⊥平面BDP.证明：因为△ABC是等边三角形，∠BAD＝∠BCD＝90°，所以Rt△ABD≌Rt△CBD，可得AD＝CD.因为点P是AC的中点，所以PD⊥AC，PB⊥AC，因为PD∩PB＝P，PD⊂平面PBD，PB⊂平面PBD，所以AC⊥平面PBD.因为AC⊂平面ACD，所以平面ACD⊥平面BDP.直线与平面所成的角(师生共研)(2020·某某六盘山高级中学二模)空间四边形PABC中，PA⊥平面ABC，AC⊥BC，AC ＝BC ＝2，PA ＝4，则PC 和平面PAB 所成角的正切值为．【解析】 取AB 的中点O ， 连接CO ，PO ，易知CO ⊥平面PAB ，则∠CPO 为PC 和平面PAB 所成的角．易得CO ＝2，PO ＝32，所以tan ∠CPO ＝CO PO ＝13，所以PC 和平面PAB 所成角的正切值为13.【答案】 13求直线和平面所成角的步骤(1)寻找过斜线上一点与平面垂直的直线．(2)连接垂足和斜足得到斜线在平面上的射影，斜线与其射影所成的锐角或直角即为所求的角．(3)把该角归结在某个三角形中，通过解三角形，求出该角．1．(2018·高考全国卷Ⅰ)在长方体ABCD ­A 1B 1C 1D 1中，AB ＝BC ＝2，AC 1与平面BB 1C 1C 所成的角为30°，则该长方体的体积为( )A ．8B ．6 2C ．8 2D ．8 3解析：选C.连接BC 1，因为AB ⊥平面BB 1C 1C ，所以∠AC 1B ＝30°，AB ⊥BC 1，所以△ABC 1为直角三角形．又AB ＝2，所以BC 1＝2 3.又B 1C 1＝2，所以BB 1＝（23）2－22＝22，故该长方体的体积V ＝2×2×22＝8 2.2．已知边长为2的正方形ABCD 的四个顶点在球O 的球面上，球O 的体积V 球＝1605π3，则OA 与平面ABCD 所成的角的余弦值为．解析：如图，过点O 作OM ⊥平面ABCD ，垂足为点M ，则点M 为正方形ABCD 的中点．因为正方形ABCD 的边长为2，所以AC ＝22，所以AM ＝ 2.因为V 球＝43πr 3＝1605π3，所以球O 的半径OA ＝r ＝25，OA 与平面ABCD 所成的角的余弦值为cos ∠OAM ＝AM OA ＝225＝1010.答案：1010核心素养系列16 逻辑推理——空间中平行与垂直的证明如图，在四棱锥P ­ABCD 中，AB ∥CD ，AB ⊥AD ，CD ＝2AB ，平面PAD ⊥底面ABCD ，PA ⊥AD ，E 和F 分别是CD 和PC 的中点，求证：(1)PA ⊥底面ABCD ； (2)BE ∥平面PAD ； (3)平面BEF ⊥平面PCD .【证明】 (1)因为平面PAD ⊥底面ABCD ， 且PA 垂直于这两个平面的交线AD ，PA ⊂平面PAD ， 所以PA ⊥底面ABCD .(2)因为AB ∥CD ，CD ＝2AB ，E 为CD 的中点， 所以AB ∥DE ，且AB ＝DE ， 所以四边形ABED 为平行四边形． 所以BE ∥AD .又因为BE ⊄平面PAD ，AD ⊂平面PAD ， 所以BE ∥平面PAD .(3)因为AB ⊥AD ，而且ABED 为平行四边形． 所以BE ⊥CD ，AD ⊥CD ，由(1)知PA ⊥底面ABCD ，CD ⊂平面ABCD ，所以PA ⊥CD ，且PA ∩AD ＝A ，PA ，AD ⊂平面PAD ， 所以CD ⊥平面PAD ，又PD ⊂平面PAD ， 所以CD ⊥PD .因为E 和F 分别是CD 和PC 的中点， 所以PD ∥EF .所以CD ⊥EF ，又BE ⊥CD 且EF ∩BE ＝E ， 所以CD ⊥平面BEF ，又CD ⊂平面PCD ， 所以平面BEF ⊥平面PCD .本题考查数学核心素养中的逻辑推理及直观想象、逻辑推理让学生能发现问题和提出问题；能掌握推理的基本形式，表述论证的过程；能理解数学知识之间的联系，构建知识框架；形成有论据、有条理、合乎逻辑的思维品质，增强数学交流能力．(2020·某某市模拟试题(一))如图，在四棱锥P ­ABCD 中，底面ABCD是菱形，∠BAD ＝60°，PA ＝PD ＝AD ＝2，点M 在线段PC 上，且PM ＝2MC ，N 为AD 的中点．(1)求证：AD ⊥平面PNB ；(2)若平面PAD ⊥平面ABCD ，求三棱锥P ­NBM 的体积． 解：(1)证明：连接BD . 因为PA ＝PD ，N 为AD 的中点， 所以PN ⊥AD .又底面ABCD 是菱形，∠BAD ＝60°， 所以△ABD 为等边三角形， 所以BN ⊥AD .又PN ∩BN ＝N ， 所以AD ⊥平面PNB . (2)因为PA ＝PD ＝AD ＝2， 所以PN ＝NB ＝ 3.又平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，PN ⊥AD ， 所以PN ⊥平面ABCD .所以PN ⊥NB ，所以S △PNB ＝12×3×3＝32.因为AD ⊥平面PNB ，AD ∥BC ，所以BC ⊥平面PNB . 又PM ＝2MC ，所以V P ­NBM ＝V M ­PNB ＝23V C ­PNB ＝23×13×32×2＝23.[基础题组练]1．设α为平面，a ，b 为两条不同的直线，则下列叙述正确的是( ) A ．若a ∥α，b ∥α，则a ∥b B ．若a ⊥α，a ∥b ，则b ⊥α C ．若a ⊥α，a ⊥b ，则b ∥α D ．若a ∥α，a ⊥b ，则b ⊥α解析：选B.若a ∥α，b ∥α，则a 与b 相交、平行或异面，故A 错误；易知B 正确；若a ⊥α，a ⊥b ，则b ∥α或b ⊂α，故C 错误；若a ∥α，a ⊥b ，则b ∥α或b ⊂α，或b 与α相交，故D 错误．故选B.2．(2020·某某一模)设m ，n 是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是( )A ．若α⊥β，m ∥α，n ∥β，则m ⊥nB ．若m ⊥α，m ∥n ，n ∥β，则α⊥βC ．若m ⊥n ，m ⊂α，n ⊂β，则α⊥βD ．若α∥β，m ⊂α，n ⊂β，则m ∥n解析：选B.若α⊥β，m ∥α，n ∥β，则m 与n 相交、平行或异面，故A 错误； 因为m ⊥α，m ∥n ，所以n ⊥α， 又因为n ∥β，所以α⊥β，故B 正确；若m ⊥n ，m ⊂α，n ⊂β，则α与β的位置关系不确定，故C 错误； 若α∥β，m ⊂α，n ⊂β，则m ∥n 或m ，n 异面， 故D 错误．3.如图，在正四面体PABC 中，D ，E ，F 分别是AB ，BC ，CA 的中点，下面四个结论不成立的是( )A ．BC ∥平面PDFB ．DF ⊥平面PAEC．平面PDF⊥平面PAED．平面PDE⊥平面ABC解析：选D.因为BC∥DF，DF⊂平面PDF，BC⊄平面PDF，所以BC∥平面PDF，故选项A 正确．在正四面体中，AE⊥BC，PE⊥BC，DF∥BC，所以BC⊥平面PAE，则DF⊥平面PAE，从而平面PDF⊥平面PAE.因此选项B，C均正确．4．(2020·某某某某一模)在三棱锥P­ABC中，已知PA＝AB＝AC，∠BAC＝∠PAC，点D，E分别为棱BC，PC的中点，则下列结论正确的是( )A．直线DE⊥直线AD B．直线DE⊥直线PAC．直线DE⊥直线AB D．直线DE⊥直线AC解析：选D.如图，因为PA＝AB＝AC，∠BAC＝∠PAC，所以△PAC≌△BAC，所以PC＝BC，取PB的中点G，连接AG，CG，则PB⊥CG，PB⊥AG，又因为AG∩CG＝G，所以PB⊥平面CAG，则PB⊥AC，因为D，E分别为棱BC，PC的中点，所以DE∥PB，则DE⊥AC.故选D.5．(2019·高考卷)已知l，m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α.以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：．解析：其中两个论断作为条件，一个论断作为结论，可组成3个命题．命题(1)：若l⊥m，m∥α，则l⊥α，此命题不成立，可以举一个反例，例如在正方体ABCD­A1B1C1D1中，设平面ABCD为平面α，A1D1和A1B1分别为l和m，满足条件，但结论不成立．命题(2)：若l⊥m，l⊥α，则m∥α，此命题正确．证明：作直线m1∥m，且与l相交，故l与m1确定一个平面β，且l⊥m1，因为l⊥α，所以平面α与平面β相交，设α∩β＝n，则l⊥n，又m1，n⊂β，所以m1∥n，又m1∥m，所以m∥n，又m在平面α外，n⊂α，故m∥α.命题(3)：若m∥α，l⊥α，则l⊥m，此命题正确．证明：过直线m作一平面，且与平面α相交，交线为a，因为m∥α，所以m∥a.因为l⊥α，a⊂α，所以l⊥a，又m∥a，所以l⊥m.答案：②③⇒①或①③⇒②(答案不唯一)6．如图，已知∠BAC＝90°，PC⊥平面ABC，则在△ABC，△PAC的边所在的直线中，与PC垂直的直线有；与AP垂直的直线有．解析：因为PC⊥平面ABC，所以PC垂直于直线AB，BC，AC.因为AB⊥AC，AB⊥PC，AC∩PC＝C，所以AB⊥平面PAC，又因为AP⊂平面PAC，所以AB⊥AP，与AP垂直的直线是AB.答案：AB，BC，ACAB7.如图，在四棱锥P­ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面PAC；(2)求证：平面PAB⊥平面PAC.证明：(1)因为PC⊥平面ABCD，DC⊂平面ABCD，所以PC⊥DC.又因为AC⊥DC，且PC∩AC＝C，所以DC⊥平面PAC.(2)因为AB∥CD，DC⊥AC，所以AB⊥AC.因为PC⊥平面ABCD，AB⊂平面ABCD，所以PC⊥AB.又因为PC∩AC＝C，所以AB⊥平面PAC.又AB ⊂平面PAB ， 所以平面PAB ⊥平面PAC .8．(2020·某某部分学校调研)如图，已知直三棱柱ABC ­A 1B 1C 1中，AC ＝BC ＝AA 1＝1，AC ⊥BC ，E 在AB 上，且BA ＝3BE ，G 在AA 1上，且AA 1＝3GA 1.(1)求三棱锥A 1­ABC 1的体积； (2)求证：AC 1⊥EG .解：(1)在直三棱柱ABC ­A 1B 1C 1中，BC ⊥AC ，所以BC ⊥平面ACC 1A 1， 所以B 到平面ACC 1A 1的距离为1，所以VA 1­ABC 1＝VB ­AA 1C 1＝13×(12×1×1)×1＝16.(2)证明：如图，在AC 上取点D ，使CD ＝13CA ，连接ED ，DG ，因为BE ＝13BA ，所以DE ∥BC ，又BC ⊥平面ACC 1A 1， 所以DE ⊥平面ACC 1A 1. 又AC 1⊂平面ACC 1A 1， 所以DE ⊥AC 1. 在正方形ACC 1A 1中， 由CD ＝13CA ，A 1G ＝13A 1A ，得DG ⊥AC 1. 又DE ∩DG ＝D ， 所以AC 1⊥平面DEG . 所以AC 1⊥EG .[综合题组练]1.如图，棱长为1的正方体ABCD ­A 1B 1C 1D 1中，P 为线段A 1B 上的动点，则下列结论不正确的是( )A ．平面D 1A 1P ⊥平面A 1APB ．∠APD 1的取值X 围是⎝⎛⎭⎪⎫0，π2C ．三棱锥B 1­D 1PC 的体积为定值 D ．DC 1⊥D 1P解析：选B.在A 中，因为A 1D 1⊥平面A 1AP ，A 1D 1⊂平面D 1A 1P ，所以平面D 1A 1P ⊥平面A 1AP ，故A 正确；在B 中，当P 与A 1重合时，∠APD 1＝π2，故B 错误；在C 中，因为△B 1D 1C 的面积是定值，A 1B ∥平面B 1D 1C ，所以点P 到平面B 1D 1C 的距离是定值，所以三棱锥B 1­D 1PC 的体积为定值，故C 正确；在D 中，因为DC 1⊥D 1C ，DC 1⊥BC ，D 1C ∩BC ＝C ，D 1C ，BC ⊂平面BCD 1A 1，所以DC 1⊥平面BCD 1A 1，所以DC 1⊥D 1P ，故D 正确．2．(2018·高考全国卷Ⅱ)已知圆锥的顶点为S ，母线SA ，SB 互相垂直，SA 与圆锥底面所成角为30°.若△SAB 的面积为8，则该圆锥的体积为．解析：由题意画出图形，如图，设AC 是底面圆O 的直径，连接SO ，则SO 是圆锥的高．设圆锥的母线长为l ，则由SA ⊥SB ，△SAB 的面积为8，得12l 2＝8，得l Rt △ASO 中，由题意知∠SAO ＝30°，所以SO ＝12l ＝2，AO ＝32l ＝2 3.故该圆锥的体积V ＝13π×AO 2×SO ＝13π×(23)2×2＝8π.答案：8π3.如图，四棱锥P ­ABCD 的底面是正方形，PA ⊥底面ABCD ，PA ＝AD ＝2，点M ，N 分别在棱PD ，PC 上，且PC ⊥平面AMN .(1)求证：AM ⊥PD ；(2)求直线CD 与平面AMN 所成角的正弦值．解：(1)证明：因为四边形ABCD 是正方形，所以CD ⊥AD . 又因为PA ⊥底面ABCD ，所以PA ⊥CD ，故CD ⊥平面PAD . 又AM ⊂平面PAD ，则CD ⊥AM ，而PC ⊥平面AMN ，有PC ⊥AM ，又PC ∩CD ＝C ，则AM ⊥平面PCD ，故AM ⊥PD .(2)延长NM ，CD 交于点E ，因为PC ⊥平面AMN ，所以NE 为CE 在平面AMN 内的射影，故∠CEN 为CD (即CE )与平面AMN 所成的角， 又因为CD ⊥PD ，EN ⊥PN ，则有∠CEN ＝∠MPN ， 在Rt △PMN 中，sin ∠MPN ＝MN PM ＝33， 故CD 与平面AMN 所成角的正弦值为33. 4．(2020·某某七校联考)如图，在四棱锥P ­ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为正方形，PA ＝AB ＝2，E 是AB 的中点，G 是PD 的中点．(1)求四棱锥P ­ABCD 的体积； (2)求证：AG ∥平面PEC ； (3)求证：平面PCD ⊥平面PEC .解：(1)易知V 四棱锥P ­ABCD ＝13S 正方形ABCD ·PA ＝13×2×2×2＝83.(2)证明：如图，取PC 的中点F ，连接EF 和FG ，则易得AE ∥FG ，且AE ＝12CD ＝FG ，所以四边形AEFG 为平行四边形，所以EF ∥AG . 因为EF ⊂平面PEC ，AG ⊄平面PEC ， 所以AG ∥平面PEC .(3)证明：易知CD ⊥AD ，CD ⊥PA ，因为PA ∩AD ＝A ，PA ⊂平面PAD ，AD ⊂平面PAD ， 所以CD ⊥平面PAD .又AG ⊂平面PAD ，所以CD ⊥AG .易知PD ⊥AG ，因为PD ∩CD ＝D ，PD ⊂平面PCD ，CD ⊂平面PCD ， 所以AG ⊥平面PCD ， 所以EF ⊥平面PCD . 又EF ⊂平面PEC ， 所以平面PEC ⊥平面PCD .。