裂纹扩展的扩展有限元(xfem)模拟实例详解
- 格式:doc
- 大小:1.03 MB
- 文档页数:9

ABAQUS中扩展有限元(XFEM)功能简介扩展有限元(Extended Finite Element Method)是一种解决断裂力学问题的新的有限元方法,其理论最早于1999年,由美国西北大学的教授Belyschko和Black首次提出,主要是采用独立于网格剖分的思想解决有限元中的裂纹扩展问题,在保留传统有限元所有优点的同时,并不需要对结构内部存在的裂纹等缺陷进行网格划分。
ABAQUS基于在非线性方面的突出优势,在其6.9的版本中开始加入了扩展有限元功能,到6.13做了一些修正,加入了一些可以被CAE支持的关键字。
目前为止,除了手动编程,能够实现扩展有限元常用的商业软件只有ABAQUS,今天,我们就来谈谈ABAQUS 中如何实现扩展有限元。
1. XFEM理论在XFEM理论出现之前,所有对裂纹的静态模拟(断裂)都基本上是采用预留裂缝缺角,通过细化网格仿真裂缝的轮廓。
而动态的模拟(损伤)基本上都是基于统计原理的Paris 方法。
然而,断裂和损伤的结合问题却一直没有得到有效的解决,究其原因,在于断裂力学认可裂纹尖端的应力奇异现象(就是在靠近裂尖的区域应力值会变无穷大),并且尽可能的绕开这个区域。
而损伤力学又没有办法回避这个问题(裂纹都是从尖端开裂的)。
从理论上讲,其实单元内部的位移函数(形函数)可以是任意形状的,但大多数的计算软件都采用了多项式或者插值多项式作为手段来描述单元内部的位移场,这是因为采用这种方法更加便于在编程中进行处理。
但是这种方法的缺点就是,由于形函数的连续性,导致单元内部不可能存在间断。
直到Belytschko提出采用水平集函数作为手段,其基本形式为和上面左边的等式描述了单元内裂缝的位置,右边的等式描述了裂尖的位置。
与之对应的形函数便是和其中H(x)是阶跃函数。
想要了解更深的内容,大家可以参考《Extended Finite Element Method》和庄老师的《扩展有限单元法》这种扩充形函数能够描述单元内位移场在裂缝两边的跳跃性,同时,由于裂缝存在于单元内部,其扩展独立与其他单元,使得计算变得高效。

文章主题:基于xfem的垂直于双材料界面的裂纹扩展问题在材料科学和工程领域,裂纹扩展问题一直是一个备受关注的研究课题。
特别是在双材料界面上的裂纹扩展问题,由于双材料特性的不均匀性和复杂性,增加了研究和分析的难度。
在本文中,我们将从基于xfem(扩展有限元法)的角度出发,探讨垂直于双材料界面的裂纹扩展问题,以期为这一领域的研究和实际应用提供新的思路和方法。
一、概述垂直于双材料界面的裂纹扩展问题是指在两种材料的交界面上,裂纹在垂直方向上的扩展行为。
这种情况下,裂纹扩展的受力和受约束条件都受到了双材料特性的影响,需要深入分析和研究。
传统的有限元法在模拟和分析这种问题时存在一定的局限性,而xfem则能够有效地刻画裂纹的扩展路径和受力情况,因此成为了研究这一问题的有力工具。
二、裂纹模型的建立在进行垂直于双材料界面的裂纹扩展问题建模时,需要考虑双材料界面的影响,分析裂纹在材料间传播的受力情况和速度。
利用xfem,可以方便地将裂纹扩展路径和扩展速度等参数纳入模型中,通过数值计算得到裂纹扩展的演化规律和裂纹尖端的受力情况。
这有助于更准确地理解和分析垂直双材料界面上的裂纹扩展问题。
三、影响因素分析垂直于双材料界面的裂纹扩展受到诸多因素的影响,其中包括材料性质、裂纹尺寸、应力状态等。
通过xfem的数值模拟,可以分析不同因素对裂纹扩展行为的影响程度,揭示裂纹扩展过程中的关键因素和规律。
这有助于为材料设计和工程应用提供更可靠的参考依据。
四、工程应用与展望垂直于双材料界面的裂纹扩展问题在工程应用中具有重要意义,例如在复合材料结构的设计和评估中。
通过对裂纹扩展行为的深入研究和分析,可以为工程实践提供更有效的裂纹控制和结构安全性评估方法。
未来,基于xfem的裂纹扩展问题研究还可以结合人工智能算法和大数据分析等方法,进一步提高模型精度和计算效率,拓展应用领域和深化理论研究。
个人观点与总结垂直于双材料界面的裂纹扩展问题是一个复杂而又具有挑战性的研究领域,需要运用先进的数值模拟方法和理论分析手段来探讨和解决。
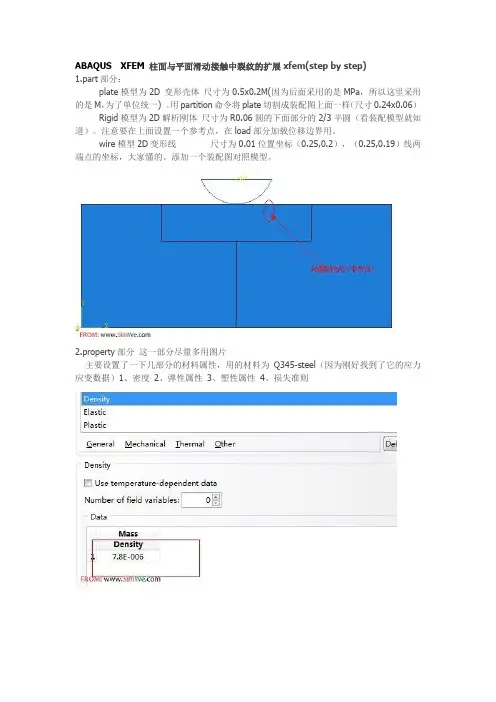
ABAQUS XFEM 柱面与平面滑动接触中裂纹的扩展xfem(step by step)
1.part部分:
plate模型为2D 变形壳体尺寸为0.5x0.2M(因为后面采用的是MPa,所以这里采用的是M,为了单位统一) 。
用partition命令将plate切割成装配图上面一样(尺寸0.24x0.06)Rigid模型为2D解析刚体尺寸为R0.06圆的下面部分的2/3半圆(看装配模型就知道)。
注意要在上面设置一个参考点,在load部分加载位移边界用。
wire模型2D变形线尺寸为0.01位置坐标(0.25,0.2),(0.25,0.19)线两端点的坐标,大家懂的。
添加一个装配图对照模型。
2.property部分这一部分尽量多用图片
主要设置了一下几部分的材料属性,用的材料为Q345-steel(因为刚好找到了它的应力应变数据)1、密度2、弹性属性3、塑性属性4、损失准则
5.interaction部分
1.首先创建contact controls,创建步棸菜单栏interaction->contact controls->create,参数的设置见下图:
2.裂纹的设置,创建步棸菜单栏special->crack->create->xfem ,区域的选择见下图
3其他包括相互作用的一些属性见下图
6.load部分
位移边界条件的加载如下图
7.Mesh部分
种子布置见下图
网格控制主要采取的是structured
8.Job就ok了,祝大家好运。
也同时感谢论坛里面帮助过我的朋友。


扩展有限元方法和裂纹扩展1.1 扩展有限元方法(XFEM )基本理论1999年,美国Northwestern University 的Belytschko 和Black 领导的研究小组提出了扩展有限元方法,为解决裂纹这类强不连续问题带来了曙光。
他们正式应用扩展有限元法(XFEM )这一专业术语是在2000年,截止到目前,扩展有限元法(XFEM )成为我们解决强不连续力学问题的最有效的数值计算方法,也成为计算断裂力学的重要分支。
XFEM 在有限元的框架下进行求解,无需对构件内部的物理界面进行网格划分,具有常规有限元方法的所有优点。
它最明显的特点是用已知的特征函数作为形函数来使传统有限元的位移得到逼近,进而克服了在裂纹尖端和变形集中处进行高密度网络划分产生的困难,方便地模拟裂纹的任意路径,而且计算精度和效率得到了显著的提高[6]。
扩展有限元方法是将已知解析解的特征函数作为插值函数增强传统有限元的位移逼近,来使得单元内的真实位移特性得以体现,裂纹尖端和物理或几何界面独立于有限元网格。
XFEM 主要包括以下三部分内容:首先是不考虑构件的任何内部细节,按照构件的几何外形尺寸生成有限元网格;其次,采用水平集方法跟踪裂纹的实际位置;根据已知解,改进影响区域的单元的形函数,来反映裂纹的扩展。
最后通过引入不连续位移模式来表示不连续几何界面的演化。
因为改进的插值函数在单元内部具有单元分解的特性,其刚度矩阵的特点与常规有限元法的刚度矩阵特性保持一致。
单元分解法(Partition Of Unity Method)和水平集法(Level Set Method )、节点扩展函数构成了扩展有限元法的基本理论,其中,单元分解法是通过引入加强函数计算平面裂纹扩展问题,保证了XFEM 的收敛性;水平集法是跟踪裂纹的位置和模拟裂纹扩展的常用数值方法,任何内部几何界面位置都可用它的零水平集函数来表示。
(1)单元分解法的基本思想是任意函数()x φ都可以用子域内一组局部函数()()x x N I ϕ表示,满足如下等式:()()()x x N x II ϕφ∑= (1)其中,它们满足单位分解条件:f I Iåx ()=1 ()x N I 是有限元法中的形函数,根据上述理论,便可以根据需要对有限元的形函数进行改进。


基于ABAQUS平台的扩展有限元方法断裂是一种失效模式。
在工程领域中,经常发生起源于断裂或终结于裂纹扩展的灾难性破坏事故,如压力管道的裂纹失稳扩展,机械构件的断裂,地震引起的地面开裂和房屋倒塌等,这些事故对我们的生命和生活造成了很大的影响。
由于产生裂纹的原因难以量化,因此裂纹出现后是否会继续扩展或发生止裂的断裂力学具有很重要的意义。
传统的断裂力学在剖分单元网格的时候必须考虑物体内部的缺陷,如裂纹,界面等,使单元边界与几何界面一致,这也就会形成局部网格加密,而其余区域稀疏的非均匀网格分布。
ABAQUS中单元的最小尺寸决定了显示计算时间增量的临界步长,过小的最小尺寸无疑会增加计算的成本;再有就是需要预先给定裂纹的扩展路径,裂纹只能沿单元边界扩展,难以形成任意裂纹路径。
扩展有限元方法(XFEM,extended finite element method,以下简称XFEM)的核心思想是用扩充的带有不连续性质的形函数基来代表计算域内的间断,因此在计算过程中,不连续场的描述完全独立于网格边界,这使其在处理断裂问题上具有很大的优势。
XFEM可以充分利用已知解析解答构造形函数基,在较粗网格上即能得到较精确的解答。
利用XFEM,还可以方便地模拟裂纹沿任意路径扩展。
ABAQUS中的XFEM可以用来研究裂纹的产生及模拟沿任意路径的裂纹扩展,而无需对模型进行网格重构。
XFEM可以用于三维实体模型、二维平面模型,不能用于三维的壳模型。
ABAQUS在Interaction模中定义XFEM裂纹,可以指定裂纹的初始位置,也可以不指定,让ABAQUS在分析过程中根据计算断裂区域的最大初始应力或应变确定裂纹的位置。
在ABAQUS中执行XFEM断裂分析,必须指定:断裂区域,裂纹生长(可选),裂纹初始位置(可选),富集半径,接触交互属性,损伤起始准则和分析类型,如静态分析,或隐式动态分析。
下面以一个例子演示ABAQUS中使用XFEM方法对平板中的边缘裂纹进行动态裂纹扩展预测。

使用X-FEM方法建立间断化扩展特性概述建立离散化扩展特性,如裂纹:●通常被称为扩展有限元方法(XFEM);●基于单元划分的传统有限元方法扩展;●采用特殊的位移函数,通过扩展自由度允许间断特性的存在;●不需要重新划分网格用于适应几何间断特性;●是一种非常有效和有吸引力的方法,用于模拟任意性、求解相关路径裂纹的裂纹初始及裂纹扩展过程,而不用要求重新划分网格;●可以同时与基于面的粘性行方法(surface-based cohesive behavior)和虚拟裂纹闭合法同时使用(VCCT);●可以用于计算任意稳定表面裂纹的路径积分,而不需要在裂纹尖端周围重新剖分网格;●允许基于小滑动形式(small-sliding formulation)的裂纹单元之间的接触作用;●允许几何非线性和材料非线性的存在;●当前只对一阶应力/位移固体连续单元有效。
建模方法使用传统有限元方法建立固定不连续性质,如裂纹,要求网格划分符合几何不连续。
因此,很多的网格重构需要建立用以更好地模拟裂纹尖端附近奇异渐进场。
建立扩展裂纹模型更加复杂,这是由于网格需要连续不断地更新以适应裂纹扩展过程中几何不连续性。
扩展有限元方法(XFEM)可以缓解裂纹面网格划分带来的缺点。
扩展有限元方法由Belytschko and Black(1999)首次提出。
该方法基于整体划分(partition of unity)的概念(Melenk and Babuska 1996),属于传统有限元方法的扩展。
该整体划分概念使扩展函数(enrichment functions)方便地插入到有限元近似当中。
间断性可以通过与额外自由度相关联的扩展函数(enriched functions)来确定。
然而,扩展有限元方法保留了有限元框架及一些特性,如刚度矩阵的稀疏性及对称性等。
节点扩展函数简介(Introducing nodal enrichment functions)为了实现断裂分析,扩展函数通常包括裂纹尖端附近渐进函数(near-tip asymptotic functions)-用于模拟裂纹尖端附近的应力奇异性,及间断函数(discontinuous functions)-用于表示裂纹面处位移跳跃。

热腐蚀疲劳裂纹扩展有限元模拟概述说明以及解释1. 引言1.1 概述热腐蚀疲劳是金属材料在高温和腐蚀环境中长期使用过程中发生的一种疲劳现象。
在这种条件下,材料会受到复杂的力学、化学和热耦合作用,导致裂纹的产生和扩展。
因此,对于热腐蚀疲劳和裂纹扩展机制进行深入的研究具有重要意义。
1.2 文章结构本文将分为三个部分进行讨论,首先会对热腐蚀疲劳进行概述说明,包括其产生原因、影响因素等内容;然后将解释裂纹扩展机制,阐述不同环境条件下裂纹扩展行为的特点;最后介绍有限元模拟在热腐蚀疲劳中的应用,并探讨其优缺点以及未来发展方向。
1.3 目的本文旨在全面了解和阐述热腐蚀疲劳、裂纹扩展机制以及有限元模拟在该领域中的应用。
通过对已有文献和实验结果的综合分析,探讨热腐蚀疲劳对材料性能和工程结构寿命的影响,并为相关领域的进一步研究提供参考和展望。
2. 正文:2.1 热腐蚀疲劳概述说明:热腐蚀疲劳是指在高温和腐蚀介质中,材料发生的由于循环载荷引起的疲劳断裂现象。
它是一种常见的工程问题,广泛存在于航空、能源等领域。
热腐蚀疲劳具有复杂的损伤机制,包括氧化、腐蚀、应力诱导等多个因素相互作用所导致的材料失效。
2.2 裂纹扩展机制解释:裂纹扩展是热腐蚀疲劳过程中的一项重要现象。
在循环载荷作用下,由于应力集中或缺陷存在,材料表面产生微小裂纹。
随着时间和循环次数的增加,这些微小裂纹会逐渐扩展并相互连通,最终导致材料失效。
裂纹扩展受到多个因素影响,如应力水平、温度、腐蚀介质以及材料本身的力学性能等。
2.3 有限元模拟在热腐蚀疲劳中的应用:有限元模拟是一种常用的工程分析方法,可以应用于热腐蚀疲劳相关问题的研究。
通过建立适当的数学模型、物理方程和边界条件,有限元模拟可以在计算机上模拟材料在不同工况下的响应行为。
在热腐蚀疲劳中,有限元模拟可以用来预测材料的失效寿命、裂纹扩展速率以及评估其结构的可靠性。
有限元模拟在热腐蚀疲劳中的应用主要包括以下几个方面:首先,通过建立材料力学性能及裂纹扩展规律等方面的数学模型,可以使用有限元模拟来预测热腐蚀疲劳过程中裂纹扩展的发展趋势和速率。

使用X-FEM方法建立间断化扩展特性 概述 建立离散化扩展特性,如裂纹: 通常被称为扩展有限元方法(XFEM); 基于单元划分的传统有限元方法扩展; 采用特殊的位移函数,通过扩展自由度允许间断特性的存在; 不需要重新划分网格用于适应几何间断特性; 是一种非常有效和有吸引力的方法,用于模拟任意性、求解相关路径裂纹的裂纹初始及裂纹扩展过程,而不用要求重新划分网格; 可以同时与基于面的粘性行为方法(surface-based cohesive behavior)和虚拟裂纹闭合法同时使用(VCCT); 可以用于计算任意稳定表面裂纹的路径积分,而不需要在裂纹尖端周围重新剖分网格; 允许基于小滑动形式(small-sliding formulation)的裂纹单元之间的接触作用; 允许几何非线性和材料非线性的存在; 当前只对一阶应力/位移固体连续单元有效。 建模方法 使用传统有限元方法建立固定不连续性质,如裂纹,要求网格划分符合几何不连续。因此,很多的网格重构需要建立用以更好地模拟裂纹尖端附近奇异渐进场。建立扩展裂纹模型更加复杂,这是由于网格需要连续不断地更新以适应裂纹扩展过程中几何不连续性。 扩展有限元方法(XFEM)可以缓解裂纹面网格划分带来的缺点。扩展有限元方法由Belytschko and Black(1999)首次提出。该方法基于整体划分(partition of unity)的概念(Melenk and Babuska 1996),属于传统有限元方法的扩展。该整体划分概念使扩展函数(enrichment functions)方便地插入到有限元近似当中。间断性可以通过与额外自由度相关联的扩展函数(enriched functions)来确定。然而,扩展有限元方法保留了有限元框架及一些特性,如刚度矩阵的稀疏性及对称性等。 节点扩展函数简介(Introducing nodal enrichment functions) 为了实现断裂分析,扩展函数通常包括裂纹尖端附近渐进函数(near-tip asymptotic functions)-用于模拟裂纹尖端附近的应力奇异性,及间断函数(discontinuous functions)-用于表示裂纹面处位移跳跃。使用整体划分特性的位移向量函数u表示为 其中为常用的节点位移形函数;上述公式中等号右边第一项代表有限元位移求解对应的连续部分;第二项为节点扩展自由度向量,为沿裂纹面的间断跳跃函数;第三项为节点扩展自由度向量,为裂纹尖端应力渐进函数。右端第一项可用于模型中所有节点;右端第二项只对形函数被裂纹内部切开的单元节点有效;右端第三项只对形函数被裂纹尖端切开的单元节点有效。

2019年18期创新前沿科技创新与应用Technology Innovation and Application扩展有限元法在疲劳裂纹扩展模拟中的应用张芮晨(中国直升机设计研究所,天津300000)前言目前,有限元仿真大量应用于疲劳问题分析计算中。
然而常规有限元法采用连续函数作为形状(插值)函数,在单元内部形状函数和材料性能必须保证连续,进行裂纹分析时,裂纹面需与网格边界重合,网格节点需与间断面的尖端重合[1-2]。
如Abaqus 中针对裂纹扩展分析的两种技术:基于debond 裂纹扩展技术和基于cohesive 裂纹扩展技术。
两种技术均需提前指定裂纹扩展区域与方向,对于网格的划分限制较大,工作量大,效率低。
而在扩展有限元法(Extended Finite Element Method ,XFEM )中,网格与结构内部的几何或物理界面无关,两者间相互独立,裂纹尖端应力场的计算与裂纹面扩展计算相互独立,避免了在裂纹尖端进行高密度网格划分的问题和网格重新划分的工作[3-5]。
本文采用扩展有限元法对疲劳裂纹扩展进行仿真分析,达到无需指定裂纹扩展路径、无需进行高密网格划分也可模拟裂纹扩展的目的,节省建模所需要的时间,大大减少工作量,同时又提高了裂纹扩展模拟的准确度。
1扩展有限元法理论基础1.1单位分解法(PUM )扩展有限元通过在常规有限元位移模式中加进跳跃函数和渐进裂尖位移场函数等一些特殊的函数,来有效地模拟类似裂纹一类的强不连续问题,而它的理论基础既为单位分解法。
在单位分解法中,认为任何函数φ(x)都可以用域内局部函数H Γ(x)φ(x)表示,即其中,H Γ(x)为有限单元形状函数,它形成一个单位分解(2)以此为基础,对有限元形状函数进行改进。
重叠分片{θi }构成研究区域M 的一个覆盖,{φi }为覆盖上的一个单位分解。
在每一分片上,函数空间V i 为区域M 的局部逼近,总体试探空间V 为(3)总体空间V 不但具有局部空间V i 的逼近特性,又有单位分解φi 和局部空间V i 的光滑性,只要单位分解φi 足够光滑,就能构造出足够光滑的试探空间。
冲击作用下混凝土裂纹扩展机理的有限元模拟一、引言在土木工程领域中,混凝土裂纹扩展是一个非常重要的问题。
由于混凝土的性质和结构,混凝土在受到冲击或其他外力作用时容易产生裂纹。
裂纹的扩展会对混凝土的强度和耐久性产生影响,进而影响工程的安全性和使用寿命。
因此,研究混凝土裂纹扩展机理对于提高混凝土结构的安全性和耐久性具有重要意义。
二、混凝土裂纹扩展机理混凝土在受到冲击作用时,由于混凝土的韧性和延性较差,容易发生裂纹。
混凝土裂纹扩展的机理可以分为两个方面:一是受力分布不均匀,导致裂纹的产生和扩展;二是混凝土的损伤累积效应,使得裂纹的扩展更加容易。
1. 受力分布不均匀引起的裂纹产生和扩展混凝土在受到外力作用时,由于混凝土的强度和韧性不均匀,所以外力作用的分布也是不均匀的。
在受力分布不均匀的情况下,混凝土中会产生应力集中的现象,这会导致混凝土中出现裂纹。
随着外力的不断作用,裂纹会逐渐扩展,直到混凝土失去承载能力。
2. 混凝土的损伤累积效应混凝土在受到外力作用时,由于混凝土中的微小缺陷和裂纹,会导致混凝土的损伤。
随着外力的不断作用,混凝土中的损伤会逐渐累积,这会使得混凝土的强度和韧性逐渐降低。
当混凝土的强度和韧性降低到一定程度时,混凝土中的裂纹会开始扩展,直到混凝土失去承载能力。
三、有限元模拟分析有限元模拟是一种常用的工程计算方法。
通过建立模型,将实际的物理问题转化为数学问题,利用计算机进行计算和模拟,得到物理问题的解。
在混凝土裂纹扩展机理的研究中,有限元模拟可以帮助我们分析混凝土受力分布、应力集中、裂纹扩展等问题,从而得出混凝土裂纹扩展的机理。
1. 模型建立建立混凝土裂纹扩展的有限元模型需要考虑多个因素,如混凝土的材料性质、外力作用的方式和强度、裂纹的形态和扩展方向等。
在建立模型时,需要对这些因素进行合理的假设和模拟,以保证模型的可靠性和准确性。
2. 受力分析在有限元模拟中,需要对混凝土受到的外力进行分析。
外力的大小、方向和作用时间等都会对混凝土的裂纹扩展产生影响。
基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常见的传动装置,它由若干个相互连接的膜片组成。
在工作过程中,膜盘联轴器通常承受着较大的转矩和转速,在长时间的工作过程中,可能会出现裂纹扩展的问题。
为了对膜盘联轴器的裂纹扩展进行模拟分析,可以采用基于扩展有限元法(XFEM)的方法。
XFEM是一种能够建模材料内部裂纹扩展的有限元方法。
与传统的有限元方法相比,它能够准确地模拟裂纹的扩展行为,为工程师提供更加准确的断裂分析结果。
在膜盘联轴器的裂纹扩展模拟中,首先需要将裂纹引入到模型中。
由于膜盘联轴器是由多个膜片组成的,因此裂纹通常会发生在膜片之间的接头处。
引入裂纹后,需要对裂纹进行离散化,将裂纹划分为许多小的单元,以便进行有限元分析。
在裂纹扩展过程中,裂纹尖端会受到应力场的影响,从而导致裂纹扩展。
为了模拟这个过程,需要在有限元分析中引入裂纹扩展准则。
常用的裂纹扩展准则包括J-integral准则和应力强度因子准则。
通过这些准则,可以根据应力和应变场的变化来判断裂纹是否会继续扩展。
在裂纹扩展模拟中,使用XFEM可以有效地模拟裂纹的扩展行为。
XFEM采用了分片形函数的方法,能够在裂纹尖端的元素上引入裂纹影响函数,从而准确地模拟裂纹扩展过程。
与传统的有限元方法相比,XFEM能够更加准确地预测裂纹的扩展路径和扩展速率。
通过基于XFEM的膜盘联轴器裂纹扩展模拟,可以得到裂纹扩展的路径和速率,为工程师提供了重要的参考数据。
这对于设计更可靠的膜盘联轴器、预测其寿命和提高其工作性能具有重要意义。
还可以通过模拟分析来指导维修和保养过程,及时发现和修复潜在的裂纹问题,确保膜盘联轴器的正常运行。
基于XFEM的膜盘联轴器裂纹扩展模拟膜盘联轴器是一种常用的机械传动装置,其主要用于传递两个轴的转矩。
在使用过程中,由于工作条件的复杂性以及材料的疲劳,裂纹的形成和扩展是不可避免的。
对膜盘联轴器裂纹扩展行为的研究具有重要的意义。
基于扩展有限元法(XFEM),可以模拟材料中裂纹的扩展行为。
XFEM是一种将数值分析方法与数学基础理论相结合的仿真方法。
通过加入扩展刚度场(ESF)和裂缝增长准则,XFEM可以模拟裂纹的扩展路径和速率。
需要建立膜盘联轴器的几何模型,并进行网格划分。
膜盘联轴器通常由圆盘和薄膜组成,所以在建模时需要考虑这两者的几何形状和尺寸。
对于圆盘部分,可以使用二维或三维的几何模型,而薄膜部分可以使用二维的模型。
接下来,需要定义材料的物理性质。
膜盘联轴器通常由金属材料制成,所以可以使用弹塑性或弹性模型来描述材料的力学行为。
还需要考虑到裂纹的存在,因此还需要定义裂纹初始位置和几何形状。
在建立模型和定义物理性质之后,可以进行裂纹扩展的模拟。
需要通过裂纹模式函数来描述裂纹的形状。
裂纹模式函数通常具有能量的形式,可以通过求解裂纹模式函数的极小值问题来确定裂纹的形状。
接着,需要定义扩展刚度场(ESF)。
ESF是一种包含了裂纹信息的场,用于模拟裂纹的扩展行为。
ESF可以根据裂纹的位置和形状被构建出来,并被添加到原始的有限元方程中。
通过裂纹增长准则来决定裂纹的扩展路径和速率。
裂纹增长准则通常基于能量释放率或位移场,在每个时间步中,通过计算裂纹增长准则来确定裂纹的扩展行为。
基于XFEM的膜盘联轴器裂纹扩展模拟可以提供有关裂纹形成和扩展行为的重要信息。
通过模拟,可以研究不同参数和工况对裂纹扩展的影响,为膜盘联轴器的设计和寿命评估提供依据。
该模拟方法还可以应用于其他材料和结构的裂纹扩展研究中。
扩展有限元在混凝土裂缝问题研究中的应用本文通过扩展有限元模拟了工程中大体积混凝土裂缝形成以及发展过程,为研究大体积混凝土工程中的裂缝控制问题提供了理论依据。
1 概述水利水电工程在经济发展中起了重要的作用,同时由于自身的安全特性导致了建筑物的溃坝事故的发生,给相关工程的当地人民带来了安全隐患。
在这些问题中,一部分安全隐患主要是由于混凝土的裂缝导致的,在大体积混凝土工程中,裂缝决定着工程的成功与否以及使用寿命。
混凝土裂缝的成因主要可以分为两类:1、外部因素,可以简单的概括为荷载,例如自重、水压力、温度以及动力荷载等因素的影响;2、内部因素,主要是混凝土材料的强度指标的大小、时效性、区域性等等。
目前对于内部因素,国内外研究的成果在工程中得到了广泛的应用,而对于外部因素如何影响混凝土裂缝的产生以及发展的研究,在工程中的应用不足。
本文利用国内外最新的数值计算方法,来讨论混凝土裂缝的发展过程,以期为工程的风险分析提供一种更为准备的数值计算手段。
2 扩展有限元2.1 建模方法使用传统有限元方法建立固定不连续性质,如裂纹,要求网格划分符合几何不连续。
因此,很多的网格重构需要建立用以更好地模拟裂纹尖端附近奇异渐进场。
建立扩展裂纹模型更加复杂,这是由于网格需要连续不断地更新以适应裂纹扩展过程中几何不连续性。
扩展有限元方法(XFEM)可以缓解裂纹面网格划分带来的缺点。
扩展有限元方法由Belytschko and Black(1999)首次提出。
该方法基于整体划分的概念(Melenk and Babuska 1996),属于传统有限元方法的扩展。
该整体划分概念使扩展函数方便地插入到有限元近似当中。
间断性可以通过与额外自由度相关联的扩展函数来确定。
然而,扩展有限元方法保留了有限元框架及一些特性,如刚度矩阵的稀疏性及对称性等。
XFEM已经在通用的有限元程序ABAQUS中实现,本文以ABAQUS平台,利用XFEM来模拟大体积混凝土裂缝的开裂及扩展。
基于ABAQUS 扩展有限元的裂纹模拟化工过程机械622080706010 李建1 引言1.1 ABAQUS 断裂力学问题模拟方法在abaqus中求解断裂问题有两种方法(途径):一种是基于经典断裂力学的模型;一种是基于损伤力学的模型。
断裂力学模型就是基于线弹性断裂力学及其基础上发展的弹塑性断裂力学等。
如果不考虑裂纹的扩展,abaqus可采用seam型裂纹来分析(也可以不建seam,如notch型裂纹),这就是基于断裂力学的方法。
这种方法可以计算裂纹的应力强度因子,J积分及T-应力等。
损伤力学模型是指基于损伤力学发展而来的方法,单元在达到失效的条件后,刚度不断折减,并可能达到完全失效,最后形成断裂带。
这两个模型是为解决不同的问题而提出来的,当然他们所处理的问题也有交叉的地方。
1.2 ABAQUS 裂纹扩展数值模拟方法考虑模拟裂纹扩展,目前abaqus有两种技术:一种是基于debond的技术(包括VCCT);一种是基于cohesive技术。
debond即节点松绑,或者称为节点释放,当满足一定得释放条件后(COD 等,目前abaqus提供了5种断裂准则),节点释放即裂纹扩展,采用这种方法时也可以计算出围线积分。
cohesive有人把它译为粘聚区模型,或带屈曲模型,多用于模拟film、裂纹扩展及复合材料层间开裂等。
cohesive模型属于损伤力学模型,最先由Barenblatt 引入,使用拉伸-张开法则(traction-separation law)来模拟原子晶格的减聚力。
这样就避免了裂纹尖端的奇异性。
Cohesive 模型与有限元方法结合首先被用于混凝土计算和模拟,后来也被引入金属及复合材料。
Cohesive界面单元要服从cohesive 分离法则,法则范围可包括粘塑性、粘弹性、破裂、纤维断裂、动力学失效及循环载荷失效等行为。
此外,从abaqus6.9版本开始还引入了扩展有限元法(XFEM),它既可以模拟静态裂纹,计算应力强度因子和J积分等参量,也可以模拟裂纹的开裂过程。
被誉为最具有前途的裂纹数值模拟方法。
本文将利用abaqus6.9版本中的扩展有限元法功能模拟常见的Ⅰ型裂纹的扩展。
2 Ⅰ型裂纹的扩展有限元分析本文针对断裂力学中的平面Ⅰ型裂纹扩展问题用abaqus中的扩展有限元方法进行数值模拟,获得了裂纹扩展的整个过程,裂尖单元的应力变化曲线,以及裂纹尖端塑性区的形状。
在此基础上绘制裂纹扩展的能量历史曲线变化趋势图。
2.1 平面裂纹的几何模型几何模型的尺寸参数如图1所示,其中a=1.5m,b=3m,L=10m,厚度为1m。
上下两端分别承受25.32MPa的拉力。
图1 裂纹的几何示意图2.2 有限元模型有限元程序采用大型通用ABAQUS6.9软件,选用8节点六面体减缩单元(C3D8R)。
网格划分的模型如图2所示。
图2 网格图2.3 材料性能在有限元分析中假定材料为理想线弹性的,弹性模量E为2.1×105MPa,泊松比为0.3。
本文采用的是基于损伤力学演化的失效准则。
具体的参数设置如下。
损伤判据为最大主应力失效准则作为损伤起始的判据,最大主应力为84.4MPa。
损伤演化选取基于能量的、线性软化的、混合模式的指数损伤演化规律,有关参数为G1C= G2C= G3C=42200N/m,α=1。
2.4 边界条件和初始条件对于含有裂纹的平板,我们仅仅需要约束住它的刚体位移,保证在在平板两个断面施加应力载荷时,平板不会出现意外的刚体运动。
设置裂纹类型为扩展有限元裂纹,扩展区域是整个平板,扩展路径为任意路径。
由于计算裂纹扩展实际上是一个大变形问题,所以分析步骤的几何非线性一定要打开。
由于裂纹扩展本身是一个强烈的非连续问题,它将导致求解过程的迭代有可能出现不收敛的情况,另外,求解的增量步也会要求很小,这会导致求解时间很长。
因此非常有必要对求解过程做一些参数控制,以避免迭代不收敛导致的求解失败的情况的出现。
图3 裂纹体及其扩展区域图4 载荷及边界条件3 结果分析3.1 静态裂纹的应力强度因子及J积分的验证计算应力强度因子及J积分时,需要设置裂纹不能扩展,从而计算静态裂纹的应力强度因子,同时还要在历史变量输出中做相关的设置。
另外分析步也需要将几何非线性去除,因为裂纹没有扩展。
由此计算得到了裂尖在25.32MPa载荷下的Ⅰ型应力强度因子。
同时,我们根据断裂力学理论中关于此模型的理论解如公式(1),计算理论的应力强度因子。
最后得到的结果列于表1。
⎪⎭⎫⎝⎛=I b a F a K πσ (1)上式中a ,b 分别是裂纹体的几何尺寸,F 为关于a 和b 比值的函数,可以查表得到,本文中a 与b 的比值为0.5,查表得到F 的函数值为1.50。
表1 应力强度因子的对比表本文计算值 理论计算值 )(2/1m MPa K ⋅I58.6958.28由此可以计算相对误差为:1.06%,此误差显然属于5%的允许误差范围之内。
所以本文计算得到的应力强度因子是可信的。
此外,本文还利用此模型计算了静态裂纹的J 积分值,由于材料是理想线弹性的,所以J 积分与应力强度因子之间存在这样关系,如公式(2)。
EK J 2I = (2)本文在这里列出J 积分的变化趋势图,图中对比了公式(2)的理论解以及有限元结果。
从图中可以看出,两者是吻合的,说明了有限元模拟是正确的。
J 积分随加载的变化趋势图如图5所示。
红色实线表示的是理论结果,黑色点表示有限元结果。
0.02.0x1034.0x1036.0x1038.0x1031.0x1041.2x1041.4x1041.6x1041.8x104J 积分/N m -1Step time图5 J 积分历史曲线图3.2 裂纹扩展过程展示Step time=0.1143 Step time=0.3943 Step time=0.6743 Step time=0.7976 Step time=0.8708 Step time=0.9551Step time=0.9994 Step time=0.9998 Step time=1图6 裂纹扩展过程从上述的裂纹扩展过程的应力分布图,我们可以得到如下几点结论,证明我们的数值模拟具有一定的正确性。
首先,在裂纹尖端出现了应力集中,这是和断裂力学理论符合的。
其次,观察裂纹附近的应力分布,我们可以看到应力分布的趋势是与理论计算的塑性区的形状大致相同的,理论计算的塑性区形状如图7所示。
图7 理论上的塑形区形状图3.3 裂尖单元应力变化其次,考察裂尖单元的应力随载荷增加的变化。
实际上裂尖单元应力值的具体大小并没有意义,因为表征断裂韧强度的是应力强度因子和J 积分。
而单元应力随载荷增加导致的变化可以帮助我们理解裂尖单元在起裂到完全断裂的整个过程。
观察图8,我们可以大致得到这个裂尖单元参与断裂过程的整个历史。
首先,在应力加载的早些时候,裂尖单元的应力随着载荷的增加而增加,此时裂尖单元的应力并没有达到损伤判据的临界应力,所以单元没有起裂。
随着载荷的继续增加,应力值继续增加,当到大概0.7976左右时,裂尖的最大主应力达到了最大主应力损伤判据的临界值,于是裂纹起裂,直至完全裂开,单元的应力奇异性消失,裂尖单元转变为一个普通的非裂尖单元。
这个过程对应于图8中的右边应力增大后有急剧减小的曲线。
之后,由于载荷还没有完全加载完毕,所以裂尖单元在转变为普通单元之后随着载荷的继续增加,其单元应力又会随之在增加。
以上就是一个裂尖单元在整个加载过程中的单元应力历史变化的三个阶段。
最大主应力/M P aStep time图8 裂纹尖端单元应力历史曲线3.4 裂纹扩展分析如图9所示,载荷从零开始不断加载。
随着载荷的增加,裂尖处的单元应力也不断增加。
当裂尖处的最大主应力值达到临界值时,裂尖处的单元开始失效,裂纹开始穿过单元扩展,时间步大概是0.7976左右,此时裂尖处开始形成粘结裂纹(cohesive crack)。
从0-0.7976这个过程可以认为是裂纹孕育期。
之后随着裂尖处的能量释放率达到裂纹扩展阻力率G C 时,裂尖处的粘结裂纹开始扩展成真实裂纹,裂尖单元的XFEM值达到1。
裂尖处的单元损伤值达到临界值,时间步大概是0.9996左右。
此时认为这一结构开始失效,裂纹失去平衡,开始失稳扩展,真实裂纹开始形成并不断扩展。
从0.7976-0.9996这个过程可以认为是裂纹的萌生过程。
0.9996以后裂纹失稳扩展,结构失效。
从图中可以看出初始裂纹长度为12个单元距离,到最终加载结束时,真实裂纹长度为15个单元长度,粘结裂纹长度为7个单元长度。
图9 随加载历史扩展的动态裂纹图3.5 裂纹扩展的能量历史曲线绘出整个模型的总能量,动能,内能和外力功随计算过程的历史曲线如图10所示。
由图可以看出,总能量和动能在整个过程中并没有发生显著的增加,可以表明整个计算过程基本是稳定的。
而伪应变能在计算过程中有稍微的增长。
-1x101x102x103x104x105x106x107x108x109x10能量/N m -1Step time图10 裂纹扩展的能量历史曲线4 结论本文的工作是基于abaqus6.9版本的扩展有限元功能计算了Ⅰ型裂纹的扩展。
得到如下几点结论。
首先,本文计算了Ⅰ型裂纹的应力强度因子,结构表明计算值与理论值的误差在5%以内,结果可靠有效。
同时计算了裂纹的J 积分值,获得了J 积分的历史曲线,有限元结果与理论结果吻合。
裂纹的扩展过程与理论是吻合的,整个裂纹扩展的计算没有出现不稳定的情况。
裂尖出现了应力的奇异性,裂纹扩展平稳。
并通过研究裂尖单元的应力历史曲线,直观的获得了裂纹在一个单元上扩展的三个典型阶段。
其次,对裂纹扩展的过程进行了分析,指出了裂纹扩展的大概几个阶段以及具体的裂纹扩展过程。
最后,对裂纹扩展过程中的能量变化作了简单描述,说明了计算过程的稳定性,并验证了系统的能量守恒关系。