位置度公差及其计算解释介绍

格式：pdf
大小：1.09 MB
文档页数：48

下载文档原格式

位置度计算

综合
2 – M4X12
Ø T1 M
底座 A
Ø 4.2
+ 0.2 0
盖板
2 – Ø 4.2 Ø 4.2
+ 0.2 0
A-A
A
Ø T2 M
A
Ø T1 M
A
Ø T2 M
A
P
L L±ΔL
B-B
10±0.5
B
A
R L±ΔL A
+ 0.2 7.8 0 + 0.2 7.8 0
Ø T3 M
A
R
B
Ø T3 M
设计要求：（1）底座与盖板螺钉连结；（3）R槽能通过ø15轴；
谢谢！
或 T1 = 0.05 ， T2 = 0.03 等。
如：T1 = T2 = 0.04
对称板件（活动紧固件连接）
件1
A
Ø 10 H9
Ø T1 M
+ 0.058 0
Ø 20 H 9
+ 0.052 0
E
件2
A M
Ø 20 d 9
- 0.040 - 0.092
E
A 图 11
Ø 10 d 6
- 0.040 - 0.098
+ 0.12 0
件1
4 - Ø 3.5
0 - 0.12
件2
ØT1 M
ØT2 M
图 12
计算： A）由式 (6) 得： H = F + T1 + T2， 4 = 3.5 + T1+T2 则： T1+T2 = 0.5 如： T1 = T2 = 0.25 或 T1 = 0.2， T2 = 0.3 等。 B）由式 (5) 得：T =（H - F）/2 =（4 – 3.5）/2 = 0.25

位置度公差带的定义、标注和解释_汽车机械基础_[共4页]

第6章几何公差
113
续表
面对基准面的倾斜度公差
公差带为间距等于公差值t 两平行平面所限定的区域。

该两平行平面按给定角度倾斜于基准平面基准平面。

提取（实际）表面应限定在间距等于的两平行平面之间。

该两平行平面按理论正确角度40°倾斜于基准平面
6.2.4 位置度公差带的定义、标注和解释
位置公差是指被测提取要素对已具有确定位置的拟合要素的允许变动量，拟合要素由基准和理论正确尺寸（长度或角度）确定的。

当拟合要素和被测提取要素均为轴线时，为同轴度；当拟合要素和被测提取要素均为轴线，且足够短或为中心点时，为同心度；当拟合要素和被测提取要素为其他要素时，为对称度；其他情况均为位置度公差。

位置公差带的定义、标注和解释如表6-5所示。

表6-5 位置公差带的定义、标注和解释（摘自GB/T 1182—2008）
单位：mm
公差带的定义
标注和解释
点的位置度公差
公差值前加注S φ，公差带为直径等于公差值φt 的圆球面所限定的区域。

该圆球面中心的理论正确位置由基准A 、B 、C 和理论正确尺寸确定
提取（实际）球心应限定在直径等于S φ0.3的圆球面内。

该圆球面的中心由基准A 、B 、C 和理论正确尺寸30、25确定
注：提取（实际）球心的定义尚未标准化。

孔位置度计算公式详解

孔位置度计算公式详解孔位置度是指在一定的公差范围内，孔与相关参考面之间的距离，它是衡量孔位质量的指标之一。

孔位置度计算方式是通过测量孔的实际位置与设计位置之间的偏差来进行的。

孔位置度计算公式在国际标准ISO 1101中有详细规定。

以下是详细解析：1. 孔中心位置与设定位置之间的偏差（DTP）：DTP = S - T其中，S表示测量的孔中心位置，T表示设计的孔中心位置。

2. 孔中心位置偏差绝对值：∑DTP = |DTP1| + |DTP2| + … + |DTPn|其中，|DTP1|表示第一组测量中心位置偏差的绝对值，|DTP2|表示第二组测量中心位置偏差的绝对值，以此类推。

3. 孔位置度：孔位置度（P）= 2 × √ ∑DTP^2孔位置度是孔中心位置偏差的平方和的二次根号的2倍。

这个公式可以使得孔与相关参考面之间的距离变成一个综合的评定值，用来衡量孔位质量。

以上公式是比较直接的计算方法，但在实际应用中存在许多误差和不确定因素，因此衍生了如下的计算公式来更精确地衡量孔位置度：孔大小与公差ΣDTM = |DTM1| + |DTM2| + … + |D TMn|其中，|DTM1|表示第一组测量孔大小偏差的绝对值，|DTM2|表示第二组测量孔大小偏差的绝对值，以此类推。

n组孔中心位置与孔径之间的偏差：|DTG1|，|DTG2|，...，|DTGn|其中，|DTG1|表示第一组测量孔中心位置与孔径之间的偏差的绝对值，|DTG2|表示第二组测量孔中心位置与孔径之间的偏差的绝对值，以此类推。

孔位置度的计算公式如下：孔位置度（P）= { [ ∑DTP^2 + (k1 × ΣDTM)^2 ]^0.5 + (k2 ×ΣDTG)^2 }^0.5其中，k1和k2是可根据实际情况取得的系数。

综上所述，孔位置度计算公式通过测量孔的实际位置和孔径与设计位置和孔径之间的偏差，得出孔位置度的评定值，来衡量孔位质量的好坏。

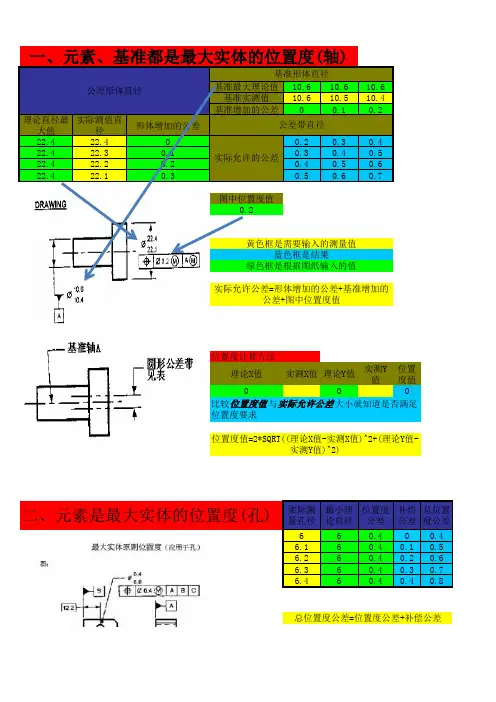
位置度计算公式

基准最大理论值10.610.610.6基准实测值10.610.510.4基准增加的公差00.10.2理论直径最大值实际测值直径形体增加的公差22.422.400.20.30.422.422.30.10.30.40.522.422.20.20.40.50.622.422.10.30.50.60.7图中位置度值0.2理论X值实测X值理论Y值实测Y 值位置度值000实际测量孔径最小理论直径位置度公差补偿公差总位置度公差660.400.46.160.40.10.56.260.40.20.66.360.40.30.76.460.40.40.8一、元素、基准都是最大实体的位置度(轴)基准形体直径公差形体直径公差带直径实际允许的公差位置度计算方法实际允许公差=形体增加的公差+基准增加的公差+图中位置度值位置度值=2*SQRT((理论X值-实测X值)^2+(理论Y值-实测Y值)^2)总位置度公差=位置度公差+补偿公差黄色框是需要输入的测量值蓝色框是结果绿色框是根据图纸输入的值比较位置度值与实际允许公差大小就知道是否满足位置度要求二、元素是最大实体的位置度(孔)位置度值=2*SQRT((理论X值-实测X 值)^2+(理论Y值-实测Y值)^2)位置度值=2*SQRT((理论X值-实测X 值)^2+(理论Y值-实测Y值)^2)总位置度公差=位置度公差+补偿公差基准最小理论值18.118.118.1基准实测值18.218.1518.1基准增加的公差0.10.05理论直径最小值实际测值直径形体增加的公差2525.050.050.350.30.252525.040.040.340.290.242525.020.020.320.270.2225250.30.250.2图中位置度值0.2理论X值实测X值理论Y值实测Y 值位置度值000位置度值=2*SQRT((理论X值-实测X值)^2+(理论Y值-实测Y值)^2)实际允许公差=形体增加的公差+基准增加的公差+图中位置度值位置度计算方法比较位置度值与实际允许公差大小就知道是否满足实际允许的公差公差带直径公差形体直径基准形体直径四、元素、基准都是最大实体的位置度(孔)孔类与轴类的最大最小实体增加的公差区别：轴:最大理论直径－测量直径孔:测量直径－最小理论直径。

位置度的介绍及测量方法-gongkong

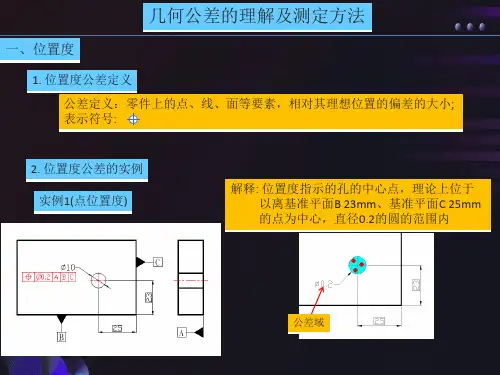
位置度的介绍及测量方法一、位置度的定义是指被测实际要素对其具有理想位置的理想要素的变动量注：理想要素的理想位置由基准和理论尺寸确定（即由几何图框及其位置确定）二、位置度的三要素基准；理论位置值；位置度公差位置度公差带是一以理论位置为中心对称的区域，位置度是限制被测要素的实际位置对理想位置变动量的指标。

它的定位尺寸为理论正确尺寸。

位置度公差在评定实际要素位置的正确性, 是依据图样上给定的理想位置。

位置度包括点的位置度、线的位置度和面的位置度。

点的位置度:如公差带前加S￠，公差带是直径为公差值t的球内的区域，球公差带的中心点的位置由理论正确尺寸确定。

线的位置度：如公差带前加￠，公差带是直径为公差值t的圆柱面内的区域，公差带的轴线的位置由理论正确尺寸确定。

一般来说我们算位置度都是X.Y两个值的偏差量去换算以基准A、B、C建立坐标系，看具体的位置关系选择使用直角或极坐标，一般采用直角坐标，测出被测点到基准的X、Y尺寸，采用公式2乘以SQRT（平方根）（（x2-x1)平方+（y2-y1) 平方）就行，x2是实际尺寸，x1是图纸设计尺寸，计算出的结果就是：实际位置相对于设计的理想位置的偏移量，因为位置度是一个偏移范围￠，所以要乘以2 这个常见的公式三、位置度公差基本原则位置度公差是各实际要素相互之間或它們相对一个或多个基准位置允许的变动全量在位置度公差标注中用理论正确尺寸及位置度公差限制各实际要素相互之間或它們相对一个或多个基准位置,位置度公差相对理想位置为对称分布位置度公差可用于单个的被测要素,也可用于成组的被测要素,当用于成组的被测要素,位置度公差应同时限定成组的被测要素中的每一个被测要素四、位置度公差评定原则最小条件:被测实际要素對理想要素的最大变动量最小五、位置度的评定与测量1、点位置度的测量：其是指包容被测实际点，由基准表面（或）直线和理论正确尺寸确定的定位最小包容区域的直径。

公式：2、线位置度的测量其是指：包容被测实际直线（或轴线）对基准直线（基准面）和理论正确尺寸所确定的定位最小包容的宽度或直径。

位置度公差值数系的理解

位置度公差值数系的理解位置度公差值数系是指在工程设计和制造中，用于描述零件位置精度的一种数值系统。

位置度公差值数系是根据国际标准ISO 1101和国家标准GB/T 1804-2000制定的。

本文将从理解位置度公差值数系的概念入手，介绍其基本原理、应用范围和数值表示方法，并探讨其在工程设计和制造中的重要性和作用。

一、位置度公差值数系的概念位置度公差值数系是一种用于描述零件位置精度的数值系统。

在工程设计和制造中，零件的位置精度是指零件与其它零件之间的相对位置关系。

位置度公差值数系通过定义一组数值来表示零件的位置精度要求，以确保零件在装配和使用过程中能够满足设计要求。

二、位置度公差值数系的基本原理位置度公差值数系的基本原理是基于几何特征和公差要求的匹配关系。

几何特征是指零件的形状、大小和位置等几何性质，公差要求是指零件与其它零件之间的相对位置关系。

位置度公差值数系通过定义一组数值来描述几何特征与公差要求之间的匹配关系，以确保零件在装配和使用过程中能够满足设计要求。

三、位置度公差值数系的应用范围位置度公差值数系广泛应用于各个领域的工程设计和制造中，特别是在精密机械、汽车、航空航天、电子和仪器仪表等行业。

它可以用于描述各种零件的位置精度要求，例如轴、孔、平面、倾斜面、平行度、垂直度、同轴度等。

四、位置度公差值数系的数值表示方法位置度公差值数系使用一组数值来表示零件的位置精度要求。

其中，位置度公差表示零件与其它零件之间的相对位置关系，公差值表示位置度公差的大小。

位置度公差可以分为两种形式，一种是绝对位置度公差，另一种是相对位置度公差。

绝对位置度公差是指零件的位置要求与参考坐标系的位置要求之间的差值，相对位置度公差是指零件之间的相对位置要求。

五、位置度公差值数系在工程设计和制造中的重要性和作用位置度公差值数系在工程设计和制造中具有重要的作用。

首先，它可以确保零件在装配和使用过程中能够满足设计要求，提高产品的质量和可靠性。

几何公差的解释及测定方法

[判定] 1. 平面度大小≤理论值时, 平面度OK ； 2. 平面度大小>理论值时, 平面度NG
[测定实例]
八、直线度
1. 直线度公差定义
公差定义：零件的直线实际形状与理想直线形状的偏差大小表示符号:
2. 直线度公差的实例实例1
解释: 直线度指示的线必须位于距离为公差值0.1mm的两平行直线内
[测定方法] 1. 基准平面A---固定面 2. 基准平面B---基准轴 3. 寸法148的中点---X轴方向的原点 4. 将原点移到寸法 R31的中心位置[X=-19,Y=21,Z=0] 5. 将 R31上任意位置线上多点测定，求得半径与尺寸 R31的差 6. 将原点移到寸法 R41的中心位置[X=90,Y=0,Z=0] 7. 将 R41上任意位置线上多点测定，求得半径与尺寸 R41的差 8. 将原点移到寸法R18的中心位置[X=39,Y=46,Z=0] 9. 将 R18上任意位置线上多点测定，求得半径与尺寸 R18的差 10. 将5&7&9项中Max值与Min值分别求差(即线轮廓度大小)
0.05 A
右侧表面
A
基准平面
0.05
3. 垂直度公差的测量
垂直度的测定
[测定机器] 三次元/百分表
[测定方法] 1. 基准平面A---固定 ; 2. 基准平面B---基准轴 ; 3. 基准平面C---原点 4. 测出垂直度指示面从上端到根部的Max.值/Min.值 5. 计算出Max.值与Min.值的差值(即垂直度大小)
[判定] 1. 垂直度大小≤理论值时, 垂直度OK ； 2. 垂直度大小>理论值时, 垂直度NG
[测定实例]
六、倾斜度
1. 倾斜度公差定义
公差定义：实际的形体相对于保持理论上正确角度的基准直线或基准平面而言偏差的大小

位置公差

4．跳动公差区分： 1）径向圆跳动公差带和圆度公差带 2）径向全跳动公差带和圆柱度公差带 3）端面全跳动公差带和平面度公差带
二、跳动公差
1．圆跳动
斜向圆跳动斜向圆跳动公差带是在以基准轴线为轴线的任一测量圆锥面上，沿其母线方向宽度为圆跳动公差值t的圆锥面区域。
二、跳动公差
1．圆跳动公差
圆跳动测量取各截面（测量圆柱面上）跳动误差的最大值作为该零件的径向（端面）圆跳动误差。
二、跳动公差
1.圆跳动
通常用端面圆跳动控制端面对基准轴线的垂直度误差。例外，当实际端面为中凹或中凸，端面圆跳动误差为零时，端面对基准轴线的垂直度误差并不一定为零。
3．位置度 3.1位置度公差成组要素的位置度2 此位置度公差标注了基准，因此，其几何图框对其它要素的位置是固定的。
一、定位公差
定位公差特点： 1. 定位公差用来控制被测要素相对基准的定位误差。公差带相对于基准有确定的位置。 2. 定位公差带具有综合控制定位误差、定向误差和形状误差的能力。因此，在保证功能要求的前提下，对同一被测要素给出定位公差后，不再给出定向和形状公差。除非对它的形状或（和）方向提出进一步要求，可再给出形状公差或（和）定向公差。
一、定位公差
2．对称度 2.2对称度误差测量对称度误差测量仪器有三坐标测量机、平板和带指示表的表架等。
一、定位公差
3．位置度 3.1位置度公差位置度公差用于控制被测点、线、面的实际位置对其理想位置的位置度误差。理想要素的位置由基准及理论正确尺寸确定。根据被测要素的不同，可分为点的位置度、线的位置度及面的位置度。
二、跳动公差
跳动公差为关联实际被测要素绕基准轴线回转一周或连续回转时所允许的最大变动量。可用来综合控制被测要素的形状误差和位置误差。跳动公差是针对特定的测量方式而规定的公差项目。跳动误差就是指示表指针在给定方向上指示的最大与最小读数之差。

位置度公差

这是本人对于位置度公差的理解过程（或思维过程）的总结，如果大家觉得有价值就参考一下，如果大家觉得没意思，就一笑了之。

还是按习惯分成七步来讲，如果不小心又把大家给讲晕了，那是我的无心之错，敬请谅解。

举个例子也许能弥补一下表达能力的不足：Z-V!R#Xv: z7 O5 Y" _' l; O" v[attachment=25911] Ns'FH(:3 C/ Y) k1 H3 A3 MF?7u~b|@{) ?6 m2 Z% y* Q第一步：确定公差带的大小和形状。

公差带大小及形状是由公差框格中的公差值来确定的，公差值的大小就是公差带的大小，其形状则由公差值有无直径符号来确定，如果公差值前有直径符号，它的公差带就是一个直径等于公差值的圆柱；如果公差值前没有直径符号，它的公差带就应该是相距公差值的两平行平面。

从上面的例子中可以看出，6个φ8的孔的位置度公差带是直径为0.1的圆柱，而4个φ12的孔的位置度公差带是直径为0.2的圆柱。

t-_#Q bzE{ 3 l1 Y6 G! C; F9 w第二步：根据公差带的实体状态修正符号确定补偿公差。

公差带的实体状态由公差值后面的修正符号来确定。

如果没有任何修正符号，则表示位置度公差带在RFS状态，即公差带的大小与被测孔的实际尺寸无关；如果带MMC符号，则表示公差带适用于被测孔在MMC 时，当被测孔的实际尺寸从MMC向LMC偏离时，该偏离量将允许被补偿到位置度公差带上；如果带LMC符号，则表示公差带适用于被测孔在LMC时，当被测孔的实际尺寸从LMC向MMC偏离时，该偏离量将允许被补偿到位置度公差带上。

上图中两个位置度公差均是MMC 状态，因此它们的公差带的大小与被测孔的实际尺寸相关。

比如对φ8的孔来说，当它的实际尺寸在MMC时（φ8），它的位置度要求为φ0.1，当它的实际尺寸在LMC时（φ8.25），它的位置度公差带就变成了φ0.1＋（φ8.25－φ8）＝φ0.35。

位置度公差及其计算89840

位置度公差及其计算89840
• 2.孔组位置度公差的基本标注方法满足第一种设计要求的位置度公差注法 • （1）矩形布置孔组。图6-6。
位置度公差及其计算89840
• （2）圆周布置孔组。图6-5。
位置度公差及其计算89840
• 2.孔组位置度公差的基本标注方法满足第二种设计要求的位置度公差注法 • （1）矩形布置孔组。 • ①复合位置度公差注法：指将孔组的两种位置度公差分别
位置度公差及其计算89840
• 1. 孔组内各孔位置度公差的计算 • 孔组内各孔的位置度公差带计算公式由紧固件与被连接零
件的连接方式决定。 • 通孔连接方式：用螺栓、销钉等紧固件穿过两个或几个被
连接零件上的通孔； • 螺孔连接方式：把双头螺柱、螺钉等紧固件拧入一个被连
接零件的螺孔中，且穿过其余的被连接零件上的通孔。 • （1）通孔连接方式的位置度公差计算（图6-14）
• 孔组应平行于一个侧面的注法，见图6-9。
位置度公差及其计算89840
• （2）圆周布置孔组。 • ①基准孔尺寸公差与被测孔位置度公差的关系采用最大实
体要求：图6-10。 • ②不规定孔组在零件上的确定位置：图6-11、6-12。
• 图6-11所示的爪形扳手上的四销组内四个销只要求能够分别插入螺纹堵盖上的四孔组内四个孔中，可以施力，但不要求它们的端面贴合。因此，不要求四个销的轴线垂直于扳手端面，也不要求四个销的几何图框的轴线与扳手外圆柱面或内孔的轴线同轴线。
• 孔组位置度公差带与各孔位置度公差带重合，几何图框轴线对基准轴线的允许变动量δl等于各孔位置度公差值t1 与该孔直径的尺寸公差值T 之和。
• δl=t1+T
• 满足第二种设计要求：（图6-10）

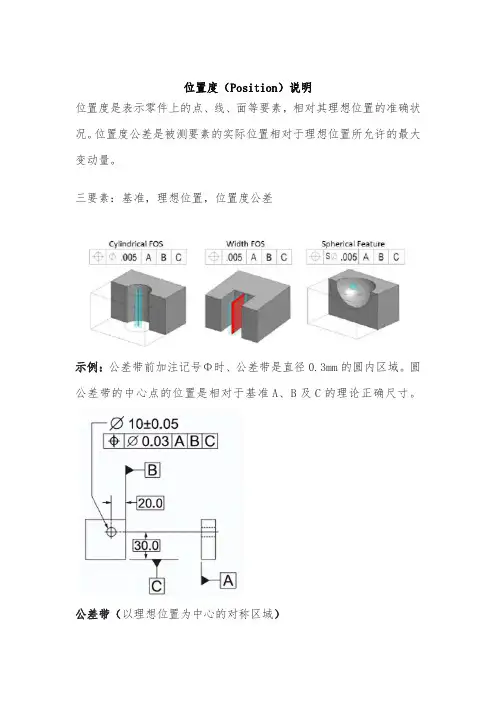
位置度(Position)说明

位置度（Position）说明位置度是表示零件上的点、线、面等要素，相对其理想位置的准确状况。

位置度公差是被测要素的实际位置相对于理想位置所允许的最大变动量。

三要素：基准，理想位置，位置度公差示例：公差带前加注记号Φ时、公差带是直径0.3mm的圆内区域。

圆公差带的中心点的位置是相对于基准A、B及C的理论正确尺寸。

公差带（以理想位置为中心的对称区域）公差带计算1.点的位置度公差如公差值前加注Φ，公差带是直径为公差值t的圆内的区域。

圆公差带的中心点的位置由相对于基准A和B的理论正确尺寸确定。

两个中心线的交点必须位于直径为公差值0.3的圆内，该圆的圆心位于由相对基准A和B(基准直线)的理论正确尺寸所确定的点的理想位置上。

如公差值前加注SΦ，公差带是直径为公差值t的球内的区域。

球公差带的中心点的位置由相对于基准A、B、和C的理论正确尺寸确定。

被测球的球心必须位于直径为公差值的0.3的球内。

该球的球心位于由相对基准A、B、C的理论正确尺寸所确定的理想位置上。

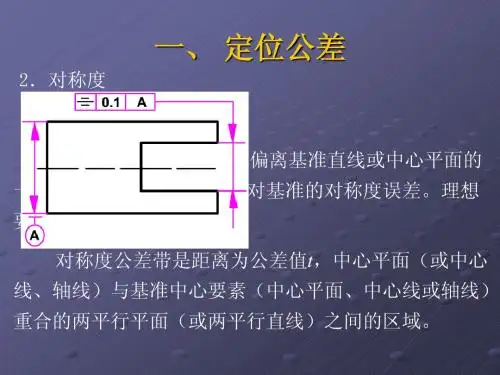
2.线位置度公差公差带是距离为公差值t且以线的理想位置为中心线对称配置的两平行直线之间的区域。

中心线的位置由相对于基准A的理论正确尺寸确定，此位置度公差仅给定一个方向。

每根刻线的中心线必须位于距离为公差值0.05且由相对于基准A的理论正确尺寸所确定的理想位置对称的诸两平行直线之间。

公差带是两对互相垂直的距离为t1和t2且以轴线的理想位置为中心对称配置的两平行平面之间的区域。

轴线的理想位置是由相对于三基面体系的理论正确尺寸确定的，此位置度公差相对于基准给定互相垂直的两个方向。

各个被测孔的轴线必须分别位于两对互相垂直的距离为公差值0.05和0.2，由相对于C、A、B基准表面(基准平面)理论正确尺寸所确定的理想位置对称配置的两平行平面之间。

如在公差值前加注Φ，则公差带是直径为t的圆柱面内的区域。

公差带的轴线的位置由相对于三基面体系的理论正确尺寸确定。

被测轴线必须位于直径为公差值Φ0.08且以相对于C、A、B基准表面(基准平面)的理论正确尺寸所确定的理想位置为轴线的圆柱面内。

位置度计算.

二板件各4个光孔用4个M4螺栓连接（活动紧固件连接）
ØT 0.5 M M Ø
图 9
若上例中光孔尺寸为 Ø 4 B11 求：T1、T2 ？
+ 0.215 + 0.140
[ MMS（H）= 4 .14 ]
计算： A）由式 (2)：H = F +（T1+T2）/2 4.14 = 4 +（T1+T2）/2 则： T1+ T2 = 0.28 ， T1 = T2 = 0.14 。 B）由式 (1)：T = H – F = 4.14 - 4 = 0.14。若上例中已知位置度公差都为Ø0.5 求：光孔H的MMS尺寸？计算： A）由式 (2)：H = F +（T1+T2）/2 = 4 +（0.51+ 0.5）/2 则： H = 4.5 。 B）由式 (1)：H = F + T = 4 + 0.5 = 4.5 。
图 6
4
B）“固定”紧固件连接
H
F
ØT
图 7
设： H – 光孔的MMS F – 紧固件(轴)的MMS T – 公差带大小 C min – 孔与轴的最小间隙则： F/2 = H/2 – T F = H – 2T T =（H – F）/2 = C min/2 …（5）
公式的讨论： T1 ≠ T2 ≠ T 则： F = H -（T1 +T2 ）
+ 0.12 0
件1
4 - Ø 3.5
0 - 0.12
件2
ØT1 M
ØT2 M
图 12
计算： A）由式 (6) 得： H = F + T1 + T2， 4 = 3.5 + T1+T2 则： T1+T2 = 0.5 如： T1 = T2 = 0.25 或 T1 = 0.2， T2 = 0.3 等。 B）由式 (5) 得：T =（H - F）/2 =（4 – 3.5）/2 = 0.25

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、位置度公差注法的原理
在几何精度设计中，确定中心距是一个重要的方面。
坐标尺寸注法存在着以下缺点： 1.加工时产生累积误差； 2.用两点法测量各个中心距不能保证坐标方向。位置度公差注法建立在由理论正确尺寸和几何图框给
出的理想位置上。见图6-1到6-5。
二、位置度公差的标注
单个要素在零件上的定位要求，可以根据基准体系和理论正确尺寸确定的理想位置标注位置度公差来实现。
δl=t1+T
满足第二种设计要求：（图6-10）
图6-10（a），各被测孔的轴线对
基准轴线的允许变动量：
δl=t1+T+T1 t1和T——被测孔的位置度公差值和
尺寸公差值；
T1——基准孔的尺寸公差值图6-10（b），各被测孔的轴线对
基准轴线的允许变动量：
δl=t1+T+T1+t3 t1和T——被测孔的位置度公差值和
三、位置度公差的计算
1. 孔组内各孔位置度公差的计算孔组内各孔的位置度公差带计算公式由紧固件与被连接零件
的连接方式决定。通孔连接方式：用螺栓、销钉等紧固件穿过两个或几个被连
接零件上的通孔；螺孔连接方式：把双头螺柱、螺钉等紧固件拧入一个被连接
零件的螺孔中，且穿过其余的被连接零件上的通孔。（1）通孔连接方式的位置度公差计算（图6-14）
公差值相同，而通孔的位置度公差采用最大实体要求，螺孔的位置度公差不采用最大实体要求，而采用独立原则。
t=（DM-dM）/2=0.5Xmin 上式中，紧固件采用包容要求
三、位置度公差的计算
2. 孔组位置度公差的计算（1）矩形零件（基准要素为平面要素）满足第一种设计要求：只需计算各孔位置度公差值t1，不必
孔组应平行于一个侧面的注法，见图6-9。
二、位置度公差的标注
（2）圆周布置孔组。 ①基准孔尺寸公差与被测孔位置度公差的关系采用最
大实体要求：图6-10。 ②不规定孔组在零件上的确定位置：图6-11、6-12。
图6-11所示的爪形扳手上的四销组内四个销只要求能够分别插入螺纹堵盖上的四孔组内四个孔中，可以施力，但不要求它们的端面贴合。因此，不要求四个销的轴线垂直于扳手端面，也不要求四个销的几何图框的轴线与扳手外圆柱面或内孔的轴线同轴线。
计算孔组位置度公差值t2，因为它们相等。（图6-6）
满足第二种设计要求：（图6-7和图6-4）
t2=δl-T δl为孔的轴线至零件有关侧面的距离的允许变动量，T为通孔直径的尺寸公差值
定位尺寸公差值：T 1=T2=δl
（2）圆盘形零件（基准要素为轴线）
满足第一种设计要求：（图6-5）
孔组位置度公差带与各孔位置度公差带重合，几何图框轴线对基准轴线的允许变动量δl等于各孔位置度公差值t1 与该孔直径的尺寸ห้องสมุดไป่ตู้差值T 之和。
t2 = δl –T-T1 T——被测孔的尺寸公差值
T1——基准孔的尺寸公差值
四、位置度公差标准数值的选择方法
1. 按GB/T 1184-1996选择位置度公差标准数值
二、位置度公差的标注
2.孔组位置度公差的基本标注方法满足第一种设计要求的位置度公差注法（1）矩形布置孔组。图6-6。
二、位置度公差的标注
（2）圆周布置孔组。图6-5。
二、位置度公差的标注
2.孔组位置度公差的基本标注方法满足第二种设计要求的位置度公差注法（1）矩形布置孔组。 ①复合位置度公差注法：指将孔组的两种位置度公差
要素组在零件上的定位，要考虑该要素组的两种位置关系和两种设计要求。
1.孔组位置度公差标注应包含的两项主要内容孔组的两种位置关系（1）孔组内各孔的位置关系。是指几何图框上各孔理想位
置之间的关系，各孔之间保持定的坐标位置关系和几何关系。（各孔位置度公差）（2）孔组对零件上其他要素的位置关系。是指孔组或孔组内各孔在零件上的定位要求。（孔组位置度公差）
分别用两个公差框格注出。图6-7。
孔组位置度公差各孔位置度公差
二、位置度公差的标注
②位置度公差与定位尺寸公差组合注法：图6-4和6-8。
四个孔的实际轴线必须位于Φt1位置度公差带内，且I、II、III孔的实际轴线还必须位于相应的定位尺寸公差带内，才能满足设计要求。
二、位置度公差的标注
二、位置度公差的标注
孔组的两种设计要求（1）第一种设计要求。装配时不仅要求被连接的两个零件
上对应孔组内各孔的位置分别对准，而且要求这两个零件上的某些其他要素也应分别对准。（对孔组和各孔的位置变动量都应规定较严格的位置度公差。）（2）第二种设计要求。装配时仅要求被连接的两个零件上对应孔组内各孔的位置分别对准，而不要求这两个零件上的某些其他要素也分别对准。（对各孔的位置变动量应规定较严格的位置度公差，而对孔组位置度公差或定位尺寸公差则应规定的较松。）孔组位置度公差与各孔位置度公差的关系：前者一定要不小于后者。
图6-12所示的滤油网盖上四孔组内四个孔的轴线应垂直于基准端面A，因为装配时该端面与箱体上相应的端面贴合。但不要求四个孔的几何图框的轴线与滤油网盖外圆柱面或内孔的轴线重合。
③复合位置度公差注法：图6-13。
四个孔的实际轴线应同时位于孔组位置度公差带和各孔位置度公差带内，即四个孔的实际轴线应位于两个公差带的重叠部分，但各孔位置度公差带中心不必位于孔组位置度公差带内，则满足设计要求。
尺寸公差值；
T1和t3——基准孔的尺寸公差值和垂直度公差值
三、位置度公差的计算
装配时，如果设计要求各个被连接零件上孔组内各孔分别对准，但不要求这些零件的外圆柱面或内孔的基准轴线彼此重合，则可采用图6-11、图6-12或6-13所示注法。
δl=t1+T+tp Tp——销组或孔组几何图框轴线对外圆柱面或内孔轴线的一般同轴度公差值
t=DM-dM=Xmin 上式中，紧固件采用包容要求
一般情况，各零件上通孔直径的基本尺寸和极限偏差都相同，其轴线的位置度公差值也相同，且采用最大实体要求，通孔的形状误差由最大实体实效边界控制。
三、位置度公差的计算
（2）螺孔连接方式的位置度公差计算（图6-15）一般情况下，螺孔（包括过盈配合销钉孔）和通孔的位置度