由一道课本习题出发

一年级数学书页问题练习题1. 问题描述在一年级的数学课本上，有一道与页码有关的问题练习题。

问题如下："某一年级数学书的页码是从1开始的。

这本书总共有60页。

请问这本书的页码中包含了多少个数字1？"请你解答这个问题，并列出具体的计算步骤和答案。

2. 解答步骤为了解答这个问题，我们可以按照以下步骤进行计算：Step 1: 在第一页，我们可以发现1这个数字出现了1次。

Step 2: 接下来，在第10页到19页之间，数字1又出现了10次（11, 12, 13, ..., 19）。

Step 3: 在第20页到29页之间，数字1仅出现了1次（21）。

Step 4: 继续计算，在第30页到39页之间，数字1不再出现。

Step 5: 在第40页到49页之间，数字1又出现了10次（41, 42, 43, ..., 49）。

Step 6: 最后，在第50页到60页之间，数字1又出现了11次（51, 52, 53, ..., 59, 60）。

3. 计算结果根据上述步骤，我们可以将数字1出现的次数相加：1 + 10 + 1 + 0 + 10 + 11 = 33因此，这本一年级数学书的页码中包含了33个数字1。

4. 总结通过本次练习题，我们学习了如何计算一本书中页码中特定数字的出现次数。

在本例中，我们计算了一年级数学书中数字1出现的次数为33次。

这种类型的问题可以帮助学生加深对数字的理解，同时提高计算能力和逻辑思维能力。

通过解决这类练习题，学生可以巩固对数字的认知，并培养解决问题的能力。

因此，数学课本中的问题练习题在帮助学生提高数学水平方面起到重要的作用。

总之，这道题目要求我们计算一年级数学书页码中数字1的出现次数，并通过具体步骤进行解答。

通过对这个问题的解答，我们能够提高学生的计算技巧和逻辑思维能力，培养他们解决问题的能力。

极化恒等式在向量数量积中的运用——由苏教版必修四的一道课后习题引发的思考周俊【摘要】极化恒等式是泛函分析中联系内积与范数的公式,即(x,y)=1/4(||x+y||2+||x-y||2),由于范数本身就是有关矢量的函数,因此泛函数分析中的极化恒等式就可以迁移到高中平面向量中,得到高中阶段学生可理解的极化恒等式,即a·b=1/4[(a+b)2-(a-b)2].利用这种极化恒等式可以解决向量的数量积.【期刊名称】《数学教学通讯：中教版》【年(卷),期】2017(000)009【总页数】2页(P42-43)【关键词】极化恒等式;向量数量积【作者】周俊【作者单位】江苏省宜兴市第二高级中学 214200【正文语种】中文周俊江苏省宜兴市第二高级中学214200最初引发笔者极化恒等式思考的是苏教版必修4平面向量数量积的一道课相加即可．从几何角度来解释这一公式，即：平行四边形对角线的平方和等于四条边的平方和．反思这一解决过程，可以发现这一公式解释了平行四边形对角线长度与四边长度的数量关系，但若将①式和②式相减时，可得到4a·b=（a+ b）2－（a－b）2，从几何角度来解释，即平行四边形共起点的邻边向量的数量积等于四分之一的两向量和的平方与两向量差的平方之差．换句话说，这一公式解决了平行四边形中共起点的向量数量积与两对角线之间的数量关系．为了验证这一结论的可用性，笔者在互联网上寻找与之间相似的结论与题目，百度百科跳出的一个叫极化恒等式的页面，让笔者对于这一结论有了更清晰的认知．极化恒等式是泛函分析中联在本质上就是一个关于向量的表达式．从而泛函数分析中的极化恒等式就可以迁移到高中平面向量中，得到高中阶段学生可理解的极化恒等式，b）2－（a－b）2］．极化恒等式的几何模型如图1所示，继续深入思考这个问题，可以提出这样的疑问：难道极化恒等式一定只有在平行四边形的问题情境中才能运用吗？答案显然是否定的，由于平行四边形法则与三角形法则是一致的，所以如果出现如图2所示三角形的几何模型时也可以用极化恒等式，可将三角形补全成平行四边形即可．这就为我们解决共起点的向量数量积提供了契机，取BC中此就可将极化恒等式由最初的平行四边形的几何模型，推广到更一般的具有共起点特性的几何模型上．透过上述两个几何模型，可以想象要利用极化恒等式解决向量数量积的问题，有一个必要的条件，即：两向量必须共起点．当满足共起点的前提后，就可连接起点与两向量差向量的中点来构造极化恒等式．极化恒等式能够巧妙地解决向量数量积的问题，因此，是高考命题的热点问题．这一点在江苏和浙江两大高考大省在高考命题和调研命题中对于其偏爱可见一斑．江苏省2014年高考填空第12题和2016年高考填空第13题，浙江省2012年填空题、湖州市2015年二模试卷均是极化恒等式解决向量数量积的题目．文章以江苏省2014年高考第12题和湖州市二模调研卷的两道真题作为剖析极化恒等式的例题．例1（江苏2014年高考第12题）如图3，在平行四边形ABCD中，已知AB=8，值为__________．反思：这是极化恒等式的逆向使用，由两个向量的数量积等于0，以极化恒等式为桥梁构造两个向量的和向量与差向量的模的数量关系．极化恒等式作为联系向量数量积与和差向量的桥梁而存在，其几何意义是共起点的向量数量积的四倍等于两向量和的平方与差的平方作差．从数量积的定义表达式来看两向量的数量积是关涉几何长度和角度的问题；而经过极化恒等式处理后，向量数量积则仅仅是关涉几何长度的问题．因此，从解决问题需要考虑的数学量的种类而言，利用极化恒等式可以缩减需要考虑几何量的种类，从而在一定程度上减少思维和计算的复杂程度．在利用极化恒等式时需要考虑向量共起点这一前提，当然这并不是说问题情境中待求数量积不共起点就不能使用极化恒等式，从向量共线的角度看，任意两个向量均可通过共线向量的平移而达到共起点的目的．因此，若待求数量积是在非共线的情况下，就需要一个过渡，将待求向量数量积进行一定程度的转化，使之成为共起点的向量数量积．另外需要注意的是极化恒等式的利用并不是直来直往的，有时需要学生在利用的过程中，像处理2014年江苏高考题一样去构造辅助点；有时需要学生像解2015年湖州二模题一样，在已知两向量数量积的情况下，将极化恒等式逆向使用，求解和差向量的数量关系．而对于极化恒等式的教学一般建议在新授必修课时不要直接讲授，因为向量数量积毕竟是一种技巧性的解题方法，技巧的掌握是需要一定的知识基础的．而且教学之道在根本上应当是教授知识的本质，在向量数量积的教学中数量积的定义求解才是数量积的本质，新授课若直接讲解极化恒等式有一种舍本逐末的教学倾向，极易造成学生忽视数量积的基础知识．因此，关于极化恒等式的教学应当注意在平时教学中的逐步渗透，让学生在打好数量的基础后再进行极化恒等式的教学．。

人教版五年级下册数学课本习题归类长方体和正方体局部1、工人叔叔要在工人俱乐部的四周装上彩灯〔地面的四周不装〕，工人俱乐部的长是90m，宽是55m，高是20m，至少需要多长的彩灯线？2、小卖部要做一个长2.2m，宽44cm，高80cm的玻璃柜台，现要在柜台各边都安上角铁，这个柜台需要多少米角铁？3、亮亮家要给一个长0.75m，宽0.5m，高1.6m的简易衣柜换布罩，至少需要用布多少平方米？4、一个玻璃鱼缸的形状是正方形，棱长3dm，制作这个鱼缸至少需要玻璃多少平方分米？5、光华街口装了一个新的铁皮邮筒，长50cm，宽40cm，高78cm。

做这个邮箱至少需要多少平方厘米的铁皮？6、把一个棱长46 cm的正方形纸箱的各面都贴上红纸，至少需要多少平方厘米的红纸？7、一个长方体的饼干箱，长10cm，宽6cm，高12cm，如果围着它贴一圈商标纸〔上下面不贴〕，这行商标纸的面积至少是多少平方厘米？8、加工一批洗衣机的机罩〔没有底面〕，每台洗衣机的长59.5cm，宽42.5cm，高80cm，做1000个机套至少用布多少平方米？9、一根长方体木料，长5m，横截面的面积是0.06㎡，这跟木料的体积是多少？10、建筑工地要挖一个长50m，宽30m，深50m的长方体土坑，挖出多少方的土？11、一块棱长30cm的正方体冰块，它的体积是多少?12、奶奶的生日蛋糕长2dm，宽2dm，高0.6dm，奶奶把他平均分成4块长方体形状的小蛋糕，想一想她是怎样分的，每个人分到多大的一块蛋糕？13、家具厂订购500根方木，每根方木横截面的面积是24 d㎡，长3m。

这些木料一共是多少方?14、一个包装盒，如果从里面量长28cm，宽20cm，体积为11.76 d㎡。

爸爸想用它包装一件长25cm，宽16cm，高8cm的玻璃器皿，是否可以装下？15、用棱长3cm的正方体在广场中央搭了一面长6m，宽2.7m，厚6cm的奥运心愿墙，算一算这面墙共用了多少块积木？16、公园南面要修建一道长15m，厚24cm，高3m的围墙。

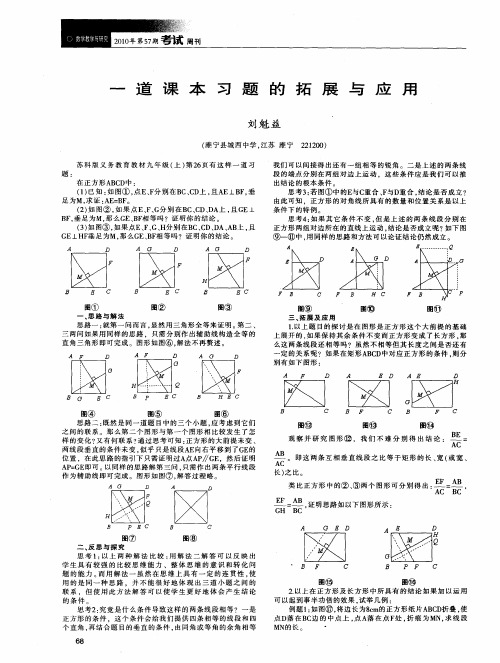
一道课本习题的多种变式一道课本习题原题再现：如图，在△ABC中，∠ABC=80°，∠ACB=50°，BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.【简析】：本题是学生在学完三角形的内角和以及外角性质之后，课本出现的一道习题。

我们通过角平分线的性质可求得：∠PBC=40°，∠PCB=25°，从而根据三角形内角和定理，求出∠BPC=115°.下面就是这道课本习题的多种变式：【变式1】：如图1,在△ABC中，BP平分∠ABC,CP平分∠ACB,求∠BPC与∠A的数量关系。

小结：本题通过三角形的内角和定理以及外角性质探究两条内角的平分线所夹的角与三角形第三个角的关系。

【变式2】如图5,在△ABC中，BP平分∠ABC,CP平分∠ACB的外角∠ACD,求∠P与∠A的数量关系。

【思考】：一条内角平分线和一条外角平分线，他们的数量关系又是怎么样的呢？不仿先通过量角器大胆发现，果然，我们发现他们存在倍数关系，即：∠P=0.5∠A.借助三角形的外角性质，本题不难证明。

（当然也可以利用三角形的内角和等于180°进行证明）【简析】：如图5，因为BP平分∠ABC,CP平分∠ACD所以：∠ACD=2∠4，∠ABC=2∠1由外角性质得：∠P=∠4-∠1所以：∠A=∠ACD-∠ABC=2∠4-2∠1=2（∠4-∠1）=2∠P即：∠P=0.5∠A.小结：当三角形的一条内角平分线和外角平分线有交点时，我们不难发现第三个角和这个夹角存在倍数关系。

【变式3】如图6,在△ABC中，BP，CP分别平分∠ABC和∠ACB的外角,求∠P与∠A的数量关系.【思考】:三角形的两条外角平分线所夹的角和∠A又有何关系呢，会不会和上面两题的结论有什么联系？我们发现：∠P=90°-0.5∠A.具体方法同学们可以模仿变式1的3种证明方法，这里不再具体证明。

总之，在一个三角形中，两条角平分线所夹的角，与三角形的第三个角之间隐藏的关系，我们探索到这里，希望同学们能够做到一题多变，一题多解，发散自己的思维，这样就能举一反三，快乐地遨游在数学的海洋里.。

部编⼈教版四年级语⽂上册课本课后习题（参考答案）部编版四年级语⽂上册课本课后习题参考答案第⼀课《观潮》⼀、说说课⽂是按照什么顺序描写钱塘江⼤潮的，你的头脑中浮现出怎样的画⾯，选择印象最深和同学交流。

答：课⽂按潮来前，潮来时，潮过后的顺序观察描写钱塘江⼤潮。

“潮来前”的景象：江⾯上很平静，观潮⼈的⼼情急切。

闷雷滚动、⼀条⽩线“潮来时”的景象：潮的声⼤，潮头有数丈之⾼，声如“⼭崩地裂”，形如“⽩⾊城墙”、“⽩⾊战马”，横贯江⾯。

给⼈的印象就是如巨雷般的⼤潮像千军万马席地⽽卷，在呐喊、嘶鸣中奔来。

狂潮拍⽯，如同⼏⾥岸边同时⾦钟齐鸣。

“潮头过后”的景象：潮头汹涌，漫天卷地，余威犹在，恢复平静，⽔位上涨。

我印象最深的是“潮来时”的景象：那条⽩线很快地向我们移来，逐渐拉长，变粗，横贯江⾯。

再近些，只见⽩浪翻滚，形成⼀堵两丈多⾼的⽔墙。

浪潮越来越近，犹如千万匹⽩⾊战马齐头并进，浩浩荡荡地飞奔⽽来；那声⾳如同⼭崩地裂，好像⼤地都被震得颤动起来。

霎时，潮头奔腾西去，可是余波还在漫天卷地般涌来，江⾯上依旧风号浪吼。

⼆、读下⾯这⾸诗，从课⽂中找出与诗的内容相关的句⼦。

浪淘沙唐·刘禹锡⼋⽉涛声吼地来，头⾼数丈触⼭回。

须臾却⼊海门去，卷起沙堆似雪堆。

与诗的内容相关的句⼦：那条⽩线很快地向我们移来，逐渐拉长，变粗，横贯江⾯。

再近些，只见⽩浪翻滚，形成⼀堵两丈多⾼的⽔墙。

浪潮越来越近，犹如千万匹⽩⾊战马齐头并进，浩浩荡荡地飞奔⽽来；那声⾳如同⼭崩地裂，好像⼤地都被震得颤动起来。

第⼆课《⾛⽉亮》⼀、阿妈牵着我“我”⾛过“⽉光闪闪的溪岸”，“细细的溪⽔，流着⼭草和野花的⾹味，流着⽉光……”你的头脑中浮出了怎样的画⾯？课⽂中还有哪些画⾯给你留下了深刻的印象？和同学交流。

提⽰：⼭草、野花、⽉光倒映在溪⽔⾥，随着溪⽔流动着，就像是“流着⼭草、野花的⾹味，流着⽉光”。

这⾥⽤了暗喻的⼿法，把阿妈⽐作美丽的⽉亮，牵着那些闪闪烁烁的⼩星星，也就是“我”在天上⾛着。