圆内接正五边形画法

尺规正五边形的画法
正五边形是一个边长相等、五个内角均为108 度的多边形。

尺规法是一种使用直尺和圆规的传统构图方法，用于构图复杂的几何图形，包括正五边形。

下面是具体的尺规画正五边形的步骤：
1. 画一条横线作为正五边形的底边，将底边的中心点记为O。

2. 以O 为圆心，任选一个合适的半径，画一个圆。

3. 以圆上一个点为端点，再以圆心为端点，画一条线段，将圆分成两个部分。

4. 以圆上与底边相交的两个点为端点，再以底边为端点，分别画两条线段，得到两个等边三角形。

5. 以其中一个等边三角形的顶点为圆心，以这个三角形边长为半径，画一个圆。

6. 以圆上与底边相交的一个点为端点，再以圆心为端点，画一条线段。

7. 以圆心为顶点，分别以这两条线段为边长，画两个等边三角形。

8. 在这两个等边三角形的公共边上，再次以这个边为底边，画两个等边三角形。

9. 重复执行步骤5-8，最终就可以得到一个完整的正五边形。

需要注意的是，在使用尺规画正五边形时，需要准确操作圆规并精确测量线段的长度，画图过程中需要耐心、细心地逐步推导，才能得到准确的结果。

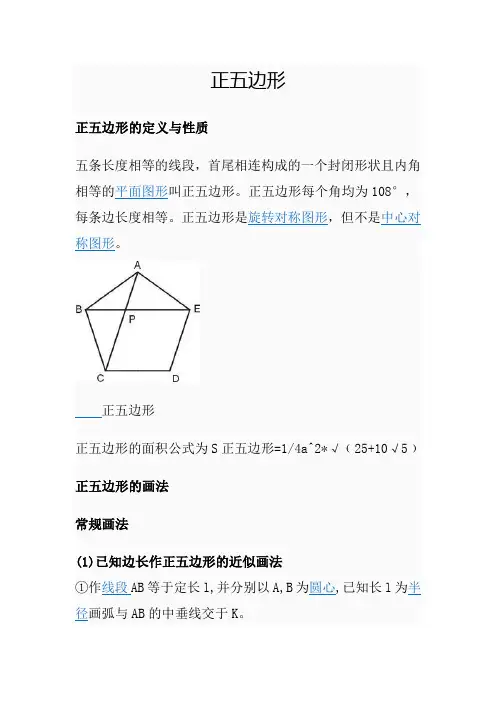
②取AB的2/3长度延长AK到C，使CK=2/3AB。

③以点C为圆心，已知边长AB为半径画弧，分别与前两弧相交于M，N。

④顺次连接A，B，N，C，M各点即近似作得所要求的正五边形。

(2)民间口诀画正五边形口诀介绍：“九五顶五九,八五两边分”。

画法:①画线段AB=20mm。

②作线段AB的垂直平分线l，垂足为G。

③在l上连续截取GH，HD，使 GH=9.5/5*10mm=19mm，HD=5.9/5*10mm=11.8mm。

④过H作EC⊥HG,在EC上截取HE=HC=8/5*10mm=16mm。

⑤连结DE，EA，AB，BC，CD。

五边形ABCDE就是边长为20mm的近似正五边形。

尺规作图画法理论依据：cos36°=(1+√5)/4正五边形 - 几何画板1. 在平面内作一圆，圆心为O；2. 在圆O上取一点A，连接AO并延长交圆O于另一点B；【假令|AB|=4】3. 过点O作CD⊥AB，交圆O于C、D两点；【此时|CD|=4】4. 作OB垂直平分线MN，交OB于E点，交圆O于M，N【此时|OE|=|BE|=2】5. 以点E为圆心，EC长为半径作弧，交BO延长线于点F；【此时|EC|=|EF|=√5】6. 以点B为圆心，BF长为半径作弧，交圆O分别于G、H两点；【此时|BF|=|EF|+|BE|=1+√5】【此时可知cos∠ABG=(|EF|+|BE|)/|AB|=(1+√5)/4=36°】【而∠AOG=2∠ABG=72°=360°/5(直径所对的圆周角)】【此时便得到了圆周上的五等分点的其中两个。

】7. 以点G为圆心，GA长为半径作弧，交圆O于P点；8. 以点H为圆心，HA长为半径作弧，交圆O于Q点；9. 连接AG、GP、PQ、QH、HA,则五边形AGPQH为正五边形。

圆内接正五边形圆内接正五边形的定义与性质圆内接正五边形指内接于圆的正五边形。

圆内接正五边形的每一条边相等（即圆的每一条弦相等），每个角均为108°，每个角在圆内所对的优弧相等。

圆五等分最简单的方法
圆的五等分画法
1、设该圆中心为O点，做圆O直径AB；
2、在此圆中再作一直径CD，使CD垂直于AB；
3、以半径OA的中点M为圆心，以MC为半径作弧交线段AB于点N；
4、连结NC。

则线段NC即该圆的内接正五边形边长。

5、做出正五边形，由等边对等弧即可将圆五等分了。

圆是一种几何图形，指的是平面中到一个定点距离为定值的所有点的集合。

这个给定的点称为圆的圆心。

作为定值的距离称为圆的半径。

当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹就是一个圆。

圆的直径有无数条；圆的对称轴有无数条。

圆的直径是半径的2倍，圆的半径是直径的一半。

用圆规画圆时，针尖所在的点叫做圆心，一般用字母O表示。

连接圆心和圆上任意一点的线段叫做半径，一般用字母r表示，半径的长度就是圆规两个角之间的距离。

通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。

圆是平面上的曲线图形，是一个轴对称图形，它的对称轴是直径所在的直线，圆有无数条对称轴。

请用尺规作图法画出一个正五边形。

请用尺规作图法画出一个正五边形
正五边形是一个有五条相等边和五个相等角的多边形。

尺规作图法是根据几何构造的原理，使用尺子（直尺）和圆规来绘制几何图形。

以下是使用尺规作图法绘制正五边形的步骤：
1. 先画一个任意圆。

假设圆心为O，半径为r。

2. 在圆上选择一个点A，并将尺子的一边放在A上，另一边延长到圆上的另一点B，使得AB的长度等于圆的半径r。

3. 以点A为圆心，以AB的长度为半径，作一条弧线，与圆交于点C。

4. 将尺子的一边放在点A上，另一边延长到点C，再将尺子放在点C上，另一边延长到圆上的另一点D。

5. 以点C为圆心，以CD的长度为半径，作一条弧线，与圆交于点E。

6. 连接OA、OC、OE，得到一个正五边形。

注意事项：
- 在绘制过程中，尽量保持尺子的边与圆的周边平行，这样可以保证绘制出的正五边形更精确。

- 在选择点B和点D时，确保它们与圆弧的切点即可。

尺规作图法是根据严格的几何构造规则进行的，在实际操作中可能需要一些技巧和练习才能画出完美的正五边形。

希望以上步骤对您有所帮助。

祝您绘制成功！。

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆，设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心，MA为半径作圆，交OX于点N；5、以点A为圆心，AN为半径，在圆上连续截取等弧，使弦AB=BC=CD=DE=AN，则五边形ABCDE即为正五边形。

以上两种图形的作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的直规作图方法．确实，有的困难一些，有的容易一些．正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi （i为右下角标）＝22i（底数2指数2的i次幂）＋1 的数．费马的一个著名猜想是，当n≥3时，不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数，对于i＝0，1，2，3，4时，容易算出来相应的Fi：F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k（2的k次幂）或2k×p1×p2×…×ps，（1，2…s为右下角标）其中，p1，p2，…，ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正 13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而 3=F0．。

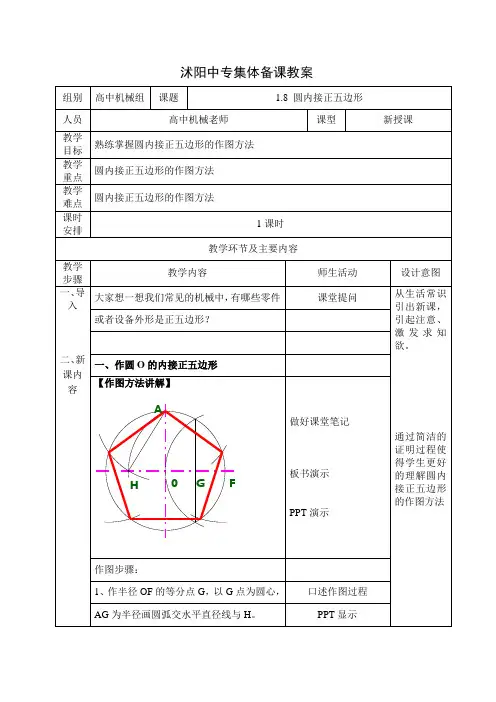
尺规作图的简介尺规作图是指用没有刻度的直尺和圆规作图。

一把没有刻度的直尺看似不能做什么，画一个圆又不知道它的半径，画线段又没有精确的长度。

其实尺规作图的用处很大，比如单用圆规找出一个圆的圆心，量度一个角的角度，等等。

运用尺规作图可以画出与某个角相等的角，十分方便。

尺规作图是起源于古希腊的数学课题。

只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题。

平面几何作图，限制只能用直尺、圆规。

在历史上最先明确提出尺规限制的是伊诺皮迪斯。

他发现以下作图法：在已知直线的已知点上作一角与已知角相等。

这件事的重要性并不在于这个角的实际作出，而是在尺规的限制下从理论上去解决这个问题。

在这以前，许多作图题是不限工具的。

伊诺皮迪斯以后，尺规的限制逐渐成为一种公约,最后总结在《几何原本》之中。

若干著名的尺规作图已知是不可能的，而当中很多不可能证明是利用了由19世纪出现的伽罗华理论。

尽管如此，仍有很多业余爱好者尝试这些不可能的题目，当中以化圆为方及三等分任意角最受注意。

数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书。

■尺规作图的基本要求·它使用的直尺和圆规带有想像性质，跟现实中的并非完全相同：·直尺必须没有刻度，无限长，且只能使用直尺的固定一侧。

只可以用它来将两个点连在一起，不可以在上画刻度。

·圆规可以开至无限宽，但上面亦不能有刻度。

它只可以拉开成你之前构造过的长度。

■五种基本作图·作一个角等于已知角·平分已知角·作已知直线的垂直平分线·作一条线段等于已知线段·过一点作已知直线的垂线■尺规作图公法以下是尺规作图中可用的基本方法，也称为作图公法，任何尺规作图的步骤均可分解为以下五种方法：·通过两个已知点可作一直线。

·已知圆心和半径可作一个圆。

·若两已知直线相交，可求其交点。

圆内接正五边形原理
哎呀呀，说起圆内接正五边形原理，这可真是个有趣又有点难搞的东西呢！
你们知道吗？圆就像是一个大大的怀抱，能把正五边形紧紧地搂在怀里。

那正五边形是怎么在圆里舒舒服服待着的呢？这就得好好研究研究啦！
咱们先画一个圆，这圆啊，就像一个大舞台。

然后呢，要把这个舞台分成五等份，就好像要把一块大蛋糕平均切成五块一样。

这可不容易哟！
我们来算一算，圆的一圈是360 度，分成五等份，那一份不就是360÷5 = 72 度嘛！
这时候，咱们从圆心出发，向圆上画五条线，每条线之间的夹角就是72 度。

这五条线就像是五个大力士，把正五边形稳稳地撑在圆里面。

你们想想看，这五条线是不是很神奇？就像五个好朋友，手拉手，谁也不松开，共同守护着正五边形。

再仔细瞧瞧，这正五边形的五条边是不是长度都相等呀？这就好像五个兄弟姐妹，长得一模一样高，多整齐呀！
老师给我们讲这个的时候，我一开始还不太懂呢，心里想：“这咋这么复杂呀？”后来经过反复琢磨，才慢慢明白了其中的道理。

我还和同桌讨论来着，我问他：“你能一下子就明白这个原理不？”他摇摇头说：“哪有那么容易呀！”
咱们再想想，如果把正五边形换成正六边形、正七边形，那又会是怎样的情况呢？是不是会更复杂呢？
其实呀，圆内接正五边形原理在生活中也有不少用处呢！比如说建筑设计、美术画画，都能看到它的影子。

所以说，数学可真是神奇又有趣，只要咱们认真去研究，就能发现好多好多好玩的东西！这圆内接正五边形原理，不就是一个很好的例子吗？。

正五边形的画法原理
正五边形是一种具有五条相等边和五个相等角的多边形，它的构图方法有很多种，下面将介绍一种简单易懂的画法原理。

首先，我们需要准备一张白纸和一支铅笔。

在纸上画一个圆形，这个圆形将成
为正五边形的外接圆。

确定圆心后，用直尺在圆上画出水平线和垂直线，这两条线的交点就是正五边形的顶点之一。

接下来，我们需要确定正五边形的另外四个顶点。

在圆上选择一个点作为起始点，然后用直尺连接这个起始点和圆心，得到一条半径线。

然后，以这条半径线为边，将圆分成五等分，这样就确定了正五边形的五个顶点。

现在，我们可以开始画出正五边形的边了。

连接相邻的顶点，依次画出五条边，这样就完成了正五边形的画法。

需要注意的是，画出的五边形要保持边长相等，角度相等，才能称为正五边形。

在实际操作中，可以使用量角器和尺子来确保每条边的长度和每个角度的准确性。

除了使用外接圆的方法，还可以使用内切圆或者其他方法来画出正五边形。

无
论采用何种方法，都需要保证五边形的边长和角度的准确性，才能得到一个完美的正五边形。

总之，正五边形的画法原理并不复杂，只要掌握了正确的方法和技巧，就能够
轻松地画出一个完美的正五边形。

希望本文的介绍能够帮助到大家，让大家在绘画中更加游刃有余。