电工技术第二章 电路的分析方法习题解答

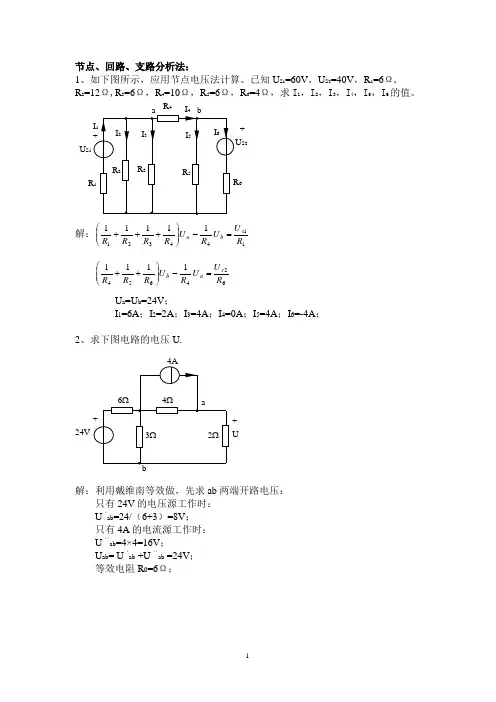
节点、回路、支路分析法：1、如下图所示，应用节点电压法计算。

已知U s 1=60V ，U s 2=40V ，R 1=6Ω,23456Ω，求I 1，I 2，I 3，I 4，I 5，I 6的值。

解：114432111111R U U R U R R R R s b a =-⎪⎪⎭⎫⎝⎛+++ 6246541111R U U R U R R R s a b =-⎪⎪⎭⎫ ⎝⎛++ U a =U b =24V ；I 1=6A ；I 2=2A ；I 3=4A ；I 4=0A ；I 5=4A ；I 6=-4A ；2、求下图电路的电压U.解：利用戴维南等效做，先求ab 两端开路电压：只有24V 的电压源工作时： U ‘ab =24/（6+3）=8V ； 只有4A 的电流源工作时： U ‘‘ab =4×4=16V ； U ab = U ‘ab +U ‘‘ab =24V ； 等效电阻R 0=6Ω；U= U ab /（6+2）×2=6V3、计算下图电路中的电压U 1与U 2.解：U 1=8×[4+(6//3)]/[18+4+(6//3)] ×18=36V; U 2=8×18/[18×4+(6//3)] ×3=12V .4、已知下图电路的回路方程为2I 1+I 2=4V 和4I 2=8V ，式中各电流的单位为安培。

求：（1） 各元件的参数；（2） 各电压源供出的功率；（3） 改变U s1和U s2的值，使各电阻的功率增加一倍。

解：（1）1+ R 3)I 1+R 3I 2+k U 1=Us 1 1+ R 3-k R 1)I 1+R 3I 2 =Us 1-k Us 1R 3I 1 + (R 2+ R 3)I 2+k U 1=Us 2U 1=Us 1- R 1I 1 3-k R 1) I 1+ (R 2+ R 3)I 2+k U 1=Us 2-k Us 1R 1=2Ω, R 2=3Ω, R 3=1Ω, Us 1=8V , Us 1=12V , k =0.5 （2）求解方程式，得到：I 1=1A, I 2=2A ，计算各电源功率：Us 1：P 1= Us 1 I 1=8W ； (发出) Us 2：P 2= Us 2 I 2=24W ； （发出） Ucs ：Pcs= Ucs (I 1+I 2)=9W ；（吸收） （3）各电源增加2倍，则各电阻上的电流相应增加2倍，即可实现目的。

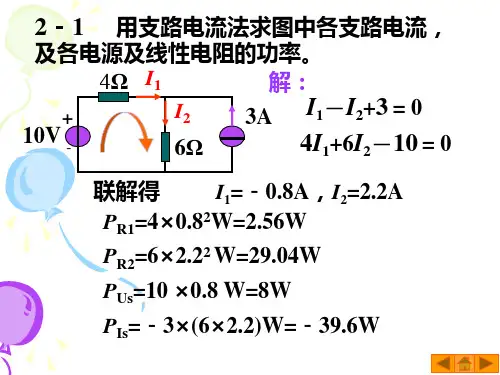
2.1.1 选择题（1）在图2-73所示电路中，发出功率的元件是__Ａ___。

（Ａ）仅是5Ｖ的电源（Ｂ）仅是2Ｖ的电源（Ｃ）仅是电流源（Ｄ）电压源和电流源都发出功率（Ｅ）条件不足图2-73题2.1.1（1）图图2-74题2.1.1（2）图（2）在图2-74所示电路中，当增大时，恒流源两端的电压Ｕ__B___。

（A）不变（B）升高（C）降低（3）在图2-75所示电路中，当开关S闭合后，P点的电位__B___。

（A）不变（B）升高（C）为零（4）在图2-76所示电路中，对负载电阻R而言，点画线框中的电路可用一个等效电源代替，该等效电源是__C___。

（A）理想电压源（B）理想电流源（C）不能确定图2-75题2.1.1（3）图图2-76题2.1.1（4）图(5) 实验测的某有源二端线性网络的开路电压为10V，当外接3Ω的电阻时，其端电压为6V，则该网络的戴维南等效电压的参数为(C)。

(a)U S=6V，R0=3Ω (b)U S=8V，R0=3Ω (c)U S=10V，R0=2Ω(6) 实验测得某有源二端线性网络的开路电压为6V，短路电流为3A。

当外接电阻为4Ω时，流过该电阻的电流I为( A )。

(a)1A(b)2A(c)3A(7) 在图2-77所示电路中，已知U S1=4V，U S2=4V，当U S2单独作用时，电阻R中的电流为1MA，那么当U S1单独作用时，电压U AB是（A）（A）1V （B）3V （C）-3V图2-77题2.1.1（7）图（8）一个具有几个结点，b条支路的电路，其独立的KVL方程为（B）a)（n-1）个 b)（b-n+1）个（9）一个具有几个结点，b条支路的电路，要确定全部支路电流，最少要测量（B）a)（n-1）次 b)（b-n+1）次（10）一个具有n个结点，b条支路的电路，要确定全部支路电压，最少要测量（A）a)（n-1）次 b)（b-n+1）次（11）电阻并联时，电阻值越大的电阻：（A）a)消耗功率越小； b)消耗功率越大。

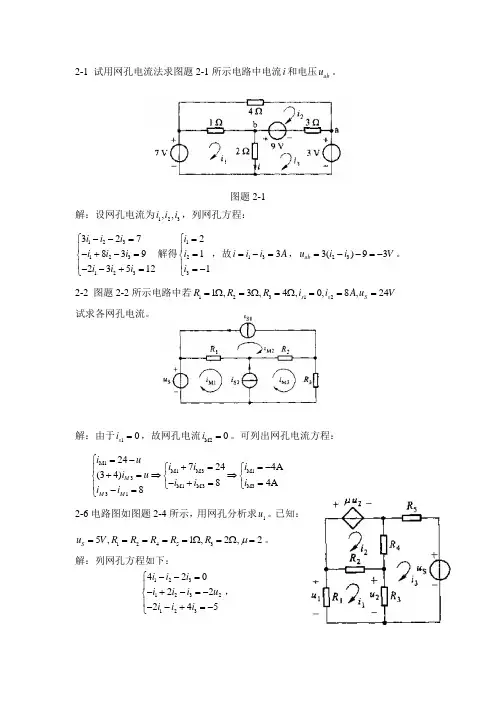
2-1 试用网孔电流法求图题2-1所示电路中电流i 和电压ab u 。

图题2-1解：设网孔电流为123,,i i i ，列网孔方程：12312312332783923512i i i i i i i i i --=⎧⎪-+-=⎨⎪--+=⎩解得123211i i i =⎧⎪=⎨⎪=-⎩，故133i i i A =-=，233()93ab u i i V =--=-。

2-2 图题2-2所示电路中若123121,3,4,0,8,24s s S R R R i i A u V =Ω=Ω=Ω=== 试求各网孔电流。

解：由于10s i =，故网孔电流M20i =。

可列出网孔电流方程：M1M1M3M13M3M1M331247244A (34)4A 88M M M i u i i i i u i i i i i =-⎧+==-⎧⎧⎪+=⇒⇒⎨⎨⎨=-+=⎩⎩⎪-=⎩ 2-6电路图如图题2-4所示，用网孔分析求1u 。

已知：124535,1,2,2S u V R R R R R μ=====Ω=Ω=。

解：列网孔方程如下：123123212342022245i i i i i i u i i i --=⎧⎪-+-=-⎨⎪--+=-⎩，再加上2132()u i i =-。

解得：11113.75, 3.75i A u R i V =-=-= 2-12 电路如图题2-10所示，试用节点分析求各支路电流。

解：标出节点编号，列出节点方程121111()27212211120()422227a a b a b b u V u u u u u V ⎧⎧=++-=⎪⎪⎪⎪⇒⎨⎨⎪⎪-++=-=⎪⎪⎩⎩，用欧姆定律即可求得各节点电流。

2-17电路如图题2-14所示，试用节点分析求12,i i 。

解：把受控电流源暂作为独立电流源，列出节点方程 12121(11)4(11)2u u u u i +-=⎧⎨-++=-⎩ 控制量与节点电压关系为：111u i =Ω，代入上式，解得 111222 1.61.610.80.81u i A u V u V u i A ⎧==⎪=⎧⎪Ω⇒⎨⎨=-⎩⎪==-⎪⎩Ω2-19 试列出为求解图题2-16所示电路中0u 所需的节点方程。

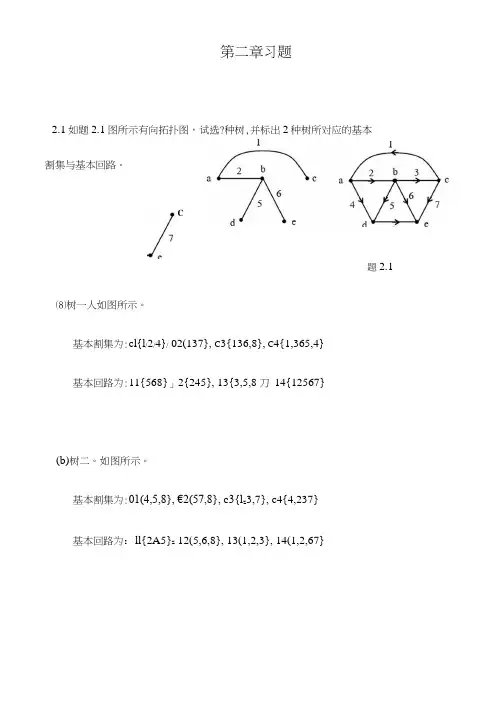
第二章习题2.1如题2.1图所示有向拓扑图，试选?种树,并标出2种树所对应的基本割集与基本回路。

C题2.1⑻树一人如图所示。

基本割集为:cl{l/2/4}/ 02(137}, C3{136,8}, C4{1,365,4}基本回路为:11{568}」2{245}, 13{3,5,8刀14{12567}(b)树二。

如图所示。

基本割集为:01(4,5,8}, €2(57,8}, c3{l z3,7}, c4{4,237}基本回路为：ll{2A5}z 12(5,6,8}, 13(1,2,3}, 14(1,2,67}解：列两个KVL 回路方程：4 厶+5(人+ 厶)+ 1 —5 = 0 10厶+5(人+ 厶)+ 1 — 2 = 0整理为：9人+ 5厶=45人+15人=1解彳昙：人=0.54 厶=—0.L4而/3 = —(/1 +12) = —0.4 A2.3如题2.3图所示电路，已知电流人=24 ,求电阻&解：可列KVL 回路方程:2I+2 + (i-3)R=3已知i=2A ，代入上式可得:R=3Q2.2题2.2图示电路,求支路电流人、 4Q10Q-3V42.4如题2.4图筛电路，试选-种树，确定基本回路，仅用孟本回路0.4110(i-6)+5(0.4i+i)+13i=0解得：i 二2A2.5如题2.5图所示电路，试选一种树■确定基本割集,仅用一个基本割集方程求解电压U.若用筋法，你将选择哪F 点作^ 6V12V i ■ ~O+TO+-3八5A+O 20Q [J U 8叩方程求解电流io解：23 Q ―I ZZF 6A5Q13Q程求电压U O解：①②选3为参考节点，列方程如下:（——+ —）U,-——心=一20 8 4 20 -已知心=-12U ,代入上式”有：1220 8 20解得节点点位：U4=-32V又可知“ +知+ 12 = 0 得: M =-M4-12=32-12=20V02 <T JCJ 寸 q^I n u- n uc{e -空M S F -由&扶・M !・.8d y l =(y +9)K H 2旅®眾皿・ si®隍画 9rxi§ 9.XIo II• •詁II s二CM II •匸II •J 3II ri• •T ii•r? +J + cc X ss J 1 CC II CC 7IIri1 en 1 II w =sII• • 呈tF • •-ffi• •®-ffiM l :丄(E +o +萃2.7如题2.7图所示平面电路，各网孔电流如图中所标,试列写出可用来求IQ 2Q 解该电路的网孔方程。

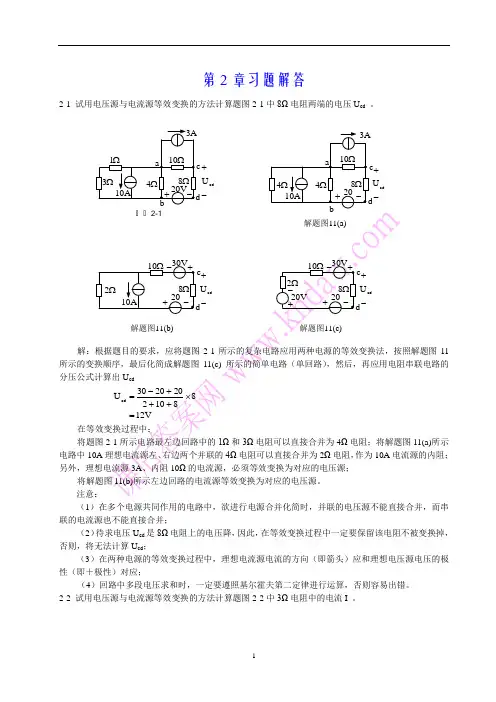
第2章习题解答2-1 试用电压源与电流源等效变换的方法计算题图2-1中8Ω电阻两端的电压U cd 。

解：根据题目的要求，应将题图2-111 将题图3Ω电阻可以直接合并为4Ω电阻；将解题图11(a)所示电路中10A 2Ω电阻，作为10A 电流源的内阻；注意：（1）在多个电源共同作用的电路中，欲进行电源合并化简时，并联的电压源不能直接合并，而串联的电流源也不能直接合并；（2）待求电压U cd 是8Ω电阻上的电压降，因此，在等效变换过程中一定要保留该电阻不被变换掉，否则，将无法计算U cd ；（3）在两种电源的等效变换过程中，理想电流源电流的方向（即箭头）应和理想电压源电压的极性（即＋极性）对应；（4）回路中多段电压求和时，一定要遵照基尔霍夫第二定律进行运算，否则容易出错。

2-2 试用电压源与电流源等效变换的方法计算题图2-2中3Ω电阻中的电流I 。

题题2-1 -+cd U-+cd U 解题图11(a)-+cdU 解题图11(b) -+cd题题2-2解题图12(a)解题图12(i)解题图12(j)解：根据题目的要求，应用两种电源的等效变换法，将题图2-2所示电路按照解题图12所示的变换顺序，最后化简为解题图12(j)所示的电路，电流I 为A 2.0822I =+=注意：(1) 一般情况下，与理想电流源串联的电阻可视为短路、而与理想电压源并联的电阻可视为开路。

故题图2-2所示电路最左边支路中的2Ω电阻可视为0；（2）在变换过程中，一定要保留待求电流I 的支路不被变换掉；（3）根据电路的结构，应按照a-b 、c-d 、e-f 的顺序化简，比较合理。

2-3 计算题图2-3中1Ω电阻上的电压U ab 。

V题题2-3Ω解题图13(b)ΩΩ解题图13(e)13的顺序化简，将题图2-3所示U ab 为2-4 试用电压源与电流源等效变换的方法计算题图2-4中2Ω电阻中的电流I 。

36题题2-4解题图14(a)解： A 122228I =++-=2-5 应用支路电流法计算题图2-5所示电路中的各支路电流。

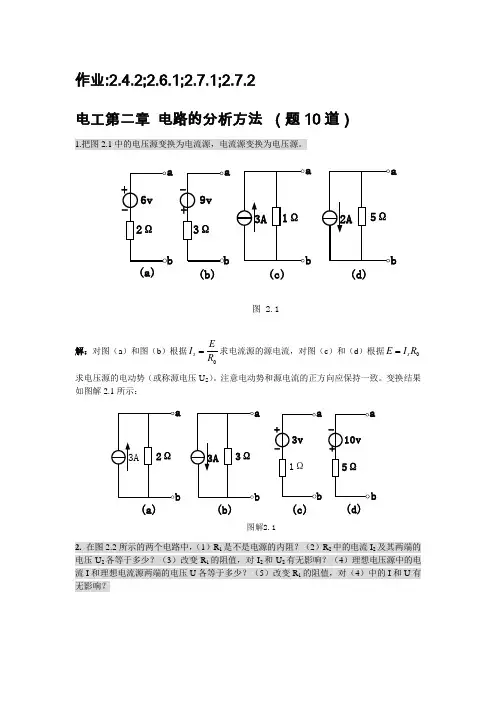
作业:2.4.2;2.6.1;2.7.1;2.7.2电工第二章电路的分析方法（题10道）1.把图2.1中的电压源变换为电流源，电流源变换为电压源。

(a)(b)(c)(d)图 2.1解：对图（a）和图（b）根据sEIR=求电流源的源电流，对图（c）和（d）根据sE I R=求电压源的电动势（或称源电压U S）。

注意电动势和源电流的正方向应保持一致。

变换结果如图解2.1所示：(c)(d)(a)(b)图解2.12. 在图2.2所示的两个电路中，（1）R1是不是电源的内阻？（2）R2中的电流I2及其两端的电压U2各等于多少？（3）改变R1的阻值，对I2和U2有无影响？（4）理想电压源中的电流I和理想电流源两端的电压U各等于多少？（5）改变R1的阻值，对（4）中的I和U有无影响？12VI 22ΩI R R 24Ω(a)(b)图 2.2解：（1）对图（a ），R 1和恒压源并联，对图（b ），R 1和恒流源串联，它们都不是电源的内阻。

（2）对图（a ）：212U U V ==，2221234U I A R === 对图（b ）：22sI IA ==，222248U I R V ==⨯=（3）改变R 1对I 2和U 2均无影响。

I s （4）对图（a ）：2112356U I I A R =+=+= 对图（b ）：1226820s U I R U V =+=⨯+=(5) 改变R 1对（4）中的I 和U 均有影响，R 1增大则图（a ）中I 减小，图（b ）中U增大。

3．在图2.3所示的两个电路中，（1）负载电阻R L 中的电流I 及其两端电压U 各为多少？如果在图（a ）中除去（断开）与理想电压源并联的理想电流源，在图（b ）中除去（短接）与理想电流源串联的理想电压源，对计算结果有无影响？（2）判别理想电压源和理想电流源何者为电源，何者为负载？（3）试分析功率平衡关系。

(a)(b)R L ΩR L 2Ω图 2.3解：（1）对图（a ）：1052L U I A R ===，10U V = 对图（b ）：2I A =，224L U IR V ==⨯=如果在图（a ）中除去理想电流源，在图（b ）中除去理想电压源，对计算结果无任何影响。

K解)(6A=闭合时: 总电阻Ω=+⨯+=463632R)(5.7430301ARI===此时电流表的读数为:)(55.7326361AII=⨯=+=2-2 题2-2图示电路，当电阻R2=∞时，电压表12V；当R2=10Ω时，电压表的读数为4V，求R1和U S的值。

解:当∞=2R时可知电压表读数即是电源电压SU..12VUS=∴当Ω=102R时,电压表读数:41210101212=⨯+=+=RURRRuS(V)Ω=∴201R2-3 题2-3图示电路。

求开关K打开和闭合情况下的输入电阻R i。

解：K )(18.60//(10Ω+=∴i RK)(8//30//(10Ω==∴i R2-4 求题2-3图示电路的等效电阻R ab 、R cd 。

解：电路图可变为：)(154882.214882.2148//82.21)4040//10//(80//30)(08.1782.294082.294082.29//40)80//3040//10//(40)(4020800)(8010800)(402080020201020202010123123Ω=+⨯==+=Ω=+⨯==+=Ω==Ω==Ω==⨯+⨯+⨯=cdab R R R R R 2-5 求题2-5图示电路的等效电阻 R ab 。

题2-59ΩΩΩ解：(a)图等效为：5k Ω4k Ω 4k Ω8k Ωab5k Ω2k Ω8k Ωab)(73.315568787)25//(8Ω==+⨯=+=∴ab R (b)图等效为： 5Ω5Ω15Ω ab3Ω)(963251503101510153)55//(153Ω=+=+=+⨯+=++=∴ab R(c)图等效为：ba9Ω10Ω5Ω2Ω 4Ω8Ω 注意到54210⨯=⨯，电桥平衡，故电路中9电阻可断去)(67.127147148)25//()410(8Ω=+⨯+=+++=∴ab R (d)图等效为：ba54Ω14Ω R 12R 23R 31)(36186481818981818912Ω==⨯+⨯+⨯=R)(2272//)36//1436//54()(722)(3612311223Ω=+=Ω==Ω==ab R R R R R2-6 题2-6图示电路中各电阻的阻值相等，均为R ，求等效R ab .(b)(a)题2-6图解：e 、f 、g 电位点,所以 (a)图等效为：)]//()(//[)(R R R R R R R R R R R ab +++++++=RR R R R R R 45310//2]4//22//[2==+=(b)图等效为：])//()(//[)//()(R R R R R R R R R R R ab ++++++=RRR R R R R R R R 75.0433//)2//22//(2//22===+=2-7 化简题2-7图示各电路.245V 1028-836-解： （注：与电流源串联的元件略去，与电压源并联的元件略去）(a)图等效为：234-(b)图等效为：15-(d)图等效为：76-(e)图等效为：872-(f)图等效为：226V-2-8 用电源等效变换法求题2-8图示电路中负载R L上的电压U.+-14-2解：电路等效为：+ -7U+ -55-U+ -15-U+ -5+ -13+-U+-2.5)(3105.725.22VU=⨯+=2-9 题2-9图示电路.用电源等效变换法求电流i.3解：31A1A55-)(412051055105A i -=-=++-=∴2-10 若题2-10图示电路中电流i 为,问电阻R 的值是多少6-题2-10图解：流过R 的电流为i R =i -2== (A )，再利用电源等效变换，原电路等效为：2A4Ω12A13A3ΩRi R11Ai ’4Ω//3Ωi RR其中3Ω712)(712Ω=∴Ri 0(b)4ΩR 1(a)12-3Ω2Ω6Ω0.5i 0u S-+ u x -R 2 gu xbaba题2-11图解：(a)图等效为：i 04Ω3Ω 2Ω6Ω0.5i 0ba4i 04Ω2Ω2Ω0.5i 0ba148-2a8-4ba2ba224-iab2 ab-1 1 ab(b)图：设端口电流为i ，则01=++i gu R u x x i gR R u x 111+-=∴ 原电路变为：aa1112111)1(gR R gR gR R +=+-+ 2-12 求题2-12图示电路中电流源和电压源提供的功率分别是多少2Ω解：电流源发出功率为)(20102w P =⨯=原图可变为：ΩΩ2A2.21Ω2A)(21.221.11)9141142//(9141)2//76//221//(7//21)(7),(221),(73323233231312Ω=+=++=++=∴Ω=Ω=Ω=⨯+⨯+⨯=总R R R R)(32.452w R U P ==∴总总∴电压源发出的功率P ==(w )2-13 求题2-13图示电路a 、b 端的等效电阻R ab .Ω解：原电路等效为：1ΩΩ0.5ΩΩ)(35.22047)67//21(2Ω==+=∴ab R。

习 题 22.1 电路如图2.1所示，1k ΩR =，测得D 5V U =，试问二极管VD 是否良好（设外电路无虚焊）？解：内部PN 结或电极已开路，D 已损坏。

2.2 电路如图2.2所示，二极管导通电压D(on)U 约为0.7V ，试分别估算开关断开和闭合时输出电压o U 的数值。

图2.1 习题2.1电路图 图2.2 习题2.2电路图解： S 断开：断开VD ，D 5V U =。

所以VD 导通，o 50.7 4.3V U =-=S 闭合：断开VD ，)V (1125D-=⨯+-=RR RU ，所以VD 截止，o 6V U = 2.3 分析判断图2.3所示各电路中二极管是导通还是截止，并计算电压ab U ，设图中的二极管都是理想的。

图2.3 习题2.3电路图解：（a ）断开VD ，U D =5+5=10V>0，VD 导通 ，ab 5V U =-；（b）断开VD，D2151V23U=-⨯=-+，VD截止ab252V23U=⨯=+；（c）断开VD1 VD2，D1D212V,5127VU U==-+=，所以VD1优先导通，U D2= −5V，VD2截止，U ab=0V；(d) ）断开VD1 VD2，D1D212V,12517VU U==+=所以 VD2优先导通，D15VU=- VD1截止，ab5VU=-2.4 一个无标记的二极管，分别用a和b表示其两只引脚，利用模拟万用表测量其电阻。

当红表笔接a，黑表笔接b时，测得电阻值为500。

当红表笔接b，黑表笔接a时，测得电阻值为100k。

问哪一端是二极管阳极?解：b端是阳极2.5 二极管电路如图 2.4(a)所示，设输入电压i()u t波形如图 2.4(b)所示，在05mst<<的时间间隔内，试绘出输出电压o()u t的波形，设二极管是理想的。

图2.4 习题2.5电路图解：i()2tu t=，断开VD，D6iu u=-，当Du>时，VD导通，即3st>，60.2630.20.2iouu t-=⨯+=++当Du<时，VD截止，即3st<，6Vou=()ou tt/ms2.6 在图2.5所示的电路中，设二极管为理想的，已知i30sin(V)u tω=，试分别画出输出电压ou的波形，并标出幅值。