当前位置：文档之家 › 第二章电路的基本分析方法1

第二章电路的基本分析方法1

  • 格式：docx
  • 大小：1.74 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

(完整版)第二章电路分析方法

(完整版)第二章电路分析方法

第二章电路的分析方法电路分析是指在已知电路构和元件参数的情况下，求出某些支路的电压、电流。

分析和计算电路可以应用欧姆定律和基尔霍夫定律，但往往由于电路复杂，计算手续十分繁琐。

为此，要根据电路的构特点去寻找分析和计算的简便方法。

2．1 支路电流法支路电流法是分析复杂电路的的基本方法。

它以各支路电流为待求的未知量，应用基尔霍夫定律（KCL 和KVL ）和欧姆定律对结点、回路分别列出电流、电压方程，然后解出各支路电流。

下面通过具体实例说明支路电流法的求解规律。

例2-1】试用支路电流法求如图2-1 所示电路中各支路电流。

已知U S1 130V ，U S2 117V ，R1 1 ，R2 0.6 ，R 24 。

【解】该电路有3 条支路（b=3），2个结点（n=2）,3 个回路（L=3 ）。

先假定各支路电流的参考方向和回路的绕行方向如图所示。

因为有3 条支路则有3 个未知电流，需列出3 个独立方程，才能解得3个未知量。

根据KCL 分别对点A、B 列出的方程实际上是相同的，即结点A、B 中只有一个结点电流方程是独立的，因此对具有两个结点的电路，只能列出一个独立的KCL 方程。

再应用KVL 列回路电压方程，每一个方程中至少要包含一条未曾使用过的支路（即没有列过方程的支路）的电流或电压，因此只能列出两个独立的回路电压方程。

根据以上分析，可列出3 个独立方程如下：结点A I1 I2 I 0回路ⅠI1R1 I2R2 U S1 U S2回路ⅡI2 R2 IR U S2I1 10A， I2 5A， I=5A 联立以上3 个方程求解，代入数据解得支路电流通过以上实例可以总出支路电流法的解题步骤是：1．假定各支路电流的参考方向，若有n个点，根据KCL 列出（n－１）个结点电流方程。

２．若有b 条支路，根据KVL 列（b－n＋１）个回路电压方程。

为了计算方便，通常选网孔作为回路。

5 3．解方程组，求出支路电流。

【例 2-2】如图 2-2 所示电路，用支路电流法求各支路电流。

第二章电路的分析方法（答案）

第二章电路的分析方法（答案）

第⼆章电路的分析⽅法（答案）第⼆章电路的分析⽅法本章以电阻电路为例，依据电路的基本定律，主要讨论了⽀路电流法、弥尔曼定理等电路的分析⽅法以及线性电路的两个基本定理：叠加定理和戴维宁定理。

1．线性电路的基本分析⽅法包括⽀路电流法和节点电压法等。

（1）⽀路电流法：以⽀路电流为未知量，根据基尔霍夫电流定律（KCL）和电压定律(KVL)列出所需的⽅程组，从中求解各⽀路电流，进⽽求解各元件的电压及功率。

适⽤于⽀路较少的电路计算。

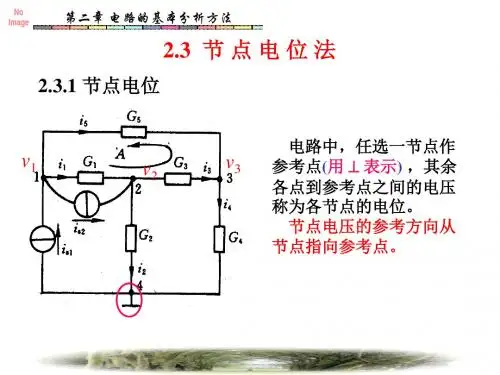
（2）节点电压法：在电路中任选⼀个结点作参考节点，其它节点与参考节点之间的电压称为节点电压。

以节点电压作为未知量，列写节点电压的⽅程，求解节点电压，然后⽤欧姆定理求出⽀路电流。

本章只讨论电路中仅有两个节点的情况，此时的节点电压法称为弥尔曼定理。

2 ．线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理，是分析线性电路的重要定理，也适⽤于交流电路。

（1）叠加定理：在由多个电源共同作⽤的线性电路中，任⼀⽀路电压（或电流）等于各个电源分别单独作⽤时在该⽀路上产⽣的电压（或电流）的叠加（代数和）。

①“除源”⽅法（a）电压源不作⽤：电压源短路即可。

（b）电流源不作⽤：电流源开路即可。

②叠加定理只适⽤于电压、电流的叠加，对功率不满⾜。

（2）等效电源定理包括戴维宁定理和诺顿定理。

它们将⼀个复杂的线性有源⼆端⽹络等效为⼀个电压源形式或电流源形式的简单电路。

在分析复杂电路某⼀⽀路时有重要意义。

①戴维宁定理：任何⼀个线性含源的⼆端⽹络，对外电路来说，可以⽤⼀个理想电压源和⼀个电阻的串联组合来等效代替，其中理想电压源的电压等于含源⼆端⽹络的开路电压，电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。

②诺顿定理：任何⼀个线性含源的⼆端⽹络，对外电路来说，可以⽤⼀个理想电流源和⼀个电阻的并联组合来等效代替。

此理想电流源的电流等于含源⼆端⽹络的短路电流，电阻等于该⼆端⽹络中全部独⽴电源置零以后的等效电阻。

3 ．含受控源电路的分析对含有受控源的电路，根据受控源的特点，选择相应的电路的分析⽅法进⾏分析。

第2章 电路分析基础(张永瑞)(第三版)

第2章 电路分析基础(张永瑞)(第三版)

为 i1, i2, i3, 其参考方向标示在图上。就本例而言，问题是如
何找到包含未知量 i1, i2, i3 的 3个相互独立的方程组。
第二章 电路的基本分析方法
图 2.1-2 支路电流法分析用图
第二章 电路的基本分析方法
根据KCL，对节点 a 和 b 分别建立电流方程。设流出
节点的电流取正号，则有
第二章 电路的基本分析方法
解出支路电流之后，再要求解电路中任何两点之间的电 压或任何元件上消耗功率那就是很容易的事了。例如， 若再要求解图 2.1-2 电路中的 c 点与 d 点之间电压ucd 及 电压源 us1所产生的功率 Ps1，可由解出的电流i1、i2、i3 方 便地求得为
ucd R1i1 R2i2 ps1 us1i1
i1 i2 i3 0
(2.1-7)
(2.1-7)式即是图2.1-2 所示电路以支路电流为未知量的足够的 相互独立的方程组之一，它完整地描述了该电路中各支路电 流和支路电压之间的相互约束关系。应用克莱姆法则求解 (2.1-7)式。系数行列式Δ和各未知量所对应的行列式Δj(j=1, 2,
个节点列KCL方程时，规定流出节点的电流取正号，流入节
点的电流取负号，每一个支路电流在n个方程中一定出现两 次， 一次为正号(+ij), 一次为负号(-ij), 若把这n个方程相加，
它一定是等于零的恒等式，即
第二章 电路的基本分析方法
( i ) [( i ) ( i )] 0
第二章 电路的基本分析方法
2.1.2 独立方程的列写
一个有n个节点、b条支路的电路，若以支路电流作未知
变量， 可按如下方法列写出所需独立方程。
(1) 从 n 个节点中任意择其n-1个节点，依KCL列节点电

电工学 第二章 电路的分析方法

电工学 第二章 电路的分析方法
返回
例4、用叠加原理求图示电路中的I。 1mA 4kΩ + 10V － 2kΩ I 2kΩ
2kΩ
解:
电流源单独作用时 电压源单独作用时: 10 2 44 mA 1 257mA II 1 mA .0.25mA 4 2 [2+4//2] 4 4 2 [(2+2)//2] 2 I=I′+I″= 1.507mA
返回
第三节 电压源与电流源的等 效变换
等效变换的概念 二端电阻电路的等效变换 独立电源的等效变换 电源的等效变换 无源二端网络的输入电阻 和等效电阻
返回
一、等效变换的概念
1、等效电路
两个端口特性相同，即端口对外的 电压电流关系相同的电路，互为等效电 路。
返回
2、等效变换的条件 对外电路来说，保证输出电压U和 输出电流I不变的条件下电压源和电流 源之间、电阻可以等效互换。
1 1 2 2 S
－US＋R2I2＋R3I3＋R4I4 ＝0
返回
第二节 叠加原理
叠加原理
原理验证
几点说明
返回
一、叠加原理
在由多个 独立电 源共同 作用的 线性 电路中,任一支路的电流(或电压)等于各 个独立电源分别单独作用在该支路中产 生的电流(或电压)的叠加(代数和) 。
不作用的恒压源短路,不作用的恒流 源开路。
US2单独作用
= 4/3A
返回
三、几点说明
叠加原理只适用于线性电路。
电路的结构不要改变。将不作用的恒压
源短路，不作用的恒流源开路。
最后叠加时要注意电流或电压的方向:
若各分电流或电压与原电路中电流或
电压的参考方向一致取正，否则取负。 功率不能用叠加原理计算。

第二章 电路的分析方法

第二章 电路的分析方法

电路分析基础
回路电流法求解电路的步骤
选取自然网孔作为独立回路,在网孔中标出各回路电流
的参考方向,同时作为回路的绕行方向; 支路上的互阻压降由相邻回路电流而定;
建立各网孔的KVL方程,注意自电阻压降恒为正,公共 联立求解方程式组,求出各假想回路电流. .
它们与回路电流之间的关系,求出各支路电流.
返节目录
电路分析基础
思考 练习
用结点电压法求解下图所示电路,与回路电流法相比较, 能得出什么结论? US3 R I A+ - 3 3 B
IS1 I1
R1
I4
R4
I5
R5
I2
R2
IS2
此电路结点n=3,用 结点电压法求解此电 路时,只需列出3-1=2 个独立的结点电压方 程式:
U S3 1 1 1 1 ( + + )V A V B = I S1 + R1 R 3 R 4 R3 R3 ( U 1 1 1 1 + + )V B V A = I S2 S3 R 2 R3 R5 R3 R3
返节目录
电路分析基础
结点电压法应用举例
用结点电压法求解结点n=2的复杂电路时,显然只需 列写出2-1=1个结点电压方程式,即: US
例
① I2 R2 + US2 _ I3 R3 I4 R4
-
V1 =
∑R ∑
S
I1 R1 + US1 _
1 R
+
US4
此式称弥尔曼 定理.是结点 电压法的特例
直接应用弥尔曼定理求V1
返节目录
电路分析基础
第1节 支路电流法
定义
以支路电流为未知量,根据基尔霍夫两定律列出必 要的电路方程,进而求解客观存在的各支路电流的方 法,称支路电流法 支路电流法.

第2章 第1、2节 电路的分析方法

第2章 第1、2节 电路的分析方法

第二节 电压源和电流源
六、几种特殊情况
+
E1 E2
+ +
-
-
-
E
Is1 IS2
Is
+
+
R
R
E
-
-
E
Is
Is
第二节 电压源和电流源
六、几种特殊情况
+ Is E
+
Is
+
E
Is
-
-
E
-
第二节 电压源和电流源
七、例题 P18 例2 —4
八、作业
1、P31
2 —7
第二节 电压源和电流源
2、有两个直流电压源并联向负载电阻RL=9Ω供 、有两个直流电压源并联向负载电阻R =9Ω 电，如图示。E =120V， =2Ω 电，如图示。E1=120V，R01=2Ω,E2=240V， 240V， R02=2Ω。求负载RL上流过的电流IL。 =2Ω。求负载R + E1 R01 + R02 IL E2 R L
第二节 电压源和电流源
2、理想电压源 2）特点 流过外电路的电流是由外电路决定。 3）理想电压源的电路符号及伏安特性
+ E － 0
I U
R
U
E
U=E I
第二节 电压源和电流源
理想电压源的伏安特性表明：负载电阻发 生变化时，负载电流发生变化，但端电压 始终保持不变。
第二节 电压源和电流源
3、实际电压源 理想电压源是不存在的，任何电源都有内阻。实 际电压源可视为由一个理想电压源和一个内阻串 联而成。 1）符号
第二节 电压源和电流源
四、电流源的并联
a R01 R02 R03 R0 b

第2章23节点电位法

第2章23节点电位法

is3 32 5 A
G 1 1 3 47 S ,
G 1 2 3 S ,
G 1 3 4 S
G 2 1 3 S ,
G 2 2 1 2 36 S ,
G 2 3 2 S
G 3 1 4 S ,
G 3 2 2 S ,
G 3 35 2 4 1 1 S
is 1 1 3 8 1 1 A ,
( G 1 G 5) v 1 G 1 v 2 G 5 v 3 is 1 is2 G 1 v 1 ( G 1 G 2 G 3) v 2 G 3 v 3 is2 G 5 v 1 G 3 v 2 ( G 3 G 4 G 5) v 3 0
( G 1 G 5 ) v 1 G 1 v 2 G 5 v 3 is 1 is 2 G 1 v 1 ( G 1 G 2 G 3 ) v 2 G 3 v 3 is 2 G 5 v 1 G 3 v 2 ( G 3 G 4 G 5 ) v 3 0
化简： 3 11 v1 4 v2 2

3 4
v1

9 10
v2


21

10
注意:列写方程时电阻要换算为电导。
No Image
第二章 电路的基本分析方法

v1 v 4 2

电压源支 路的电流
1 2

1 1

v
1

1 2
v2

ix


1 2
v1


1 2

1 2

v
2

1 2 v4

4


1 2 v2

第二章(1)电路基本分析方法

第二章(1)电路基本分析方法

I3
U s1
R1
R2
I2
②
U s3
R3
①
1
3
2
②
2.1.1 电路图与拓扑图
②
R2
① R3
R4
R5
③
R6 ④
U s1
R1
实际电路图
②
2
4
①
5
③
3
6
④
1
对应的线图
线图是由点（节点）和线段（支路）组成，反映实际 电路的结构（支路与节点之间的连接关系）。
有向图
如果线图各支路规定了一个方向（用 箭头表示，一般取与电路图中支路电流 方向一致），则称为有向图。
回路2：I3×R3＋US3－I4×R4＋I2×R2=0
回路3：I4×R4＋I6×R6－I5×R5=0
网孔回路电压方程必为独立方程。
网孔回路电压方程数=b（支路数）－n（节点数）＋1
解出支路电流
4>. 由n­1个节点电流方程和b­n+1个网孔电压方程（共b
个方程）可解出b个支路电流变量。
R3
I 3
U s3
第二章(1) 电路基本分析方法
本章内容
1.网络图论初步 2.支路电流法 3.网孔电流法 4.回路电流法 5.节点电压法
2.1 网络图论的概念
图的概念：对于一个由集中参数元件组成的电网络，
若用线段表示支路，用黑圆点表示节点，由此得到一
个由线条和点所组成的图形，称此图为原电网络的拓
扑图，简称为图。
I1 ①
－ I1 ＋ I2 － I3 =0
I1 －10＋3× I2 =0 3×I2 ＋2× I3 －13=0
解得： I1 =1A， I2 =3A， I3 =2A

电路分析第2章 电路分析方法1

电路分析第2章 电路分析方法1

i2 G3 4
结论： 结论： 1. 自电导×节点电压 + 互电导×相邻节点电压 = 该节点 自电导× 互电导× 的电流源电流代数和。流进为正，流出为负。 的电流源电流代数和。流进为正，流出为负。 2. 自电导均为正值，互电导均为负值。 自电导均为正值，互电导均为负值。 3.适用于平面电路和非平面电路。 适用于平面电路和非平面电路。 适用于平面电路和非平面电路
( R1 + R3 ) I1 − R3 I3 = U S1 − U 0 ( R4 + R5 + R6 ) I2 − R6 I3 = U 0 − R3 I1 − R6 I2 + ( R2 + R3 + R6 ) I3 = U S2 I S = I 2 − I1
辅助方程
10
[例4] 电路如图示，已知 S=5V，R1=R2=R4=R5=1Ω， 例 电路如图示，已知U ， Ω R3=2Ω，µ=2。 求U1＝？ Ω 。 R5 +µU2– [解] 列网孔方程时，可先将受控源 解 列网孔方程时，
应用KVL列回路电压方程 列回路电压方程 应用 R2iB+R5(iA+iB)+R6(iB+iC) − uS2 =0
+
R1iA+R5(iA+iB)+R4(iA−iC) + uS4 − uS1=0 R3iC− uS3 − uS4+R4(iC−iA)+R6(iB+iC) =0
uS3
–
R3
i3
(R1+R4+R5)iA+R5iB−R4iC = uS1 − uS4 R11iA+R12iB+R13iC=uS11 R21iA+R22iB+R23iC=uS22 R5iA+ (R2+R5+R6)iB+R6iC = uS2 −R4iA+R6iB+(R3+R4+R6)iC= uS3+uS4 R31iA+R32iB+R33iC=uS33

电工技术 第二章电路的分析方法

电工技术 第二章电路的分析方法

戴维南定理和诺顿定理
总结词
戴维南定理和诺顿定理是两种等效电源定理，它们可 以将复杂电路简化为一个等效的电源和一个电阻的串 联或并联形式，从而简化电路分析。
详细描述
戴维南定理将一个线性有源二端网络等效为一个电压 源和一个电阻的串联形式，其中电压源的电压等于二 端网络的开路电压，电阻等于网络内部所有独立源为 零时的等效电阻。诺顿定理则将有源二端网络等效为 一个电流源和一个电阻的并联形式，其中电流源的电 流等于网络的短路电流，电阻与戴维南定理中的电阻 相同。这两种定理在电路分析中有着广泛的应用。
最大功率传输定理
总结词
最大功率传输定理是关于电路中最大功率传输的条件和规律的定理。它表明在一定的电源内阻和负载 电阻条件下，负载电阻可以吸收的最大功率是一定的，且该最大功率发生在负载电阻等于电源内阻时 。
详细描述
最大功率传输定理是分析功率传输问题的基础，它可以帮助我们了解在给定电源内阻和负载电阻的情 况下，如何选择合适的负载电阻以获得最大的功率传输效率。这对于电子设备和系统的设计具有重要 的指导意义。
非线性电容和电感电路的分析
总结词
非线性电容和电感电路是指电容和电感值随电压或电流变 化的电路，其分析方法主要包括等效法和状态变量法。
详细描述
等效法是通过简化电路来分析非线性电容和电感电路的方 法，而状态变量法则通过建立状态方程来求解非线性电容 和电感电路的解。
总结词
在分析非线性电容和电感电路时，需要注意非线性元件的 特性变化和电路的稳定性，以确定电路的工作状态和性能 。
电路的基本物理量
电流
单位时间内通过导体横截面的电荷量， 用符号“I”表示，单位为安培（A）。
电阻
表示导体对电流阻碍作用的物理量， 用符号“R”表示，单位为欧姆 （Ω）。

电路分析基础(张永瑞)第三版 第二章课后习题

电路分析基础(张永瑞)第三版 第二章课后习题

节点c i3 i i5 0 4
由KVL列方程 回路Ⅰ 2i1 3i2 2i6 15 0 回路Ⅱ 3i3 9 3i4 3i2 0 回路Ⅲ 3i4 1 i5 5 2i6 0
•
2.2-3 对图示电路，试列出求解该电路的网孔方程组。 解 设网孔电流 iA、iB、iC 如图中所标，观察电路，对照网孔方程通式 列写求解该电路的网孔方程组为
R1 R7 R6 R5 iA R7iB R6 R5 iC us1 us 4 R7iA R2 R7 R8 iB R8iC us 2 R5 R6 iA R8iB R3 R5 R6 R8 R4 iC us 3 us 4
•
2.1 图示电路，求支路电流 I1 , I 2, I 3 。 解 设网孔电流 I A、I B 如图中所标。列网孔方程为
18 I A 11I B 64 11I A 18 I B 6
(1) (2)
应用克莱姆法则求解以上方程组
A B
18 11
11 18
203
(1) (2)
4va 3vb 6 2va 3vb 0
va 3V，vb 2V
4 vb 4 2 i 1A 2 2
P 4va 4 3 12W 1 P2 2vab 2 (3 2) 2W P3 4vb 4 2 8W P4 U s 4i 4 1 4W
7v1 2v2 12 4v1 7v2 12


•
2.3-4 求如图所示电路中各 电源产生功率。 解 设节点a、b、c如图所标， 且选节点c作参考点(接地)，节点a、 b的电位分别为 观察电路， va、vb。 对照节点方程通式列写节点方程为

第2章 电路的分析方法

第2章 电路的分析方法

此方法特别适合结点少支路多的电路。 方法特别适合结点少支路多的电路。
28
例
用结点电压 法求图示电路 中的电流I。
1）选择参考结点， 选择参考结点，标 出结点电压与支路电流 的正方向。 的正方向。 2）列结点电压方程组
1 1 1 1 28 + )U 1 − U 2 = ( + 10 40 20 20 10 1 1 1 − U 1 + ( + )U 2 = 5 20 20 30
1 r1 r2 2 r3 3
Y-∆
等效变换 R12 2
1 R31 R23 3
当 r1 = r2 = r3 =r , R12 = R23 =R31 =R 时：
1 r= R 3
8
4、实际电源模型间的等效互换
一个实际电源既可用电压源与电阻串联 一个实际电源既可用电压源与电阻串联的电 电压源与电阻串联的电 路模型来表示， 路模型来表示，也可用电流源与电阻并联 也可用电流源与电阻并联的电路 电流源与电阻并联的电路 ' 模型来表示。 模型来表示。即 I I a a RO ' Uab + Uab ' RO US IS b b 等效互换的条件： 等效互换的条件：对外的电压电流相等。 对外的电压电流相等。 即： '
3)求I
U1 − U 2 I= = −2.2 A 20
29
解得 U1=40V , U2=84V
例
电路如图所 示，求电路结点 2的电位V2。 分析 V1＝2V
I2
I1
解：
1 3 1 1 + V2 − V1 = − + 0.5 3 3 3 4
解得： 解得： 验证： 验证： V2＝2/7 V=0.29V

电工技术--第二章 电路的分析方法

电工技术--第二章 电路的分析方法
I1
A
R1 Us1 R2
I2
R3 Us2 B
I3
A
I1 '
A
I2' I1"
R1 Us1
R2
R1
R2
I2"
R3
I3'
+
R3 Us2
I3 "
B
B
A
I1
R1 R2
A
I2
R3
A
I2'
R3
I1' I3
R1
R2
I1" I3'
R1
R2
I2"
R3
Us1 Us2
=
Us1
+
Us2
I3"
B
B
B
解： I1
U S1 R 2R 3 R1 + R2 + R3
例1 ：
I1 R1 I3
a
I2 R2 R3 2 +
对结点 a： I1+I2–I3=0 对网孔1： I1 R1 +I3 R3=E1 E2 对网孔2： I2 R2+I3 R3=E2
+ E1
-
1
-
b
联立求解各支路电流
例：试求各支路电流。
a
c
支路中含有恒流源 I3 注意：当支路中含有恒流源 时，若在列KVL方程时，所选 回路中不包含恒流源支路
+
U -
I RL
Ro Uo
+
+ _
I RL
网络
U B
B 有源二端网络
戴维南等效电路
任意一个线性有源二端网络对外都可等 效为等效电压源。

第二章 电路的基本分析方法1

第二章 电路的基本分析方法1

第二章电路的基本分析方法一、填空题：1. 有两个电阻，当它们串联起来的总电阻为10Ω，当他们并联起来的总电阻为2.4Ω。

这两个电阻的阻值分别为_ _4Ω ___和__6Ω。

= 1 Ω。

2. 下图所示的电路，A、B之间的等效电阻RAB= 3 Ω。

3. 下图所示的电路，A、B之间的等效电阻RABA2ΩB4. 下图所示电路，每个电阻的阻值均为30Ω，电路的等效电阻R= 60ABΩ。

5.下图所示电路中的A、B两点间的等效电阻为___12KΩ________.若图中所示的电流I=6mA，则流经6K电阻的电流为__2mA _____；图中所示方向的电压U为____12V____.此6K电阻消耗的功率为__24mW_________。

AU6. 下图所示电路中，ab 两端的等效电阻为 12Ω，cd 两端的等效电阻为 4Ω 。

abcd6Ω5Ω15Ω5Ω7．下图所示电路a 、b 间的等效电阻Rab 为 4 Ω。

8. 下图所示电路中，ab 两点间的电压abU 为 10 V 。

+_++_10V4V 24V a b9. 下图所示电路中，已知 U S =3V ， I S = 3 A 时，支路电流I 才等于2A 。

_+Ω1ΩsI 3I10. 某二端网络为理想电压源和理想电流源并联电路，则其等效电路为 理想电压源 。

11．已知一个有源二端网络的开路电压为20V ，其短路电流为5A ，则该有源二端网络外接 4 Ω电阻时，负载得到的功率最大，最大功率为 25W 。

12．应用叠加定理分析线性电路时，对暂不起作用的电源的处理， 电流 源应看作开路， 电压 源应看作短路。

13．用叠加定理分析下图电路时，当电流源单独作用时的I 1= 1A ，当电压源单独作用时的I 1= 1A ，当电压源、电流源共同时的I 1= 2A 。

+_Ω6I 13A9V 3Ω14．下图所示的电路中，（a ）图中Uab 与I 的关系表达式为 Uab= 3I ，(b) 图中Uab 与I 的关系表达式为 Uab=3I+10 ，(c) 图中Uab 与I 的关系表达式为 Uab=6(I+2)-10 ，（d ）图中Uab 与I 的关系表达式为 Uab=6(I+2)-10 。

第2章-电路分析全解

第2章-电路分析全解
《电路分析简明教程》

第二章
本章中心内容


本章介绍线性电路的三类基本分析方法： 等效分析法─将复杂结构的电路化为简单结构的 电路。 方程分析法─选择不同的电压和电流作为求解变 量，利用系统的方法列出描述电路的方程。 叠加分析法─运用线性电路的叠加性质分析电路， 使含有多个激励的电路化简为单一激励电路。
第二章 线性电路分析的基本方法
§2-1 电路的等效变换 §2-2 支路电流分析法 §2-3 网孔电流分析法 §2-4 节点电压分析法 §2-5 叠加定理 §2-6 置换定理 §2-7 戴维宁定理和诺顿定理 *§2-8 不含独立源的双口网络的等效电路 *§2-9 应用实例 *§2-10 计算机仿真分析线性电阻电路 本章学习要求
二、网孔电流法 以网孔电流为求解变量，根 据KVL和元件VAR对网孔列出 电压方程，以求解电路的方法 iM1 iM2 称为网孔电流法。 如图所示电路中，设网孔的绕行 方向与网孔电流方向相同。 根据KVL和元件VAR列写网孔的电压方程如下： 网孔1 R1iM1+R2(iM1-iM2)－us1=0 网孔2 R3iM2－R2(iM1-iM2)+us2=0 整理得 （R1+R2）iM1－R2iM2= us1 －R2iM1+(R2+R3)iM2=－us2
(a)
(b)
(c)
(d) 《电路分析简明教程》

§ 2- 1
由图(d)得
-U 6 1 (2 1) I 0 I 1 U
(d)
U ( 6 1 1)V 1V 2 2 1
《电路分析简明教程》

例2 求图(a)所示电路的电流i。
§ 2- 1

§ 2- 1

第二章 电路的分析方法

第二章 电路的分析方法
3. 联立求解得： I、I1、I 2、I 3、I 4、I G
支路电流法的优缺点:
优点：支路电流法是电路分析中最基本的 方法之一。只要根据基尔霍夫定律、欧 姆定律列方程，就能得出结果。
缺点：电路中支路数多时，所需方程的个 数较多，求解不方便。
a
支路数 =4
b
需列4个方程式
2.5、节点电压法
节点电压的概念：
U –
R1
R2
● 各电阻两端的电压相同；
11 1
等效：
R R1 R2
电流分配关系：
或：G G1 G2
G为电导，单位S
I
+ U –
● 并联电阻上电流与电阻大小成反比。
两电阻并联时的分流公式：
R
I1
R2 R1 R2
I
I2
R1 R1 R2
I
电阻等效变换举例：
利用串并联变换 I
利用对称性(相同电位短接）
2、列写方程步骤： A
E1
1 E2
2
-
-
I3 R3
R1 I1
R2 I2
B
1）在图中标注各支路电流及正方向； 2）选定回路（可按网孔）并标注绕行方向； 3）由节点：列写（n-1）个独立的节点电流方程； 4）由回路：列写 b-(n-1) 个独立的回路电压方程； 5）联立求解出各支路电流； 6）进而求去其它电量。
以支路电流为自变量列写的KCL方程和KVL方程， 联立求解的方法。
求出各支路电流之后，进而可以求出其他量。
注意：
●若电路中有 b 条支路（b个支路电流未知数），共需列b个独 立方程才能求解。 ●若电路中有n个节点，
用KCL可列（n-1）个独立的电流方程。 用KVL可列 b-(n-1) 个独立的电压方程(即“网孔数”)。

第2章 电路的分析方法1.电路的连接2.电压源和电流源3.支路电...

第2章 电路的分析方法1.电路的连接2.电压源和电流源3.支路电...

U U R1 U 1 R1 I R1 R1 U R R1 R2 R1 R2 两个电阻串联时的分压公式：
R1 U1 U R1 R2
I + U – + U1 R1 – + U2 R 2 –
R2 U2 U R1 R2
I + U – R
8
第2章
电路的分析方法
例 2-1 有一个电表的表头，其内阻R g=5kΩ，允许 通过的最大电流（这时表头指针偏转到满刻度） I g =200μA. 。问直接用这个表头可以测多大的电压？ 如果要求用来测量 10V以下（包括 10V）的电压， 则应串入多大的电阻？
4
第2章
电路的分析方法
电阻的串联和并联
一、电阻的串联：
Req R1 R2 Rn Rk
k 1 n
二、电阻的并联：
n 1 1 1 1 1 Req R1 R2 Rn k 1 Rk
5
第2章
电路的分析方法
2.1 电阻的连接
在电阻电路中，电阻的连接形式多种多样，其中最简 单的连接方式是串联和并联 2.1.1 电阻的串联 几个电阻依次首尾相接，中间没有节点，不产生分支 电路，这种连接方式叫串联，其重要特点是在电源作 用下，串联电路中的电流是处处相等的。 1.串联电阻的等效化简 对于多个串联电阻来说，可以用一个等效电阻R来代 替，该等效电阻R可以用KVL很容易计算出来，等效 电阻的值等于串联电路中各电阻之和
R
+ U I I1 R1 R2 I2 + U 11
第2章
电路的分析方法
I
R1 R 2 R1 R 2
R
图 2-3 并联电阻的等效简化

第2章23节点电位法

第2章23节点电位法
1) 含有电压源与电阻串联的节点电位方程。 例1 如图所示电路中，列写各节点的电位方程。
注意：将电压源与电阻串联变换为电流源与电阻并联。
第二章 电路的基本分析方法
解：

11 55


11 22
11 2200

11 22

11 44
vv11

11 44
总结：节点法 分析具有 3 个 独立节点电路 的方程通式
G11v1 G12v2 G13v3 is11
G21v1

G22v2

G23v3

i
s
22

G31v1

G32v2

G33v3

i
s
33

流入节点 的电流源 为正，流 出为负。
n 个节点方 程的通式为
G11v1 G12v2 ... G1nvn is11
节点 电位 方程 组：
7v1 3v2 4v3 11
3v1 6v2 2v3 3

4v1 2v2 11v3 25
第二章 电路的基本分析方法
1.只含有一个元件的支路节点方程的列写
例1 求电导G1、G2、G3 中的电流及3个电流源分别产生的功率。 解： 看图说话，先写出自电导、互电导及电流源数值。

3 4
v1

9 10
v2


21 10
注意:列写方程时电阻要换算为电导。
第二章 电路的基本分析方法
2) 含有电流源与电阻串联的节点电位方程。 解:本电路 2、 43节点间有一理 想电流源与电阻的串联：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章电路的基本分析方法一、填空题：1. 有两个电阻，当它们串联起来的总电阻为10Ω，当他们并联起来的总电阻为2.4Ω。

这两个电阻的阻值分别为_ _4Ω ___和__6Ω。

= 1 Ω。

2. 下图所示的电路，A、B之间的等效电阻RAB= 3 Ω。

3. 下图所示的电路，A、B之间的等效电阻RABA2ΩB4. 下图所示电路，每个电阻的阻值均为30Ω，电路的等效电阻R= 60 Ω。

AB5.下图所示电路中的A、B两点间的等效电阻为___12KΩ________.若图中所示的电流I=6mA，则流经6K电阻的电流为__2mA _____；图中所示方向的电压U为____12V____.此6K电阻消耗的功率为__24mW_________。

AU6. 下图所示电路中，ab两端的等效电阻为 12Ω，cd两端的等效电阻为 4Ω。

7．下图所示电路a、b间的等效电阻Rab为 4 Ω。

8. 下图所示电路中，ab两点间的电压abU为 10 V。

9. 下图所示电路中，已知 US =3V， IS= 3 A 时，支路电流I才等于2A。

Ω1310. 某二端网络为理想电压源和理想电流源并联电路，则其等效电路为理想电压源。

11．已知一个有源二端网络的开路电压为20V，其短路电流为5A，则该有源二端网络外接 4 Ω电阻时，负载得到的功率最大，最大功率为 25W 。

12．应用叠加定理分析线性电路时，对暂不起作用的电源的处理，电流源应看作开路，电压源应看作短路。

13．用叠加定理分析下图电路时，当电流源单独作用时的I1= 1A ，当电压源单独作用时的I1= 1A ，当电压源、电流源共同时的I1=2A 。

14．下图所示的电路中，（a）图中Uab与I的关系表达式为 Uab= 3I ，(b) 图中Uab与I的关系表达式为 Uab=3I+10 ，(c) 图中Uab与I的关系表达式为 Uab=6(I+2)-10 ，（d）图中Uab与I的关系表达式为 Uab=6(I+2)-10 。

6Ω+_10V+_I2AU abba3Ω（a）(b) (c) （d）15. 下图所示的电路中，当9V的电压源单独作用时I= 1A ，当6A的电流源单独作用时I= -2A ，当电压源和电流源共同作用时I= -1A 。

16. 下图中电路的各电源发出的功率为UsP= 0 ，IsP= 8W 。

6Ω617. 如下图所示的一有源线性二端网络N，在端口a、b接入电压表时读数为10V，接入电流表时读数为5A，则其戴维宁等效电路的参数：开路电压ocU= 10 V，等效电阻eq R = 2 Ω。

ab18. 额定值为220V 、40W 的灯泡，接在110V 的电源上，其功率为 10 W 。

19. 如下图所示电路中18s i A =，21s i A =，33s i A =，电阻12R =Ω，23R =Ω，38R =Ω，则各支路的电流1i = 2 A ，2i = -7 A ，3i = 10 A 。

二、选择题：1. 某有源二端网络的开路电压为12V,短路电流2A,当外接12Ω的负载电阻时,其端电压为( C )｡A.3VB.6VC.8VD.9V2. 图示电路，用叠加原理求支路电流I 、S U 单独作用时的电流用I '表示，S I 单独作用时用I ''表示，则下列回答正确的是（ B ）。

A ．2A I '=，1A I ''=， 3A I =B ． 2A I '=，1A I ''=-， 1A I =C ． 1.5A I '=，2A I ''=， 3.5A I =D ．2A I '=，1A I ''=， 0.5A I =-3. 关于理想电压源或理想电流源，说法不正确的是( B )。

A. 理想电压源的内阻可以看成零，理想电流源的内阻可以看成无穷大B. 理想电压源的内阻可以看成无穷大，理想电流源的内阻可以看成零C. 理想电压源的输出电压是恒定的D. 理想电流源的输出电流是恒定的 4. 电流源开路时，该电流源内部（ A ）。

U 3AA.有电流，有功率损耗B.无电流，无功率损耗C.有电流，无功率损耗D.无电流，有功率损耗 5．下图所示电路，ab 端电压Ｕ＝( C )。

A. 15V B. 4V C. 5V D.14V6．下图所示电路中结点a 的结点方程为( C )。

A.15.07.1b a -=-U UB.15.07.1b a =+U UC.15.07.1b a =-U UD.a b 821U U -=7．下图所示电路，ab 间开路时的端电压Ｕ＝( C )。

A. 15Ｖ B. 4Ｖ C. 5Ｖ D. 10Ｖ8. 叠加定理不仅适用于线性电路中的电压，还适用于电路中的（ B ）。

A ．功率 B ． 电流 C ．能量 D.阻抗 9. 理想电压源的内阻为（ A ）。

A.0 B ．∞ C ．有限值 D ．由外电路来确定10. 下图所示电路中电流i 为（ C ）。

A.5A B ．0 C ．7A D ．3A11．电路如下图所示，对负载R 而言，虚线框的电路可用一个等效的电路代替，该电路是（ C ）。

A ．实际的电压源B ．理想的电压源C ．理想的电流源D ．不能确定R12．下图所示电路中，下列说法正确的是（ D ）。

A ．U S 、I S 都发出功率 ；B ．U S 、I S 都吸收功率；C ．U S 发出功率，I S 不一定；D ．I S 发出功率，U S 不一定。

+_U SI S纯纯纯纯纯10V2A13. 用叠加定理分析线性电路时，对那些暂不起作用的电压源可看作（ C ），而暂不起作用的电流源可看作（ A ）。

A. 开路 B ．电阻 C ．短路 D ．电容 14. 如下图所示的等效电阻R AB 为（ A ）。

A. 2ΩB.4ΩC. 5ΩD. 8ΩΩ15. 将110V/40W和110V/100W的两盏白炽灯串联在220V电源上使用，则（ C ）。

A．两盏灯都能安全、正常工作B．两盏灯都不能工作，灯丝都烧断C．40W灯泡因电压高于110V而灯丝烧断，造成100W灯灭D.100W灯泡因电压高于110V而灯丝烧断，造成40W灯灭16. 有一内阻可以忽略不计的直流电源，向互相串联的R1、R2输送电流。

当90Ω的电阻R1短路后，流过电路的电流是原来的4倍，则电阻R2的阻值是（ A ）。

A.30ΩB.60ΩC.180ΩD.260Ω17．要使三只“110V40W”灯泡接入电源电压为220V的电路中都能正常工作，那么这些灯泡应该是（ B ）。

A.全部串联B.每只灯泡串联适当电阻后再并联C.二只并联后与另一只串联D.二只串联后与另一只并联18．在下图中，所示的三个电阻的联接方式（ B ）。

A .R1与R3串联后与R2并联 B. R1与R3并联后与R2串联C. R1与R2并联后与R3串联D. R1与R2串联后与R3并联19.下图所示电路中，A.B间有4个电阻串联，且R2＝R4，电压表V1示数为12V，V 2示数为18V，则A.B之间电压UAB应是（ D ）。

A.6 VB.12 VC.18 VD.30 V20．下图所示电路中，AB两点间电压ABU ( A )。

A ．9 VB ． 12VC ． 20VD ．17V21． 理想电压源的内阻为( A )。

A ．0B ．∞C ．有限值D ．由外电路来确定 22． 下图所示电路中N 0为无源线性电阻网络，S I 恒为4A ，S U 的值可变。

当0s U =时, 26U =V ；当U S =8 V 时，电流源I S 不吸收也不产生功率；则当U S = 12 V 时，电流源吸收功率为( )。

A. 16 WB. 14 WC. 12 WD. 10 WUS23．下图中输入电阻ab R 与输出电阻cd R 的关系为( A )。

A.ab cd R R > B. ab cd R R < C. ab cd R R = D.无法确定三、计算题：1. 下图所示电路，用电源的等效变换化简电路（化成单个电压源和电阻的串联形式）。

(15V,2Ω)2．下图所示电路，用电源的等效变换化简电路（化成单个电流源和电阻并联的形式）。

(10A,2Ω)3. 下图所示的电路，试分析电压表的读数（设电压表内阻无穷大）。

(0V)4．下图所示电路中，试求图中所示方向的电流I 和电压U 。

(-5V,0.75A)24VΩ5．试用叠加定理求下图所示电路中的各支路电流1234I I I I 、、、。

(-1.4A,0.6A,-0.4A,1.6A)46. 下图所示电路中，已知16R =Ω，23R =Ω，33R =Ω， L 5R =Ω，S 2A I =，若要使L 3A I =，求S ?U = (72V)7. 下图所示的电路，已知U S =6V ，I S =2A ，R 1=3Ω，R 2=6Ω，R 3=2Ω， R 4=6Ω，用叠加原理求I 。

(-1A)U S8. 下图所示电路中，求（1）当开关S 断开时的电流I ；（2）求当开关S 闭合后的电流I 。

(0A,2A)9. 试用戴维宁定理求解下图中的U 。

(7V,1.5Ω,10V)LI10. 用戴维宁定理求下图所示电路中的U。

(3V,2.5Ω,-2V)1Ω1Ω11. 如下图所示的电路，用戴维宁定理求I。

(20V,2Ω,4A)ΩRLI12. 对于下图所示电路，已知U=2.5 V，试用戴维宁定理求解电阻R。

(8V,2.2Ω,1Ω)R1013. 试求下图所示电路的U。

(3.2V,3.2Ω,0V)14. 下图所示电路中，已知Rx 支路的电流为0.5A ，试求Rx 。

(3.5V,2.4Ω, 4.6Ω)R X0.5A15. 用叠加定理求下图所示电路中的I 。

(-4V,3Ω,4A)16. 用戴维宁定理求下图中5Ω电阻上的电压。

(-4V,5Ω,-2V)12Ω517.下图所示的电路，试用戴维宁定理求电流I 。

(12V,6.67Ω,12A)Ω6Ω18. 下图所示的电路，试用戴维宁定理求电流I 。

(15V,9Ω,1A)Ω5Ω19. 用结点电压法求下图所示电路中的各支路电流12,,I I I 。

(112.5V,28.125A,9.375A,8.75A)_1200.8Ω。