第二章 电路的分析方法
- 格式:doc
- 大小:664.00 KB
- 文档页数:20
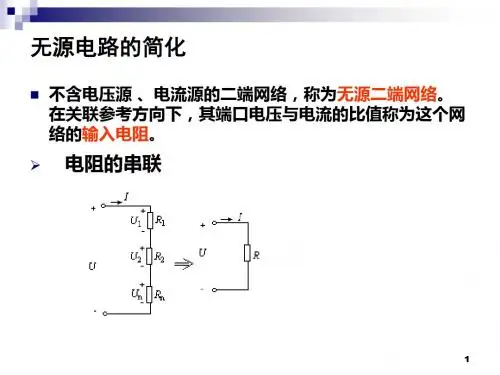

第二章电路的分析方法电路分析是指在已知电路构和元件参数的情况下,求出某些支路的电压、电流。
分析和计算电路可以应用欧姆定律和基尔霍夫定律,但往往由于电路复杂,计算手续十分繁琐。
为此,要根据电路的构特点去寻找分析和计算的简便方法。
2.1 支路电流法支路电流法是分析复杂电路的的基本方法。
它以各支路电流为待求的未知量,应用基尔霍夫定律(KCL 和KVL )和欧姆定律对结点、回路分别列出电流、电压方程,然后解出各支路电流。
下面通过具体实例说明支路电流法的求解规律。
例2-1】试用支路电流法求如图2-1 所示电路中各支路电流。
已知U S1 130V ,U S2 117V ,R1 1 ,R2 0.6 ,R 24 。
【解】该电路有3 条支路(b=3),2个结点(n=2),3 个回路(L=3 )。
先假定各支路电流的参考方向和回路的绕行方向如图所示。
因为有3 条支路则有3 个未知电流,需列出3 个独立方程,才能解得3个未知量。
根据KCL 分别对点A、B 列出的方程实际上是相同的,即结点A、B 中只有一个结点电流方程是独立的,因此对具有两个结点的电路,只能列出一个独立的KCL 方程。
再应用KVL 列回路电压方程,每一个方程中至少要包含一条未曾使用过的支路(即没有列过方程的支路)的电流或电压,因此只能列出两个独立的回路电压方程。
根据以上分析,可列出3 个独立方程如下:结点A I1 I2 I 0回路ⅠI1R1 I2R2 U S1 U S2回路ⅡI2 R2 IR U S2I1 10A, I2 5A, I=5A 联立以上3 个方程求解,代入数据解得支路电流通过以上实例可以总出支路电流法的解题步骤是:1.假定各支路电流的参考方向,若有n个点,根据KCL 列出(n-1)个结点电流方程。
2.若有b 条支路,根据KVL 列(b-n+1)个回路电压方程。
为了计算方便,通常选网孔作为回路。
5 3.解方程组,求出支路电流。
【例 2-2】如图 2-2 所示电路,用支路电流法求各支路电流。








第二章 电路的分析方法知识要点一、内容提要在任何一个直流电路中电阻的串并联最为常见,所以常用电阻的串并联等效变换的方法将一个电路化简为单回路电路,计算极为简单。
如果不能用电阻的串并联等效变换简化电路,可以根据不同的电路结构采用不同的分析方法如支路电流法、叠加原理、节点电位法、电源模型及其等效互换、等效电流定理等几种方法进行分析、计算。
二、基本要求1. 对支路电流法、支路电压法作一般了解。
2. 能正确理解叠加原理、戴微南定理、两源互换的适用条件。
3. 能熟练运用叠加原理、戴微南定理、两源互换计算复杂电路中的有关P 、U 、I 。
三、学习指导在电路诸多的分析方法中,支路法(电流法、电压法)最为基本,是直接应用克希荷夫两个定律列出联立方程求解;叠加原理和戴维南定理是重点,在本课程中常用到。
本章的难点是电流源和理想电流源,它比较生疏,不像电压源那样熟悉和具体,不易理解,所以在学习本章过程中应注意以下几点:1. 电阻的串联与并联(1)电阻串联:首尾依次相连,通过同一电流。
由欧姆定律可知总电阻为各电阻之和,即: ∑=iRR各电阻电压分配关系:s U RR U i i =,式中s U 为总电压。
(2)电阻并联:首首共端,尾尾共端,承受同一电压。
由欧姆定律可知总电阻为:∑=iR R 11各支路电流分配关系:s I R R I ii =,式中s I 为总电流。
并联电阻越多,则总电阻越小,电路中总电流和总功率就越大,但每个电阻的电流和功率却不变。
2. 电压源与电流源及其等效互换(1) 从电压源模型引出电流源模型,由图2-1(a)可知I R E U 0-=,两边除以0R 得I I I R E R U sc -=-=或 I R U I sc +=式中:0R E I sc =为电源的短路电流;I 为负载电流;R U 为引出的另一个电流(内阻的分流)。
于是上式可用图2-1(b)表示为电流源模型。
注意:①由电压源转为电流源时,其方向应保持为与电动势E 的方向相同。
②理想电压与理想电流源之间不存在等效互换关系。
③0R 不限于电源的负电阻,可以包括其它与电源相连而最后能简化为一个等效电阻0R 的全部电阻。
(2) 任何一个实际电源都可以等效为电压源或电流源的两种形式。
电压源和电流源其内部电路是不等效的, 只是对外部电路才是等效的,这反映在两电源的外特性是一致的,如图2-2所示。
注意:①理想电压源与理想电流源不能等效互换。
理想电压源和理想电流源实际上也并不存在,只是一种抽象模型,即当电压源内阻L 0R R 〈〈时,E U ≈,电压基本上恒定,所以才可近似认为是理想电压源;当电流源内阻L 0R R 〉〉时,0R E I ≈,电流基本上恒定,所以才可近似认为是理想电流源。
②两种电源模型对外电路等效关系不只限于内阻0R ,只要是一个电动势为E 的理想电压源和某个电阻R 串联的电路,都可能等效成一个电流源为sc I 的理想电流源和这个电阻并联的电路。
而R 可以是除理想电压源或理想电流源以外,能够用串并联方法等效而成的总电阻。
因此,利用二者的等效关系可以对电路进行化简,以便于分析和计算。
a(a)+ -U ⇒ a(b)+ -U 图2-1 由电压源模型转换为电流源模型3. 分析、计算电路的各种方法 (1) 支路电流法支路电流法是分析电路最基本的方法,具体方法为:①从所给电路图上找出支路b 节点n 各有多少,以支路电流为未知数,共需列出b 个方程;②在电路图上标出电压和电流的参考方向;③先用克希霍夫电流定律(KCL)对节点列出1-n 个独立方程;④再用克希霍夫电压定律(KVL)对回路列出其余)1(--n b 个独立方程。
支路电流法适合于支路数较少的电路,对于支路数较多的电路,由于所需方程较多,所以求解时有一定的麻烦。
(2) 叠加原理叠加原理是在有n 个电源的线性电路中,n 个电源共同作用时在某一支路中所产生的电流或电压,等于各个电源单独作用时分别在该支路中所产生的电流或电压的代数和。
叠加原理是关于各个电源作用的独立性原理,它是一种分析线性问题的普遍原理。
在电路的分析解题时,应按下列步骤进行。
①先将原电路图等效画成由各个独立源单独作用的分电路图。
画等分图时注意,将其中不作用的独立理想电压源短路,独立理想电流源开路,并在各分电路中标出支路电流或电压的参考方向,但独立电源的内阻及所有的受控源仍须保留,然后求解各支路电流(或电压)。
②将各分电路的支路电流(或电压)进行叠加,即得原电路中相关支路的电流(或电压)。
注意:①将各分量的参考方向(或参考极性)如与原电路中的相关量的参考方向(或参考极性)一致皆为正,相反者为负;②功率的计算不能用叠加原理,因为它不是线性方程。
(3) 节点的电位(电压)法节点电位(电压)法是先求出各节点的电位,再求出各支路的电流,此种方法特别适用于计算只有两个节点的电路。
以两节点电路为例,导出节点电位(电压)公式 :∑∑=RR E V 1/)( 其中∑RE有正负号之分。
当电动势E 和节点电位(电压)U 的参考方向相同时取正号,相反时则取负号,而与各支路电流的参考方向无关。
∑R1的各项均为正值,如果电路中有三个U =0Isc(a)00R I U sc =Isc (b)图2-2 电压源和电流源的外特性节点,可设其中一个节点的电位为零,而后计算其余节点的电位,即节点与零电位节点间的电压。
其步骤和两节点电路是一样的。
(4) 等效电源定理在一个电路中,如果只需计算某条支路的电压或电流时,可将此支路以外的其余部分看做有源两端网络,并用等效电源定理之一的戴维南定理简化成等效电压源或用等效电源定理之二的诺顿定理化成等效电流源,然后再进行计算。
分析简化过程中注意下列几点。
①将待求支路中的x R 从电路中断开,求出其它剩下的有源两端网络的开路电压0U ,即为戴维南等效电路中的电压的电动势;求出有源两端网络的短路电流SC I ,即为诺顿等效电路中电流源的电激流。
②将有源两端网络的电源除去(理想电压源短路,理想电流源开路),保留其内阻,然后求出该无源两端网络的等效电阻0R ,即为等效电源的电阻。
③将待求支路X R 接入以0U 为电压源,串联内阻为0R 的等效电阻,如图2-3所示。
然后由全电路欧姆定律可以求得待求支路电流为0X 0R R U I +=,待求支路电压为:00IR U U -=④将待求支路x R 接入短路电流为SC I 、并联内阻为0R 的等效电流源如图2-4所示,则待求支路的电流、电压分别为:SC 0X 0I R R R I +=,X IR U =⑤对于较为复杂的电路,有时 还可以利用电压源与电流源的等效互换,结合使用戴维南定理和诺顿定理对电路进行化简再计算。
(5)受控电源电路含受控电源电路的分析,要了解四种理想受控电源的模型,即:与压控电源(VCVS )、流控电压源(CCVS )压控电流源(VCCS )、流控电流源(CCCS );同时应对相应受控源中的系数βγμ、、及g 的意义要有所理解。
对于含有受控源的线性电路,原则上可采取上述电路的分析方法进行分析计算,但常考虑其特性和具体情况,比如:用叠加原理解题时,分解后的电路中均应保持受控电源的作用。
a图2-3 戴维南等效电路+ -U a+ -U 图2-4 诺顿等效电路(6)非线性电阻电路的计算对于简单非线性电阻电路的分析与计算一般可按下述几步进行: ①将电路的线性部分和非线性部分区分开;②列出线性部分的电压方程,必要时需先进行化简;③在非线性元件的伏安特性曲线上,画出线性元件的特性曲线(即电压方程所表示的直线);④由两条特性曲线的交点Q (称之为工作点)来确定电路的工作状态。
注意:(5)、(6)两点做本章选学内容。
P39 习题二2-1 已知如图,Ω=Ω=Ω=Ω=Ω==1,3,4,3,6,V 6E 54321R R R R R试求 43I I 和题2-1图 题2-1等效图 解:334424144I R R I R I RR I ⋅=⋅+⎪⎪⎭⎫ ⎝⎛+⋅ ① 33341445I R E I I R R I R ⋅-=⎥⎦⎤⎢⎣⎡++ ② 344443363I I I I =+⎪⎭⎫⎝⎛+,344215I I = 34815I I = ①33444621I I I I -=⎪⎭⎫⎝⎛++,345623I I -= 3410123I I -=,34506015I I -=,A 2930,302933==I I代入 ①A 2916,293081544=⨯=⨯I I另外,戴维南等效图A 29549296I 5==回归原图 3355I R I R E ⋅=⋅-,所以 A 293042954163=⨯-=I2-2 电阻4321R R R R ===并联接在220V 的直流电源上,共消耗功率400W 。
如把4个电阻改成串联,接在原电源上,试问:此时电源的负载是增大了?还是减小了?两种情况下,电源输出的功率各为多少? 答 由并联输出功率400w 所以每个R 获得功率RUP 2,W 1004400==)(484,2201002Ω==R R改串联后:W 25422220P P 222=⨯===总消耗输出R U2-3 电路如图所示,计算a 、b 两点间的等效电阻。
题2-3 图题2-3等效图 Ω=++⨯=++⋅=313212123121112111R R R R R R ,Ω=++⨯=++⨯=13213223121123122R R R R R RΩ=++⨯=++⋅=213213123121123133R R R R R R)(913910312953125225231ab Ω=+=+=+⨯+=R 2-4 电路如图所示,等效变换为星型联接,3个等效电阻各为多少?设图中各电阻均为R 。
题2-4图1Ωa2题2-4 △-Y 变换(一)图题2-4 △-Y 变换(二)图bcbc题2-4 △-Y 变换(三)图题2-4 等效星型图2-5 电路如图所示,将电压(电流)源等效互换成电流(电压)源。
图中电阻、电压源、电流源单位分别为Ω、V 、A 。
解:cc题2-5 (a)图题2-5 (c )图题2-5 (b )图2-6 用两种电源等效互换的方法,求电路中5Ω电阻上消耗的功率。
习题2-6图解:由两源互换,原图可变为下图A 194215=--,所以:W 551252=⨯=⋅=R IP2-7 试用支路电流法和节点电压法求如图所示各支路的电流,并求4Ω电阻上消耗的功率。
题2-5 (d )图Ω2题2-7 图解:① II I I I I I 44.011648.0120102121=-=-=++ II II II I 102905150102121=-=-=++I I I 15)(44021=+-,I 16450=A 8225A 16450==I1622501501=-I所以 :A 875A 1615016225024001==-=I164500292=-IA 435161401645004640164500401162==-=-⨯=I② isg i R I R E U 12∑∑+∑=V 2225418.0310290150414.018.01104.01168.0120=+++=++++=U所以:A 8225414450=⨯==R U I W 31641622548225222R ≈=⨯⎪⎭⎫⎝⎛==R I P2-8 试用支路电流法和节点电压法求如图所示各支路的电流。