层次分析法判断矩阵求权值以及一致性检验程序(20210228092109)

层次分析法判断矩阵求权值以及一致性检验程序层次分析法（Analytic Hierarchy Process，AHP）是一种用于多准则决策的数学模型和方法。

它是由美国管理学家托马斯·L·赛蒙在20世纪70年代提出的。

AHP方法能够帮助决策者在多个准则和多个选择之间进行有效的决策，通过定量和定性的方式来对选择进行评估和比较。

在AHP方法中，决策问题被分解成一个层次结构，其中包含目标层、准则层和选择层。

每个层次都有不同的准则和可能的选择。

决策者需要对每个层次中的准则和选择进行配对比较，从而确定它们之间的重要性和权重。

通过对一系列两两比较的判断矩阵求权值，最终得到每个准则和选择的权重，进而做出最终决策。

下面是一种求解AHP中矩阵权值和进行一致性检验的程序：1. 建立判断矩阵：根据决策问题的结构，建立一个判断矩阵。

判断矩阵的大小是n×n，其中n是比较对象的数量。

矩阵的每个元素(a_ij)表示第i个对象相对于第j个对象的重要性或影响程度。

2. 进行两两比较：对矩阵的每个元素(a_ij)，决策者需要进行两两比较，确定它们之间的相对重要性。

比较的结果可以使用系数1-9进行量化，其中1表示相等重要性，9表示绝对重要性的差异。

3.归一化判断矩阵：将比较得到的判断矩阵归一化，使得每一列的元素之和等于1、这可以通过将每个元素除以其所在列的元素之和来实现。

4.求解权值：通过归一化后的判断矩阵，可以计算每个对象的权重。

权重可以通过计算每一行的元素之和来得到。

5.计算一致性指标：在AHP方法中，一致性是指判断矩阵中的数值是否在合理范围内。

为了检验一致性，需要计算一致性指标。

一致性指标的计算方法是通过求解最大特征值和一致性比率来得到。

6.进行一致性检验：计算一致性指标后，需要将其与预先给定的随机一致性指标进行比较。

如果计算得到的一致性指标小于预先给定的一致性指标，则认为判断矩阵中的数值具有一致性。

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。

其中A为判断矩阵，不同的标度和评定A将不同。

m为A的维数RI为判断矩阵的平均随机一致性指标：根据m的不同值不同。

当CR<0.1时符合一致性检验，判断矩阵构造合理。

下面是层次分析法的简介，以及判断矩阵构造方法。

一.层次分析法的含义层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.Saaty）正式提出。

它是一种定性和定量相结合的、系统化、层次化的分析方法。

由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。

它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。

（1）层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。

层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

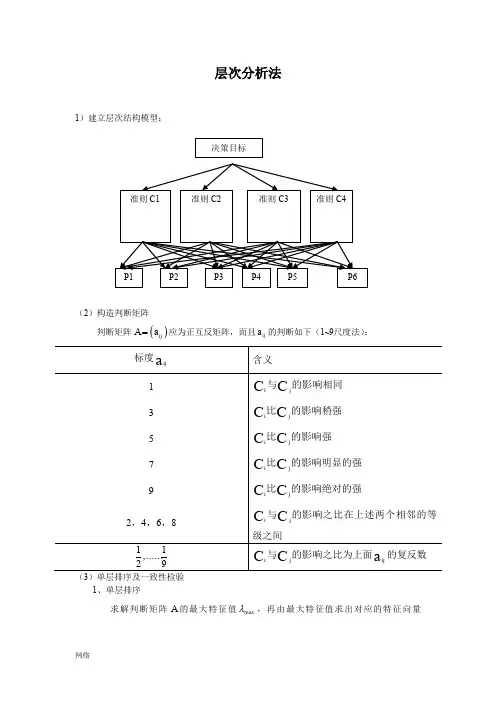
层次分析法1）建立层次结构模型：（2）构造判断矩阵判断矩阵()ij A a =应为正互反矩阵，而且ij a 的判断如下（1~9尺度法）：（3）单层排序及一致性检验1、单层排序求解判断矩阵A 的最大特征值max λ，再由最大特征值求出对应的特征向量ω()max A ωλω=，并将ω标准化，即为同一层相对于上一层某一因素的权重，根据此权重的大小，便可确定该层因素的排序。

2、一致性检验取一致性指标max 1nCI n λ-=-，（n 为A 的阶数）令CR RI=，若0.1CR <，则认为A 具有一致性。

否则，需要对A 进行调整，直到具有满意的一致性为止。

（4）层次总排序及一致性检验假定准则层12,,,n C C C 排序完成，其权重分别为12,,,n a a a ，方案层P 包含m 个方案：12,,,m P P P 。

其相对于上一层的()1,2,,j C j n =对方案层P 中的m 个方案进行单层排序，其排序权重记为12,,,j j mj b b b ()1,2,,j n =，则方案层P 中第i 个方案Pi 的总排序权重为1nj ijj a b=∑，见下表：从而确定层的排序。

例：纯文本文件txt3.txt 中的数据格式如下：1 1 1 4 1 1/2 1 1 2 4 1 1/2 1 1/2 1 53 1/2 1/4 1/4 1/5 1 1/3 1/3 1 1 1/3 3 1 12 2 23 3 11 1/4 1/24 1 32 1/3 11 1/4 1/54 1 1/25 2 11 3 1/31/3 1 1/73 7 11 1/3 53 1 71/5 1/7 11 1 71 1 71/7 1/7 11 7 91/7 1 11/9 1 1matlab程序：>> fid=fopen('txt3.txt','r');n1=6;n2=3;a=[];for i=1:n1tmp=str2num(fgetl(fid));a=[a;tmp]; %读准则层判断矩阵endfor i=1:n1str1=char(['b',int2str(i),'=[];']);str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); eval(str1);for j=1:n2tmp=str2num(fgetl(fid));eval(str2); %读方案层的判断矩阵endendri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标[x,y]=eig(a);lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));cr0=(lamda-n1)/(n1-1)/ri(n1)for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num));cr1(i)=(lamda-n2)/(n2-1)/ri(n2);endcr1, ts=w1*w0, cr=cr1*w0层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法层次分析法实例与步骤结合一个具体例子，说明层次分析法的基本步骤和要点。

层次分析法流程图
层次分析法，是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

以下是店铺为大家整理的关于层次分析法流程图，给大家作为参考，欢迎阅读! 层次分析法流程图
AHP层次分析法的步骤和方法
1.建立层次结构模型
将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

2.构造判断矩阵
在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty等人提出：一致矩阵法，即：不把所有因素放在一起比较，而是两两相互比较。

对比时采用相对尺度，以尽可能减少性质不同因素相互比较的困难，以提高准确度。

3.层次单排序
所谓层次单排序是指，对于上一层某因素而言，本层次各因素的重要性的排序。

4.判断矩阵的一致性检验
所谓一致性是指判断思维的逻辑一致性。

如当甲比丙是强烈重要，而乙比丙是稍微重要时，显然甲一定比乙重要。

这就是判断思维的逻辑一致性，否则判断就会有矛盾。

5.层次总排序
确定某层所有因素对于总目标相对重要性的排序权值过程，称为层次总排序。

这一过程是从最高层到最底层依次进行的。

对于最高层而言，其层次单排序的结果也就是总排序的结果。

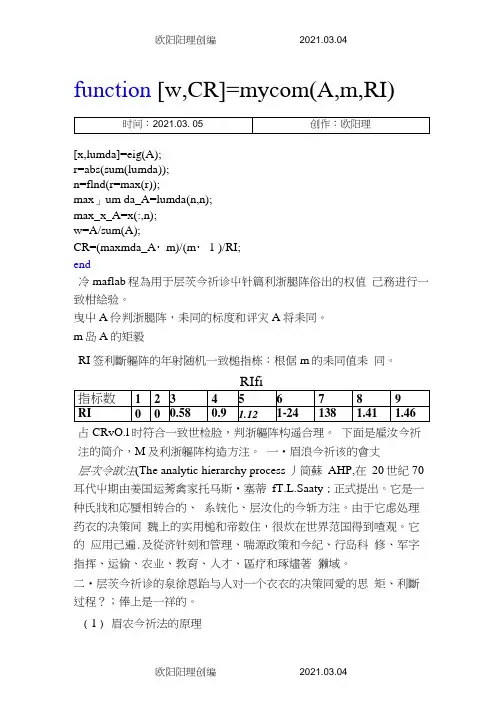
function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=flnd(r=max(r));max」um da_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(maxmda_A・m)/(m・ 1 )/RI;end冷maflab程為用于层茨今祈诊屮针篇利浙腿阵俗出的权值己務进行一致柑絵验。

曳屮A伶判浙腿阵，耒同的标度和评灾A将耒同。

m岛A的矩毅RI签利斷軀阵的年射随机一致槌指栋：根倨m的耒同值耒同。

占CRvO.l时符合一致世检脸，判浙軀阵构遥合理。

下面是雇汝今祈注的简介，M及利浙軀阵构造方注。

一•眉浪今祈该的會丈层次令歆注(The analytic hierarchy process 丿简蘇AHP,在20世紀70耳代屮期由姜国运莠禽家托马斯•塞蒂fT.L.Saaty；正式提出。

它是一种氏戕和応蜃相转合的、系铳化、层汝化的今斩方注。

由于它虑处理药衣的决策间魏上的实用槌和帝数住，很炊在世界范国得到喳观。

它的应用己遍.及從济针刻和管理、喘源政策和今紀、行岛科修、军字指挥、运偷、农业、教育、人才、區疗和琢燼著獭域。

二•层茨今祈诊的泉徐恩跆与人对一个衣衣的决策同愛的思矩、利斷过程？；俸上是一祥的。

（1）眉农今祈法的原理层浪今祈注是将决策同舉按总目标、各眉&目标、评价帝则直至其体的备按方案的顺潯今解怎耒同的层茨秸构，& 后得用求解判瞬腿阵持征向蜃的办法，求得毎一层次的各无素对上一层茨某免索的优老权重，舉后再加权和的方注遗阶归弄各备挥方案对总同标的舉终权重，此眾終权重儼农老即岛儼优方案。

这里所谓“优老权重"是一种相对的蜃凌，它热鋼各备挥方案虚某一特支的评价帝则或&貝标，标下优越程度的相对蜃及，以及各&同标对上一雇目标而咅唾要程及的相对蜃度。

雇茨今祈法比轶适合于其痛今眉•金错评价指标的目标系俛，而且貝标值乂珞于底蜃描述的决策间魏。

层次分析法的基本原理和步骤层次分析法（Analytic Hierarchy Process, AHP）是一种定量分析方法，用于多准则决策问题的分析和决策。

它的基本原理是将复杂的决策问题层次化，通过对准则和方案的比较与评价，得出优先级权重，进而得到最佳方案。

1.确定决策目标：确定决策问题的目标，明确要达到的结果。

2.构建层次结构：将决策问题分解成一个层次结构，包括目标层、准则层和方案层。

目标层表示最终要达到的目标，准则层表示影响目标实现的准则因素，方案层表示可供选择的决策方案。

3.构建判断矩阵：在准则层和方案层中，两两比较各个准则或方案之间的重要性或优劣程度。

根据专家判断或个人主观意见，使用尺度（1-9）对两两比较进行评分，构建判断矩阵。

4.计算准则权重：根据判断矩阵的评分，使用特征值法或最大特征向量法计算准则权重。

首先对判断矩阵的列向量进行归一化处理，然后计算归一化后的特征向量，最后将特征向量的元素相加，并按比例得到准则的权重。

5.一致性检验：通过计算一致性指标和一致性比率来检验判断矩阵的一致性。

一致性指标表示判断矩阵与一致性判断矩阵之间的差异程度，一致性比率表示判断矩阵的一致性程度。

如果一致性指标小于一定阈值，且一致性比率接近1，则认为判断矩阵具有满足一致性的权重。

6.计算方案权重：将计算得到的准则权重与判断矩阵相乘，计算每个方案的权重。

权重值越大，表示方案的优先级越高。

7.一致性检验：对方案权重进行一致性检验，与准则权重的一致性检验类似。

8.敏感性分析：通过增加或减少一些因素的权重，分析结果的稳定性和可靠性。

敏感性分析可以帮助决策者了解权重对决策结果的影响程度。

9.最终决策：根据方案的权重和准则的权重，对各个方案的优先级进行排序，选择权重最高的方案作为最终决策。

层次分析法的基本原理是将决策问题逐层分解，通过两两比较和权重计算，理性地确定各个因素的优先级和权重。

通过分析和评价不同方案，辅助决策者做出最佳选择。

先确定判断矩阵；然后用以下程序就好了：%层次分析法的matlab程序%%%%diertimoxingyiclc,cleardisp('输入判断矩阵');% 在屏幕显示这句话A=input('A=');% 从屏幕接收判断矩阵[n,n]=size(A);% 计算A的维度，这里是方阵，这么写不太好x=ones(n,100);% x为n行100列全1的矩阵y=ones(n,100);% y同xm=zeros(1,100);% m为1行100列全0的向量m(1)=max(x(:,1));% x第一列中最大的值赋给m的第一个分量y(:,1)=x(:,1);% x的第一列赋予y的第一列x(:,2)=A*y(:,1);% x的第二列为矩阵A*y(:,1)m(2)=max(x(:,2));% x第二列中最大的值赋给m的第二个分量y(:,2)=x(:,2)/m(2);% x的第二列除以m(2)后赋给y的第二列p=0.0001;i=2;k=abs(m(2)-m(1));% 初始化p，i，k为m(2)-m(1)的绝对值while k>p% 当k>p是执行循环体i=i+1;% i自加1x(:,i)=A*y(:,i-1);% x的第i列等于A*y的第i-1列m(i)=max(x(:,i));% m的第i个分量等于x第i列中最大的值y(:,i)=x(:,i)/m(i);% y的第i列等于x的第i列除以m的第i个分量k=abs(m(i)-m(i-1));% k等于m(i)-m(i-1)的绝对值enda=sum(y(:,i));% y的第i列的和赋予aw=y(:,i)/a;% y的第i列除以at=m(i);% m的第i个分量赋给tdisp('权向量:');disp(w);% 显示权向量wdisp('最大特征值:');disp(t);% 显示最大特征值t%以下是一致性检验CI=(t-n)/(n-1);% t-维度再除以维度-1的值赋给CIRI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准CR=CI/RI(n);% 计算一致性if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);elsedisp('此矩阵的一致性不可以接受!'); end。

层次分析法（Analytic Hierarchy Process，简称AHP）是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。

它是美国运筹学家T. L. Saaty 教授于70 年代初期提出的一种简便、灵活而又实用的多准则决策方法。

§1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。

层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

运用层次分析法建模，大体上可按下面四个步骤进行：（i）建立递阶层次结构模型；（ii）构造出各层次中的所有判断矩阵；（iii）层次单排序及一致性检验；（iv）层次总排序及一致性检验。

下面分别说明这四个步骤的实现过程。

1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。

在这个模型下，复杂问题被分解为元素的组成部分。

这些元素又按其属性及关系形成若干层次。

上一层次的元素作为准则对下一层次有关元素起支配作用。

这些层次可以分为三类：（i）最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。

（ii）中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。

（iii）最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地层次数不受限制。

每一层次中各元素所支配的元素一般不要超过9 个。

这是因为支配的元素过多会给两两比较判断带来困难。

下面结合一个实例来说明递阶层次结构的建立。

例1 假期旅游有、、3 个旅游胜地供你选择，试确定一个最佳地点。