构造判断矩阵的讲解(层次分析法)..
- 格式:ppt
- 大小:294.00 KB
- 文档页数:19



二、AHP 求解层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法, 将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:c 1自然属性、c 2经济价值、C 3基础设施、c 5政府政策。
方案层:设三个方案分别为:A i 农产品产地一产地批发市场一销地批发市场一消费者、A 2农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、A 3农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区 )。
A 3图3— 1递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵是以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为目标层:G :最优生鲜农产品流通模式准则层:自然属性经济价值基础设施政府政策方案层:了使各因素之间进行两两比较得到量化的判断矩阵,弓I入1〜9的标度,见表3—1.为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根入max的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
由于入连续的依赖于a ij,则入比n大的越多,A 的不一致性越严重。
用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用入一n数值的大小来衡量A的不一致程度。
用一致性指标进行检验:CImax nCRCI RI用一致性指标进行检验:CI 工 n。

1. 层次分析法(The analytic hierarchy process, 简称AHP)用于解决评价类问题,例如:选择那种方案最好、哪位运动员或者员工表现的更优秀。
评价类问题可以用打分解决。
层次分析法 (The Analytic Hierarchy Process即 AHP)是由美国运筹学家、匹兹堡大学教授T. L. Saaty于20世纪70年代创立的一种系统分析与决策的综合评价方法, 是在充分研究了人类思维过程的基础上提出来的, 它较合理地解决了定性问题定量化的处理过程。
AHP的主要特点是通过建立递阶层次结构, 把人类的判断转化到若干因素两两之间重要度的比较上, 从而把难于量化的定性判断转化为可操作的重要度的比较上面。
在许多情况下, 决策者可以直接使用AHP进行决策, 极大地提高了决策的有效性、可靠性和可行性, 但其本质是一种思维方式, 它把复杂问题分解成多个组成因素, 又将这些因素按支配关系分别形成递阶层次结构, 通过两两比较的方法确定决策方案相对重要度的总排序。
整个过程体现了人类决策思维的基本特征,即分解、判断、综合,克服了其他方法回避决策者主观判断的缺点。
1.1模型介绍1.1.1引例高考结束了,小明该选择华科还是五武大?小明最关心四个方面:学习氛围0.4、就业前景0.3、男女比例0.2、校园景色0.19(权重和为1)(1)学习氛围:经查阅资料查到“学在华工,玩在武大,爱在华师”一句话,因此在学习氛围方面给华科0.7,给武汉大学0.3.(2)就业前景:搜索两所学校就业率差不多,因此在就业前景方面对两所学校均赋予0.5的权重。
(3)男女比例:经查询,华科男女比例2:1,武大1.35:1,因此武大0.7分,华科0.3分(4)校园景色:华科0.25分,武大0.75分整理权重表格:指标权重华科武大学习氛围0.40.70.3就业前景0.30.50.5男女比例0.20.30.7校园景色0.10.250.75华科最终的得分:0.7*0.4+0.5*0.3+0.3*0.2+0.25+*0.1=0.515分武大最终得分:0.3*0.4+0.5*0.3+0.7*0.2+0.75*0.1=0.485分1.1.2 模型1、关键词:打分法、确定评价指标、形成评价体系2、解决评价类问题,首先确定以下三个问题:(1)评价的目标是什么(2)为了达到这个目标有哪几种可选的方案(3)评价的准则或者说指标是什么(我们根据什么东西来评价好坏)。

构造判断矩阵的讲解层次分析法(Analytic Hierarchy Process,简称AHP)是一种用于处理决策问题的定量方法。
它通过将问题分解为一系列相互关联的准则和备选方案,并使用判断矩阵来定量评估它们之间的相对重要程度,从而帮助决策者进行决策。
一、构造判断矩阵的基本思想判断矩阵是用于量化准则和备选方案之间相对重要程度的工具。
构造判断矩阵的基本思想是通过比较两个元素之间的重要程度,将其转化为一个数值。
这个数值被称为重要性权重。
二、判断矩阵的构建过程1.确定准则和备选方案:首先,需要明确决策问题的准则和备选方案。
准则是衡量备选方案优劣的标准,备选方案是实施决策的可行选择。
2.构建层次结构:将准则和备选方案按照层次结构组织起来。
层次结构由若干层次组成,最顶层是目标层次,下一层是准则层次,最底层是备选方案层次。
3.定义判断矩阵:对于每一对元素,决策者根据其重要程度来填写判断矩阵的元素。
判断矩阵是一个n×n的矩阵,其中n是准则或备选方案的个数。
4.判断矩阵的填写:对于准则层次的判断矩阵,决策者评价不同准则之间的相对重要程度,从1到9进行评分,其中1表示两个准则同等重要,9表示一个准则远远重要于另一个准则。
对于备选方案层次的判断矩阵,决策者评价不同备选方案之间的相对重要程度。
5.判断矩阵的一致性检验:进行一致性检验是为了保证判断矩阵的可靠性。
通过计算判断矩阵的最大特征值和一致性指标,确定判断矩阵是否通过一致性检验。
三、判断矩阵的数学原理判断矩阵是根据相对重要程度进行填写的。
根据AHP的原理,假设第i个准则对于第j个准则的相对重要程度为A(i,j),那么相对重要程度满足以下两个条件:1.A(i,j)=1/A(j,i):即准则i相对于准则j的重要程度与准则j相对于准则i的重要程度互为倒数。
2.A(i,j)×A(j,k)=A(i,k):即准则i相对于准则j的重要程度与准则j相对于准则k的重要程度的乘积等于准则i相对于准则k的重要程度。


层次分析法—规划决策的工具随着社会的快速发展和全球化进程的加速,越来越多的组织和决策者面临着复杂多变的挑战。
在这个背景下,层次分析法(Analytic Hierarchy Process,AHP)作为一种系统化的决策工具,开始受到广泛。
本文将详细介绍层次分析法及其在规划决策中的应用。
规划决策是指根据组织的目标和资源,制定出一套具体的行动方案。
规划决策需要综合考虑各种因素,如政策、经济、社会和环境等。
在这个过程中,层次分析法能够将复杂的问题分解为多个层次,帮助决策者更加清晰地认识问题,从而做出更加科学、合理的决策。
层次分析法是一种结构化、系统化的决策方法,其核心是将一个复杂的问题分解为多个层次,如目标层、准则层和方案层等。
每个层次上的元素通过相互比较,确定其相对重要性,然后根据一致性检验进行排序。
根据每个元素的权重,得出方案层的优劣排序,为决策者提供依据。
层次分析法在规划决策中具有广泛的应用。
例如,在制定城市发展规划时,可以将城市的经济、社会和环境目标作为目标层,将不同的规划方案作为方案层,然后通过层次分析法对方案进行评估和排序。
在选择合作伙伴、制定军事策略等领域,层次分析法也发挥了重要作用。
与其他规划决策方法相比,层次分析法具有以下优点:系统性:层次分析法将问题分解为多个层次,使决策过程更加系统化、条理清晰。
定量性:层次分析法通过比较元素之间的相对重要性,并计算各元素的权重,使决策过程更加定量、精确。
可比性:层次分析法采用一致性检验对元素进行排序,保证不同方案之间的可比性。
虽然层次分析法在规划决策中具有许多优点,但也存在一些不足:主观性:层次分析法中的判断和权重分配往往基于专家或决策者的主观意见,这可能导致结果具有一定的主观性和片面性。
适用范围有限:层次分析法适用于多准则、多目标的问题,但对于某些复杂问题可能无法完全适用。
计算复杂度较高:层次分析法的计算过程可能较为复杂,尤其是当问题涉及的元素较多时,需要消耗大量计算资源。



层次分析法中判断矩阵的构造问题作者:储敏学位授予单位:南京理工大学1.参考文献2.郭亚军综合评价理论与方法 20023.秦寿康综合评价原理及应用 20034.王雪华两种层次结构化决策方法的理论与应用研究--AHP与AIM 20005.王莲芬.许树柏层次分析法引论 19906.Saaty T L The Analytic Hierarchy Process 1980ler G A The magical number seven,plus or minus two:Some limits on our capacity for processing information 19568.左军层次分析法中判断矩阵的间接给出法 1988(10)9.徐泽水层次分析法中构造判断矩阵的新方法 1997(zk)10.徐泽水层次分析法新标度法 1998(10)11.舒康.梁镇伟AHP中的指数标度 1990(01)12.汪浩.马达层次分析法标度评价与新标度方法 1993(05)13.侯岳衡.沈德家指数标度及其与几种标度的比较[期刊论文]-系统工程理论与实践 1995(10)14.P J M Van Laarhoven.W Pedrycz A Fuzzy Extension of Saaty's Priority Theory 1983(03)15.许若宁.翟晓燕层次分析法中Fuzzy判断矩阵的建立及其排序 1988(05)16.王绪柱.刘进生.魏毅强模糊判断矩阵的一致性及权重排序 1995(01)17.诸克军.张新兰.肖荔瑾FuzzyAHP方法及应用[期刊论文]-系统工程理论与实践 1997(12)18.曹纯模糊AHP中权重向量的一种新算法[期刊论文]-西北民族学院学报(自然科学版) 1999(1)19.James J Buckley.Thomas Feuring.Yoichi Hayashi Fuzzy hierarchical analysis revisited 200120.Ruoning Xu Fuzzy least-squares priority method in the analytic hierarchy process 200021.许若宁Fuzzy判断矩阵的一致性修正[期刊论文]-数学研究与评论 2003(1)22.刘进生.魏毅强.王绪柱区间数判断矩阵的建立及其权重计算 1993(03)23.魏毅强.刘进生.王绪柱不确定型AHP中判断矩阵的一致性概念及权重[期刊论文]-系统工程理论与实践 1994(4)24.张吉军区间数的排序方法研究[期刊论文]-运筹与管理 2003(3)25.穆增超.郭小宣区间判断矩阵的一种新的排序方法[期刊论文]-汉中师范学院学报 2003(3)26.高洁.盛昭瀚可拓层次分析法研究[期刊论文]-系统工程 2002(5)27.骆正清关于层次分析法中判断矩阵间接给出法的讨论 1993(03)28.骆正清.杨善林层次分析法中几种标度的比较[期刊论文]-系统工程理论与实践 2004(9)29.徐泽水关于层次分析中几种标度的模拟评估[期刊论文]-系统工程理论与实践 2000(7)30.Malcolm Beynon An analysis of priority values from alternative comparison scales within AHP 200231.骆正清层次分析法中判断矩阵构造的新方法[期刊论文]-电子科技大学学报 1999(5)32.赵玮.岳德权AHP的算法及其比较分析 1995(01)33.章志敏.赵继超层次分析的广义梯度特征向量法[期刊论文]-经济数学 2000(4)34.王应明.徐南荣优化理论在层次分析法中的应用 1991(02)35.柴巧珠层次分析法的改进最小二乘排序法 1993(03)36.陈宝谦层次分析的两种新排序方法 1990(02)37.金菊良.魏一鸣.付强.丁晶计算层次分析法中排序权值的加速遗传算法[期刊论文]-系统工程理论与实践 2002(11)38.雷功炎关于将相对熵用于层次分析的简单注记 1995(03)39.E U choo.W C Wedley A common framework for deriving preference values from pairwise comparison matrices 200440.Chiclana F.Herrera F.Herrera-Viedma E Integrating three representation models in fuzzy multipurpose decision makingbased on fuzzy preference relation 199841.Tanino T Fuzzy preference orderings in group decision making 198442.陈守煜系统模糊决策理论与应用 199443.徐泽水模糊互补判断矩阵排序的一种算法[期刊论文]-系统工程学报 2001(4)44.樊治平.姜艳萍.肖四汉模糊判断矩阵的一致性及其性质[期刊论文]-控制与决策 2001(1)45.肖四汉.樊治平.王梦光Fuzzy判断矩阵的一致性研究[期刊论文]-系统工程学报 2001(2)46.樊治平.胡国奋模糊判断矩阵一致性逼近及排序方法[期刊论文]-运筹与管理 2000(3)47.姜艳萍.樊治平基于模糊判断矩阵的一种方案排序方法[期刊论文]-东北大学学报(自然科学版) 2000(4)48.肖四汉具有不同形式偏好信息的群决策理论与方法研究 200149.姜艳萍.樊治平一种用于模糊判断矩阵排序的χ2方法[期刊论文]-东北大学学报(自然科学版) 2000(5)50.樊治平.李洪燕.胡国奋一类Fuzzy判断矩阵及方案排序的目标规划方法[期刊论文]-东北大学学报 2000(1)51.徐泽水互补判断矩阵的两种排序方法--权的最小平方法及特征向量法[期刊论文]-系统工程理论与实践 2002(7)52.Jiang Y P.Fan Z P.Wang X R A lagrange multiplier ranking method for the fuzzy judgement matrix 200153.孔松泉.达庆利.徐泽水互补判断矩阵排序的广义χ2法[期刊论文]-东南大学学报(自然科学版) 2002(4)54.韦振中致判断矩阵与一致模糊矩阵的关系[期刊论文]-广西民族学院学报(自然科学版) 2001(2)55.宋光兴.杨德礼模糊判断矩阵排序向量的确定方法研究[期刊论文]-模糊系统与数学 2004(2)56.Y H Chen.Wen-june Wang.Chih-Hui Chiu New estimation method for the membership values in Fuzzy sets 20001.期刊论文骆正清.杨善林层次分析法中几种标度的比较-系统工程理论与实践2004,24(9)提出了用保序性、一致性、标度均匀性、标度可记忆性、标度可感知性、标度权重拟合性等标准,综合评价层次分析法中的不同标度;并用上述标准对现有的几种标度进行了比较,结论是:对单一准则下的排序,各种标度法都具有保序性,因而建议使用1~9标度;对精度要求较高的多准则下的排序问题,建议使用指数标度e0/5~e8/5 或e0/4~e8/4.2.学位论文占济舟关于层次分析法中标度问题的研究2005层次分析法(AHP)是由美国运筹学家,匹兹堡大学T.L.Saaty教授于20世纪70年代中期提出的,一种将决策者的定性判断和定量分析相结合的科学决策方法。
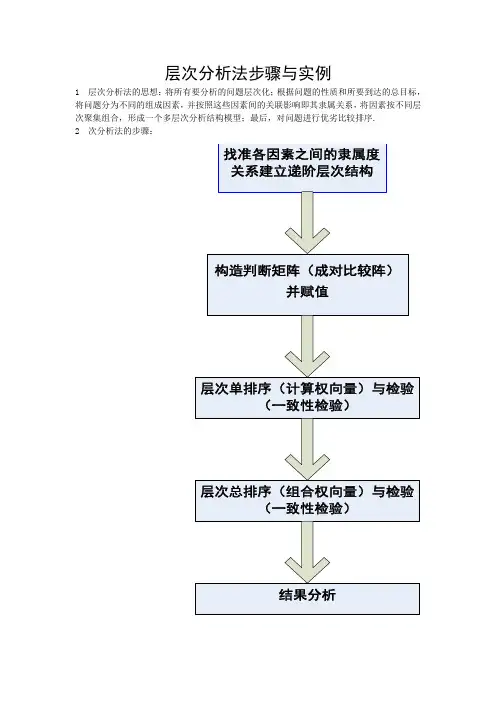
层次分析法步骤与实例1 层次分析法的思想:将所有要分析的问题层次化;根据问题的性质和所要到达的总目标,将问题分为不同的组成因素,并按照这些因素间的关联影响即其隶属关系,将因素按不同层次聚集组合,形成一个多层次分析结构模型;最后,对问题进行优劣比较排序.2 次分析法的步骤:3 以一个具体案例进行说明:【案例分析】市政工程项目建设决策:层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。
除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
【案例分析】市政工程项目进行决策:建立递阶层次结构 在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合效益最高,即决策目标是“合理建设市政工程,使综合效益最高”。
为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
但问题绝不这么简单。
通过深入思考,决策人员认为还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
假设本问题只考虑这些准则,接下来需要明确为了实现决策目标、在上述准则下可以有哪些方案。
根据题中所述,本问题有两个解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
很明显,这两个方案于所有准则都相关。
将各个层次的因素按其上下关系摆放好位置,并将它们之间的关系用连线连接起来。
同时,为了方便后面的定量表示,一般从上到下用A 、B 、C 、D 。
代表不同层次,同一层次从左到右用1、2、3、4。
代表不同因素。
这样构成的递阶层次结构如下图。
目标层A准则层B准则层C措施层D图1 递阶层次结构示意图2.构造判断矩阵(成对比较阵)并赋值根据递阶层次结构就能很容易地构造判断矩阵。
二、AHP 求解层次分析法(Analytic Hierarchy Process )是一种定量与定性相结合的多目标决策分析法,将决策者的经验给予量化,这在对目标(因素)结构复杂且缺乏必要数据的情况下较为实用。
(一)、建立递阶层次结构目标层:最优生鲜农产品流通模式。
准则层:方案的影响因素有:1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层:设三个方案分别为:1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构(二)、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵,引入1~9的标度,见表3—1.目标层:准则层:方案层:表3—1 标度值为了构造判断矩阵,作者对6个专家进行了咨询,根据专家和作者的经验,四个准则下的两两比较矩阵分别为:(三)、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素,排出评比的次序,这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
a,则λ比n 大的越多,A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验:max 1nCI n λ-=-。
其中max λ是比较矩阵的最大特征值,n 是比较矩阵的阶数。
层次分析法判断矩阵层次分析法判断矩阵程序先确定判断矩阵;然后用以下程序就好了:%层次分析法的matlab程序%%%%diertimoxingyiclc,cleardisp(输入判断矩阵);% 在屏幕显示这句话A=input(A=);% 从屏幕接收判断矩阵[n,n]=size(A);% 计算A的维度,这里是方阵,这么写不太好x=ones(n,100);% x为n行100列全1的矩阵y=ones(n,100);% y同xm=zeros(1,100);% m为1行100列全0的向量m(1)=max(x(:,1));% x第一列中最大的值赋给m的第一个分量y(:,1)=x(:,1);% x的第一列赋予y 的第一列x(:,2)=A*y(:,1);% x的第二列为矩阵A*y(:,1)m(2)=max(x(:,2));% x 第二列中最大的值赋给m的第二个分量y(:,2)=x(:,2)/m(2);% x的第二列除以m(2)后赋给y的第二列p=0.0001;i=2;k=abs(m(2)-m(1));% 初始化p,i,k为m(2)-m(1)的绝对值while k>p% 当k>p是执行循环体i=i+1;% i 自加1x(:,i)=A*y(:,i-1);% x的第i列等于A*y的第i-1列m(i)=max(x(:,i));% m的第i个分量等于x第i列中最大的值y(:,i)=x(:,i)/m(i);% y的第i列等于x的第i列除以m的第i个分量k=abs(m(i)-m(i-1));% k等于m(i)-m(i-1)的绝对值enda=sum(y(:,i));% y的第i列的和赋予aw=y(:,i)/a;% y的第i 列除以at=m(i);% m的第i个分量赋给tdisp(权向量:);disp(w);% 显示权向量wdisp(最大特征值:);disp(t);% 显示最大特征值t %以下是一致性检验CI=(t-n)/(n-1);% t-维度再除以维度-1的值赋给CIRI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准CR=CI/RI(n);% 计算一致性if CR摘要在定性问题的决策中,AHP是一种优秀的方法,其基础是对评价对象的两两比较,并用比较结果构造判断矩阵,而这些都依赖于决策者选用的偏好关系。
8.3.2 层次分析法的计算步骤一、建立层次结构模型运用AHP进行系统分析,首先要将所包含的因素分组,每一组作为一个层次,把问题条理化、层次化,构造层次分析的结构模型。
这些层次大体上可分为3类1、最高层:在这一层次中只有一个元素,一般是分析问题的预定目标或理想结果,因此又称目标层;2、中间层:这一层次包括了为实现目标所涉及的中间环节,它可由若干个层次组成,包括所需要考虑的准则,子准则,因此又称为准则层;3、最底层:表示为实现目标可供选择的各种措施、决策、方案等,因此又称为措施层或方案层。
层次分析结构中各项称为此结构模型中的元素,这里要注意,层次之间的支配关系不一定是完全的,即可以有元素(非底层元素)并不支配下一层次的所有元素而只支配其中部分元素。
这种自上而下的支配关系所形成的层次结构,我们称之为递阶层次结构。
递阶层次结构中的层次数与问题的复杂程度及分析的详尽程度有关,一般可不受限制。
为了避免由于支配的元素过多而给两两比较判断带来困难,每层次中各元素所支配的元素一般地不要超过9个,若多于9个时,可将该层次再划分为若干子层。
例如,大学毕业的选择问题,毕业生需要从收入、社会地位及发展机会方面考虑是否留校工作、读研究生、到某公司或当公务员,这些关系可以将其划分为如图8.1所示的层次结构模型。
图8.1再如,国家综合实力比较的层次结构模型如图6 .2:图6 .2图中,最高层表示解决问题的目的,即应用AHP所要达到的目标;中间层表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等;最低层表示解决问题的措施或政策(即方案)。
然后,用连线表明上一层因素与下一层的联系。
如果某个因素与下一层所有因素均有联系,那么称这个因素与下一层存在完全层次关系。
有时存在不完全层次关系,即某个因素只与下一层次的部分因素有联系。
层次之间可以建立子层次。
子层次从属于主层次的某个因素。
它的因素与下一层次的因素有联系,但不形成独立层次,层次结构模型往往有结构模型表示。
8.3.2 层次分析法的计算步骤一、建立层次结构模型运用AHP 进行系统分析,首先要将所包含的因素分组,每一组作为一个层次,把问题条理化、层次化,构造层次分析的结构模型。
这些层次大体上可分为3 类1、最高层:在这一层次中只有一个元素,一般是分析问题的预定目标或理想结果,因此又称目标层;2、中间层:这一层次包括了为实现目标所涉及的中间环节,它可由若干个层次组成,包括所需要考虑的准则,子准则,因此又称为准则层;3、最底层:表示为实现目标可供选择的各种措施、决策、方案等,因此又称为措施层或方案层。
层次分析结构中各项称为此结构模型中的元素,这里要注意,层次之间的支配关系不一定是完全的,即可以有元素(非底层元素)并不支配下一层次的所有元素而只支配其中部分元素。
这种自上而下的支配关系所形成的层次结构,我们称之为递阶层次结构。
递阶层次结构中的层次数与问题的复杂程度及分析的详尽程度有关,一般可不受限制。
为了避免由于支配的元素过多而给两两比较判断带来困难,每层次中各元素所支配的元素一般地不要超过9 个,若多于9 个时,可将该层次再划分为若干子层。
例如,大学毕业的选择问题,毕业生需要从收入、社会地位及发展机会方面考虑是否留校工作、读研究生、到某公司或当公务员,这些关系可以将其划分为如图8.1 所示的层次结构模型。
图8.1再如,国家综合实力比较的层次结构模型如图6 .2:图 6 .2图中,最高层表示解决问题的目的,即应用AHP 所要达到的目标;中间层表示采用某种措施和政策来实现预定目标所涉及的中间环节,一般又分为策略层、约束层、准则层等;最低层表示解决问题的措施或政策(即方案)。
然后,用连线表明上一层因素与下一层的联系。
如果某个因素与下一层所有因素均有联系,那么称这个因素与下一层存在完全层次关系。
有时存在不完全层次关系,即某个因素只与下一层次的部分因素有联系。
层次之间可以建立子层次。
子层次从属于主层次的某个因素。
它的因素与下一层次的因素有联系,但不形成独立层次,层次结构模型往往有结构模型表示。