05第五章 材料力学习题解答(弯曲内力)

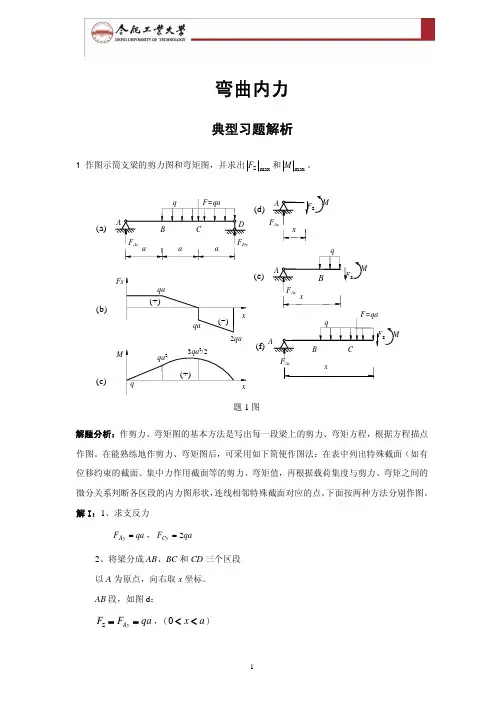
弯曲内力典型习题解析1 作图示简支梁的剪力图和弯矩图，并求出maxSF 和maxM。

解题分析：作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程，根据方程描点作图。

在能熟练地作剪力、弯矩图后，可采用如下简便作图法：在表中列出特殊截面（如有位移约束的截面、集中力作用截面等的剪力、弯矩值，再根据载荷集度与剪力、弯矩之间的微分关系判断各区段的内力图形状，连线相邻特殊截面对应的点。

下面按两种方法分别作图。

解I ：1、求支反力qa F Ay =，qa F Cy 2=2、将梁分成AB 、BC 和CD 三个区段 以A 为原点，向右取x 坐标。

AB 段，如图d ：qa F F Ay ==S ，()a x <<02qa(c)(b)(a)M(d)(e)MSSSM(f)题1图qax x F M Ay ==，()a x ≤≤0BC 段，如图e：)2()(S x a q a x q F F Ay −=−×−=，(a x a 2<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=，(a x a 2≤≤)CD 段，如图f：)()(S x a q F a x q F F Ay −=−−×−=，(a x a 32<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=，(a x a 32≤≤)3、按照步骤2所得各段梁的剪力、弯矩方程画出剪力图和弯矩图，如图b 和图c。

4、计算剪力和弯矩的最大值qa F 2maxS=， 2max23qa M=解II ：1、计算支反力qa F Ay =，qa F Cy2=2、将梁分为AB 、BC 、CD 三个区段，计算每个区段起点和终点的力值。

3、根据载荷情况及微分关系，判断各力区的内力图形状，并以相应的图线连接起来，得到剪力图和弯矩图。

力区 A 截面 AB B 截面 BC C 截面 CD D 截面 载荷 F Ay 向上 q =0无集中力q =负常数 F 向下 q =负常数 F Dy 向上F S突跳F Ay水平(+)连续 下斜线(+) 突减F 下斜线(-) 突跳F DyM 0 上斜线 相切上凸抛物线转折上凸抛物线4、计算剪力弯矩最大值qa F 2maxS=， 2max23qa M=讨论：利用剪力弯矩方程作图时，注意坐标轴x 的正向一般由左至右。

材料力学部分本部分主要内容：一材料力学绪论二轴向拉伸、压缩与剪切三扭转四平面图形的几何性质五弯曲六应力状态与强度理论七组合变形八压杆稳定本部分主要内容：（一）弯曲内力（二）弯曲应力（三）弯曲变形主要内容：一平面弯曲的概念和实例二受弯杆件的简化三剪力和弯矩四剪力方程和弯矩方程·剪力图和弯矩图五剪力、弯矩与分布荷载集度间的关系六弯曲内力部分习题及解答（一）弯曲内力一平面弯曲的概念及实例1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴线变成了曲线，这种变形称为弯曲。

2. 梁：以弯曲变形为主的构件通常称为梁。

3.工程实例一平面弯曲的概念及实例4. 平面弯曲：杆发生弯曲变形后，轴线仍然和外力在同一平面内。

对称弯曲（如下图）——平面弯曲的特例。

非对称弯曲——若梁不具有纵对称面，或者，梁虽具有纵对称面但外力并不作用在对称面内，这种弯曲则统称为非对称弯曲。

本部分内容以对称弯曲为主，讨论梁的应力和变形计算。

一平面弯曲的概念及实例梁的支承条件与载荷情况一般都比较复杂，为了便于分析计算，应进行必要的简化，抽象出计算简图。

1. 构件本身的简化通常取梁的轴线来代替梁。

2. 载荷简化作用于梁上的载荷（包括支座反力）可简化为三种类型：集中力、集中力偶和分布载荷。

3. 支座简化二受弯杆件的简化①固定铰支座2个约束，1个自由度。

如：桥梁下的固定支座，止推滚珠轴承等。

②辊轴支座1个约束，2个自由度。

如：桥梁下的辊轴支座，滚珠轴承等。

二受弯杆件的简化③固定端3个约束，0个自由度。

如：游泳池的跳水板支座，木桩下端的支座等。

q (x )—分布力②悬臂梁二受弯杆件的简化③外伸梁[例] 求下列各图示梁的内力方程并画出内力图。

P Y )x (Q O ==解：①求支反力)L x (P M x Y )x (M O O -=-= ②写出内力方程PLM P Y O O == ;[例]：求图示梁内力图。

xy解：截面法求内力。

11110)(qax M M qax F mi A-=\=+=åxQqa Mqa 2x3qa2/2xqqaa a1122M AY A=S Y 0=S A M 0qa 21M 2qa 2A 2=-+2A qa 21M -=0=-+-A Y qa qa 0=A Y 四剪力方程和弯矩方程·剪力图和弯矩图一、剪力、弯矩与分布荷载间的微分关系对d x 段进行平衡分析，有：[]0d d 0=+-+=å)x (Q )x (Q x )x (q )x (Q Y )x (Q x )x (q d d =五剪力、弯矩与分布荷载集度间的关系及应用()()c x q dxx dQ ==讨论：特别地，当q=c ：1、q=c>0 : 均布载荷向上，则Q 向右上方倾斜的直线2、q=c=0 : 没有均载荷，则Q 为水平直线3、q=c<0: 均布载荷向下，则Q 向右下方倾斜的直线五剪力、弯矩与分布荷载集度间的关系及应用q (x )M (x )+d M (x )Q (x )+d Q (x )Q (x )M (x )d x A0dM(x)][M(x)M(x)q(x)(dx)21Q(x)dx ,0)F (m2i A=+-++=å)Q(x dxdM(x)=弯矩图上某点处的切线斜率等于该点处剪力的大小。

第五章 梁弯曲时的位移 习题解[习题5-1] 试用积分法验算附录IV 中第1至第8项各梁的挠曲线方程及最大挠度、梁端转角的表达式。

解：序号1（1）写弯矩方程（2）写挠曲线近似微分方程，并积分 把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：x M EI EIw e ==θ'，EIxM e =θ 挠曲线方程：221x M EIw e =， EI x M w e 22=（3）求梁端的转角和挠度 解：序号2（1）写弯矩方程（2）写挠曲线近似微分方程，并积分 把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：2'21Fx Flx EI EIw -==θ，)2(22x lx EIF-=θ 挠曲线方程：326121Fx Flx EIw -=，)3(62x l EIFx w -=（3）求梁端的转角和挠度解：序号3（1）写弯矩方程当a x ≤≤0时， Fx Fa x a F x M +-=--=)()( 当l x a ≤≤时， 0)(=x M（2）写挠曲线近似微分方程，并积分当a x ≤≤0时，把边界条件：当0=x 时，0'=w，0=w 代入以上方程得：01=C，02=C。

故：转角方程为：2'21Fx Fax EI EIw -==θ，)2(22x ax EIF-=θ 挠曲线方程：326121Fx Fax EIw -=，)3(62x a EIFx w -=（3）求梁端的转角和挠度设集中力的作用点为C ，则：EI Fa a a a EI F a C 2)2(2)(22=-⋅==θθ EIFa a a EI Fa a w w C 3)3(6)(32=-== 由于CB 段没有外力作用，故该段没有变形，所以：EIFa B 22=θ)233(62)(3tan )(223a a x EIFa EI Fa a x EI Fa a x w w C C B +-=-+≈-+=θ )3(62a x EIFa w B -= 解：序号4（1）写弯矩方程 2)(21)(x l q x M --= （2）写挠曲线近似微分方程，并积分)("x M EIw -= 2")(21x l q EIw -=1322'6)()()(2)(2C x l q x l d x l q dx x l q EIw +--=---=-=⎰⎰ 当0=x 时，0'=w ，即：136)0(0C l q +--=，631ql C =66)(33'ql x l q EIw +--= 23433624)(6)()(6C x ql x l q x ql x l d x l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：24240C ql +=，2442ql C -=24624)(434ql x ql x l q EIw -+-=故：转角方程为：66)(33'ql x l q EIw +--= 挠曲线方程：24624)(434ql x ql x l q EIw -+-=]4)[(24434l x l x l qEIw -+-=)4464(2443432234l x l x lx x l x l l q -++-+-= )46(244322x lx x l q +-= )46(24222x lx l qx +-= （3）求梁端的转角和挠度66)()(33'ql l l q EI l EIw B +--=θEIql B 63=θEIql l l l l ql EIw l EIw B 8)46(24)(4222=+⋅-==解：序号5（1）写弯矩方程l xl q x q -=0)(，lx l q x q )()(0-= lx l q x l l x l q x l x M 6)(3])()(21[)(300--=-⋅-⋅-⋅-=（2）写挠曲线近似微分方程，并积分)("x M EIw -= 30")(6x l lq EIw -=1403030'24)()()(6)(6C lx l q x l d x l l q dx x l l q EIw +--=---=-=⎰⎰ 当0=x 时，0'=w ，即：14024)0(0C l l q +--=，24301l q C =2424)(3040'l q l x l q EIw +--=23050304024120)(24)()(24C x l q l x l q x l q x l d x l l q EIw ++-=+--=⎰ 当0=x 时，0=w 代入以上方程得：250120)0(0C l l q +-=，120402l q C -=12024120)(403050l q x l q l x l q EIw -+-=故：转角方程为：2424)(3040'l q l x l q EIw +--=挠曲线方程：12024120)(403050l q x l q l x l q EIw -+-=)51010(120322320x lx x l l lx q EIw -+-=（3）求梁端的转角和挠度24)(30'l q EI l EIw B ==θ，EIl q B 2430=θ12024120)()(403050l q l l q l l l q EIw l EIw B -⋅+--==， EIl q w B 3040=解：序号6（1）写弯矩方程 l M R A B =（↑），lM R AA = （↓） x lM M x R M x M AA A A -=-=)( （2）写挠曲线近似微分方程，并积分)("x M EIw -= A AM x lM EIw -=" 12'2C x M x lM EIw A A +-=2123216C x C x M x l M EIw A A ++-=把边界条件：当0=x 时，0=w 代入以上方程得：02=C 。

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁，火车的轮轴，楼房的横梁，阳台的挑梁等。

二、弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线。

变形特点——杆轴线由直线变为一条平面的曲线。

三、梁的概念：主要产生弯曲变形的杆。

四、平面弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线，且都在梁的纵向对称平面内（通过或平行形心主轴且过弯曲中心）。

变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。

五、弯曲的分类：1、按杆的形状分——直杆的弯曲；曲杆的弯曲。

2、按杆的长短分——细长杆的弯曲；短粗杆的弯曲。

3、按杆的横截面有无对称轴分——有对称轴的弯曲；无对称轴的弯曲。

4、按杆的变形分——平面弯曲；斜弯曲；弹性弯曲；塑性弯曲。

5、按杆的横截面上的应力分——纯弯曲；横力弯曲。

六、梁、荷载及支座的简化（一）、简化的原则：便于计算，且符合实际要求。

（二）、梁的简化：以梁的轴线代替梁本身。

（三）、荷载的简化：1、集中力——荷载作用的范围与整个杆的长度相比非常小时。

2、分布力——荷载作用的范围与整个杆的长度相比不很小时。

3、集中力偶（分布力偶）——作用于杆的纵向对称面内的力偶。

（四）、支座的简化：1、固定端——有三个约束反力。

2、固定铰支座——有二个约束反力。

3、可动铰支座——有一个约束反力。

（五）、梁的三种基本形式：1、悬臂梁：2、简支梁：3、外伸梁：（L 称为梁的跨长） （六）、静定梁与超静定梁静定梁：由静力学方程可求出支反力，如上述三种基本形式的静定梁。

超静定梁：由静力学方程不可求出支反力或不能求出全部支反力。

§5—2 弯曲内力与内力图一、内力的确定（截面法）：[举例]已知：如图，F ，a ，l 。

求：距A 端x 处截面上内力。

解：①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力：剪力和弯矩1. 弯矩：M ；构件受弯时，横截面上存在垂直于截面的内力偶矩。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( ) 1.2 内力只作用在杆件截面的形心处。

( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。

( ) 1.8 同一截面上各点的正应力ζ必定大小相等，方向相同。

( ) 1.9 同一截面上各点的切应力η必相互平行。

( ) 1.10 应变分为正应变ε和切应变γ。

( ) 1.11 应变为无量纲量。

( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ) 1.13 若物体内各点的应变均为零，则物体无位移。

( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。

1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征是 。

1.4 扭转的受力特征是 ，变形特征是 。

B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。

1.8 所谓 ，是指材料或构件抵抗破坏的能力。

所谓 ，是指构件抵抗变形的能力。

所谓 ，是指材料或构件保持其原有平衡形式的能力。

1.9 根据固体材料的性能作如下三个基本假设 ， ， 。

第四章梁的弯曲内力判断题1. 若两梁的跨度、承受载荷及支承相同，但材料和横截面面积不同，则两梁的剪力图和弯矩图不一定相同。

（X ）2. 最大弯矩必然发生在剪力为零的横截面上。

（X ）3. 若在结构对称的梁上作用有反对称载荷,（V ）4. 简支梁及其承载如图4-1所示，假想沿截面m-m将梁截分为二。

若取梁左段为研究对象，则该截面上的剪力和弯矩与q、M无关；若以梁右段为研究对象，则该截面上的剪力和弯矩与F无关。

（X ）则截面C上的剪力F SC=F ,弯矩M C =2Fa3. 梁段上作用有均布载荷时，剪力图是一条斜直线，而弯矩图是一条抛物线。

4. 当简支梁只受集中力和集中力偶作用时，则最大剪力必发生在集中力作用处c1. 梁在集中力偶作用的截面处，它的内力图为（ C ）cA Fs图有突变，M图无变化;B Fs图有突变，M图有转折;C M 图有突变，Fs图无变化;D M图有突变，Fs图有转折。

填空题2•图4-3所示外伸梁ABC，承受一可移动载荷 F ,若F、I均为已知，为减小梁的最大弯矩值，则外伸段的合理长度a= _J/3 ________ 。

图4-2 图4-3则该梁具有对称的剪力图和反对称的弯矩图。

1•图4-2所示为水平梁左段的受力图,选择题2. 梁在集中力作用的截面处，它的内力图为（B ）cA Fs有突变，M图光滑连续;B Fs有突变，M图有转折;C M图有突变，凡图光滑连续；D M图有突变，Fs图有转折。

3. 在图4-4所示四种情况中，截面上弯矩M为正，剪力Fs为负的是（B ）cf s (C)图4-44.梁在某一段内作用有向下的分布力时，则在该段内，M 图是一条(A )。

A 上凸曲线；B 下凸曲线；C 带有拐点的曲线 ；D 斜直线。

5•多跨静定梁的两种受载情况分别如图4-5 ( a )、( b )所示，以下结论中( A )是正确的。

力 F靠近铰链。

tli ＞弯矩图 图4-6F. FsI A)A C 6. 图4-5Fs 图和M 图完全相同Fs 图不同，M 图相同 两者的两者的 若梁的剪力图和弯矩图分别如图AB 段有均布载荷 AB；D4-6 ( a ) Fs 相同对图不同； Fs 图和M 图均不相同。

5-1构件受力如图5-26所示。

试：(1)确定危险点的位置；(2)用单元体表示危险点的应力状态（即用纵横截面截取危险点的单元体，并画出应力）。

题5-1图解：a) 1) 危险点的位置：每点受力情况相同，均为危险点；2）用单元体表示的危险点的应力状态见下图。

b) 1) 危险点的位置：外力扭矩3T与2T作用面之间的轴段上表面各点；2）应力状态见下图。

c) 1) 危险点：A点，即杆件最左端截面上最上面或最下面的点；2）应力状态见下图。

d) 1）危险点：杆件表面上各点；2）应力状态见下图。

5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值，并指出属于哪一种应力状态（应力单位为MPa）。

10题5-2图AAT（a）（c）（d）364dFlπτ=a) b) c) d)a) b) c)解： a) 1σ=50 MPa, 2σ=3σ=0,属于单向应力状态b) 1σ=40 MPa, 2σ=0, 3σ=－30 MPa ，属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=－30 MPa ，属于三向应力状态5-3已知一点的应力状态如图5-28所示（应力单位为MPa ）。

试用解析法求指定斜截面上的正应力和切应力。

题5-3图解：a) 取水平轴为x 轴，则根据正负号规定可知： x σ=50MPa , y σ=30MPa , x τ=0, α=－30 带入式（5-3），（5-4）得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴，根据正负号规定：x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式，得：240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴，则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得：60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPaa)b)c)5-4已知一点的应力状态如图5-29所示（应力状态为MPa ）。