材料力学典型例题及解析 4.弯曲内力典型习题解析
- 格式:pdf
- 大小:281.41 KB
- 文档页数:7


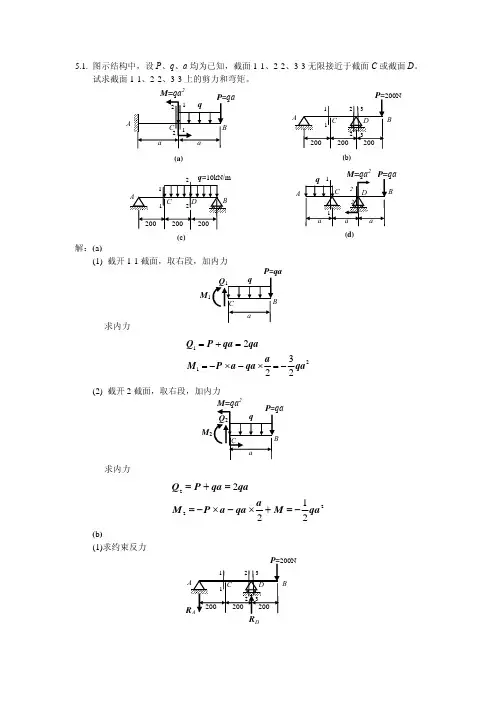
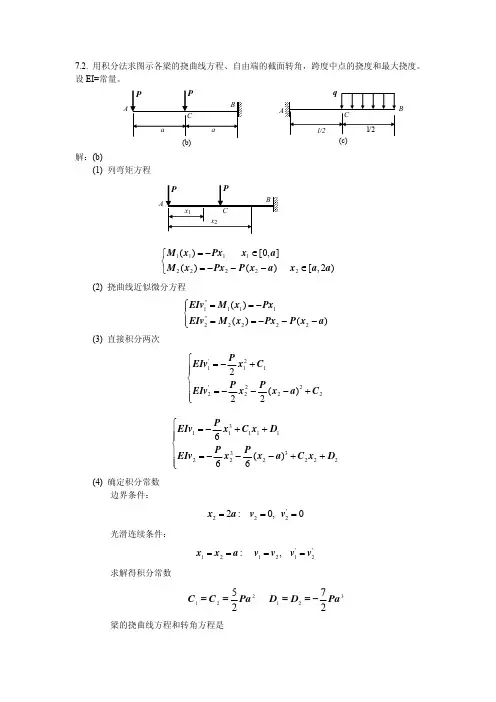





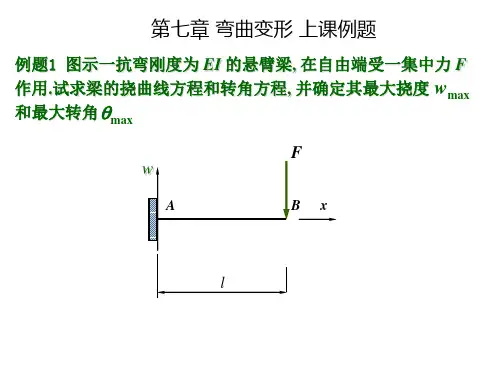

第四章弯曲应力判断图弯矩的值等于梁截面一侧所有外力的代数和。
()负弯矩说明该截面弯矩值很小,在设计时可以忽略不计。
()简支梁上向下的集中力对任意横截面均产生负弯矩。
()横截面两侧所有外力对该截面形心力矩的代数和就是该截面的弯矩值。
()梁的任一横截面上的弯矩在数值上等于该截面任一侧所有外力对该截面形心的力矩代数和。
()在计算指定截面的剪力时,左段梁向下的荷载产生负剪力。
()在计算指定截面的剪力时,右段梁向下的荷载产生正剪力。
()梁纯弯曲时中性轴一定通过截面的形心。
()简支梁上受一集中力偶作用,当集中力偶在不改变转向的条件下,在梁上任意移动时,弯矩图发生变化,剪力图不发生变化。
()图示梁弯矩图的B点是二次抛物线的顶点。
()图示梁段上集中力偶作用点两侧的弯矩直线一定平行。
()(M图)下列三种斜梁A截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁B截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁C截面的弯矩均相同。
()l/2l/2l/2l/2l/2l/2梁弯曲时的内力有剪力和弯矩,剪力的方向总是和横截面相切,而弯矩的作用面总是垂直于横截面。
()一端(或两端)向支座外伸出的简支梁叫做外伸梁。
()##√悬臂梁的一端固定,另一端为自由端。
()##√弯矩的作用面与梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
()##√弯曲时剪力对细长梁的强度影响很小,所以在一般工程计算中可忽略。
()##√图示,外伸梁BC段受力F作用而发生弯曲变形,AB段无外力而不产生弯曲变形()##×由于弯矩是垂直于横截面的内力的合力偶矩,所以弯矩必然在横截面上形成正应力。
()##√抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
()##×无论梁的截面形状如何,只要截面面积相等,则抗弯截面系数就相等。
()##×梁弯曲变形时,弯矩最大的截面一定是危险截面。
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
弯曲内力
典型习题解析
1 作图示简支梁的剪力图和弯矩图,并求出max
S
F 和max
M。
解题分析:作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程,根据方程描点作图。
在能熟练地作剪力、弯矩图后,可采用如下简便作图法:在表中列出特殊截面(如有位移约束的截面、集中力作用截面等的剪力、弯矩值,再根据载荷集度与剪力、弯矩之间的微分关系判断各区段的内力图形状,连线相邻特殊截面对应的点。
下面按两种方法分别作图。
解I :1、求支反力
qa F Ay =,
qa F Cy 2=2、将梁分成AB 、BC 和CD 三个区段 以A 为原点,向右取x 坐标。
AB 段,如图d :
qa F F Ay ==S ,()
a x <<0
2qa
(c)
(b)
(a)
M
(d)
(e)
M
S
S
S
M
(f)
题1图
qax x F M Ay ==,()
a x ≤≤0BC 段,如图e:
)2()(S x a q a x q F F Ay −=−×−=,(a x a 2<<)
)/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 2≤≤)
CD 段,如图f:
)()(S x a q F a x q F F Ay −=−−×−=,(a x a 32<<)
)/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 32≤≤)
3、按照步骤2所得各段梁的剪力、弯矩方程画出剪力图和弯矩图,如图b 和图c。
4、计算剪力和弯矩的最大值
qa F 2max
S
=, 2max
2
3qa M
=
解II :1、计算支反力
qa F Ay =,
qa F Cy
2=2、将梁分为AB 、BC 、CD 三个区段,计算每个区段起点和终点的力值。
3、根据载荷情况及微分关系,判断各力区的内力图形状,并以相应的图线连接起来,得到剪力图和弯矩图。
力区 A 截面 AB B 截面 BC C 截面 CD D 截面 载荷 F Ay 向上 q =0
无集中力q =负常数 F 向下 q =负常数 F Dy 向上F S
突跳F Ay
水平(+)
连续 下斜线(+) 突减F 下斜线(-) 突跳F Dy
M 0 上斜线 相切
上凸抛物线
转折
上凸抛物线
4、计算剪力弯矩最大值
qa F 2max
S
=, 2
max
2
3qa M
=
讨论:利用剪力弯矩方程作图时,注意坐标轴x 的正向一般由左至右。
有时候根据需要,可
以取为由右至左,但此时必须注意q ,F S 和M 之间的微分关系在正负号上有变化。
2 作图示梁的剪力图和弯矩图。
解题分析:不分段列剪力、弯矩方程,只计算特殊截面处的剪力、弯矩值,根据规律连线。
解:1、求支反力
qa F qa F Cy Ay 5
4
,43==
2、计算特殊截面剪力值
将梁分为三个区段计算每个截面的值。
集中力作用截面的左、右两侧值不同。
S F S F qa F F A A 4
3
0S S ==右左, qa F qa F B B 41
43S S −==
右左, qa F qa F C C =−=右左,S S 4
1
0S =D F
3、计算特殊截面弯矩值
计算前述特殊截面处的M 值。
集中力偶作用截面的左、右两侧的M 值不同。
0=A M 224
1
43qa M qa M B B −==
右左, 题2图
22
1qa M C −
= 0=D M
CD 段是二次抛物线,抛物线上有极值时应求出。
4、计算最大剪力和弯矩值
qa F =max
S
, 2max
4
3qa M
=
讨论:采用上述作图法不能遗漏代表点,包括载荷变化点、约束点。
计算极值弯矩时,可以先找出该区段剪力为零的截面,该截面处的弯矩即为极值弯矩。
也可以借助该区段的弯矩方程计算极值。
3 作图示梁的剪力图和弯矩图,并求出max
S
F 及max
析:梁上有中间铰时M
,B 处是中间铰。
解题分,先自铰处将梁拆分。
中矩一定为零。
解: 1、求支反力
间铰可以传递力,但不能传递弯矩,所以中间铰处弯在中间铰B 处将梁拆开两部分,铰处互相作用
力用By F 代替,如图b 所示。
24
7
,47,1qa F F qa F By Ay ==4qa M A Dy ==
2、将梁分为AB 、BC 、CD 三个区段,计算A B 、
C D 截面处的内力值。
3、集度与剪力、弯矩之间的微分关系,
4、CD 段剪力有零点,根据左负右正,判断弯矩图有极小值。
、、根据载荷判断各区段的内力图形状,并用图线连接。
令041)(S x F =−=
qx qa ,得a x 4
1
=,代入弯矩方程
2232
1)4(2141)(qa a q a F x M D =+×−=
5、计算最大剪力、弯矩值
qa F 4
max
S
=
, 7
2max
4
M =
7qa F S
(d) M
题3图
4 试作图示梁的剪力图和弯矩图
解题分析:对于三角形()q 0的关系,再列出剪力、弯矩方程。
结构和载荷均对称时,弯矩图对称,剪力图反对称。
所以,只须取左半边作图,然后根据上述对称解: 1、求支反力
分布载荷,先列出q x 和反对称关系,画出另一半剪力、弯矩图。
l q F F Cy Ay =
=04
1
2、列、S F M 方程
l
x q x q (0
= 2))20(41)(21
41)(20
00l −S1l
x l x q l q x x q q x F <<−==
)2
l
0(3432)(41)(30001x x l
q lx q
x x x q lx q x M ≤≤−=⋅−=
2
l
x =
处M 为极大值。
2030)()(1l q l l M −=
0max 12
1
2324l q l q = 3、作、S F M 图
AB 段, 图为二次抛物线,S F M 图为三次抛物线。
BC 段,图与AB 段反对称,S F M 图与AB 段对称。
4、计算最大剪力弯矩值
q 0l /4
(+)
q 0l 2/12
(+)
(-)
题4q 0l /4
图
4
0l
q =
max
S
F ,21
l q M =
0max
12
5 作图示刚架的内力图
C 铰处拆开,得:
解题分析:刚架有中间铰,自铰处拆开,先求支反力,然后根据对称规律作剪力、弯矩图。
铰处无集中载荷时,铰两侧轴力、剪力图连续,弯矩为零。
解:1、求支反力
由于对称 qa F F Ey Ay == 在Ex Ax F qa
F ==
4
2、作F 图
N AB 力区,直线; ,区,qa F −=N ,BC CD 力4
N qa
F −
=,直线; 力区,,直线。
3、DE qa F −=N 作S F 图
AB 力区,0=q ,4
S qa
−
=直线F
D 2/2
题5图
qa
BD 力区,等于负常数,图为斜线,q S F qa F =max
S
DE 力区,,0=q 4
S qa
F =直线 4、作M 图
AB 力区,S F 为负常数,M 图为斜线。
BC 力区,为斜线,正值,S F M 图为二次抛物线,C 处M 值等于零。
CD 力区,为斜线,负值,S F M 图为二次抛物线。
2
2
DE 力区,为正常数,M 图为斜线。
S F max
M
=。
qa 讨论:作称性或反对称性可以大大降低工作量。
刚架内力图时充分利用刚架的几何对称性、载荷的对。