第四章弯曲内力(习题解答)

弯曲力1. 长l的梁用绳向上吊起，如图所示。

钢绳绑扎处离梁端部的距离为x。

梁由自重引起的最大弯矩|M|max为最小时的x值为：(A) /2l；(B) /6l；(C…) 1)/2l。

l；(D) 1)/22. 多跨静定梁的两种受载情况如图(a)、(b)所示。

下列结论中哪个是正确的？(A) 两者的剪力图相同，弯矩图也相同；(B) 两者的剪力图相同，弯矩图不同；(C) 两者的剪力图不同，弯矩图相同；(D….) 两者的剪力图不同，弯矩图也不同。

3. 图示(a)、(b)两根梁，它们的(A) 剪力图、弯矩图都相同；(B…) 剪力图相同，弯矩图不同；(C) 剪力图不同，弯矩图相同；(D) 剪力图、弯矩图都不同。

4. 图示梁，当力偶M e的位置改变时，有下列结论：(A) 剪力图、弯矩图都改变；(B…) 剪力图不变，只弯矩图改变；(C) 弯矩图不变，只剪力图改变；(D) 剪力图、弯矩图都不变。

5. 图示梁C截面弯矩M C = ；为使M C =0，则M e= ；为使全梁不出现正弯矩，则M e≥。

6. 图示梁，已知F、l、a。

使梁的最大弯矩为最小时，梁端重量P= 。

7. 图示梁受分布力偶作用，其值沿轴线按线性规律分布，则B端支反力为，弯矩图为 次曲线，|M |max 发生在 处。

8. 图示梁，m (x )为沿梁长每单位长度上的力偶矩值，m (x )、q (x )、F S (x )和M (x )之间的微分关系为：S d ();d F x x = d ()d M x x = 。

9. 外伸梁受载如图，欲使AB 中点的弯矩等于零时，需在B 端加多大的集中力偶矩（将大小和方向标在图上）。

10. 简支梁受载如图，欲使A 截面弯矩等于零时，则=e21e /M M 。

1-10题答案：1. C 2. D 3. B 4. B 5. 28e2M ql -；42ql ；22ql 6. ⎪⎭⎫⎝⎛-a l a F 24 7. m 0/2；二；l /28. q (x )；F S (x )+ m (x ) 9. 10. 1/211-60题. 作图示梁的剪力图和弯矩图。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。

( ) 1.2 内力只作用在杆件截面的形心处。

( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。

( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。

( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。

( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。

( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。

( ) 1.8 同一截面上各点的正应力ζ必定大小相等，方向相同。

( ) 1.9 同一截面上各点的切应力η必相互平行。

( ) 1.10 应变分为正应变ε和切应变γ。

( ) 1.11 应变为无量纲量。

( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。

( ) 1.13 若物体内各点的应变均为零，则物体无位移。

( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。

( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。

( )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。

( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。

1.2 拉伸或压缩的受力特征是 ，变形特征是 。

1.3 剪切的受力特征是 ，变形特征是 。

1.4 扭转的受力特征是 ，变形特征是 。

B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。

1.6 组合受力与变形是指 。

1.7 构件的承载能力包括 ， 和 三个方面。

1.8 所谓 ，是指材料或构件抵抗破坏的能力。

所谓 ，是指构件抵抗变形的能力。

所谓 ，是指材料或构件保持其原有平衡形式的能力。

1.9 根据固体材料的性能作如下三个基本假设 ， ， 。

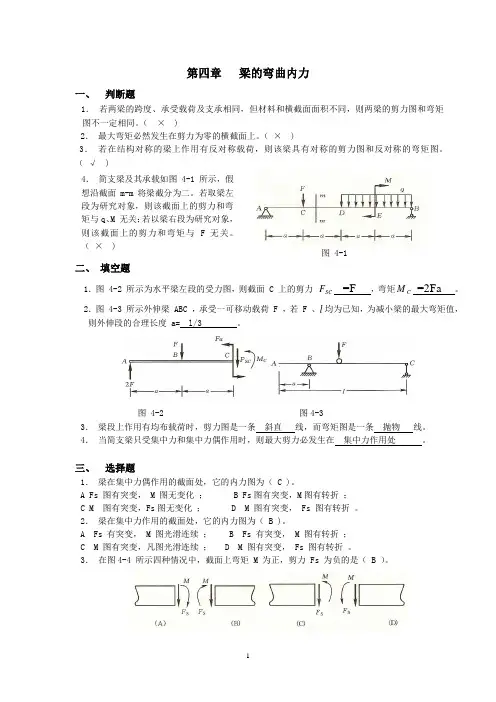
第四章 梁的弯曲内力一、 判断题1． 若两梁的跨度、承受载荷及支承相同，但材料和横截面面积不同，则两梁的剪力图和弯矩图不一定相同。

（ × )2． 最大弯矩必然发生在剪力为零的横截面上。

（ × )3． 若在结构对称的梁上作用有反对称载荷，则该梁具有对称的剪力图和反对称的弯矩图。

图 4-1 二、 填空题1．图 4-2 所示为水平梁左段的受力图，则截面 C 上的剪力 SC F =F ，弯矩C M =2Fa 。

2．图 4-3 所示外伸梁 ABC ，承受一可移动载荷 F ，若 F 、l 均为已知，为减小梁的最大弯矩值，则外伸段的合理长度 a= l/3 。

图 4-2 图4-33． 梁段上作用有均布载荷时，剪力图是一条 斜直 线，而弯矩图是一条 抛物 线。

4． 当简支梁只受集中力和集中力偶作用时，则最大剪力必发生在 集中力作用处 。

三、 选择题1． 梁在集中力偶作用的截面处，它的内力图为（ C )。

A Fs 图有突变， M 图无变化 ；B Fs 图有突变，M 图有转折 ；C M 图有突变，Fs 图无变化 ；D M 图有突变， Fs 图有转折 。

2． 梁在集中力作用的截面处，它的内力图为（ B )。

A Fs 有突变， M 图光滑连续 ；B Fs 有突变， M 图有转折 ；C M 图有突变，凡图光滑连续 ；D M 图有突变， Fs 图有转折 。

3． 在图4-4 所示四种情况中，截面上弯矩 M 为正，剪力 Fs 为负的是（ B ）。

图 4-44．梁在某一段内作用有向下的分布力时，则在该段内， M 图是一条（ A ）。

A 上凸曲线； B下凸曲线；C 带有拐点的曲线；D 斜直线。

5．多跨静定梁的两种受载情况分别如图4-5 ( a ）、（ b ）所示，以下结论中（ A ）是正确的。

力F 靠近铰链。

图4-5A 两者的 Fs 图和 M 图完全相同；B 两者的 Fs 相同对图不同；C 两者的 Fs 图不同， M 图相同；D 两者的Fs图和 M 图均不相同。

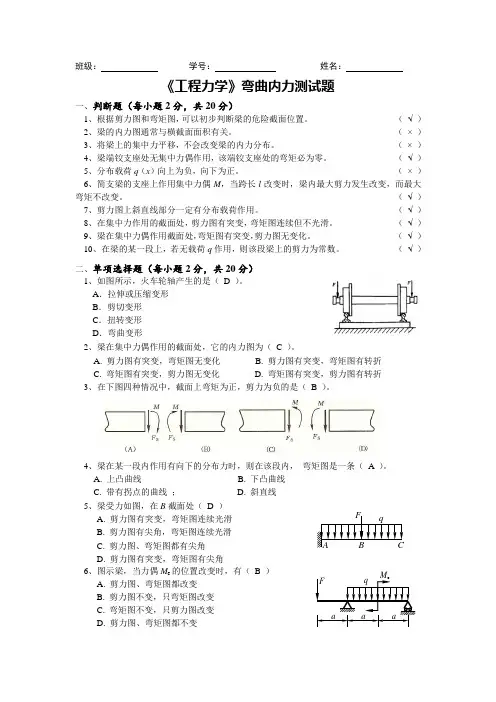
班级：学号：姓名：《工程力学》弯曲内力测试题一、判断题（每小题2分，共20分）1、根据剪力图和弯矩图，可以初步判断梁的危险截面位置。

（√）2、梁的内力图通常与横截面面积有关。

（×）3、将梁上的集中力平移，不会改变梁的内力分布。

（×）4、梁端铰支座处无集中力偶作用，该端铰支座处的弯矩必为零。

（√）5、分布载荷q（x）向上为负，向下为正。

（×）6、简支梁的支座上作用集中力偶M，当跨长l改变时，梁内最大剪力发生改变，而最大弯矩不改变。

（√）7、剪力图上斜直线部分一定有分布载荷作用。

（√）8、在集中力作用的截面处，剪力图有突变，弯矩图连续但不光滑。

（√）9、梁在集中力偶作用截面处，弯矩图有突变，剪力图无变化。

（√）10、在梁的某一段上，若无载荷q作用，则该段梁上的剪力为常数。

（√）二、单项选择题（每小题2分，共20分）1、如图所示，火车轮轴产生的是（D ）。

A．拉伸或压缩变形B．剪切变形C．扭转变形D．弯曲变形2、梁在集中力偶作用的截面处，它的内力图为（C ）。

A. 剪力图有突变，弯矩图无变化B. 剪力图有突变，弯矩图有转折C. 弯矩图有突变，剪力图无变化D. 弯矩图有突变，剪力图有转折3、在下图四种情况中，截面上弯矩为正，剪力为负的是（B ）。

4、梁在某一段内作用有向下的分布力时，则在该段内，弯矩图是一条（A ）。

A. 上凸曲线B. 下凸曲线C. 带有拐点的曲线；D. 斜直线5、梁受力如图，在B截面处（D ）A. 剪力图有突变，弯矩图连续光滑B. 剪力图有尖角，弯矩图连续光滑C. 剪力图、弯矩图都有尖角D. 剪力图有突变，弯矩图有尖角6、图示梁，当力偶M e的位置改变时，有（B ）A. 剪力图、弯矩图都改变B. 剪力图不变，只弯矩图改变C. 弯矩图不变，只剪力图改变D. 剪力图、弯矩图都不变F qCBAFM eaqa a7、若梁的受力情况对于梁的中央截面为反对称（如图），则下列结论中正确的是（D ）A. 剪力图和弯矩图均为反对称，中央截面上剪力为零B. 剪力图和弯矩图均为对称，中央截面上弯矩为零C. 剪力图反对称，弯矩图对称，中央截面上剪力为零D. 剪力图对称，弯矩图反对称，中央截面上弯矩为零8、多跨静定梁的两种受载情况分别如图所示，力F靠近铰链，以下结论正确的是（C ）A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同，弯矩图不同C. 两者的剪力图不同，弯矩图相同D. 两者的剪力图和弯矩图均不相同9、多跨静定梁的两种受载情况如图所示，下列结论中正确的是（D ）A. 两者的剪力图和弯矩图完全相同B. 两者的剪力图相同，弯矩图不同C. 两者的剪力图不同，弯矩图相同D. 两者的剪力图和弯矩图均不相同10、若梁的剪力图和弯矩图分别如图所示，则该图表明（C ）A. AB段有均布载荷，BC段无载荷；B. AB 段无载荷，B截面处有向上的集中力，BC段有向下的均布载荷；C. AB 段无载荷，B截面处有向下的集中力，BC段有向下的均布载荷；D. AB 段无载荷，B截面处有顺时针的集中力偶，BC段有向下的均布载荷。

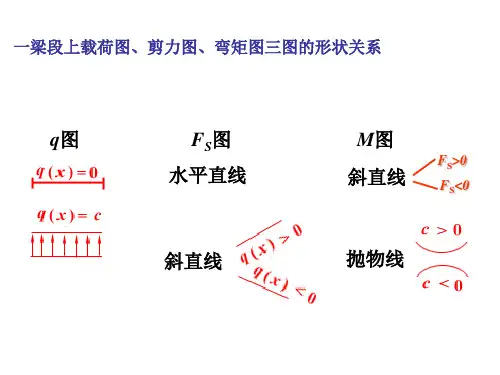
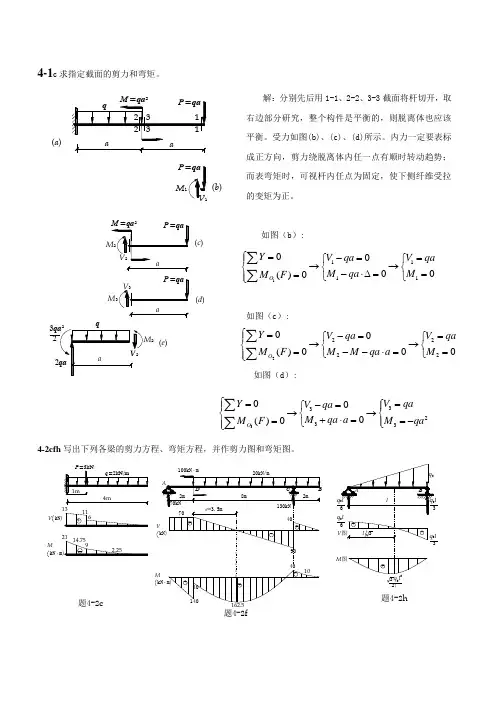
解：分别先后用1-1、2-2、3-3截面将杆切开，取右边部分研究，整个构件是平衡的，则脱离体也应该平衡。

受力如图(b)、(c)、(d)所示。

内力一定要表标成正方向，剪力绕脱离体内任一点有顺时转动趋势；而表弯矩时，可视杆内任点为固定，使下侧纤维受拉的变矩为正。

如图（b ）:如图（c ）:如图（d ）:4-1c 求指定截面的剪力和弯矩。

4-2cfh 写出下列各梁的剪力方程、弯矩方程，并作剪力图和弯矩图。

题4-2cV MkN ·题4-2f·题4-2h230q l 27(a )(b )M P 111110000()0O Y V qa V qa M qa M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨-⋅∆===⎩⎩⎪⎩∑∑2(e )M (d )a(c )a333233000()0O Y V qa V qa M qa a M qa M F ⎧==-=⎧⎧⎪⎪→→⎨⎨⎨+⋅==-=⎪⎩⎩⎪⎩∑∑222220000()0O Y V qa V qa M M qa a M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨--⋅===⎩⎩⎪⎩∑∑4-3dfgh 用微分关系作下列各梁的剪力图和弯矩图4kN ·m+题4-3d10.25MkN ·m)VkN)--1243.5-10.25-+322+-题4-3fM 图85Pl 83Pl 16Pl P/4-43.5--12MkN ·m)V kN)24++-26.257.57.5题4-3g5P/4+P=15kN+-24313.875313.875qaM 图V 图2qa +-2+-2+-qa2qa题4-3hMkN ·V kN)3.1254-6 起吊一根自重为q （N/m ）的等截面钢筋混凝土梁，问起吊点的合理位置x 应为多少（令梁在吊点处和中点处的最大正负弯矩的绝对值相等）MkN ·m)V kN)题4-6+2ql(l-2x)/4-q l /8qx/22qx/2qx ql/2-qx ql/2-qxqx--+--+q22qx/8qx/82题4-74-7天车梁上小车轮距为c ，起重量为P ，问小车走到什么位置时，梁弯矩最大？并求出最大弯矩。

q 2qa a a a
A C
D
B
第四章 弯曲内力习题
一、填空题
1、如果一段梁内各横截面上的剪力Q 为零，而弯矩M 为常量，则该段梁的弯曲称为 ；如果该梁各横截面上同时存在剪力Q 和弯矩M ，则这种弯曲为 。

二、计算题
1、作下列两梁的弯矩图。

求出支座处的约束反力、弯矩的最大绝对值，并把该值标注在弯矩图上。

2、作下列梁的弯矩图。

求出支座处的约束反力、弯矩的最大绝对值，并把该值标注在弯矩图上。

3、下列梁的弯矩图。

第四章 弯曲内力习题答案
一、填空题
1 纯弯曲 横力弯曲（或剪切弯曲）
二、计算题
1、 图4.2.2 图4.2.4.1 图4.2.4.2
图4.2.4.3 Pa
25
6q a 22
3q a
2、
3、
22m ax 22B B ql R ql M ql M === 15.75kN 20.25kN 41kN.m
A D m ax R =R =M =m ax A
B R R P M P a
===⨯2m ax 716656A B R qa R qa M qa ==-
= 22q l。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a 所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。