基于Matlab的模糊PID控制器的设计和仿真

基于MATLAB模糊自适应PID 控制器的设计The fuzzy PID controller and‘its simulation Abstract：This paper discusses the design of fuzzy PID controller and he method of realization using MATLAB software．The result of simulation in MATLAB／Simulink indicates that the controlle r evidently improves the dynamic property of control system．The controlle r is easily realized and applied in engineering．First, let's take a look at how the PID controller works in variable (e) represents the tracking error, the difference between the desired input value (R) and the actual output (Y). This error signal (e) will be sent to the PID controller, and the controller computes both the derivative and the integral of this error signal. The signal (u) just past the controller is now equal to the proportional gain (Kp) times the magnitude of the error plus the integral gain (Ki) times the integral of the error plus the derivative gain (Kd) times the derivativeof the error.摘要: 基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整摘要: 基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。

自适应模糊PID控制仿真报告
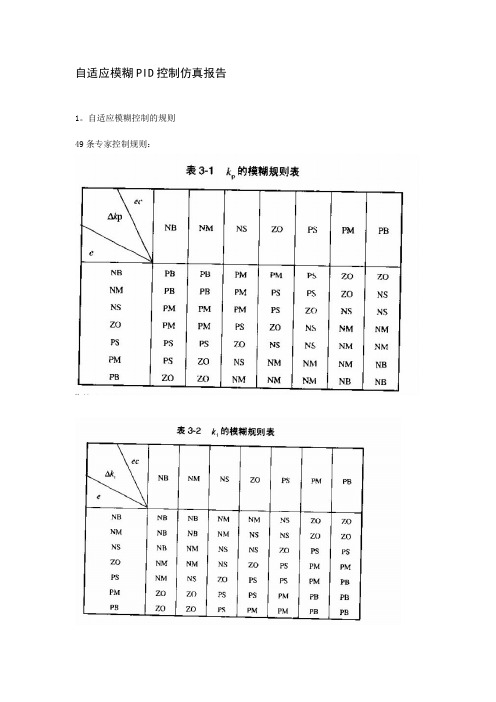
1。

自适应模糊控制的规则
49条专家控制规则：
2。

系统仿真框图
包括模糊控制器，PID控制器两部分组成。

3.模糊控制器设计
确定为双输入,三输出结构
确定每个变量的论域，其中每个变量都有一个模糊子集来表示。

这个模糊子集中有7个语言变量,分别是：NB，NM，NS,ZO,PS,PM,PB
在编辑界面中，确定好每一个语言变量的范围,以及隶属函数的类型。

如下图所示：
输入模糊控制规则：
仿真结果
PID控制器Kp参数在控制过程中的变化曲线：
Ki参数：
Kd参数：
系统闭环控制阶跃响应曲线：
传统PID控制响应曲线：(ZN整定法）
对比可以发现，自适应模糊PID控制不仅使曲线超调量小，响应过程平稳，而且动态响应时间也较短.性能优于传统PID控制器。

对比如下：(PID采用cohen-coon整定法）红色为常规PID控制器，黄色为模糊PID控制器
采用ZN法整定后对比：
而且在仿真中发现一个问题：ZN法整定存在不稳定问题，但模糊控制则非常平稳
加干扰的控制对比系统框图
对比效果:
对应的模糊PID参数变化情况: P
PI
PD。

万方数据２００６年第２期·控制与检测·糊自整定ＰＩＤ控制器如图１所示。

模糊自整定ＰＩＤ是在ＰＩＤ算法的基础上通过计算当前系统误差ｅ和误差变化率ｅｃ，利用模糊规则进行模糊推理，再查询模糊矩阵表进行参数调整。

其设计核心是总结工程设计人员的技术知识和实际操作经验，建立合适的模糊规则表。

我们按如下方法进行了ｋ。

、ｋ。

、ｋ。

三个参数的自适应校正：（１）确定输入变量，并将其模糊化通过实测值与理想值比较求出误差值ｅ及误差变化率ｅｃ作为输入变量，定义ｅ、ｅｃ模糊量的模糊子集为：｛ＮＢ，ＮＭ，ＮＳ，ｚＤ，ＰＳ，ＰＭ，ＰＢ｝，子集中元素分别代表负大，负中、负小、零、正小、正中、正大。

论域为｛－６，６｝。

（２）确定输出变量和隶属函数以Ｋ、Ｋ、弼三个参数作为输出变量，Ｋ、Ｋ、心模糊量的模糊子集为：｛ＮＢ，ＮＭ，ＮＳ，ＺＯ，ＰＳ，聊，Ｐ曰｝，Ｋ的论域为｛－０．３，０．３｝，Ｋ的论域为｛－０．０６，０．０６｝，％的论域为｛一３，３｝。

考虑论域的覆盖程度和灵敏度，以及为了调整方便，以上各模糊子集均选用三角形隶属函数。

（３）确定模糊控制规则模糊推理的核心是“ＩＦ…ＴＨＥＮ”形式的模糊控制规则。

控制规则的选取直接关系到系统控制性能的优劣。

我们假设根据现有经验，经过现场反复调试，分别制定了三个输出参数的模糊控制规则表如表１～表２所示。

表１ｋｚ参数的模糊控制规则表”—而—■而——丽——历——面——而ｒ—而ＮＢＰＢＰＢＰＭＰＭＰｓＺＯＮｓＮＭＰＢＰＢＰＭＰｓＰｓｚｏＮｓＮｓＰＭＰＭＰＭＰｓｚｏＮｓＮｓＺＤＰＭＰＭＰｌｓＺＯＮｓＮＭＮＭＰｓＰＳＰｓＺＯＮＳＮＳＮＭＮＭＰＭＰ＿ｓＺ０ＮｓＮＭＮＭＮＭＮＢＰＢＺＤＺ０ＮＭＮＭＮＭＮＢＮＢ表２屯、虬参数的模糊控制规则表ＮＢＮＢＮＢＮＭＮＭＮｓＺＤＺ０ＮＭＮＢＮＢＮＭＮＳＮｓＺＤＺ０ＮＳＮＢＮＭＮｓＮＳＺ０ＰＳＰＳＺＤＮＭＮＭＮｓＺ０Ｐ＿ｓＰＭＰＭＰＳＮＭＮｓＺＤＮｓＰＳＰＭＰＢＰＭＺＯＺＤＰＳＰｓＰＭＰＢＰＢＰＢＺ０Ｚ０ＰｓＰＭＰＭＰＢＰＢ（４）在线自适应校正模糊规则制定以后，设ｅ、ｅｃ、Ｋ、Ｋ。

Industry Control and Applications基于MAT LAB的PID参数模糊自整定控制器设计及仿真张　敏1,余　纯2(1.武汉化工学院电气信息学院,湖北　武汉　430074; 2.江汉大学数学与计算机学院,湖北　武汉　430056)摘要:本文针对时滞、参数时变和有干扰的控制系统,提出基于M AT LAB的PI D参数模糊自整定控制器的设计与仿真。

本文利用G UI(图形用户界面)建立模糊控制器,仿真模型为二阶延迟系统。

仿真结果表明,系统阶跃响应具有较好的动态特性和鲁棒性,表明该PI D参数模糊自整定控制器有较高的实用性。

关键词:PI D控制;模糊控制;PI D参数模糊自整定;计算机仿真中图分类号:TP23714　文献标识码:B　文章编号:100327241(2005)0720022204MAT LAB-Bas e d Desig n of A Fuzzy-Tu n nin gPID Co ntrollerZHANG Min1,YU Chun2(11Institute of In formation and Engineering,Wuhan Chemical Industry C ollege,Wuhan430074,China;21C ollege of Math1&C om puter Science,Jianghan University,Wuhan430056,China)Abstract:This paper presents the design of the fuzzy-tunning PI D controller based on M AT LAB1I t uses G UI(G raphical User Inter face)to constructa fuzzy controller and a plant of a second-order with delay1S imulation results show that the system has better dynamic character and ro2bustness1K ey w ords:PI D control;Fuzzy control;Fuzzy self-tuning PI D;C om puter simulation1　引言模糊控制器和常规的控制器(如PI D调节器)相比具有无须建立被控对象的数学模型,对被控对象的时滞、非线性和时变性具有一定的适应能力等优点,同时对噪声也具有较强的抑制能力,即鲁棒性较好。

基于MATLAB的PID控制器参数整定及仿真PID控制器是一种经典的控制器，在工业自动化控制系统中广泛应用。

其主要功能是根据系统的误差信号，通过调整输出信号的比例、积分和微分部分来减小误差，并达到系统的稳定控制。

PID控制器参数整定是指确定合适的比例常数Kp、积分常数Ki和微分常数Kd的过程。

本文将介绍基于MATLAB的PID控制器参数整定及仿真的方法。

首先，在MATLAB中建立一个包含PID控制器的模型。

可以通过使用MATLAB的控制系统工具箱来实现这一过程。

在工具箱中，可以选择合适的建模方法，如直接设计模型、积分节点模型或传输函数模型。

通过这些工具，可以方便地建立控制系统的数学模型。

其次，进行PID控制器参数整定。

PID控制器参数整定的目标是通过调整比例常数Kp、积分常数Ki和微分常数Kd，使系统的响应特性达到最佳状态。

常用的PID参数整定方法有经验法、试误法、Ziegler-Nichols方法等。

1.经验法：根据系统的特性和经验，选择合适的PID参数。

这种方法常用于初步整定，但可能需要根据实际情况调整参数。

2.试误法：通过逐步试验和调整PID参数，使系统的输出响应逐渐接近期望值，从而达到最佳控制效果。

3. Ziegler-Nichols方法：该方法是一种经典的系统辨识方法，通过测试系统的临界稳定性，得到系统的传递函数参数，并据此计算出合适的PID参数。

最后，进行PID控制器参数整定的仿真。

在MATLAB中，可以通过使用PID模块进行仿真。

可以输入相应的输入信号和初始参数，观察系统的输出响应，并通过调整参数，得到最佳的控制效果。

总结起来，基于MATLAB的PID控制器参数整定及仿真的过程包括：建立控制系统模型、选择PID参数整定方法、进行PID参数整定、进行仿真实验。

PID控制器参数整定的好坏直接影响控制系统的工作性能。

通过基于MATLAB的仿真实验，可以方便地调整和优化控制系统的PID参数，提高系统的响应速度、稳定性和抗干扰性能。

基于MATLAB的PID模糊控制器的设计与仿真一、模糊控制器的设计步骤(l进行系统分析,确定模糊控制器的输人变量、输出变量及控制器的结构;(2定义输入、输出变量的论域和隶属函数、建立控制规则、确定运算子、选择反模糊化方法;(3模拟试验,可以离线进行仿真试验,也可以在线进行实时测量。

二、MATLAB中的具体操作进入MATLAI3编辑环境后,键人fuzzy即可进人FIS编辑器。

根据题目要求,控制器有两个输入e,de和一个输出u。

在fis编辑器里添加两个输入和一个输出edit-add variable-input/output根据系统实际情况,选择e,de和u的论域e range : [-1 1]de range: [-0.1 0.1]u range: [0 2]e,de和u语言变量的选取e 8个:NB,NM,NS,NZ,PZ,PS,PM,PBde 7个:NB,NM,NS,Z,PS,PM,PBU 7个:NB,NM,NS,Z,PS,PM,PB对de和u按照要求设计成与e相同的样子,根据规则表将55条规则输入到控制器中,点击add rule添加规则。

制定完之后,会形成一个模糊控制规则矩阵,然后根据模糊输入量按照相应的模糊推理算法完成计算,并决策出模糊输出量。

对输出模糊量的解模糊:模糊控制器的输出量是一个模糊集合,通过反模糊化方法判决出一个确切的精确量,凡模糊化方法很多,我们这里选取重心法。

然后Export to disk/workspace,即可得到一个.fis文件,命名为fuzzy这就是你所设计的模糊控制器。

三、仿真验证控制器的设计刚才我们已经完成了对控制的设计,并将它命名为fuzzy,在MATLAB中在用这个控制器之前,需要用readfis指令将fuzzy.fis加载到matlab的工作空间,比如我们用这样的指令:myFLC=readfis(‘fuzzy.fis’;就创建了一个叫myFLC的结构体到工作空间,并在fuzzy logic controller中参数设为:myFLC。