五角星典型零件在Mastercam9.1中的昆氏曲面几何建模
- 格式:pdf
- 大小:107.11 KB
- 文档页数:1



Mastercam9.1的数控编程Mastercam9.1的数控编程引导语:Mastercam9.1数控编程就是利用软件对工件进行几何建模,确定其加工工艺,并选取适当的工艺方法和合理的工艺路线,生成可行的数控刀具路径,自动生成数控代码,并通过计算机仿真验证了加工的正确性。
因此,要学好Mastercam9.1数控编程,就必须多看、多想、多学!到目前为止,你对Mastercam9.1数控编程了解有多少呢?下面看看店铺为大家带来的关于Mastercam9.1数控编程的一些资料,希望这些可以帮助到大家!Mastercam9.1是集计算机辅助设计(CAD)和计算机辅助制造(CAM)于一体的一套完整的数控编程软件,被中小企业及学校广泛采用。
采用Mastercam模拟仿真进行数控实习教学,既解决了学生多数控设备少的矛盾,又能直观逼真地模仿数控设备的整个操作过程,使学生能较快掌握所学专业知识及操作技能,起到事半功倍的作用,教学效果良好。
但是刚开始数控学习的学生,对计算机编程的概念很模糊,一看到都是全新的操作界面更是无从下手。
本文对数控编程部分做一下归纳总结。
一、Mastercam的特点Mastercam的特点是集二维绘图、三维实体造型功能于一身,有比较丰富的CAD功能,加工方式多,有车削、铣削、线切割等加工模块。
在进行二维铣削时,加工方式有外型铣削、挖槽、钻孔、面铣等;在进行三维曲面加工时,又分为粗加工和精加工。
在粗加工和精加工下面又分为若干种加工方法。
灵活选用不同的加工方法,会取得不同的加工效果。
通过设定毛坯和刀具的尺寸,还能完整的模拟整个加工过程。
并且在后置处理库中,可以对生成的程序进行一定的修改,来适应不同的数控机床。
二、Mastercam的编程路径第一,Mastercam9.1的二维铣削加工,加工方式有四种:外型铣削、挖槽、钻孔、面铣等(见图1)。
Contour:二维外型铣削。
Drill:钻孔。
Pocket:二维挖槽。

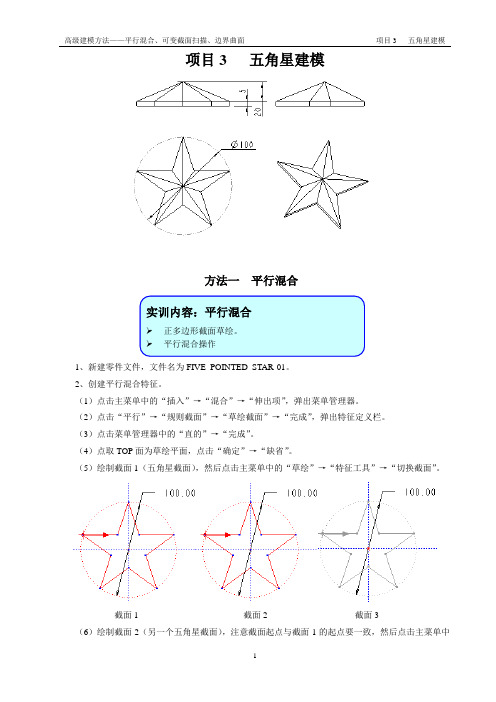
项目3 五角星建模方法一平行混合1、新建零件文件,文件名为FIVE_POINTED_STAR-01。
2、创建平行混合特征。
(1)点击主菜单中的“插入”→“混合”→“伸出项”,弹出菜单管理器。
(2)点击“平行”→“规则截面”→“草绘截面”→“完成”,弹出特征定义栏。
(3)点击菜单管理器中的“直的”→“完成”。
(4)点取TOP面为草绘平面,点击“确定”→“缺省”。
(5)绘制截面1(五角星截面),然后点击主菜单中的“草绘”→“特征工具”→“切换截面”。
截面1 截面2 截面3(6)绘制截面2(另一个五角星截面),注意截面起点与截面1的起点要一致,然后点击主菜单中的“草绘”→“特征工具”→“切换截面”。
(7)绘制截面3(一点),点击草绘截面中的,退出草绘。
(8)输入截面1和截面2的距离为5,截面2和截面3的距离为20. (9)点击定义窗口中的“确定”,完成混合特征建模。
3、重新定义特征,修改特征的属性为“光滑”。
直的光滑思考:1、如何修改截面的起点。
2、也可以先拉伸底板(五角星平板),然后再创建平行混合(只有两个截面,一个五角星截面,另一个是一个点)。
方法二 可变截面扫描1 1、新建零件文件,文件名为FIVE_POINTED_STAR-02。
2、在TOP 面上绘制直线。
3、创建可变截面扫描特征。
(1)点击,弹出扫描特征定义栏。
(2)点击图标(定义扫描特征为实体),在图形点取步骤2中绘制的直线为扫描轨迹(轨迹方向向上),点击定义栏中的“选项”→“可变截面”。
(3)点击图标,进入截面绘制截面,绘制扫描截面(五角星截面),然后点击主菜单中的“工具”→“关系”,弹出“关系”窗口,输入关系“sd3=80-80*trajpar+10*sin(trajpar*360)”,sd3为五角星外接圆的直径。
点击草绘截面中的,退出草绘。
(4)点击特征定义栏中的,完成变截面扫描特征。
思考:修改截面关系式,使图形生成如下。
方法三 可变截面扫描2(园轨迹扫描) 1、新建零件文件,文件名为FIVE_POINTED_STAR-03。

项目4 三维曲面造型4.1 项目描述本项目主要介绍Mastercam X三维曲面造型功能命令的使用,例如拉伸、旋转、扫掠等功能。
通过本项目的学习,完成操作任务——建立图4-1所示的笔筒曲面模型。
图4-1 笔筒曲面模型4.2 项目目标【知识目标】(1)熟悉Mastercam X三维造型的类型;(2)熟悉Mastercam X三维线架模型的构建思路;(3)掌握Mastercam X构图面、视角及构图深度的设置技术;(4)掌握Mastercam X曲面造型功能命令的使用技术。
【技能目标】(1)能综合运用构图面、视角及构图深度,绘制三维线架模型;(2)能综合运用Mastercam X三维曲面造型功能命令,对二维图像进行拉伸、旋转、扫掠等操作来创建各种各样的三维曲面,以及对曲面进行圆角、修剪、曲面融接等操作来构建较为复杂的三维曲面;(3)完成“项目描述”中的操作任务。
4.3 项目相关知识4.3.1 Mastercam X三维造型的类型Mastercam中的三维造型可以分为线架造型、曲面造型以及实体造型三种,这三种造型产生的模型可以从不同角度来描述一个物体。
线架模型用来描述三维对象的轮廓及端面特征,它主要由点、直线、曲面等组成,不具有面和体的特征,不能进行消影、渲染等操作。
曲面模型用来描述曲面的形状,一般是将线架模型经过进一步处理得到的。
曲面模型不仅可以显示出曲面的轮廓,而且可以显示出曲面的真实形状。
各种曲面是由许多的曲面片组成,二这些曲面片又通过多边形网格来定义。
实体造型是使设计者们能在三维空间中建立计算机模型。
实体模型中除包含二维图形数据外,还包括相当多的工程数据,如体积、边界面和边等。
实体模型具有体的特征,可以进行布尔运算等各种体的操作。
4.3.2 构图面、视角及构图深度设置1. 设置构图面在Mastercam中通过构图平面的设置可以将复杂的三维绘图简化为简单的二维绘图。
构图面是指用户进行绘图的平面。
MaterCAM中构建昆氏曲面的技巧
张亚萍
【期刊名称】《泰州职业技术学院学报》
【年(卷),期】2004(004)004
【摘要】MasterCAM中进行计算机辅助设计时常常遇到复杂曲面的造型问题,由于复杂曲面的边界复杂或很不规则,构建比较困难.在直纹曲面、扫描曲面、旋转曲面、昆氏曲面等曲面构建的方法中,昆氏曲面不失为构建复杂曲面的好方法.从昆氏曲面的基本概念、基本框架出发,充分挖掘构建昆氏曲面的条件,阐述了MasterCAM中构建复杂曲面的技巧.
【总页数】4页(P41-44)
【作者】张亚萍
【作者单位】泰州职业技术学院机电系,江苏,泰州,225300
【正文语种】中文
【中图分类】TH16
【相关文献】
1.模具设计中昆氏曲面的构建技巧及后期处理研究 [J], 伍倪燕;廖麟志;陈琪;王海珠
2.MasterCAM中昆氏曲面(Coons)的应用技巧 [J], 高晓东
3.MasterCam X中构建昆氏曲面技巧的研究 [J], 覃羡烘
4.构建复杂昆氏曲面技巧的研究 [J], 刘春利;赵红梅
5.MasterCANI中昆氏曲面的应用技巧 [J], 雷欣荣
因版权原因,仅展示原文概要,查看原文内容请购买。
分解因子法创建MasterCAM昆氏曲面【摘要】:手动创建MasterCAM昆氏(Coons)曲面时,可以采用分解因子法来正确判断曲面引导方向和截断方向的缀面数目,将复杂问题简单化。
【关键词】:分解因子;MasterCAM;昆氏曲面;点;线段;外形;段落MasterCAM昆氏(Coons)曲面是用四条或四条以上边界曲线熔接许多缀面组合形成的一张曲面,其构建方式有两种,即自动串联和手动串联。
对于自动串联比较简单,很好理解,这里笔者不做介绍;而手动串联因涉及到了缀面数目的计算,其计算方法又区分为开放式昆氏曲面缀面数目的计算和封闭式昆氏曲面缀面数目的计算两种,这两种曲面缀面数目的计算所利用的公式又各不一样,所以不少设计员对其感到困难,笔者就手动串联创建昆氏曲面发表自己的新看法。
一、昆氏曲面创建学会转换思维看线段这句话的意思是说我们要将一根线段看作是既可以变长也可以变短的,长到什么程度呢,长到可以由两根或者是两根以上的线段组成;那短呢,则可以短到只有一个点。
下面我们来研究两个具体的昆氏曲面事例。
将上面的图一(三角形ABC)和图二(五边形ABCDE)采用手动串联都创建成为昆氏曲面。
我们现在可以这样来分析,如果是标准的四边形生成昆氏曲面,无论是采用手动还是自动串联都很简单,但是现在是三角形和五边形,所以问题的关键是如何将目前的三角形和五边形与所需要的四边形挂钩。
四边形是由四条边构成,而三角形只有三条边,与四边形相比就少了一条边,我们是否可以将三角形的一个点看作是一条很短的边呢,这样不就是有四条边了吗?同样道理,五边形虽然有五条边,但是我们可以将其中的两条边假设成为一条边。
我们来看创建的过程。
先分析三角形ABC,选择手动生成昆氏曲面,当填写引导方向缀面数和截断方向缀面时都为1(原因后面解释),在提示要求■选择时,要注意两点:一是要求我们要习惯这样来看待这句话“定义引导方向:外形1段落1”,为什么要将这句话反过来读呢,因为我们要强调外形摆在段落的前面;这个软件是由美国CNC Software公司开发的,英语语法习惯和汉语语法习惯不同,这点在信封地址的书写上表现得十分明显,英语要求从小地名写到大地名,而汉语则是从大地名写到小地名,也就是说,这里的外形包含了段落,而不是段落包含了外形(象这样类似的语法习惯在这个软件里面有多处)。