第三章 函数——对数函数学生版
- 格式:docx
- 大小:46.35 KB
- 文档页数:6





3.2.2对数函数【学习要求】1.理解对数函数的概念;2.掌握对数函数的性质;3.了解对数函数在生产实际中的简单应用.【学法指导】通过画函数y=log2x和y=log x的图象,观察其图象特征及由图象归纳函数的性质,进一步培养由特殊到一般、由具体到抽象的思维方法,以及数形结合的数学思想,养成善于观察、归纳的学习习惯.填一填:知识要点、记下疑难点1.对数函数的概念:函数y=log a x (a>0,a≠1,x>0) 叫做对数函数.2.a:(1)对数函数的定义域是正实数集,即(0,+∞) ,值域是实数集R;(2)在定义域内,当a>1 时是增函数, 当0<a<1 时是减函数;(3)图象都通过点(1,0) .研一研:问题探究、课堂更高效探究点一对数函数的概念问题1在现实生活的细胞分裂过程中,细胞个数y是分裂次数x的指数函数y=2x,只要知道了x就能求出y.现在反过来研究,知道了细胞个数,如何确定分裂次数?问题2在问题1得出的关系式中,x是y的函数吗?为什么?问题3我们把函数x=log a y(a>0,a≠1)叫做对数函数,但习惯上自变量用x表示,所以这个函数就写成y=log a x.这样一来,你能给对数函数下一个定义吗?问题4你能说出在指数函数y=2x和对数函数x=log2y中,x,y两个变量之间的相同点及不同点吗?问题5函数y=log a x与函数y=a x(a>0,a≠1)的定义域、值域之间有什么关系?例1求下列函数的定义域(a>0,a≠1):(1)y=log a x2; (2)y=log a(4-x).跟踪训练1求下列函数的定义域(a>0,a≠1):(1)y=log a(9-x2); (2)y=log2(16-4x).探究点二对数函数的图象及性质问题1如何作出函数y=log2x及y=log x的图象?问题2观察作出的函数y=log2x及y=log x的图象,指出这两个函数有哪些相同性质和不同性质?问题3从描出的点及作出的图象中能看出函数y=log2x及y=log 12x的图象的对称关系吗?问题4由具体的函数y =log 2x 及y =log 12x 的性质,你能抽象出对数函数y =log a x (a>0,a≠1,x>0)的哪些性质?探究点三 对数函数性质的应用 例2(1)比较log 23与log 23.5的大小;(2)已知log 0.7(2m)<log 0.7(m -1),求m 的取值范围.跟踪训练2 比较下列各组数中两个值的大小:(1)log 23.4,log 28.5; (2)log 0.31.8,log 0.32.7; (3)log a 5.1,log a 5.9(a>0,a≠1).例3证明:函数f(x)=log 2(x 2+1)在(0,+∞)上是增函数.跟踪训练3求证:函数f(x)=log 2x1-x在(0,1)上是增函数.练一练:当堂检测、目标达成落实处 1.函数y =log 2x -2的定义域是 ( ) A.(3,+∞) B.[3,+∞) C.(4,+∞) D.[4,+∞)2.已知log a <1,那么a 的取值范围是 ( )A.0<a<12B.a>12C.12<a<1D.0<a<12或a>13.函数f(x)=1-2log 6x 的定义域为________.课堂小结:1.在对数函数y =log a x(a>0,且a≠1)中,无论a 取何值,对数函数y =log a x(a>0,且a≠1)的图象均过点(1,0),函数图象落在第一、四象限,且当0<a<1时函数单调递减,当a>1时函数单调递增.2.比较两个(或多个)对数的大小时,一看底数,底数相同的两个对数可直接利用对数函数的单调性来比较大小,若“底”的范围不明确,则需分两种情况讨论;二看真数,底数不同但真数相同的两个对数可借助于图象,或应用换底公式将其转化为同底的对数来比较大小;三找中间值,底数、真数均不相同的两个对数可选择适当的中间值(如1或0等)来比较.。
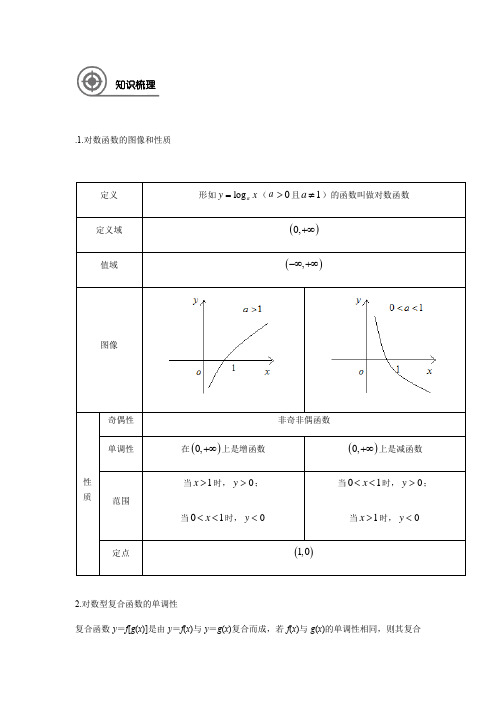
.1.对数函数的图像和性质2.对数型复合函数的单调性复合函数y =f [g (x )]是由y =f (x )与y =g (x )复合而成,若f (x )与g (x )的单调性相同,则其复合定义形如log a y x =(a 0>且1a ≠)的函数叫做对数函数定义域()0,+∞ 值域(),-∞+∞图像性质奇偶性 非奇非偶函数单调性在()0,+∞上是增函数()0,+∞上是减函数范围当1x >时,0y >;当01x <<时,0y < 当01x <<时,0y >;当1x >时,0y <定点 ()1,0知识梳理函数f[g(x)]为增函数;若f(x)与g(x)的单调性相反,则其复合函数f[g(x)]为减函数.对于对数型复合函数y=log a f(x)来说,函数y=log a f(x)可看成是y=log a u与u=f(x)两个简单函数复合而成的,由复合函数单调性“同增异减”的规律即可判断.另外,在求复合函数的单调区间时,首先要考虑函数的定义域.3.数型复合函数的值域对于形如y=log a f(x)(a>0,且a≠1)的复合函数,其值域的求解步骤如下:(1)分解成y=log a u,u=f(x)两个函数;(2)解f(x)>0,求出函数的定义域;(3)求u的取值范围;(4)利用y=log a u的单调性求解.例题解析题型一函数的定义域、值域求含有对数函数的复合函数的定义域、值域,其方法与一般函数的定义域、值域的求法类似,但要注意对数函数本身的性质(如定义域、值域及单调性)在解题中的重要作用.例1求下列函数的定义域:(1); (2).[跟踪训练]1.求下列函数的定义域. (1) y= (2) y=ln(a x-k·2x)(a>0且a ).1[跟踪训练]2.函数y=f(2x)的定义域为[-1,1],求y=f(log2x)的定义域.例2 求下列函数的值域:(1)y=log2(x2+4);(2)y=log1(3+2x-x2).2[跟踪训练]3 函数f(x)=log2(3x+1)的值域为()A.(0,+∞)B.[0,+∞)C.(1,+∞)D.[1,+∞)题型二解对数不等式注意:两类对数不等式的解法(1)形如log a f(x)<log a g(x)的不等式.①当0<a<1时,可转化为f(x)>g(x)>0;①当a>1时,可转化为0<f(x)<g(x).(2)形如log a f(x)<b的不等式可变形为log a f(x)<b=log a a b.①当0<a<1时,可转化为f(x)>a b;①当a>1时,可转化为0<f(x)<a b.例3 已知log0.3(3x)<log0.3(x+1),则x的取值范围为()A.⎝⎛⎭⎫12,+∞B.⎝⎛⎭⎫-∞,12 C.⎝⎛⎭⎫-12,12 D.⎝⎛⎭⎫0,12[跟踪训练]4 不等式log 12(2x +3)<log 12(5x -6)的解集为( )A.(-∞,3)B.⎝⎛⎭⎫-32,3 C.⎝⎛⎭⎫-32,65 D.⎝⎛⎭⎫65,3题型三 对数型复合函数的单调性1.求复合函数单调性的具体步骤是:(1)求定义域;(2)拆分函数;(3)分别求y =f (u ),u =φ(x )的单调性;(4)按“同增异减”得出复合函数的单调性.例4证明函数上是增函数.例5 求函数y =log 0.3(3-2x )的单调区间;例6 讨论函数f(x)=log a(3x2-2x-1)的单调性.[跟踪训练]5 (1)函数f(x)=ln(x2-2x-8)的单调递增区间是()A.(-∞,-2)B.(-∞,1)C.(1,+∞)D.(4,+∞)(3x2-ax+7)在[-1,+∞)上是减函数,求实数a的取值范围.(2)函数f(x)=log13题型四对数型复合函数的奇偶性注意:判断函数的奇偶性时,首先要注意求函数的定义域,函数具有奇偶性,其定义域必须关于原点对称.例7 判断下列函数的奇偶性.(1) (2).例8 已知函数f(x)=log a(x+1)-log a(1-x)(a>0且a≠1).(1)求f(x)的定义域;(2)判断函数f(x)的奇偶性并加以证明.[跟踪训练]6 设函数f(x)=ln(1+x)-ln(1-x),则f(x)是() A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数题型五对数函数的综合应用例9已知函数()()22log 32f x mx mx =-+,m R ∈.(1)若1m =,求函数()f x 的单调递减区间; (2)若函数()f x 的定义域为R ,求实数m 的取值范围.例10已知函数1()log 1axf x x -=+,(0a >且1a ≠). (1)求()f x 的定义域及2(log )f x 的定义域. (2)判断并证明()f x 的奇偶性.例11已知函数()2()log log 2(0,1)a a f x x x a a =-->≠. (1)当2a =时,求(2)f ;(2)求解关于x 的不等式()0f x >;(3)若[2,4],()4x f x ∀∈≥恒成立,求实数a 的取值范围.复合函数y =f [g (x )]及其里层函数μ=g (x )与外层函数y =f (μ)的单调性之间的关系(见下表).函数 单调性y =f (μ) 增函数 增函数 减函数 减函数 μ=g (x ) 增函数 减函数 增函数 减函数 y =f [g (x )]增函数减函数减函数增函数1.思考辨析1. 函数f(x)=ln(x 2−2x −8)的单调递增区间是( )A.B. (−∞,−1)C. (1,+∞)D. (4,+∞)2. 若log a 23<1(a >0,且a ≠1),则实数a 的取值范围是( )A. (0,23)B. (1,+∞)C. (0,23)⋃(1,+∞)D. (23,1)反思总结随堂检测3. 设函数f(x)=log 2(2x −1),则方程f(2x)=f −1(x)的解是( )A. x =1B. x =2C. x =3D. x =44. 已知函数f(x)=log 2(mx 2+mx +1)的值域是R ,则实数m 的取值范围为( )A. 0<m ≤4B. 0≤m ≤4C. m ≥4D. 0≤m <45. 函数y =1−lgx1+lgx (x ≥1)的值域是 ( )A. [−1,1]B. [−1,1)C. (−1,1]D. (−1,1)6. “m ∈{1,2}”是“lnm <1”成立的( )A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件7. 已知,则4a +b 的最小值等于 ( )A. 13B. 15C. 18D. 118. 已知a =log 20.3,b =0.31.3,c =21.3,则a ,b ,c 的大小关系是( )A. a <b <cB. c <a <bC. b <c <aD. b <a <c9. 设a =213,b =log 32,c =cosπ,则( )A. c >b >aB. a >c >bC. c >a >bD. a >b >c10. 已知a =log 25,b =2−0.2,c =0.2−1.2,则( )A. a <b <cB. c <a <bC. b <a <cD. b <c <a11. 已知函数f(x)=(13)x 和函数g(x)=log 13x ,则函数f(x)与g(x)的图象关于( ) A. x 轴对称 B. y 轴对称 C. 原点对称D. 直线y =x 对称12. 已知a >1,函数y =a −x 与y =log a (−x)的图象只可能是()A. B.C. D.13.不等式log0.25(x−1)>1的解集是______.14.给出下列命题: ①直线x=a与函数y=f(x)的图像至少有两个公共点; ②函数y=x−2在(0,+∞)上是单调递减函数; ③幂函数的图像一定经过坐标原点; ④函数f(x)=a x−2(a>0,a≠1)的图像恒过定点(2,1); ⑤设函数y=f(x)存在反函数,且y=f(x)的图像过点(1,2),则函数y=f−1(x)−1的图像一定过点(2,0).其中,真命题的序号为.15.设函数f(x)=lgx,则函数的定义域是__________,若f(2x)>f(2),则实数x的取值范围是__________.16.x1x2分别是方程x+lgx=3和方程x+10x=3的一个根,则x1+x2=______.17.已知函数f(x)=(a2−3a+3)a x是指数函数,(1)求函数f(x)的解析式;(2)判断F(x)=f(x)−f(−x)的奇偶性,并加以证明;(3)解不等式:log a(1−x)>log a(x+2).18.已知函数f(x)=|log a x|(a>0,a≠1).(1)若f(2)=1,求实数a的值;2(2)若0<x1<x2,且f(x1)=f(x2),求x1x2的值;,3]的最大值与最小值之和为2,求实数a的值.(3)若函数f(x)在[1219. 已知函数f(x)=log a x(a >0,a ≠1).(1)若f(a)+f(2a)=3,求实数a 的值;(2)若f(2)>f(3)+2,求实数a 的取值范围.1.设a =20.3,b =0.32,c =log 20.3,则a 、b 、c 的大小关系是( ) A .a <b <c B .b <c <a C .c <b <aD .c <a <b2.函数f (x )=log 12 (x 2-3x -10)的单调递增区间为( )A .(-∞,-2)B .(-∞,32)C .(-2,32)D .(5,+∞) 3.函数f (x )=log a x (0<a <1)在[a 2,a ]上的最大值是( )课后练习A.0B.1C.2D.a4.函数f (x )=log a [(a -1)x +1]在定义域上( ) A.是增函数 B.是减函数 C.先增后减D.先减后增5.已知函数f (x )=ln(1+x 2-x )+1,f (a )=4,则f (-a )=________. 6.讨论函数f (x )=log a (3x 2-2x -1)的单调性.7.已知函数f (x )=log a x +1x -1(a >0,且a ≠1).(1)求f (x )的定义域;(2)判断函数f (x )的奇偶性,并求函数的单调区间.8.若函数y =log a (2-ax )在x ①[0,1]上是减函数,则a 的取值范围是( )A .(0,1)B .(1,2)C .(0,2)D .(1,+∞)9.函数f (x )=lg(1x 2+1+x)是( )A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数 10.设a =log 36,b =log 510,c =log 714,则( ) A.c >b >a B.b >c >a C.a >c >bD.a >b >c11.若定义域为(-2,-1)的函数f (x )=log (2a -3)(x +2),满足f (x )<0,则实数a 的取值范围是________.12.已知函数f (x )=⎩⎪⎨⎪⎧(a -2)x -1,x ≤1,log a x ,x >1,若f (x )在(-∞,+∞)上单调递增,则实数a 的取值范围为________.13..已知f (x )=log 12(x 2-ax +3a )在区间[2,+∞)上为减函数,则实数a 的取值范围是________.14. 已知f (x )=ln 1-mxx -1是奇函数.(1)求m ;(2)判断f (x )在(1,+∞)上的单调性,并加以证明.15.已知函数f(x-1)=lgx 2-x.(1)求函数f(x)的解析式;(2)解关于x的不等式f(x)≥lg(3x+1).。
必修1第三章对数函数的运算法则对数函数是数学中的一种常见函数,它与指数函数是对应关系。
在学习对数函数的运算法则之前,我们先来了解一下对数的定义及其性质。
1.对数的定义:设a为大于0且不等于1的实数,对任意正数x,称满足方程a^y = x的实数y为以a为底x的对数,记作y=log_a(x)。
其中,a称为对数的底数,x称为真数,y称为对数。
2.对数的性质:①对数的底数不为1,大于0,且不等于1② 对数的定义就是一个等式,如果a^b=x,则b=log_a(x)。
③ 对数的值域为全体实数,即:log_a(x)对任何正数x都有定义。
④ 对数函数是一个递增函数,即:当x_1<x_2时,log_a(x_1)<log_a(x_2)。
⑤对数函数的图像关于y轴对称。
⑥ 特殊的对数值:当a>1时,log_a(1)=0;当a<1时,log_a(1)=0。
了解了对数的一些基本概念之后,我们可以来学习对数函数的运算法则了:1.换底公式:log_a(b)=log_c(b)/log_c(a)换底公式是对数运算中的重要公式,它可以将一个对数转化为以另一个底数的对数。
利用这个公式,我们可以在计算对数时灵活选择适用的底数。
2.对数函数的四则运算:①和差公式:log_a(b*c)=log_a(b)+log_a(c);log_a(b/c)=log_a(b)-log_a(c)和差公式可以将对数函数中的乘法和除法转化为加法和减法。
②幂公式:log_a(b^c)=c*log_a(b)幂公式可以将对数函数中的指数转化为乘法。
3.对数函数的指数与对数的互化:指数运算和对数运算是互为逆运算的,即:a^log_a(x)=x;log_a(a^x)=x这个性质在实际运算中经常会用到,可以帮助我们方便地进行对数函数的简化。
4.公式法则:①log_a(b^n)=n*log_a(b);②log_a(b)=log_a(c)+log_c(b);③log_a(b^n)=1/n*log_a(b^);④log_a(x^n)=n*log_a(x);⑤log_a(b)=1/log_b(a)。
第2课时 对数的运算性质及换底公式1.了解对数的换底公式.2.理解对数的运算性质.3.掌握用对数的运算性质进行化简与证明.[学生用书P49]1.如果a >0,且a ≠1,M >0,N >0,那么 (1)log a (MN )=log a M +log a N ; (2)log a M N=log a M -log a N ; (3)log a M n=n log a M (n ∈R ). 2.换底公式一般地,称log a N =log c Nlog c a(a >0且a ≠1,c >0且c ≠1,N >0)为对数的换底公式.1.判断(正确的打“√”,错误的打“×”)(1)两个正数的积、商的对数可以化为这两个正数的对数的和、差.( ) (2)log a (xy )=log a x ·log a y .( ) (3)log 2(-5)2=2log 2(-5).( ) (4)由换底公式可得log a b =log (-2)blog (-2)a.( )答案:(1)√ (2)× (3)× (4)×2.已知a >0且a ≠1,则log a 2+log a 12=( )A .0B .12 C .1 D .2答案:A3.(1)lg 10=________;(2)已知ln a =0.2,则ln ea=________.答案:(1)12(2)0.84.log 29log 23=________. 答案:2对数的运算性质及应用[学生用书P49]计算下列各式:(1)12lg 3249-43lg 8+lg 245; (2)2lg 2+lg 31+12lg 0.36+13lg 8;(3)lg 25+23lg 8+lg 5lg 20+(lg 2)2.【解】 (1)原式=12(5lg 2-2lg 7)-43×32lg 2+12(2lg 7+lg 5)=52lg 2-lg 7-2lg 2+lg 7+12lg 5 =12lg 2+12lg 5=12(lg 2+lg 5)=12lg 10=12. (2)2lg 2+lg 31+12lg 0.36+13lg 8=lg 4+lg 31+lg 0.6+lg 2=lg 12lg (10×0.6×2)=lg 12lg 12=1.(3)原式=2lg 5+2lg 2+(1-lg 2)(1+lg 2)+(lg 2)2=2(lg 5+lg 2)+1-(lg 2)2+(lg 2)2=2+1=3.(1)对于同底的对数的化简,常用的方法是:①“收”,将同底的两对数的和(差)收成积(商)的对数(逆用运算性质); ②“拆”,将积(商)的对数拆成对数的和(差)(正用运算性质).(2)对数式的化简,求值一般是正用或逆用公式.要养成正用、逆用、变形应用公式的习惯,lg 2+lg 5=1在计算对数值时会经常用到,同时注意各部分变形要化到最简形式.1.计算下列各式:(1)12lg 25+lg 2+lg 10+lg(0.01)-1;(2)2log 32-log 3329+log 38-3log 55.解:(1)法一:原式=lg[2512×2×1012×(10-2)-1] =lg (5×2×1012×102) =lg 1072=72.法二:原式=12lg 52+lg 2+12lg 10-lg 10-2=(lg 5+lg 2)+12-(-2)=lg 10+12+2=1+12+2=72.(2)法一:原式=log 322+log 3(32×2-5)+log 323-3 =log 3(22×32×2-5×23)-3 =log 332-3 =2-3=-1.法二:原式=2log 32-()5log 32-2+3log 32-3 =2-3=-1.换底公式的应用[学生用书P50](1)计算:(log 2125+log 425+log 85)·(log 52+log 254+log 1258); (2)已知log 189=a ,18b=5,求log 3645(用a ,b 表示). 【解】 (1)法一:原式=⎝⎛⎭⎪⎫log 253+log 225log 24+log 25log 28⎝ ⎛⎭⎪⎫log 52+log 54log 525+log 58log 5125 =⎝⎛⎭⎪⎫3log 25+2log 252log 22+log 253log 22⎝ ⎛⎭⎪⎫log 52+2log 522log 55+3log 523log 55 =⎝ ⎛⎭⎪⎫3+1+13log 25·(3log 52)=13log 25·log 22log 25=13. 法二:原式 =⎝ ⎛⎭⎪⎫lg 125lg 2+lg 25lg 4+lg 5lg 8⎝ ⎛⎭⎪⎫lg 2lg 5+lg 4lg 25+lg 8lg 125=⎝⎛⎭⎪⎫3lg 5lg 2+2lg 52lg 2+lg 53lg 2⎝ ⎛⎭⎪⎫lg 2lg 5+2lg 22lg 5+3lg 23lg 5=⎝⎛⎭⎪⎫13lg 53lg 2⎝ ⎛⎭⎪⎫3lg 2lg 5=13.(2)法一:因为18b=5,所以log 185=b , 又log 189=a ,于是log 3645=log 1845log 1836=log 18(9×5)log 18(18×2)=log 189+log 1851+log 182=a +b 1+log 18189=a +b 2-a.法二:因为log 189=a ,18b=5,所以lg 9=a lg 18, lg 5=b lg 18,所以log 3645=lg 45lg 36=lg (9×5)lg 1829=lg 9+lg 52lg 18-lg 9=a lg 18+b lg 182lg 18-a lg 18=a +b2-a.法三:因为log 189=a ,所以18a=9. 又因为18b=5,所以45=5×9=18b·18a=18a +b.令log 3645=x ,则36x=45=18a +b,即36x=⎝ ⎛⎭⎪⎫183·183x=18a +b.所以⎝ ⎛⎭⎪⎫1829x=18a +b,所以x log 181829=a +b ,所以x =a +b log 18182-log 189=a +b 2-a ,即log 3645=a +b2-a.(1)具有换底功能的另两个结论:①log a c ·log c a =1,②log an b n=log a b .(a >0且a ≠1,b >0,c >0且c ≠1)(2)求条件对数式的值,可从条件入手,从条件中分化出要求的对数式,进行求值;也可以从结论入手,转化成能使用条件的形式;还可同时化简条件和结论,直至找到它们之间的联系.(3)本题主要考查已知一些指数值或对数值,利用这些条件来表示所要求的式子,解决该类问题必须熟练掌握所学性质和法则,并学会运用整体思想.2.(1)计算:(log 43+log 83)log 32=________.(2)计算:log22+log 279=________.解析:(1)原式=⎝ ⎛⎭⎪⎫1log 34+1log 38log 32=⎝⎛⎭⎪⎫12log 32+13log 32log 32=12+13=56.(2)原式=log 22log 2212+log 332log 333=112+23=2+23=83.答案:(1)56 (2)83对数的综合应用[学生用书P50]若a ,b 是方程2(lg x )2-lg x 4+1=0的两个实根,求lg(ab )·(log a b +log b a )的值. 【解】 原方程可化为2(lg x )2-4lg x +1=0, 设t =lg x ,则原方程可化为2t 2-4t +1=0.所以t 1+t 2=2,t 1t 2=12.由已知a ,b 是原方程的两个根,则t 1=lg a ,t 2=lg b ,即lg a +lg b =2,lg a ·lg b =12,所以lg(ab )·(log a b +log b a ) =(lg a +lg b )⎝⎛⎭⎪⎫lg b lg a +lg a lg b=(lg a +lg b )[(lg b )2+(lg a )2]lg a lg b=(lg a +lg b )·(lg b +lg a )2-2lg a lg blg a lg b=2×22-2×1212=12.即lg(ab )·(log a b +log b a )=12.应用对数的运算性质解对数方程的三种方法(1)定义法:解形如b =log a f (x )(a >0,a ≠1)的方程时,常借助对数函数的定义等价转化为f (x )=a b 求解.(2)转化法:形如log a f (x )=log a g (x )(a >0,a ≠1)的方程,等价转化为f (x )=g (x ),且⎩⎪⎨⎪⎧f (x )>0,g (x )>0求解. (3)换元法:适用于f (log a x )=0(a >0,a ≠1)形式的方程的求解问题,这类方程一般可通过设中间变量的方法(换元法)来解.3.(1)方程log 4(3x -1)=log 4(x -1)+log 4(x +3)的解为________.(2)已知lg(x +2y )+lg(x -y )=lg 2+lg x +lg y ,求x y的值. 解:(1)原方程可化为3x -1=(x -1)(x +3), 即x 2-x -2=0, 解得x =2或x =-1,而x =-1使真数3x -1和x -1小于0, 故方程的解是x =2.故填x =2. (2)由已知条件得⎩⎪⎨⎪⎧x +2y >0,x -y >0,x >0,y >0,(x +2y )(x -y )=2xy ,即⎩⎪⎨⎪⎧x >y ,y >0,(x +2y )(x -y )=2xy ,整理得⎩⎪⎨⎪⎧x >y ,y >0,(x -2y )(x +y )=0,所以x -2y =0,所以xy=2.1.对对数的运算性质的理解(1)利用对数的运算性质可以把求正数的乘、除、乘方的对数的运算转化为这些正数的对数的加、减、乘运算,反之亦然.但两个正数的和或差的对数没有运算性质.(2)对于每一条运算性质,都要注意只有当式子中所有的对数都有意义时,等式才成立. (3)能用语言准确叙述对数的运算性质log a (M ·N )=log a M +log a N →积的对数等于对数的和. log a M N=log a M -log a N →商的对数等于对数的差.log a M n=n log a M (n ∈R )→真数的n 次幂的对数等于对数的n 倍. 2.关于换底公式的两点说明(1)换底公式成立的条件是公式中的每一个对数式都有意义.(2)利用换底公式,可以“随意”地改变对数的底,应注意选择适当的底数,一般转化为常用对数或自然对数,化简和证明中常常用到换底公式.已知lg a +lg b =2lg(a -2b ),求log 2a b的值. [解] 因为lg a +lg b =2lg(a -2b ), 所以lg ab =lg(a -2b )2,ab =(a -2b )2,a 2-5ab +4b 2=0,即(a -b )(a -4b )=0, 所以a =b 或a =4b . 又因为a -2b >0,所以a =4b ,log 2a b=log 24=2.(1)错因:易忽视真数大于0的限制,导致出现增解. (2)防范:将对数化简、变形,不能忘记真数大于0的限制.1.化简12log 612-2log 62的结果为( )A .6 2B .12 2C .log 6 3D .12 解析:选C.原式=log 612-log 62=log 6122=log 6 3. 2.已知a =log 32,那么log 38-2log 36用a 表示是( ) A .a -2 B .5a -2 C .3a -(1+a )2D .3a -a 2解析:选A.log 38-2log 36=3log 32-2(log 32+1)=log 32-2=a -2. 3.(1)log 52·log 79log 513·log 734=________.(2)log 2()3+5- 3-5=________.解析:(1)原式=log 132·log 349=12lg 2-lg 3·2lg 323lg 2=-32.(2)原式=12log 2(3+5- 3-5)2=12log 2[](3+5)+(3-5)-2(3+5)(3-5) =12log 2(6-4) =12log 22=12. 答案:(1)-32 (2)124.用lg x ,lg y ,lg z 表示下列各式:(1)lg(xyz ); (2)lg xy 2z ;(3)lg xy 3z; (4)lg x y 2z .解:(1)lg(xyz )=lg x +lg y +lg z ;(2)lg xy 2z =lg(xy 2)-lg z =lg x +2lg y -lg z ;(3)lg xy 3z=lg(xy 3)-lg z=lg x +3lg y -12lg z ;(4)lgx y 2z=lg x -lg(y 2z ) =12lg x -2lg y -lg z . [学生用书P111(单独成册)])[A 基础达标]1.lg 8+3lg 5的值为( ) A .-3 B .-1 C .1D .3解析:选D.lg 8+3lg 5=lg 8+lg125=lg1 000=3. 2.设log 34·log 48·log 8m =log 416,则m 的值为( ) A.12B .9C .18D .27解析:选B.由题意得lg 4lg 3·lg 8lg 4·lg mlg 8=log 416=log 442=2, 所以lg m lg 3=2,即lg m =2lg 3=lg 9. 所以m =9,选B.3.若lg x =m ,lg y =n ,则lg x -lg ⎝ ⎛⎭⎪⎫y 102的值为( ) A.12m -2n -2 B .12m -2n -1 C.12m -2n +1 D .12m -2n +2 解析:选D.因为lg x =m ,lg y =n ,所以lg x -lg ⎝ ⎛⎭⎪⎫y 102=12lg x -2lg y +2=12m -2n +2.故选D.4.设lg 2=a ,lg 3=b ,则log 512等于( ) A.2a +b1+a B .a +2b1+a C.2a +b 1-aD .a +2b1-a解析:选C.log 512=lg 12lg 5=lg (22×3)lg (10÷2)=lg 22+lg 3lg 10-lg 2=2lg 2+lg 31-lg 2=2a +b1-a .故选C.5.已知2x=3,log 483=y ,则x +2y 等于( )A .3B .8C .4D .log 48解析:选A.因为2x=3,所以x =log 23. 又log 483=y ,所以x +2y =log 23+2log 483=log 23+2(log 48-log 43)=log 23+2⎝ ⎛⎭⎪⎫32log 22-12log 23 =log 23+3-log 23=3.故选A.6.已知m >0,且10x=lg(10m )+lg 1m,则x =________.解析:lg(10m )+lg 1m =lg 10+lg m +lg 1m=1,所以10x =1=100.所以x =0. 答案:07.方程log 3(x 2-10)=1+log 3x 的解是________.解析:原方程可化为log 3(x 2-10)=log 3(3x ),所以x 2-10=3x ,解得x =-2,或x =5.经检验知x =5.答案:x =58.已知2m =3n=36,则1m +1n=________.解析:m =log 236,n =log 336,所以1m =log 362,1n =log 363,所以1m +1n =log 366=12.答案:129.计算下列各式:(1)lg 8+log 39+lg 125+log 319;(2)[log 2(log 216)](2log 36-log 34);(3)⎝ ⎛⎭⎪⎫lg 4-lg 60lg 3+lg 53-45×2-11. 解:(1)原式=lg 8+lg 125+log 39+log 319=lg(8×125)+log 3⎝ ⎛⎭⎪⎫9×19=lg 1 000+log 31=3+0=3. (2)原式=(log 24)(log 336-log 34)=2log 3364=2log 39=4.(3)原式=⎝ ⎛⎭⎪⎪⎫lg 460lg 153-210×2-11=⎝ ⎛⎭⎪⎫-lg 15lg 153-2-1 =-1-12=-32.10.解下列关于x 的方程: (1)lg x -1=lg(x -1);(2)log 4(3-x )+log 0.25(3+x )=log 4(1-x )+log 0.25(2x +1).解:(1)原方程等价于⎩⎨⎧x -1=x -1,x -1>0.解之得x =2. 经检验x =2是原方程的解,所以原方程的解为x =2.(2)原方程可化为log 4(3-x )-log 4(3+x )=log 4(1-x )-log 4(2x +1).即log 43-x 3+x=log 41-x 2x +1. 整理得3-x x +3=1-x 2x +1,解之得x =7或x =0. 当x =7时,3-x <0,不满足真数大于0的条件,故舍去.x =0满足,所以原方程的解为x =0.[B 能力提升]1.若log 513·log 36·log 6x =2,则x 等于________. 解析:由换底公式,得-lg 3lg 5·lg 6lg 3·lg x lg 6=2, lg x =-2lg 5,x =5-2=125. 答案:1252.计算log 8(log 242)的值为________.解析:log 8(log 242)=log 814=-2log 82=-23. 答案:-233.若log a b +3log b a =132,则用a 表示b 的式子是________. 解析:原式可化为1log b a +3log b a =132, 整理得3(log b a )2+1-132log b a =0, 即6(log b a )2-13log b a +2=0;解得log b a =2或log b a =16, 所以b 2=a 或b 16=a , 即b =a 或b =a 6.答案: b =a 或b =a 64.(选做题)已知地震的震级R 与地震释放的能量E 的关系为R =23(lg E -11.4).若A 地地震级别为9.0级,B 地地震级别为8.0级,求A 地地震释放的能量是B 地地震释放的能量的多少倍.解:由R =23(lg E -11.4), 得32R +11.4=lg E , 故E =10(32R +11.4).设A 地和B 地地震释放的能量分别为E 1,E 2,则E 1E 2=10(32×9.0+11.4)10(32×8.0+11.4)=1010, 即A 地地震释放的能量是B 地地震释放的能量的1010倍.。
必修1第三章对数函数的运算法则(全)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(必修1第三章对数函数的运算法则(全))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为必修1第三章对数函数的运算法则(全)的全部内容。
【本讲教育信息】一. 教学内容:对数运算、对数函数二. 重点、难点:1. 对数运算,0,1,1,0,0>>≠≠>>N M b a b a (1)x N a =log Na x =⇔(2)01log =a (3)1log =a a (4)Na N a=log (5)NM N M a a a log log )(log +=⋅(6)N M NM a a a log log log -=(7)M x M a x a log log ⋅=(8)aM M b b a log /log log =(9)b xy b a y a xlog log =(10)1log log =⋅a b b a 2. 对数函数,且x y a log =0>a 1≠a 定义域()+∞,0值域R单调性 ↓∈)1,0(a ↑+∞∈),1(a 奇偶性非奇非偶过定点(1,0)图象与关于轴对称x y a log =x y a1log =x【典型例题】[例1] 求值(1) ;=7log391((2) ;=-++4log 20log 23log 2log 15151515(3) ;=+⋅+18log 3log 2log )2(log 66626(4) ;=⋅81log 16log 329(5) ;=+⋅++)2log 2(log )5log 5)(log 3log 3(log 2559384(6) .=+⋅+2)2(lg 50lg 2lg 25lg 解:(1)原式491733)3(27log 7log 27log 22333=====----(2)原式115log 15==(3)原式18log )3log 2(log 2log 6666++⋅= 236log 18log 2log 666==+=(4)原式58)3log 54()2log 24(23=⋅=(5)原式815)2log 23()5log 23()3log 65(532=⋅⋅=(6)原式)2lg 50(lg 2lg 25lg ++= 2100lg 2lg 225lg ==+=[例2] 若满足z y x ,,)](log [log log )](log [log log 33132212y x =)]z (log [log log 5515=,试比较的大小关系.0=z y x 、、解:log 2〔log (log 2x )〕=0log (log 2x )=1log 2x =x ==(215)。