包装中的数学的数学问题(20200730170648)

“包装中的数学问题”教学设计活动目标：1、通过实践，能利用表面积等相关知识，探究相同的长方体叠放的方法及使其表面积最小的最优策略，体验策略的多样化，发展优化思想。

2、通过观察、操作、比较、分析等过程，体验解决问题的基本过程和方法，自主发现规律，并能应用规律解决实际问题，提高解决问题的能力，同时进一步体会面、棱、体之间的关系，进一步培养学生的空间感。

3、在活动过程中，培养创新意识和实践操作能力，感受数学与生活的密切联系。

教学重点：进一步体会面、棱、体之间的关系，进一步培养学生的空间感教学难点：体验解决问题的基本过程和方法教学过程：一、精彩两分钟——长方体中的拼与合师：感谢xxx给我们带来的精彩两分钟，通过她拿着教具，边操作边解说，让我们把长方体中的分与合看得一清二楚！因此以后的学习中，我们也要多借助模型来帮助我们思考！二、引入新课：师：这段时间我们一直在研究关于长正方体的知识，今天我们一起来研究——包装中的数学问题。

提到包装，我们并不陌生，请看大屏幕——（这是两种牛奶的包装、纸巾的包装以及香烟的包装等等）看到这些包装，我想问问同学们，如果你是一个包装公司的经理，你会考虑哪些问题？预设：生：要美观、方便、降低成本、多赚钱、省材料师：对，这些都是包装公司经理要考虑的！而最能给经理省钱的就是节省材料！节约了成本，经理才能多获利！今天我们就来研究“相同的长方体怎样摆放，才能使包装箱的材料最节省？”（一）说研究方法：1、我们以这种长方体的香皂盒为例来研究（贴在黑板上），课前我们测量过它的长是9.7厘米，宽6厘米，高3.5厘米。

为了方便研究，我们这样取整，长≈10厘米，宽=6厘米，高≈3厘米。

（标注在黑板上）现在要把这样的6块香皂放在一个大包装箱里。

请你设计一种大包装箱，并让这种包装箱最省材料。

（重叠处的面积忽略不计）2、谁说说你打算怎么研究？预设：生：先有序的摆出所有的摆法。

师：怎样做到有序？生：大面重合、中面重合、小面重合、大中面重合、大小面重合、中小面重合再记录每种摆法的长宽高并计算出每种摆法的表面积。

综合实践活动教学设计包装中的数学问题一、主题内容设计：我授课的内容是五年级下册长方体表面积的运用，通过与生活紧密联系的实践活动，培养学生综合运用长方体等相关知识解决实际问题的能力，使学生在实践、操作、探索中感受优化思想、形成数学思考，增强空间观念和节约意识。

学生已经掌握了长方体、正方体的特征，表面积的计算，对一些组合图形有了一定的认识，能根据要求合并、分割简单的正方体和长方体，具备初步的猜测归纳能力。

但是，对于复合立体图形的组合问题接受还可能存在困难，要借助实物操作、观察比较，帮助学生建立空间观念。

在这个操作、探究、合作、分享的过程中，使学生感受数学知识与生活是密不可分的，培养学生的探索意识和创新精神，“为培养具有中国底蕴、国际视野的社会主义的建设者和接班人奠基”。

二、主题活动目标设计：1.学生能够利用表面积等相关知识，探索相同的长方体叠放的方法及使其表面积最小的最优策略。

2.采用问题解决的教学模式，引导学生开展自主探究、合作交流的教学活动，培养学生小组合作、沟通交流能力。

3.学生体会数学在日常生活和生产中的作用和价值，增强学生应用数学的意识，继承中华民族勤俭节约的传统美德。

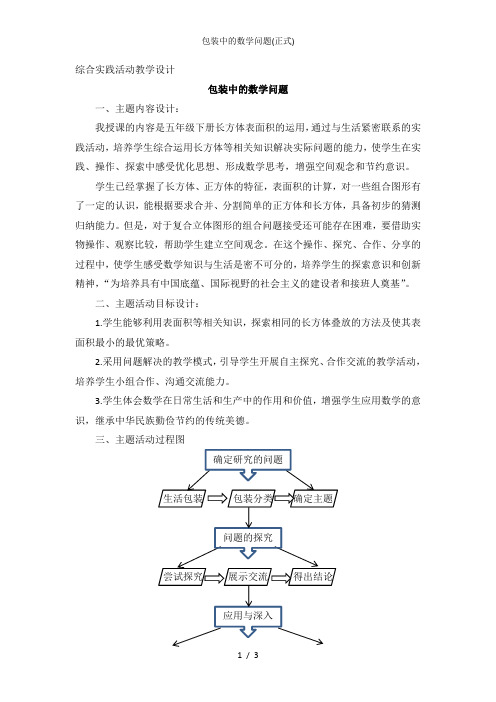
三、主题活动过程图应用结论数学与生活密不可分四、主题活动过程：（一）确定研究的问题1、同学们，上课之前我们先来看一组咱们大家搜集的图片。

（出示生活中的包装图片）2、你们看这些包装图片有什么不一样吗？（学生说说自己想法）那么，今天我们就来当一次肥皂厂的小职工，一起来研究如何节约包装材料的包装问题。

（二）问题的探究1、咱们的工厂接到一个订单，要将我们的肥皂每两块包装在一起进行销售，要想最节约成本，请你设计一种包装方案。

每个人先想一想，可以怎样包装？2、小组合作：①动手摆一摆，试试可以有几种不同的组合方法；②尝试判断哪种方案最节约包装纸。

3、小组展示成果，说一说每种组合方法隐藏了几个面。

得出结论：隐藏的面积越大，组合后的长方体表面积越小。

1包装中的数学问题万君教学内容：小学数学五年级下册“包装中的数学问题”教材分析：本课教学内容是在学生掌握了长方体特征及表面积计算等相关知识的基础上，进一步探究几个相同长方体组合成新长方体的多种方案以及使其表面积最小的最优策略。

教材把这部分知识安排在第一单元“长方体和正方体”后，主要意图是通过这样一系列与生活紧密联系的实践活动，培养学生综合应用所学的知识解决实际问题的能力。

在这系列实践活动中，主要涉及数与代数、空间与图形两部分知识，在解决生活实际问题的过程中，分别培养了学生的估算意识、计算中的最优策略以及组合立体图形的表面积最优策略。

包装问题在日常生活中经常遇到，教材创设“包装”的情景，使学生综合应用表面积等知识来讨论如何节约包装纸的问题，它不仅培养学生的节约意识，更体现了数学的优化思想。

同时有助于培养学生空间感，提高解决实际问题的能力，感受数学与实际生活的密切联系。

学生情况分析：1、学生已有的知识基础：在本课学习之前，学生已熟练掌握了长方体、正方体的特征，能准确、迅速的计算出单一物体的棱长、表面积、体积，能把几个相同的正方体组合成新的正方体。

初步接触了由两个相同的正方体拼成一个长方体后表面积发生的变化。

2、学生已有的生活经验：多数学生得到过生日礼物，也曾经为同伴或家人准备过礼物，接触过礼品的包装，知道包装纸的大小不仅与价格有关，也能清楚地意识到用包装纸包装起来的部分就是物体的表面积。

3、学生学习本课内容可能遇到的困难及学习方式的研究：学生在探究由4个至多个相同的长方体组合成新的长方体时，对于方法的多样化与策略的最优化可能存在问题，通过动手操作大多数学生可以得到由4个相同长方体组合成新的长方体时的六种拼摆方法，但思维无序，对于方法的归纳和总结存在2困难，因此以小组合作的活动方式进行研究，同伴之间相互补充，共同归纳总结，有助于培养学生的思维的有序性。

小组合作的学习方式应当是本课内容的最佳路径，学生可以在小组学习中充分体现解决拼摆方法的多样化，对于策略的最优化，存在更大的困难，这时需要教师发挥引导作用，带领全班学生通过比较六种拼摆、叠放方法，得到最相近的两种方法（即六个大面重叠或四个大面四个中面重叠），引发争论，再让学生通过观察实物、计算、说理推导、比较数值等多种方法结合具体事物，得到最优策略。

包装里的数学问题可以是一个广泛而复杂的主题，涉及许多不同的方面和层次。

下面我将尝试概述一个具体的包装问题的描述和解决方案，以便更深入地探讨包装中的数学问题。

首先，我们需要考虑包装的本质。

包装是一个涉及到空间、形状、质量和尺寸的问题。

一个简单的包装问题可能涉及到将一系列不同形状和尺寸的物品装入一个容器中，以确保所有物品都被正确放置且不相互挤压或溢出容器。

这种问题的解决涉及到数学几何学、数学运筹学和统计学的应用。

为了说明这个问题，让我们考虑一个特定的例子。

假设有一组由各种大小和形状的圆罐和方罐组成的物品，我们需要找到一种包装方法，使得所有的物品都尽可能紧密地排列在一起，并且不会发生重叠或遗漏。

这是一个典型的“装箱问题”，可以使用数学方法进行优化。

一种可能的解决方案是使用数学优化算法，如遗传算法或模拟退火算法。

这些算法可以在搜索空间中找到最优解，通过不断尝试不同的包装方案并评估其性能，最终找到满足所有约束条件的最佳解决方案。

在解决这个问题时，我们需要考虑一些关键因素，如物品的数量、每个物品的尺寸和质量、容器的尺寸和形状、以及约束条件（如每个物品都必须被包含在内，不能有任何物品被挤压或溢出容器）。

通过将这些因素纳入考虑范围，我们可以使用数学模型来建立包装问题的数学模型，并使用优化算法来求解。

此外，我们还可以考虑一些更复杂的因素，如物品的随机性、容器的可变性等。

在这种情况下，我们可以使用概率和统计方法来建模和解决问题。

例如，我们可以考虑一些随机因素（如物品的随机大小或随机放置）对包装方案的影响，并使用概率模型来评估这些因素对最终解决方案的影响。

总之，包装中的数学问题是一个涉及空间、形状、质量和尺寸的复杂问题，需要使用数学方法进行建模和优化。

通过使用数学优化算法和概率和统计方法，我们可以找到最优的包装方案，并确保所有物品都被正确放置且不相互挤压或溢出容器。

这不仅是一个实用的应用，也是数学在现实生活中的应用之一，展示了数学在解决实际问题中的重要性和价值。