数学北师大版五年级下册包装的问题

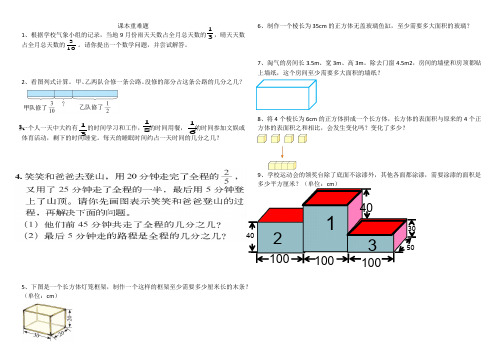
31103618131课本重难题 1、根据学校气象小组的记录，当地9月份雨天天数占全月总天数的 ，晴天天数占全月总天数的 。

请你提出一个数学问题，并尝试解答。

2、看图列式计算。

甲、乙两队合修一条公路。

没修的部分占这条公路的几分之几？ 一个人一天中大约有 的时间学习和工作， 的时间用餐， 的时间参加文娱或体育活动，剩下的时间睡觉。

每天的睡眠时间约占一天时间的几分之几？5、下图是一个长方体灯笼框架，制作一个这样的框架至少需要多少厘米长的木条？（单位：cm ）6、制作一个棱长为35cm 的正方体无盖玻璃鱼缸，至少需要多大面积的玻璃？7、淘气的房间长3.5m 、宽3m 、高3m 。

除去门窗4.5m2，房间的墙壁和房顶都贴上墙纸，这个房间至少需要多大面积的墙纸？8、将4个棱长为6cm 的正方体拼成一个长方体，长方体的表面积与原来的4个正方体的表面积之和相比，会发生变化吗？变化了多少？9、学校运动会的领奖台除了底面不涂漆外，其他各面都涂漆，需要涂漆的面积是多少平方厘米？（单位：cm ）3、 30 250 4040131001001002110、爸爸和乐乐都感冒了妈妈要给他们买3天的药。

⑴爸爸和乐乐一天分别要吃多少袋？ ⑵妈妈总共需要买多少袋药？11、12、某种松鼠的体长在20cm 到28cm 之间，它的尾巴约占体长的 ，尾巴最长约有多长？最短约有多长？13、一个长方体水池，底面长12dm ，宽6dm 。

如果要向这个池子里注入2dm 高的水，需要多少升水？14、牙膏盒长15cm ，宽和高都是3cm 。

现有一纸箱， 内侧的尺寸如图（单位：cm ）。

这个纸箱中最多能放多少盒牙膏？与同伴交流，说一说你是怎么 想的。

15、将一个长8cm 、宽5cm 、高3cm 的长方体截成一个体积最大的正方体，这个正方体的体积是多少？结合下边的图想一想，再算一算。

（单位：cm ） 16、棱长为2m 的正方体盒子，可以放多少个棱长为2dm 的小正方体？17、购买那种包装的牛奶比较合算？18、一个长方体容器，底面长2dm 、宽1.5dm ，放入一个土豆后水面升高了0.2dm ，这个土豆的体积是多少？19、将2个西红柿浸没在盛了250mL 水的量杯后，水位上升至600mL ，平均每个西红柿的体积是多少立 方厘米？20、一只蚂蚁15秒爬了 109dm ，平均每秒爬多少分米？21、一瓶果酱有 kg ，淘气家5天吃完，平均每天吃多少千克？相当于多少克？22、分一分，算一算。

北师大版五年级数学下册《应用题》练习题（含答案）1．万老师把516m长的木棒锯成相等的若干段，共锯了4次，每段长多少米？2．一个正方体无盖木箱棱长8分米，做这个木箱至少需要多少平方分米木板？木箱的体积是多少立方分米？3．将2个西红柿浸没在盛了250毫升水的量后，水位上升至600毫升，平均每个西红柿的体积是多少立方厘米？4．把一条4m长的绳子截成14m长的小段，可以截成多少段，共需要截几次？5．一袋花生米45kg，吃去了14，这袋花生米还剩多少kg？6．甲跑步时测得每分钟心跳是126次，跑步结束休息后心跳恢复正常，每分钟心跳次数是跑步时的59。

甲的心跳恢复正常后是每分钟多少次？7．用棱长1cm的小正方形摆成一个长8cm，宽和高都是3cm的长方体，需要用多少个小正方体？长方体的体积是多少？8．一种礼品盒(如图)长30厘米，宽25厘米，高20厘米．如果要用红丝线把它捆扎起来，结头处丝线留出30厘米，至少需要多少米丝线？9．永盛商场2016年下半年空调和冰箱销售台数如下：（1）根据上表中的数据制成折线统计图。

永盛商场2016年下半年空调和冰箱销售情况统计图（2）回答以下问题。

①空调________月销售量最高，是________台；________月销售量最低，是________台；冰箱________月销售量最高，是________台，________月销售量最低，是________台。

②________月冰箱和空调的销售量相差最大，________月冰箱和空调的销售量相差最小。

（3）如果每台冰箱获利100元，那么这个商场电器城2016年下半年冰箱销售中共获利多少元？10．尚老师要测量乒乓球的体积，可是乒乓球浮在水面上，不能浸在水中，请给尚老师想个办法，怎样才能测量出乒乓球的体积？11．王师傅做了一个玻璃鱼缸，这个鱼缸的容积和体积一样大吗？12．一个西瓜，亮亮吃了这个西瓜的16，爸爸吃了这个西瓜的14，爸爸比亮亮多吃这个西瓜的几分之几？13．甲、乙、丙三个数，甲与乙的平均数是84，乙与丙的平均数是92，乙数是85。

北师大版五年级小学数学下册应用题(40题)及解析答案一、北师大小学数学解决问题五年级下册应用题1．张华买了一批菜油，放在A，B两个桶里，两个桶都未能装满。

如果把A桶油倒入B桶后，B桶装满，A桶还剩10升菜油；如果把B桶油倒入A桶后，A桶还要再加20升菜油才满。

已知A桶容量是B桶的2.5倍。

问：张华一共买了多少升菜油？2．先认真阅读下面的背景资料再根据信息完成问题。

幸福小区里有个为民超市，超市房间从里面量长8米，宽5.6米，高3米，门窗面积共5.2平方米。

超市收银台旁有一个长6分米，宽5分米，高4分米的长方体鱼缸。

新冠肺炎疫情得到控制后，今年5月，超市进行了重新装修：房间的四壁和房顶贴上了新的墙纸，地面重新铺了正方形的地板砖，鱼缸（无盖）的棱上贴上了装饰条儿，鱼缸还放了美丽的珊瑚……6月1日超市重新开业，购进大量的商品，其中有很多小朋友爱喝的饮料，还有一些大米和80桶食用油。

（1）装修时至少用了多大面积的墙纸（门窗不贴墙纸）？（2）如果用边长8分米，每块单价为108元的地砖来铺地，一共需要多少钱？3．某公司订购400根方木，每根方木横截面的面积是25平方分米，长是4米，这些木料一共有多少方？（1方=1立方米）4．将小正方体按下图靠墙摆放。

小正方体的个数24681012…2a露在外面的面的个数5．水果店运来一批水果，其中香蕉360千克，菠萝的质量是香蕉的，橘子的质量比菠萝的少15千克。

水果店运来橘子多少千克？（先画线段图分析数量关系，再列式计算）6．小华的妈妈买了香蕉和苹果各2kg，共花了14.4元．如果香蕉的价钱是苹果的1.25倍，每千克香蕉和苹果各多少元？（用方程解答）7．同学们摘桃子，一班比二班多摘28千克，一班有52人，平均每人摘4千克，二班有50人，平均每人摘多少千克？（列方程解答）8．你能把宣传栏上破损的数补上吗？（用方程解）9．把的分子、分母加上同一个数以后，正好可以约成。

这个加上去的数是多少？10．某工厂用一批钢材做零件，每个零件用钢4.5kg，可做160个，改进技术后，每个零件节约用钢1.3kg，改进技术后，这批钢材可做多少个零件？（用方程解）11．如图所示：一个长方体的水槽，被一块玻璃隔板分成左、右两部分。

北师大版小学五年级数学下册全册知识点归纳第一单元《分数加减法》补充知识点：整数加减法运算定律在分数加减法中同样适用，见下图：4、把分数化成小数的方法：通常是利用分数与除法的关系，用分子除以分母来得到。

注意：对于某些分数也可以将它化为分母是10、100、1000之类的分数，然后再直接写成小数形式。

例如：5、常见分数和小数的互化：第二单元《长方体（一）》第一类，中间四连方，两侧各一个，共六种：第二类，中间三连方，两侧各有一、二个，共三种：第四类，两排各三个，只有一种：例如：如图，4个棱长都是10厘米的正方体堆放在墙角处，露在外面的面积是多少？第三单元《分数乘法》约分的最好先约分。

3、打折的含义，例如：九折，是指现价是原价的。

容积单位：升(L) 毫升(ml)补充知识点：冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。

单位换算：（相邻单位之间的进率为1000）（小单位化成大单位要除以进率，大单位化成小单位要乘以进率。

可以概括为：小化大除一下，大化小乘一下）1米3＝1000分米31分米3＝1000厘米31升＝1000毫升 1升＝1分米31毫升＝1厘米3单名数与复名数之间的互化：单名数：由一个数和一个单位名称组成的名数叫做单名数。

分数除以整数的计算方法：分数除以整数（0除外）等于乘这个整数的倒数。

4、整数除以分数等于乘这个分数的倒数。

5、除以一个数（零除外）等于乘这个数的倒数。

的孵化期为x天，则：未知的，所以用鸭的孵化期除以它对应的分率，即：①以学校为观测点，丁丁家的位置是西偏北45°，距离学校1800米。

②以学校为观测点，青青家的位置是东偏北26°，距离学校1500米。

第七单元《用方程解决问题》1、列方程解应用题的步骤：（1）找到题中的等量关系式（2）解设所求量为x（3）根据等量关系式列出相应的方程（4）解答方程，注意计算结果不带单位。

（5）检验做答。

2、在有多个未知数量的应用题中，通常应将1倍数设为x，举例如下：例:爸爸的年龄是儿子年龄的4倍，父子俩年龄之和为40，求父亲和儿子的年龄各是多少岁？解：首先根据题意找出等量关系式：爸爸年龄+儿子年龄=40因为儿子年龄是1倍数，所以：设儿子年龄为x岁，那么爸爸年龄就是4x，代入等量关系式得：爸爸年龄为：4x=4×8=32(岁)答：爸爸的年龄为32岁，儿子的年龄为8岁。

1、一袋大米，第一次吃了103，第二次吃了51，两次一共吃了这袋大米的几分之几？2、小红要折100个纸鹤，第一天折了总数的31，第二天折了总数的52，第二天比第一天多折了总数的几分之几？3、小红、小明和小亮三个小朋友比身高，小红比小亮高152米，小亮比小明高201米，小红与小明相差多少米？4、某商场2014年上半年完成计划销售额的32，下半年完成计划销售额的83，全年的实际销售额超过计划销售额的几分之几？5、一根竹竿插入水塘的泥土中，插入泥中的部分占51，在水中的部分占72，露出水面的部分占几分之几？6、学校买来一匹红布，做红旗用了0.7米，余下的做红领巾，用了32米，这批布一共有多少米？7、有一根木头，第一次截下全部的31，第二次截下全部的52。

（1）两次截下的占木头全长的几分之几？（2）还剩全长的几分之几？8、一个灯笼的框架是长方体（如右图），底面是一个正方形。

制作这样一个框架至少需要多少厘米长的铁条？如果用同样长的铁条做一个正方体框架，这个正方体框架的棱长是多少？（单位：厘米）9、小卖部要把一个长220厘米、宽40厘米、高80厘米的玻璃柜台各边都安上角铁，这个柜台需要多少米角铁？10、用丝带捆扎一个如右图的礼品盒，已知接头处15厘米，捆扎这个礼品盒至少需准备多长的丝带才合适？1、一个茶叶盒高15厘米，长8厘米，宽5厘米。

在茶叶盒的四周围上一圈包装纸，最少需要多少平方厘米的包装纸？2、用玻璃做两个无盖的鱼缸，一个是棱长为4分米的正方体，另一个是长4分米、宽3分米、高5分米的长方体。

哪个鱼缸用的玻璃多？多多少？3、一个游泳池长25m，宽10m，深2m。

要在四壁和底部铺瓷砖，共需要瓷砖多少块？（一块瓷砖的面积为2500cm2)4、将4个棱长是6dm的正方体拼成一个长方体，表面积最小是多少平方分米，最大是多少平方分米？5、计算右面这个立方体图形的表面积。

（单位：cm）6、一个正方体和一个长方体拼成了一个新的长方体，拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米。

北师大版数学五年级下册《包装的学问》说课稿一. 教材分析北师大版数学五年级下册《包装的学问》这一课，主要让学生了解和掌握如何利用数学知识解决实际生活中的包装问题。

通过这一课的学习，使学生能够理解和掌握包装的方法和技巧，提高他们的动手能力和解决问题的能力。

二. 学情分析五年级的学生已经具备了一定的数学基础，他们已经学习了平面图形的知识，对图形的性质和特点有一定的了解。

同时，他们也已经学习了一些简单的数学问题解决方法，具备了一定的解决问题的能力。

但是，对于一些复杂的包装问题，他们可能还不知道如何下手，需要通过本节课的学习，使他们能够理解和掌握包装的方法和技巧。

三. 说教学目标1.让学生理解和掌握包装的方法和技巧，能够运用数学知识解决实际生活中的包装问题。

2.培养学生的动手能力和解决问题的能力。

3.培养学生的创新意识和团队协作能力。

四. 说教学重难点1.教学重点：让学生理解和掌握包装的方法和技巧，能够运用数学知识解决实际生活中的包装问题。

2.教学难点：如何让学生理解和掌握包装的方法和技巧，能够灵活运用数学知识解决实际生活中的包装问题。

五.说教学方法与手段1.采用问题驱动法，让学生在解决问题的过程中理解和掌握包装的方法和技巧。

2.采用案例分析法，让学生通过分析实际案例，理解和掌握包装的方法和技巧。

3.采用小组合作法，让学生在团队协作的过程中，培养他们的创新意识和团队协作能力。

六. 说教学过程1.导入：通过一个实际的包装问题，引发学生的思考，激发他们的学习兴趣。

2.新课导入：介绍包装的方法和技巧，让学生理解和掌握。

3.案例分析：分析一些实际的包装案例，让学生通过分析，进一步理解和掌握包装的方法和技巧。

4.动手实践：让学生分组进行实践活动，运用所学的包装方法和技巧，解决实际问题。

5.总结提升：对所学的包装方法和技巧进行总结，让学生能够灵活运用。

6.课堂小结：对课堂内容进行小结，让学生巩固所学。

七. 说板书设计板书设计主要包括包装的方法和技巧，以及实际案例的分析。

北师大版数学五年级下册《包装的学问》教学设计一. 教材分析北师大版数学五年级下册《包装的学问》一课，主要让学生通过实践活动，探索并掌握“利用最少材料，使包装体积最小”的包装方法。

教材以学生熟悉的包装礼物为情境，引出数学问题，让学生在解决实际问题的过程中，体会数学与生活的联系，培养学生的动手操作能力、空间想象能力和解决实际问题的能力。

二. 学情分析五年级的学生已经具备了一定的观察能力、操作能力和问题解决能力。

他们在学习过程中，能够主动参与活动，发现问题，解决问题。

但是，对于一些空间几何图形的重叠、组合，以及如何用最少的材料进行包装，可能还需要进一步引导和探究。

三. 教学目标1.知识与技能：让学生掌握简单的包装方法，能够运用数学知识解决实际问题。

2.过程与方法：通过观察、操作、猜想、验证等方法，培养学生的空间想象能力和问题解决能力。

3.情感态度与价值观：让学生感受数学与生活的联系，培养学生的动手操作兴趣，提高学生学习数学的积极性。

四. 教学重难点1.教学重点：让学生掌握包装的方法，能够解决实际问题。

2.教学难点：如何让学生理解并掌握“利用最少材料，使包装体积最小”的包装方法。

五. 教学方法1.情境教学法：通过创设情境，让学生在实际问题中感受数学的魅力。

2.动手操作法：让学生在动手操作的过程中，发现问题，解决问题。

3.引导发现法：教师引导学生观察、思考，发现包装的方法和规律。

六. 教学准备1.准备一些包装材料，如纸盒、彩纸等。

2.准备一些教学课件和教学素材。

七. 教学过程1.导入（5分钟）教师通过创设情境，引出包装礼物的问题，激发学生的学习兴趣。

2.呈现（10分钟）教师展示一些包装方法，让学生观察并思考：哪种包装方法用的材料最少？3.操练（15分钟）学生分组进行实践活动，尝试不同的包装方法，并计算所用材料的大小。

4.巩固（10分钟）教师引导学生总结包装的方法和规律，让学生明白如何用最少的材料进行包装。

北师大版小学五年级数学下册期末复习应用题100道(全) 附答案一、北师大小学数学解决问题五年级下册应用题1．某工厂用一批钢材做零件，每个零件用钢4.5kg，可做160个，改进技术后，每个零件节约用钢1.3kg，改进技术后，这批钢材可做多少个零件？（用方程解）2．鱼缸里水深2.8分米，放入一块珊瑚石完全浸没在水中，水面上升到3分米珊瑚石的体积是多少立方分米？3．将一块长10dm，宽8dm的长方形铁皮四个角各剪下一个边长为2dm的正方形（如图），然后焊成一个无盖的长方体水槽。

这个水槽用了多少铁皮？水槽盛水多少升？（不计铁皮的厚度）4．将小正方体按下图靠墙摆放。

小正方体的个数24681012…2a露在外面的面的个数5．有一辆沙土车，每次运沙土1.6m3，如果要在长为43m，宽为15m的长方形地上铺一层厚为4cm的沙土，铺地共需沙土多少立方米？这些沙土至少要运几次？6．有4个棱长是3dm的正方体礼品盒，现在要把它们用包装纸包装起来，有如下两种方案（如下图）。

（1）哪种方案能节省包装纸？（2）至少需要多少平方米的包装纸？7．红铅笔每支1.9元，蓝铅笔每支1.1元，两种铅笔共买了16支，花了28元。

问：红、蓝铅笔各买了几支？8．一根铁丝恰好可以焊接成一个长5厘米，宽3厘米，高4厘米的长方体框架．若这根铁丝也恰好能焊接成一个正方体框架．（1）这个正方体框架的棱长是多少厘米？（2）给这个正方体框架的表面焊接上铁皮，铁皮的面积是多少平方厘米？9．有一块长方体木料（如图，单位：厘米）。

小刚想把它锯成同样大小的两个长方体木块。

怎样锯，表面积增加最多？怎样锯，表面积增加最少？请在下图中画出来。

（1）表面积增加最多的锯法：（2）表面积增加最少的锯法：10．有两袋大米，甲袋大米的质量是乙袋大米的1.2倍。

若从甲袋往乙袋倒4kg大米，则两袋大米一样重。

原来两袋大米各有多少千克？（用方程解答）11．现有空的长方体容器A和水深24厘米的长方体容器B（如图），要将容器B的水倒一部分给A，使两容器水的高度相同，这时水深是几厘米？12．张华买了一批菜油，放在A，B两个桶里，两个桶都未能装满。

北师大版完整版五年级小学数学下册应用题(40题)及答案一、北师大小学数学解决问题五年级下册应用题1．有两袋大米，甲袋大米的质量是乙袋大米的1.2倍。

若从甲袋往乙袋倒4kg大米，则两袋大米一样重。

原来两袋大米各有多少千克？（用方程解答）2．挖一个长10米，宽6米、深2米的蓄水池。

（1）这个蓄水池的占地面积是多少平方米？（2）这个蓄水池已经蓄水1.5米，最多还能蓄水多少立方米？3．少年宫和学校相距800米。

小童和小乐分别从少年宫和学校门口同时向相反方向走去（如下图），7分钟后两人相距1360米。

小童每分钟走37米。

小乐每分钟走多少米？（列方程解）4．某公司订购400根方木，每根方木横截面的面积是25平方分米，长是4米，这些木料一共有多少方？（1方=1立方米）5．将一块长10dm，宽8dm的长方形铁皮四个角各剪下一个边长为2dm的正方形（如图），然后焊成一个无盖的长方体水槽。

这个水槽用了多少铁皮？水槽盛水多少升？（不计铁皮的厚度）6．有4个棱长是3dm的正方体礼品盒，现在要把它们用包装纸包装起来，有如下两种方案（如下图）。

（1）哪种方案能节省包装纸？（2）至少需要多少平方米的包装纸？7．书架有两屠，上层的图书本数是下层的1.5倍，如果从上层拿10本书到下层，那么两层的图书本数一样多。

原来书架的上、下层各有多少本图书?8．一根铁丝恰好可以焊接成一个长5厘米，宽3厘米，高4厘米的长方体框架．若这根铁丝也恰好能焊接成一个正方体框架．（1）这个正方体框架的棱长是多少厘米？（2）给这个正方体框架的表面焊接上铁皮，铁皮的面积是多少平方厘米？9．有一块长32cm，宽16cm的长方形铁皮，通过折、割或焊等方法做出一个高为4cm的无盖长方体盒子，使这个盒子的容积尽可能的大，你会怎样设计？请画出示意图。

（1）我的设计是：长________cm，宽________cm，高4cm。

（2）我画的示意图：（3）请列式计算出它的容积：10．你能把宣传栏上破损的数补上吗？（用方程解）11．光明学校四周的外围墙有些陈旧，现在要将四周的外围墙重新粉刷（不考虑门窗），现在不但要选购涂料，还要请粉刷工人。

北师大版五年级下册《整理与复习（2）》小学数学-有答案-同步练习卷一、基础启航1. 在横线里填上适当的单位。

（1）一块香皂的体积是120________．（2）一瓶饮料约有600________．（3）一台洗衣机的体积约是300________．2. 0.08立方米＝________立方分米560毫升＝________升4060立方厘米＝________立方分米5.3升＝________毫升3. 如图，容器中放了一颗小石子，读数是450mL，取出后读数是300mL．这颗小石子的体积是________．4. 一个长方体的长为6cm，如果将长增加6cm，宽和高不变，那么这个长方体的体积就扩大到原来的________倍。

5. 一个长方体的长a分米，宽b分米，高c分米，若把高增加5分米，则表面积增加________平方分米，体积增加________立方分米。

6. 选一选。

下面能围成正方体的是________，能围成长方体的是________．7. 如图，一些小正方体放在墙角处，有（）个面露在外面。

A.8B.9C.108. 将一个正方体钢坯锻造成长方体，正方体和长方体（）A.体积相等，表面积不相等B.体积和表面积都不相等C.表面积相等，体积不相等D.体积和表面积都相等9. 有5根8厘米和10根10厘米的小棒，用其中12根搭一个长方体，这个长方体棱长总和是（）厘米。

A.5×8+7×10＝110B.4×8+8×10＝112C.5×8+10×10＝140D.(5+8+10)×4＝9210. 把一个长6厘米、宽4厘米、高5厘米的长方体切成两个长方体，表面积最多增加________平方厘米，最少增加________方厘米。

A.60 B.40 C.30 D.2011.（1）求下面图形的棱长总和、表面积和体积。

（2）求下面图形的棱长总和、表面积和体积。