第5章 杆件的应力与强度计算

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁，火车的轮轴，楼房的横梁，阳台的挑梁等。

二、弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线。

变形特点——杆轴线由直线变为一条平面的曲线。

三、梁的概念：主要产生弯曲变形的杆。

四、平面弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线，且都在梁的纵向对称平面内（通过或平行形心主轴且过弯曲中心）。

变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。

五、弯曲的分类：1、按杆的形状分——直杆的弯曲；曲杆的弯曲。

2、按杆的长短分——细长杆的弯曲；短粗杆的弯曲。

3、按杆的横截面有无对称轴分——有对称轴的弯曲；无对称轴的弯曲。

4、按杆的变形分——平面弯曲；斜弯曲；弹性弯曲；塑性弯曲。

5、按杆的横截面上的应力分——纯弯曲；横力弯曲。

六、梁、荷载及支座的简化（一）、简化的原则：便于计算，且符合实际要求。

（二）、梁的简化：以梁的轴线代替梁本身。

（三）、荷载的简化：1、集中力——荷载作用的范围与整个杆的长度相比非常小时。

2、分布力——荷载作用的范围与整个杆的长度相比不很小时。

3、集中力偶（分布力偶）——作用于杆的纵向对称面内的力偶。

（四）、支座的简化：1、固定端——有三个约束反力。

2、固定铰支座——有二个约束反力。

3、可动铰支座——有一个约束反力。

（五）、梁的三种基本形式：1、悬臂梁：2、简支梁：3、外伸梁：（L 称为梁的跨长） （六）、静定梁与超静定梁静定梁：由静力学方程可求出支反力，如上述三种基本形式的静定梁。

超静定梁：由静力学方程不可求出支反力或不能求出全部支反力。

§5—2 弯曲内力与内力图一、内力的确定（截面法）：[举例]已知：如图，F ，a ，l 。

求：距A 端x 处截面上内力。

解：①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力：剪力和弯矩1. 弯矩：M ；构件受弯时，横截面上存在垂直于截面的内力偶矩。

工程力学中的杆件和梁的应力分析工程力学是工程学科的重要分支之一，它研究物体在受力作用下的力学性质。

在工程实践中，杆件和梁是常见的结构构件，其应力分析是工程设计和计算的基础。

本文将从杆件和梁的应力分析角度探讨工程力学中的相关知识。

一、杆件的应力分析杆件是一种细长的结构构件，承受轴向力的作用。

在杆件的静力学中，应力是一个重要参数，用于描述杆件内部受力的强度和稳定性。

杆件的应力可以分为正应力和切应力。

1. 正应力正应力是指垂直于杆件截面的作用力在该截面上的单位面积，通常用σ表示。

正应力的计算可以使用公式：σ = F / A其中，F为作用力的大小，A为截面积。

正应力可以分为拉应力和压应力两种情况。

当作用力沿着杆件的轴向，方向与截面的法线方向一致时，称为拉应力。

拉应力是正值，表示杆件受拉的状态。

当作用力沿着杆件的轴向，方向与截面的法线方向相反时，称为压应力。

压应力是负值，表示杆件受压的状态。

2. 切应力切应力是指杆件截面上作用力的切向力与该截面上的单位面积之比，通常用τ表示。

切应力的计算可以使用公式：τ = F / A其中，F为作用力的大小，A为截面积。

切应力主要存在于杆件的连接部分，例如螺纹连接、焊接连接等。

切应力会引起杆件的剪切变形和破坏，需要在设计过程中加以考虑。

二、梁的应力分析梁是一种用于承受弯曲力的结构构件，具有横截面的特点。

在梁的应力分析中，主要考虑的是弯矩和截面弯曲应力。

1. 弯矩弯矩是指作用在梁上的力对其产生的弯曲效应。

在工程实践中，梁通常是直线形状，因此弯矩在横截面上呈现出分布的特点。

弯矩可以通过力学平衡和弹性力学原理进行计算。

弯矩的大小与力的大小和作用点的位置有关，计算公式为：M = F * d其中，M为弯矩，F为作用力的大小，d为作用点到梁的某一端的距离。

2. 截面弯曲应力截面弯曲应力是指由于弯曲效应，在梁的横截面上产生的应力。

截面弯曲应力的大小与弯矩和横截面的几何形状有关，计算可以使用弯曲应力公式进行。

杆件屈服应力计算公式在工程力学中，杆件屈服应力是一个非常重要的参数，它可以帮助工程师确定杆件在受力时是否会发生屈服现象。

屈服现象是指在杆件受到一定的外力作用时，杆件内部会出现塑性变形，导致杆件失去原有的弹性特性。

因此，计算杆件屈服应力是非常重要的，可以帮助工程师选择合适的材料和设计合理的结构。

杆件屈服应力的计算公式可以通过材料的力学性能参数来确定，一般来说，常见的材料力学性能参数包括杨氏模量、屈服强度和断裂强度等。

通过这些参数，可以得到杆件屈服应力的计算公式如下：σ_yield = F_y / A。

其中，σ_yield表示杆件的屈服应力，F_y表示材料的屈服强度，A表示杆件的横截面积。

从这个公式可以看出，杆件的屈服应力与材料的屈服强度和杆件的横截面积有关。

材料的屈服强度越大，杆件的屈服应力也会越大；而杆件的横截面积越大，杆件的屈服应力也会越大。

在实际工程中，工程师需要根据具体的材料和结构设计要求来确定杆件的屈服应力。

一般来说，材料的屈服强度可以通过材料的力学性能表来查找，而杆件的横截面积可以通过几何参数来计算。

在计算杆件的屈服应力时，工程师还需要考虑杆件的受力情况，例如受拉、受压或受弯等情况，这些都会对杆件的屈服应力产生影响。

除了杆件的屈服应力，工程师在设计结构时还需要考虑杆件的安全系数。

安全系数是指杆件的实际强度与设计强度之间的比值，通过安全系数可以评估杆件在受力时的安全性。

一般来说，工程师会根据设计要求和材料的力学性能来确定安全系数的大小，以确保结构在受力时不会发生屈服现象。

总的来说，杆件屈服应力是一个非常重要的参数，在工程设计中起着至关重要的作用。

通过合理计算杆件的屈服应力，可以帮助工程师选择合适的材料和设计合理的结构，从而确保结构在受力时具有足够的强度和稳定性。

同时，工程师还需要考虑安全系数等因素，以确保结构在受力时不会出现屈服现象，从而保障工程的安全性和可靠性。

eBook工程力学（静力学与材料力学）习题详细解答（教师用书）(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5－1试用截面法计算图示杆件各段的轴力，并画轴力图。

解：(a)题(b)题(c)题(d)题习题5－1图F NxF N(kN)x-3F Nx A5－2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。

直杆各部分的直径均为d ＝36 mm ，受力如图所示。

若不考虑杆的自重，试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解：()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5－3 长度l ＝1.2 m 、横截面面积为1.10×l0－3 m 2的铝制圆筒放置在固定的刚性块上；-10F N x习题5－2图刚性板固定刚性板A E mkN习题5－4解图直径d ＝15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上；铝制圆筒的轴线与钢杆的轴线重合。

若在钢杆的C 端施加轴向拉力F P ，且已知钢和铝的弹性模量分别为E s ＝200GPa ，E a ＝70GPa ；轴向载荷F P ＝60kN ，试求钢杆C 端向下移动的距离。

解： a a P A E l F u u ABB A −=−（其中u A = 0）∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5－4 螺旋压紧装置如图所示。

《工程力学》第6次作业解答（杆件的应力与强度计算）2010-2011学年第2学期一、填空题1．杆件轴向拉压可以作出平面假设：变形前为平面的横截面，变形后仍保持为平面，由此可知，横截面上的内力是均匀分布的。

2．低碳钢拉伸可以分成：弹性阶段、屈服阶段、强化阶段、缩颈阶段。

3．如果安全系数取得过大，许用应力就偏小；需用的材料就偏多而造成浪费；反之，安全系数取得太小，构件的强度就可能不够。

4．延伸率和面积收缩率是衡量材料塑性性能的两个重要指标。

工程上通常把延伸率δ≥5%的材料称为塑性材料，延伸率δ＜5%的材料称为脆性材料。

5．在国际单位制中，应力的单位是帕，1帕=1牛/米2，工程上常以Pa 、MPa 、 GPa 为应力的单位。

6．轴向拉伸和压缩强度条件的表达式是：][max σσ≤=A F N ，用该强度条件可解决的三类强度问题是：校核强度、设计截面、确定许用载荷。

7．二根不同材料的等直杆，承受相同轴力，且它们的截面面积及长度都相等，则：（1）二根杆横截面上的应力相同；（2）二根杆的强度不同；（3）二根杆的绝对变形不相同。

（填相同或不相同）8．在承受剪切的构件中，相对错动发生的截面，称为剪切面；构件在受剪切时，伴随着发生挤压作用。

9．构件在剪切变形时的受力特点是作用在构件上的外力垂直于轴线，两侧外力大小相等，方向相反，作用线平行但相距很近；变形特点是两个反向外力之间的截面发生相对错动。

剪切变形常发生在联接零件上，如螺栓、键、销钉等。

10．剪切面在两相邻外力作用线之间，与外力作用线平行。

11．圆轴扭转时，横截面上的切应力与半径垂直，在同一半径的圆周上各点的切应力大小相等，同一半径上各点的切应力按线性规律分布，轴线上的切应力为零，外圆周上各点切应力最大。

12．圆轴扭转时的平面假设指出：扭转变形后，横截面本身的形状、大小不变，相邻截面间的距离保持不变，各截面在变形前后都保持为平面，只是绕轴线转过一个角度，因此推出：横截面上只存在切应力，而不存在正应力。

杆件的强度计算公式资料讲解杆件的强度、刚度和稳定性计算1.构件的承载能⼒，指的是什么？答：构件满⾜强度、刚度和稳定性要求的能⼒称为构件的承载能⼒。

(1)⾜够的强度。

即要求构件应具有⾜够的抵抗破坏的能⼒，在荷载作⽤下不致于发⽣破坏。

(2)⾜够的刚度。

即要求构件应具有⾜够的抵抗变形的能⼒，在荷载作⽤下不致于发⽣过⼤的变形⽽影响使⽤。

(3)⾜够的稳定性。

即要求构件应具有保持原有平衡状态的能⼒，在荷载作⽤下不致于突然丧失稳定。

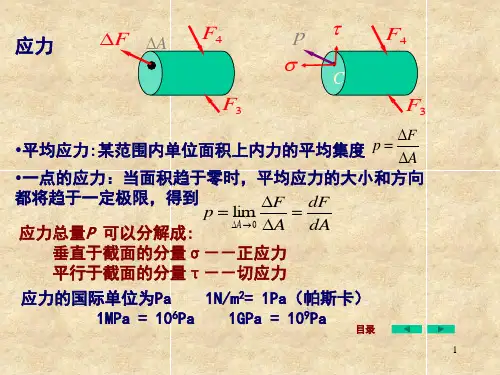
2.什么是应⼒、正应⼒、切应⼒？应⼒的单位如何表⽰？答：内⼒在⼀点处的集度称为应⼒。

垂直于截⾯的应⼒分量称为正应⼒或法向应⼒，⽤σ表⽰；相切于截⾯的应⼒分量称切应⼒或切向应⼒，⽤τ表⽰。

应⼒的单位为Pa。

1 Pa=1 N／m2⼯程实际中应⼒数值较⼤，常⽤MPa或GPa作单位1 MPa=106Pa1 GPa=109Pa3.应⼒和内⼒的关系是什么？答：内⼒在⼀点处的集度称为应⼒。

4.应变和变形有什么不同？答：单位长度上的变形称为应变。

单位纵向长度上的变形称纵向线应变，简称线应变，以ε表⽰。

单位横向长度上的变形称横向线应变，以ε/表⽰横向应变。

5.什么是线应变？什么是横向应变？什么是泊松⽐？答：（1）线应变单位长度上的变形称纵向线应变，简称线应变，以ε表⽰。

对于轴⼒为常量的等截⾯直杆，其纵向变形在杆内分布均匀，故线应变为l l?=ε（4-2）拉伸时ε为正，压缩时ε为负。

线应变是⽆量纲（⽆单位）的量。

（2）横向应变拉(压)杆产⽣纵向变形时，横向也产⽣变形。

设杆件变形前的横向尺⼨为a，变形后为a1，则横向变形为aaa-=1横向应变ε/为a a=/ε（4-3）杆件伸长时，横向减⼩，ε/为负值；杆件压缩时，横向增⼤，ε/为正值。

因此，拉(压)杆的线应变ε与横向应变ε/的符号总是相反的。

（3）横向变形系数或泊松⽐试验证明，当杆件应⼒不超过某⼀限度时，横向应变ε/与线应变ε的绝对值之⽐为⼀常数。

此⽐值称为横向变形系数或泊松⽐，⽤µ表⽰。

杆件的强度计算公式1.应力：应力是杆件内部单位面积上的力，通常以帕斯卡（Pa）为单位。

应力被定义为负载除以横截面积。

在强度计算中，应力是一个重要的参数，用于评估杆件是否能够承受给定的负载。

2.截面形状：截面形状指的是杆件横截面的形状，如圆形、矩形、梯形等。

截面形状对杆件的强度计算有很大影响，因为不同的形状在承载能力方面具有不同的特点。

3.材料性质：杆件的材料性质包括弹性模量、屈服强度、抗拉强度等。

这些参数用于计算杆件在受力情况下的应力和应变，并评估其强度。

根据杆件的受力类型和计算方法的不同，强度计算公式可以有很多种形式。

以下是几个常见的强度计算公式示例：1.杆件的拉伸强度计算公式：拉伸强度=屈服强度/安全系数这个公式适用于纯拉伸情况下的杆件强度计算。

通常，设计中会采用一个安全系数，以确保杆件在实际应用中不会超过其屈服强度。

2.杆件的压缩强度计算公式：压缩强度=屈服强度/安全系数这个公式适用于纯压缩情况下的杆件强度计算。

与拉伸情况类似，设计中也会采用一个安全系数。

3.杆件的弯曲强度计算公式：弯曲强度=弯矩/抗弯矩弯曲强度计算涉及到杆件的几何形状和截面惯性矩等参数，以及杆件的材料性质。

通过计算弯矩和抗弯矩的比值，可以评估杆件在受弯应力作用下的强度。

此外，还有一些特殊情况下的杆件强度计算公式，如扭转、剪切、冲击等。

这些公式通常相对复杂，需要更详细的材料性质和截面形状参数。

需要注意的是，强度计算公式只是一种初步评估杆件承载能力的方法，它没有考虑杆件的缺陷、损伤和非均匀加载等因素。

因此，在实际工程中，还需要进行更为详细的强度分析和安全性评估，以确保杆件的可靠性和安全性。