双对数函数模型
- 格式:doc
- 大小:82.50 KB
- 文档页数:3

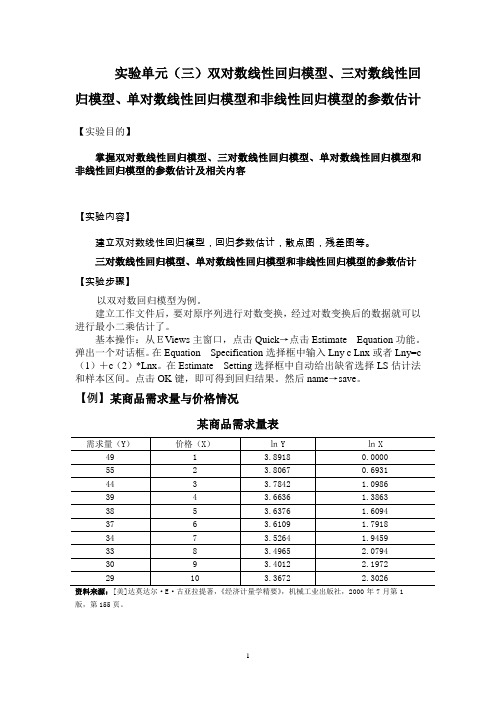
实验单元(三)双对数线性回归模型、三对数线性回归模型、单对数线性回归模型和非线性回归模型的参数估计【实验目的】掌握双对数线性回归模型、三对数线性回归模型、单对数线性回归模型和非线性回归模型的参数估计及相关内容【实验内容】建立双对数线性回归模型,回归参数估计,散点图,残差图等。
三对数线性回归模型、单对数线性回归模型和非线性回归模型的参数估计【实验步骤】以双对数回归模型为例。
建立工作文件后,要对原序列进行对数变换,经过对数变换后的数据就可以进行最小二乘估计了。
基本操作:从EViews主窗口,点击Quick→点击Estimate Equation功能。
弹出一个对话框。
在Equation Specification选择框中输入Lny c Lnx或者Lny=c (1)+c(2)*Lnx。
在Estimate Setting选择框中自动给出缺省选择LS估计法和样本区间。
点击OK键,即可得到回归结果。
然后name→save。
【例】某商品需求量与价格情况某商品需求量表资料来源:[美]达莫达尔·E·古亚拉提著,《经济计量学精要》,机械工业出版社,2000年7月第1版,第155页。
要求:一、 理论阐述由经济理论知,商品的需求量受商品价格的影响。
一般而言,当价格上升时,商品的需求量会随之下降,而价格下降时,商品的需求量会上升。
它们之间具有反向的变动趋势。
商品的需求量除受价格的影响之外,还要受到其他一些变量的影响及随机因素的影响,在这里,把其他变量及随机因素的影响均归并到随机变量u 中,建立某商品的需求量Y 和价格X 之间的双变量总体线性回归模型:Y i =β0+β1X i +u i ,其中,Y i 表示某商品的需求量,X i 表示某商品的价格,β0、β1为待定系数,u i 表示随机误差项。
二、 做X 、Y 散点图确定了模型后,需要在直观上初步探明变量之间的相互关系,为此,以此商品的价格为横轴,以商品的需求量为纵轴,描出样本变量观测值的散点分布图。

基于R语言的互补双对数模型分析作者:戴建国杨剑红来源:《宁波职业技术学院学报》2017年第04期摘要:针对分类数据模型的误差不满足正态分布,Logistic分布等常用分布,而是满足极值分布这类特殊情况时,采用互补双对数模型进行分析。
以R语言作为分析工具,并将其与几种常用模型进行对比分析,结果表明互补双对数模型优于其他模型。
关键词:互补双对数模型; R语言;有序分类中图分类号: O 212.1 文献标志码: A 文章编号: 1671-2153(2017)04-0087-031 问题提出大数据时代,数据挖掘与数据分析过程中遇到的数据类型主要有连续型,离散型,以及混合型,其涉及的方法众多,如机器学习,深度学习等。
当然,对于离散型数据,回归模型也是比较流行的统计分析方法之一,而且在多数情况下,因变量有可能是有序二分类或多分类的离散型变量,在医疗卫生统计或社会统计尤为常见,如对某事的评价可能分为不好、好、非常好这样三个等级。
对于这类数据常用的模型有Logistic回归模型(包括累积Logistic,邻近Logistic等模型),Probit回归模型,但它们分别是假设模型误差分布是Logistic分布和正态分布的,而有些情况误差并不满足这样的假设,其误差分布是非对称的极值分布或称Gumbel 分布[1]。
如某年某河面最高水位这样一个极值,这时需要寻求一个更为有效的模型,此时采用互补双对数线性模型与其他几种模型进行对比分析。
并且近年来R语言已成为当下最流行做数据分析和挖掘的工具之一,它不仅有丰富的函数包,而且能与Hadoop,Python等软件结合,使得成为重要的数据分析工具。
下面基于R语言用互补双对数模型对一组实际数据进行对比分析。
2 互补双对数线性模型[1]该模型的一般形式为log{-log[1-P(Y≤j)]}=αj+β'X,(1)从而可得求概率的表达式为式中:αj为解释变量不能解释的部分;β'为参数构成的向量。

计量经济学习题集1双对数模型LNY=LN β0+β1LNX+µ中,参数β1的含义是AY 关于X 的增长率 BY 关于X 的发展速度 CY 关于X 的弹性D Y 关于X 的边际变化 2设K 为回归模型中的参数个数,n 为样本容量。
则对多元线性回归⽅程进⾏显著性检验时,所⽤的F 统计量可表⽰为() A )1_/()_/(K RSS k n ESS B. 3回归分析众使⽤的距离是点到直线的垂直坐标距离。
最⼩⼆乘准则是指A 使y4回归模型中具有异⽅差性时,仍⽤OLS 估计模型,则以下说法正确的是A 参数估计值是⽆偏⾮有效的B 参数估计量仍具有最⼩⽅差性C 常⽤F 检验失效D 参数估计量是有偏的判断题:1\简单线性回归模型与多元线性回归模型的基本假定是相同的2在模型中引⼊解释变量的多个滞后项容易产⽣多重共线性3DW 检验众的d 值在0到4之间,数值越⼩说明模型随机误差项的⾃相关度越⼩,反之则越⼤。
4\在计量经济模型中,随机扰动项与残差项⽆区别5在经济计量分析中,模型参数⼀旦被估计出来,就可将估计模型直接运⽤于实际的计量经济分析。
经济计量模型是指()A 投⼊产出模型B 数学规划模型C 包含随机⽅程的经济数学模型D 模糊数学模型10、在回归模型中,正确地表达了随机扰动项序列相关的是( A )A. COV (µ i ,µ j ) ≠ 0, i ≠ jB. COV (µ i , µ j ) = 0, i ≠ jC. ( , ) 0, i j COV X X = i ≠ jD. COV ( X i ,µ j ) ≠ 0, i ≠ j9、对于有限分布滞后模型t t t t k t k t Y = + X + X + X + + X + u ? ? ? αβ 0 β 1 1 β 2 2 β在⼀定条件下,参数iβ可近似⽤⼀个关于i 的阿尔蒙多项式表⽰(i = 0,1,2,,m ),其中多项式的阶数m 必须满⾜( A )A .m < kB .m = kC .m > kD .m ≥ k4、在给定的显著性⽔平之下,若DW 统计量的下和上临界值分别为d L 和d U ,则当 L U dA.存在⼀阶正⾃相关B.存在⼀阶负相关C.不存在序列相关D.存在序列相关与否不能断定5、在线性回归模型中,若解释变量X 1i 和X 2i 的观测值成⽐例,即有X 1i = kX 2i ,其中 k 为⾮零常数,则表明模型中存在( B )A. 异⽅差B. 多重共线性C. 序列⾃相关D. 设定误差11、在DW 检验中,存在负⾃相关的判定区域是( A )A. 4- d l ﹤ d ﹤4B. 0﹤ d ﹤d lC. d u ﹤ d ﹤4- d uD. d l ﹤ d ﹤d u ,4- d u ﹤ d ﹤4- d l14、下列说法不正确的是( C )A.⾃相关是⼀种随机误差现象B.⾃相关产⽣的原因有经济变量的惯性作⽤C.检验⾃相关的⽅法有F 检验法D.修正⾃相关的⽅法有⼴义差分法15、利⽤德宾h 检验⾃回归模型扰动项的⾃相关性时,下列命题正确的是(B )A. 德宾h 检验只适⽤⼀阶⾃回归模型B. 德宾h 检验适⽤任意阶的⾃回归模型C. 德宾h 统计量渐进服从t 分布D. 德宾h 检验可以⽤于⼩样本问题16、对联⽴⽅程组模型估计的⽅法主要有两类,即( A )A. 单⼀⽅程估计法和系统估计法B. 间接最⼩⼆乘法和系统估计法C. 单⼀⽅程估计法和⼆阶段最⼩⼆乘法D. ⼯具变量法和间接最⼩⼆乘法18、调整后的判定系数R2 与判定系数R2 之间的关系叙述不正确的有( A )A. R2 与R2均⾮负C.判断多元回归模型拟合优度时,使⽤R2D.模型中包含的解释变量个数越多,R 2 与R2 就相差越⼤E.只要模型中包括截距项在内的参数的个数⼤于1,则R2 < R219、加权最⼩⼆乘法是( C )的⼀个特例A.⼴义差分法B.普通最⼩⼆乘法C.⼴义最⼩⼆乘法D.两阶段最⼩⼆乘法第九套⼀、单项选择题1、在满⾜经典假定条件的回归分析中,下列有关解释变量和被解释变量的说法正确的有( C )A.被解释变量和解释变量均为⾮随机变量B. 被解释变量和解释变量均为随机变量C.被解释变量为随机变量,解释变量为⾮随机变量D. 被解释变量为⾮随机变量,解释变量为随机变量2、根据样本资料估计得出⼈均消费⽀出Y对⼈均收⼊X的回归模型为ln i Y=2.00+0.75lnXi,这表明⼈均收⼊每增加1%,⼈均消费⽀出将增加( B )∧A. 0.2%B. 0.75%C. 2%D. 7.5%3、回归分析中使⽤的距离是点到直线的垂直坐标距离。

Log-log双对数标准曲线绘制教程1. 实验做双孔,实验结果如下表所示。
2)各标准点吸光值取均值。
在表中OD均一列。
3)如说明书上可能会要求直接使用OD均值作图,也可能要求减去空白吸光值或零标准的非特异吸光值。
4)在log-log坐标纸上绘图。
5)坐标纸上横轴从左至右第一个1-9表示为第一个10进位,第二个1-9表示为第二个10进位。
第三个1-9表示为第三个10进位。
也就是说,如果第一个1代表0.1ng/ml,则第二个1代表1ng/ml,第三个1代表10ng/ml。
因为本次实验标准曲线范围是从2IU/ml到100IU/ml,则可以用第一个1代表1IU/ml,第二个1代表10IU/ml,第三个1代表100IU/ml。
6)坐标纸上纵轴也是同样的。
因为吸光值一般是从0.01~2.5之间。
则可用第一个1代表0.01,第2个1代表0.1,第三个1代表1。
7)曲线第一个数值点是(2,0.123)。
则在横轴左起点的2处向上至第二个1到2之间,这里的1是0.1,2是0.2。
其间分为10个小格,每个小格是0.01。
因此从第二个1向上2.3个小格。
8)曲线第二个数值点是(7,0.3505)。
则在横轴左起点的7处向上至第二个3到4之间,这里的3是0.3,4是0.4。
其间分为5个小格,每个小格是0.02。
因此从第二个3向上约2个半小格。
9)曲线第三个数值点是(40,1.3385)。
则在横轴从左至右的第2个4处向上至第三个1到2之间,这里的1是1.0,2是2.0。
其间分为10个小格,每个小格是0.1。
因此从第三个1向上约3.4个小格。
10)曲线第四个数值点是(100,2.467)。
则在横轴从左向右的第3个1处。
这个1是指100IU/ml。
向上至第三个2到3之间,这里的2是2.0,3是3.0。
其间分为10个小格,每个小格是0.1。
因此从第三个2向上约5个小格。
12)画一条通过各点的直线。
要求尽可能多的点在线上,同时剩余的点均匀分布在直线的两边。

WORD 格式
专业资料整理
关于双对数模型和半对数模型的斜率系数的经济含义的解释
1.双对数模型 lnY
ln 12lnX
u
d(lnY)
d(lnY)
dY
1 dY dY
d(lnY)
dX
*
dX
Y * X dY
Y
dY
dX e 则2=
d(lnX) 1 1 Y *
dX d(lnX)
dX
dX X
X
X
dQ 可以发现这个就
是
Y 对X 的弹性,请参考微观经济学中需求的价格弹性定义公式 ed= Q 。
dP
P 2.半对数 2
Xu
Y 2
lnXu
lnY
1
1
d(lnY) d(lnY) dY 1 dY (dY
)
Y
2 dX dY * Y * dX dX
dX 这个表示X 的单位绝对变化量导致 Y 的相对变化量(变化率)。
2 dY dY * dX dY * 1 dY * 1 dY d(lnX)
dX
d(lnX)
dX d(lnX) dX 1
dX
dX
( )
X X
这个就是X 的单位相对变化量导致 Y 的绝对量的变化量。
注:在微积分中符号 d 表示无穷小变化,除以原来的绝对量就是相对变化量或者说是变化率。
而还是不够准确,它是具体的数值,所以就会说近似了。
要学会用微积分的观点看就简单了,而且
我们开始求导数是可以把左边的被解释变量本身或者自然对数作为纵轴,把右边的解释变量的本身或者自然对数作为横轴,那么导数的几何意义就是曲线的斜率了。
2、双对数函数模型(幂函数模型) 模型形式: u x b b y ++=ln ln 10(该模型是将u b e Ax y 1=两边取对数,其中A b ln 0=)。
我们将以上模型称为双对数(double-log)模型或称为对数--线性(log-liner)模型。
作如下变换:x x y y ln ,ln **==将其代入原模型,则原模型转化为线性回归模型:u x b b y ++=*10*变换后的模型不仅参数是线性的,而且通过变换后的变量间也是线性的。
模型特点:双对数模型的斜率1b 度量了y 对x 的弹性:xdx ydy x d y d b //)(ln )(ln 1==模型适用对象:对观测值取对数,将取对数后的观测值(lnx,lny )描成散点图,如果近似为一条直线,则适合于双对数模型来描述x 与y 的变量关系。
将两个变量的对数线性回归模型推广到多元,例如,在生产函数的分析中,经常采用以下的柯布——道格拉斯生产函数形式:u e K AL Q βα=式中:Q --产出量,K --资本投入量,L --劳动投入量,A ,βα,为未知参数。
对上式两边取对数得到如下模型:u K L A Q +++=ln ln ln ln βα再令:L L Q Q ln ,ln **==,K K A ln ln,**==,得到线性模型:u K L A Q +β+α+=****模型中的α、β分别为劳动、资本的产出弹性:L dL Q dQ L d Q d //)(ln )(ln ==α;KdK QdQ K d Q d //)(ln )(ln ==β例根据下表给出的1978—2002年间总产出(用国内生产总值GDP度量,单位:亿元),劳动投入(用从业人员度量,单位为万人),以及资本投入(用固定资本度量,单位:亿元)。
运用OLS法建立我国的柯布一道格斯生产函数。
表2利用Eviews软件解题如下:首先建立工作文件,其次输入样本数据Q、L、K,再次,在Eviews软件的命令窗口,依次键入:GENR LNGDP=LOG(GDP)GENR LNL=LOG(L)GENR LNK=LOG(K)LS LNGDP C LNL LNK输出结果如下:由此建立的我国柯布一道格斯生产函数为:K L GDP ln 74759.0ln 71365.0403778.4ln ++-=)ˆ(i b s =(3.539284) (0.363194) (O.053038) t=(-1.244257) (1.964930) (14.09537)994632.02=R 994095.02=R F=1852.869 S.E=0.083623DW=0.669052对回归方程解释如下:偏斜率系数0.71365表示产出对劳动投入的弹性,也就是说,0.71365表示在资本投入保持不变的条件下,劳动投入每增加一个百分点,平均产出将增加0.71%。
对数函数十大模型1. 基本对数函数(logarithmic function)基本对数函数是指形式为f(x) = log<sub>b</sub>(x)的函数,其中b是一个大于0且不等于1的常数。
这个模型在数学和科学领域中具有广泛的应用,例如在对数运算、指数运算和函数的图像研究中。
基本对数函数有以下特性:- 对于x > 0,f(x)是一个实数。
- 对于x = 1,f(x) = 0。
- 对于0 < x < 1,f(x)为负数。
- 对于x > 1,f(x)为正数。
- 函数图像呈现出一个增长不断放缓的曲线。
2. 自然对数函数(natural logarithm function)自然对数函数是基本对数函数的一种特殊形式,记作ln(x)。
其中,底数b取常数e(欧拉数),即ln(x) = log<sub>e</sub>(x)。
自然对数函数与基本对数函数的区别在于其底数取常数e,具有以下特性:- 近似值e约等于2.。
- 对于x > 0,ln(x)为正数。
- 对于x = 1,ln(x) = 0。
- 对于0 < x < 1,ln(x)为负数。
- 函数图像呈现出一个增长不断放缓的曲线。
3. 双曲线正弦函数(hyperbolic sine function)双曲线正弦函数是指形式为f(x) = sinh(x)的函数,在数学和物理领域中具有广泛的应用。
双曲线正弦函数具有以下特性:- sinh(x) = (e<sup>x</sup> - e<sup>-x</sup>)/2。
- 函数图像呈现出一个对称的凸形曲线。
4. 双曲线余弦函数(hyperbolic cosine function)双曲线余弦函数是指形式为f(x) = cosh(x)的函数,与双曲线正弦函数相似,具有以下特性:- cosh(x) = (e<sup>x</sup> + e<sup>-x</sup>)/2。
2、双对数函数模型(幂函数模型) 模型形式: u x b b y ++=ln ln 10
(该模型是将u b e Ax y 1=两边取对数,其中A b ln 0=)。
我们将以上模型称为双对数(double-log)模型或称为对数--线性(log-liner)模型。
作如下变换:
x x y y ln ,ln **==
将其代入原模型,则原模型转化为线性回归模型:
u x b b y ++=*10*
变换后的模型不仅参数是线性的,而且通过变换后的变量间也是线性的。
模型特点:双对数模型的斜率1b 度量了y 对x 的弹性:
x
dx y
dy x d y d b //)(ln )(ln 1==
模型适用对象:对观测值取对数,将取对数后的观测值(lnx,lny )描成散点图,如果近似为一条直线,则适合于双对数模型来描述x 与y 的变量关系。
将两个变量的对数线性回归模型推广到多元,例如,在生产函数的分析中,经常采用以下的柯布——道格拉斯生产函数形式:
u e K AL Q βα=
式中:Q --产出量,K --资本投入量,L --劳动投入量,A ,βα,为未知参数。
对上式两边取对数得到如下模型:
u K L A Q +++=ln ln ln ln βα
再令:L L Q Q ln ,ln **==,K K A ln ln,**==,得到线性模型:
u K L A Q +β+α+=****
模型中的α、β分别为劳动、资本的产出弹性:
L dL Q dQ L d Q d //)(ln )(ln ==
α;K
dK Q
dQ K d Q d //)(ln )(ln ==β
例根据下表给出的1978—2002年间总产出(用国内生产总值GDP度量,单位:亿元),劳动投入(用从业人员度量,单位为万人),以及资本投入(用固定资本度量,单位:亿元)。
运用OLS法建立我国的柯布一道格斯生产函数。
表2
利用Eviews软件解题如下:首先建立工作文件,其次输入样本数据Q、L、K,再次,在Eviews软件的命令窗口,依次键入:
GENR LNGDP=LOG(GDP)
GENR LNL=LOG(L)
GENR LNK=LOG(K)
LS LNGDP C LNL LNK
输出结果如下:
由此建立的我国柯布一道格斯生产函数为:
K L GDP ln 74759.0ln 71365.0403778.4ln ++-=
)ˆ(i b s =(3.539284) (0.363194) (O.053038) t=(-1.244257) (1.964930) (14.09537)
994632.02=R 994095.02=R F=1852.869 S.E=0.083623
DW=0.669052
对回归方程解释如下:
偏斜率系数0.71365表示产出对劳动投入的弹性,也就是说,0.71365表示在资本投入保持不变的条件下,劳动投入每增加一个百分点,平均产出将增加0.71%。
类似地,在劳动投入保持不变的条件下,资本投入每增加一个百分点,产出将平均增加0.75%。