相平面分析

微分方程是数学中的重要概念，它描述了变化率与状态之间的关系。

在解微分方程时，相平面分析是一种常用的方法。

相平面分析通过将微分方程转化为相平面上的轨迹，来揭示方程的性质与解的行为。

相平面是指由自变量和因变量组成的平面。

在微分方程中，自变量通常表示时间，因变量表示系统的状态。

将微分方程转化为相平面上的轨迹，实际上是将微分方程转化为一条或多条曲线，这些曲线反映了系统状态随时间变化的规律。

相平面分析的一般步骤如下：首先，将微分方程化为一阶形式。

多数微分方程可以化为 dx/dt = f(x, t) 的形式，其中 x 表示系统的状态，t 表示时间。

然后，找到微分方程的关键点。

关键点是使得 dx/dt = 0 的点，也即是在相平面上函数曲线的极值点或交点。

接下来，画出函数曲线的大致形状。

可以通过选取几个具体的 x 值，代入微分方程中计算对应的 dx/dt 值，从而得到曲线在相平面上的走向。

在画曲线时，需要特别关注关键点的性质。

分析关键点的稳定性是相平面分析的核心。

对于关键点，可以计算 dx/dt 的导数在该点处的值，从而得到关键点的稳定性。

当 dx/dt 导数为正时，关键点是不稳定的，曲线从该点离开；当 dx/dt 导数为负时，关键点是稳定的，曲线会向该点聚拢；当 dx/dt 导数为零时，需要进一步进行分析。

通过分析关键点的稳定性，可以得到微分方程在相平面上的稳定区域和不稳定区域。

在稳定区域内，系统的状态会从任意初始条件下趋向于关键点，而在不稳定区域内，系统的状态则会趋向于无穷远。

相平面分析不仅可以揭示微分方程的稳定性，还可以帮助我们理解方程的解的行为。

通过观察曲线在相平面上的轨迹，我们可以得到方程解的大致形态和变化规律。

例如，考虑一个简单的线性微分方程 dx/dt = -kx，其中 k 是常数。

这个方程描述了一个稳定的减衰过程。

通过相平面分析，我们可以得到关键点 x = 0，该点稳定且吸引系统状态趋于零。

曲线在相平面上的轨迹是一组从正数推向零的曲线。

第1篇一、实验目的1. 理解相平面的概念及其在控制系统中的应用；2. 掌握相平面分析方法，通过分析相轨迹图，了解系统的动态特性；3. 分析饱和非线性环节对控制系统性能的影响。

二、实验原理相平面分析是一种研究非线性系统动态特性的方法。

它通过将系统的状态变量绘制在二维平面上，形成相轨迹图，从而直观地观察系统的运动规律。

在相平面上，系统的状态变量可以是系统的位置和速度，也可以是系统的其他两个相互独立的变量。

本实验主要研究带有饱和非线性环节的控制系统。

饱和非线性环节具有上限和下限，当输入信号超出这个范围时，系统的输出将不再改变。

在相平面上，饱和非线性环节表现为相轨迹的折线。

三、实验设备1. PC机一台；2. MATLAB软件；3. Simulink模块库。

四、实验步骤1. 建立控制系统模型根据实验要求，建立带有饱和非线性环节的控制系统模型。

首先，建立系统的传递函数，然后添加饱和非线性环节模块。

2. 设置仿真参数设置仿真参数，包括仿真时间、采样时间等。

3. 运行仿真运行仿真，观察系统输入饱和非线性环节前后的相轨迹图。

4. 分析相轨迹图对比有无非线性环节的相轨迹图，分析饱和非线性环节对系统性能的影响。

5. 求解超调量在输入单位阶跃信号的情况下，计算系统的超调量。

五、实验结果与分析1. 相轨迹图分析在饱和非线性环节的影响下，系统的相轨迹图发生了明显的变化。

当输入信号超出饱和非线性环节的上下限时，相轨迹图出现折线。

这表明饱和非线性环节限制了系统的运动范围，影响了系统的动态性能。

2. 系统性能分析通过对比有无非线性环节的相轨迹图，可以发现饱和非线性环节对系统的超调量和上升时间有一定影响。

当饱和非线性环节存在时，系统的超调量增大，上升时间变长。

这是因为饱和非线性环节限制了系统的运动范围，导致系统在达到稳定状态之前需要更多的能量。

3. 超调量计算在输入单位阶跃信号的情况下，系统的超调量为：超调量 = (终值 - 原始值) / 原始值其中，终值为系统稳定后的输出值，原始值为输入信号的幅值。

7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。

但是，我们在介绍非线性系统的分析方法之前，先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。

因为许多非线性元件特性一般都可分段用线性方程来表示，所以非线性控制系统也可以用分段线性系统来近似。

一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在e e -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e e T +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。

但是，我们在介绍非线性系统的分析方法之前，先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。

因为许多非线性元件特性一般都可分段用线性方程来表示，所以非线性控制系统也可以用分段线性系统来近似。

一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在e e -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e e T +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

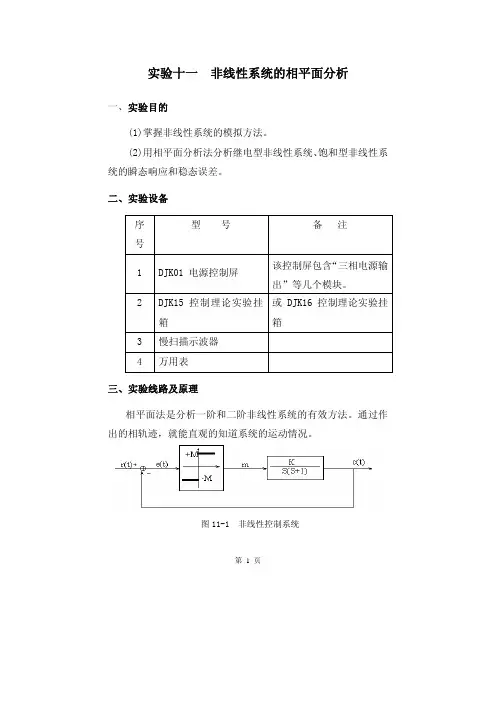
第 1 页实验十一 非线性系统的相平面分析一、实验目的(1)掌握非线性系统的模拟方法。

(2)用相平面分析法分析继电型非线性系统、饱和型非线性系统的瞬态响应和稳态误差。

二、实验设备 序号型 号备 注1DJK01 电源控制屏 该控制屏包含“三相电源输出”等几个模块。

2 DJK15控制理论实验挂箱或DJK16控制理论实验挂箱 3慢扫描示波器 4 万用表 三、实验线路及原理相平面法是分析一阶和二阶非线性系统的有效方法。

通过作出的相轨迹，就能直观的知道系统的运动情况。

图11-1 非线性控制系统第 2 页图11-2 理想继电器特性的模拟线路图图11-1为一具有理想继电器特性的非线性系统的框图，图11-2为理想继电器特性的具体接线参考图。

由图11-1得 Km C C =+。

,0,0m e m m e >⎧=⎨−<⎩则有），（），（。

0000<=++>=−+e KM C C e KM C C 令 r(t) = R，则 r(t)=0。

因为 r –c =e， 所以e= ­c 。

于是上式改写为），（），（。

0000<=−+>=++e KM e e e KM e e第 3 页初始条件 e（0）= r（0）- c（0）=R ，用等倾线法作出该系统的相轨迹如图11-3所示。

由图可见，系统从初始点A 出发，最后运动到坐标原点。

这不仅表明该系统稳定，而且由图还能确定系统的超调量δ%=0F/0A ×100%。

和稳定误差为零等性能指标。

图11-3四、思考题(1)实验中如何获得c 和c的信号？如何获得e 和e 的信号？ (2)试说明e ⎯e相轨迹和c ⎯c 相轨迹间的关系。

(3)你是如何从相平面图上得到超调量σρ和稳态误差ess 的？五、实验方法(1)用相轨迹分析图8-54所示的具有理想继电器特性的非线性系统在阶跃信号作用下的瞬态响应和稳态误差。

①根据图8-54设计相应的实验线路图，其中M=5V，K=1。

常微分方程中的相平面分析及其应用常微分方程（Ordinary Differential Equation, ODE）是数学中十分重要的一类方程，它描述的是一个未知函数的导数与某些已知函数的关系，常常出现在物理、工程、经济等领域中。

在解决ODE问题的过程中，相平面分析是一种重要的方法，通过画出相平面图，可以直观地理解ODE的行为，为解题提供了有力的工具。

本文将介绍相平面分析的基本思想及其应用。

一、相平面分析的基本思路相平面分析的基本思路是将ODE转化为相平面上的动力学问题。

具体地说，在ODE描述的函数空间中，选择一对函数变量，例如x1和x2，然后将ODE写成如下形式：dx_1/dt = f_1(x_1, x_2, t)dx_2/dt = f_2(x_1, x_2, t)其中f1和f2是已知函数。

将上述方程看作二维平面上的向量场，即使它在三维空间中，我们可以将其中一个变量t看做参数，得到一个二维平面上的向量场。

然后，在相平面上选择初值点，并以此为基础，在这个平面上跟踪ODE解的轨迹。

这些轨迹放在相平面上就构成了相平面分析的基本对象-相轨。

通过分析相轨的性质，可以对ODE的行为进行深入理解。

例如，相轨是否收敛到某一个点，如果是，那么该点就是ODE解的稳定平衡点。

相轨的形状、大小和数量等特征都可以揭示解的行为，这使得相平面分析成为一种非常有用的数学工具。

二、相平面分析在ODE求解中的应用1. 稳定性分析相平面分析最常见的应用之一是稳定性分析。

稳定性是指ODE 解的行为对初值点的选取是否敏感。

换句话说，如果一个ODE的解对初值点的微小扰动非常敏感，那么我们可以说该ODE是不稳定的。

如果初始条件发生微小变化时，ODE解的行为发生了显著改变，解的稳定性就不存在。

相反，如果初始条件变化很小，而ODE解的行为差异很小，我们就说ODE是稳定的。

假设ODE有一个稳定点x*，那么我们需要知道该ODE解是如何接近x*的。

7-5 非线性控制系统的相平面分析一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在ee -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e eT +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

应当指出，特征方程式的根确定了奇点的性质，在v v ee -平面上的奇点的位置是坐标原点，而在e e -平面上奇点坐标为)0,(0K V 点。