8-1已知具有理想继电器的非线性系统如图8-1所示,试用相平面法分析

·43·第8章 非线性控制系统的分析例题解析例8-1 设非线性系统具有典型结构，试用等效增益概念分析具有死区的三位置理想继电特性(见图8-1(a))对系统稳定性的影响。

图8-1 稳定性分析解：由等效增益定义x y K /=知，等效增益曲线如图8-1(b)所示，其中∆=/M K m 。

设系统不存在非线性时，临界稳定增益为K c ，于是① 若K c >K m ，如图8-1(b)所示，则因实际增益小于临界增益K c ，所以系统稳定 ② 若K c <K m ，如图8-1(c )所示，其中x 0=M./K c ，则当x<x 0时，因m K K >，系统不稳定，x 发散；当x 增加至使x >x 0时，此时m K K <，系统稳定，x 收敛；当x 减小至使x <x 0时，重复上述过程。

可见，在这种情况下，系统将出现以x 0为振幅的自激振荡。

③ 原系统加入具有死区的理想三位置继电特性后，改善了系统的稳定性。

不论原系统是否发散，现系统都不会发散，但可能产生一个以x 0为振幅的自激振荡。

例8-2 试求图8-2所示非线性环节的描述函数。

（a ） （b ）·44·图 8-2 非线性环节解：（1）对于图8-2（a ），因为t X x x y ωsin ,3==且单值奇对称，故A1＝03204320432043sin 4sin 1sin 11X t td X t d t X t td y B ====⎰⎰⎰πππωωπωωπωωπ21143)(X X A j X B X N =+=图 8-3（2）对于图8-2（b ），因为图示非线性可以分解为图8-3所示两个环节并联，所以 K XMX N X N X N +=+=π4)()()(21 例8-3 试将图8-4（a ），（b ）所示系统归化为一个非线性部分和一个线性部分串联的典型结构。

（a ） （b ）图 8-4解：（1）G 1与G 2是小回路的负反馈，则2111G G G G +=从而得典型结构，见图8-5。

第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dtyd m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （3） 2)()(R s Uc s I =（4） 联立式（3）、（4），可解得：CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++ 2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

解：
所以，可控子系统为：
不可控子系统为：
8-27系统各矩阵同题8-26，试求可观测子系统与不可观测子系统的动态方程。
解：利用9-27的对偶关系实现：
可观子系统：
不可观子系统：
8-28设系统状态方程为 。说明可否用状态反馈任意配置闭环极点，若可以，求状态反馈矩阵，使闭环极点位于 ，并画出状态变量图。
解：
第八章 线性系统的状态空间分析与综合
练习题及答案
8-1已知电枢控制的直流伺服电机的微分方程组及传递函数
+
⑴设状态变量 ， ， 及输出量 ，试建立其动态方程;
⑵设状态变量 及 ,试建立其动态方程。
解：
（1）由题意可知： ，
由已知
可推导出
由上式，可列动态方程如下
+
y =
（2）由题意可知：
可推导出
可列动态方程如下
取
则
验证：
验证完毕。
故可控标准型实现对应的 阵为：
8-25已知系统传递函数为 ，试写出系统可控、不可观测，可观测，不可控，不可控、不可观测的动态方程。
解：
传递函数有零极点对消，因此不可控或不可观。
可控、不可观方程：
可观测、不可控方程：
不可控、不可观测方程：
8-26已知系统动态方程各矩阵为：
试求可控子系统与不可控子系统的动态方程。
解： =
，系统可控
，系统可观测。
令：
即：
解得：
8-32已知系统动态方程各矩阵为
试判别系统的可观测性；设计 维观测器，并使所有极点配置在 。
解：检查可观测性：
，可观测。设计 维降维观测器：
构造 阵，求 。
经 变换后系统方程为：

19
8.2 描 述 函 数 法 8.2.1 描述函数的基本概念
设非线性环节的输入为 x(t)＝A sinωt
一般情况下，非线性环节的稳态输出y(t)是非正弦周期信号。 将y(t)用傅氏级数表示为
y t A0 An cos nt+Bn sin nt =A0 Yn sin nt+n
n =1
n =1
kx，
x ≤a
y Msignx， x ＞a
2
图8-1 饱和非线性特性
3
2． 死区特性
死区又称不灵敏区，如图8-2所示。其输入与输出之间关
系的表达式为
0，
x ≤Δ
y k x Δsignx， x ＞Δ
式中，Δ为死区范围； k为线性段的斜率。
当输入信号小于Δ时，对系统来说，虽然有输入但无输
出，只有当|x|＞Δ时才有输出，这时，输出与输入之间为
第八章 非线性控制系统分析
8.1 非线性系统的基本概念 8.2 描述函数法 8.3 相平面法 8.4 Matlab应用实例
1
8.1 非线性系统的基本概念 8.1.1 典型非线性特性
控制系统中含有本质非线性环节，如果这些本质非线性特 性能用简单的折线来描述，则称为典型非线性特性。
1. 饱和特性 饱和特性是一种常见的非线性特性，如图8-1所示。其数 学表达式为
最后指出，这种方法只适用于单个的非线性元件，如果有 两个以上的非线性元件，则必须把它们合并为一个模块，否则 第二个元件的输入就不会是正弦波。
22
8.2.2 典型非线性特性的描述函数 1． 死区特性 在具有死区的元件中，当输入在死区的幅值范围内时
就没有输出。图8-6所示为死区非线性特性及其输入、输出波 形。

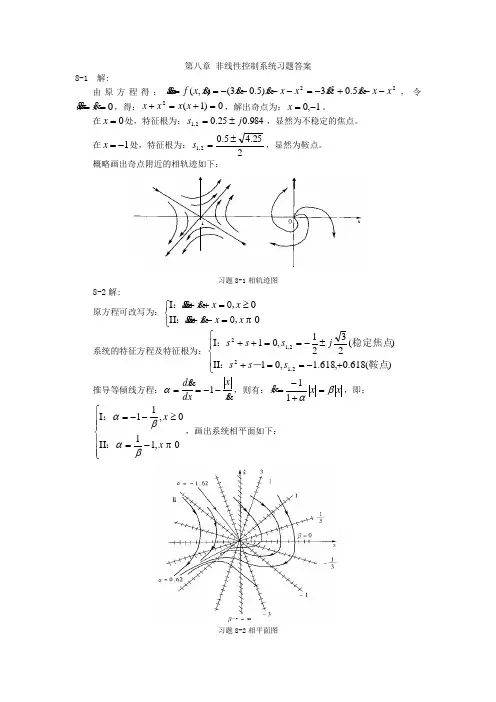
第八章 非线性控制系统习题答案8-1 解:由原方程得：2225.03)5.03(),(x x x x x x x x x x f x--+-=----== ，令0==x x，得：0)1(2=+=+x x x x ，解出奇点为：1,0-=x 。

在0=x 处，特征根为：984.025.02,1j s ±=，显然为不稳定的焦点。

在1-=x 处，特征根为：225.45.02,1±=s ，显然为鞍点。

概略画出奇点附近的相轨迹如下：-1习题8-1相轨迹图8-2解:原方程可改写为：⎩⎨⎧=-+≥=++0II 0Ix x x x x x x x 0,：0,：系统的特征方程及特征根为：⎪⎩⎪⎨⎧+-==+±-==++)(618.0,618.1,01II )(2321,01I 2,122,12鞍点－：稳定焦点：s s s js s s 推导等倾线方程：xx dx xd --==1α，则有：x x xβα=+-=11 ，即： ⎪⎪⎩⎪⎪⎨⎧-=≥--=0,11II 0,11I x x βαβα：：，画出系统相平面如下：习题8-2相平面图8-3 （1）解：相平面上任一点的相轨迹斜率为：x xxdxx dsin+-=，由=dxx d，得：),2,1,0(±±==kkxπ，因此在相平面的x轴上，),2,1,0(±±==kkxπ的点均为奇点。

在x轴上满足),2,1,0(2±±==kkxπ的所有奇点附近，由泰勒级数展开来验证这类奇点为稳定焦点。

在x轴上满足),2,1,0()12(±±=+=kkxπ的所有奇点附近，由泰勒级数展开来验证这类奇点为鞍点。

绘制相轨迹如下图所示：习题8-3（1）相轨迹图（2）解：原方程可改写为：⎩⎨⎧=-≥=+IIIxxxxxx0,：0,：系统的特征方程及特征根为：⎪⎩⎪⎨⎧±==±==+)(1,01II)(,01I2,122,12鞍点－：中心点：ssjss推导等倾线方程：⎪⎪⎩⎪⎪⎨⎧≥11xxxxxx,＝,－＝αα，画出系统相平面如下：习题8-3（2）相轨迹图（3）解：令0==xx，得0sin=x，得出系统的奇点：,2,,0ππ±±=x当,2,1,02±±==kx，κπ时，令2xx+=κπ，可以验证奇点,2,1,02±±==kx，κπ为中心点。

参考答案一、填空题1. 非本质；本质2. 自持振荡3. 初始条件；输入信号大小4. 饱和非线性；死区非线性；间隙非线性；继电器非线性5. 不稳定6. 稳定；不稳定；半稳定7. 自左向右；自右向左 二、分析与计算题1. 求3()()y t ax t =的描述函数。

解：由于3()()y t ax t =是单值奇函数，所以其傅里叶级数展开式中A 0=0、A 1=0、φ1=0，将()sin x t A t ω=代入B 1的计算公式，可得2102330340320320303031()sin 1sin sin 2sin 21cos 2()2212cos 2cos 241cos 412cos 22242311(cos 2cos 4)828231(sin 284B y t td taA t td t aA td t aA t d t aA t t d t tt aA d t aA t t d t aA πππππππωωπωωωπωωπωωπωωωπωωωπωωωπππ===-=-+=+-+==-+=-⎰⎰⎰⎰⎰⎰⎰31sin 4)003234t t aA ππωω+=所以32133()44B aA N A aA A A ===2．设具有滞环继电器非线性特性的非线性系统结构如题图8.1所示，已知b =1，a =0.3，试判断系统是否存在自持振荡，若存在，则求出自持振荡的幅值和频率。

题图8.1解：具有滞环的继电器非线性特性的描述函数为24()j()abN A A a Aπ=≥其描述函数负倒数特性为1j ()()4a A a N A bπ-=≥ 可见，描述函数负倒数特性的虚部为常数4a b π-，即1()N A -曲线为一条虚部为4abπ-的直线。

由于10()(21)(0.41)G s s s =++，所以222222222210(j )(2j 1)(0.4j 1)10(12j )(10.4j )(14)(10.16)10(1 2.4j 0.8)(14)(10.16)10824j (14)(10.16)(14)(10.16)G ωωωωωωωωωωωωωωωωω=++--=++--=++-=-++++由以上可知，1()N A -曲线与(j )G ω必有交点，而且交点为稳定的，因此会产生自持振荡。

7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。

但是，我们在介绍非线性系统的分析方法之前，先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。

因为许多非线性元件特性一般都可分段用线性方程来表示，所以非线性控制系统也可以用分段线性系统来近似。

一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在e e -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e e T +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

−
j
900
⎥ ⎥
=
⎢ ⎢0.494e
j 2550
⎥ ⎥
1 ⎥⎦⎢⎣2e j1350 ⎥⎦
⎢⎣0.195e
j1350
⎥ ⎦
8-13 试画出图 8-62 所示电力系统 k 点发生接地短路时的正序、负序和零序等值网络。
图 8-62 习题 8-13 附图
解：正序、负序、零序等值网络见下图 a)、b)、c)。
（3）k 点发生 a、c 两相接地短路时
Ib1
=
j( X 1∑
E1Σ
=
+ X 2∑ // X 0∑ )
j1 j(0.202 + 0.214 // 0.104)
= 3.677
Ib2
=
−
X 0∑ X2∑ + X0∑
Ib1
=
−
0.104 0.214 + 0.104
× 3.677
=
−1.203
Ib0
=
−
X 2∑ X2∑ + X0∑
Ib1
=
− 0.214 × 3.677 0.214 + 0.104
=
−2.474
U b1 = U b2 = U b0 = − jX 2∑ Ib2 = − j0.214 × (−1.203) = j0.257
Ib = 0
Ic = a 2 Ib1 + aIb2 + Ib0 = e j240° × 3.677 − e j120° ×1.203 − 2.474 = 5.624e− j131.29° Ia = aIb1 + a2 Ib2 + Ib0 = e j120° × 3.677 − e j240° ×1.203 − 2.474 = 5.624e j131.29° Ub = 3Ub1 = 3× j0.257 = j0.771 U a = U c = 0

8非线性控制系统前面几章讨论的均为线性系统的分析和设计方法，然而，对于非线性程度比较严重的系统，不满足小偏差线性化的条件，则只有用非线性系统理论进行分析。

本章主要讨论本质非线性系统，研究其基本特性和一般分析方法。

8.1非线性控制系统概述在物理世界中，理想的线性系统并不存在。

严格来讲，所有的控制系统都是非线性系统。

例如，由电子线路组成的放大元件，会在输出信号超过一定值后出现饱和现象。

当由电动机作为执行元件时，由于摩擦力矩和负载力矩的存在，只有在电枢电压达到一定值的时候，电动机才会转动，存在死区。

实际上，所有的物理元件都具有非线性特性。

如果一个控制系统包含一个或一个以上具有非线性特性的元件，则称这种系统为非线性系统，非线性系统的特性不能由微分方程来描述。

图8-1所示的伺服电机控制特性就是一种非线性特性，图中横坐标u为电机的控制电压，纵坐标为电机的输出转速，如果伺服电动机工作在A1OA2区段，则伺服电机的控制电压与输出转速的关系近似为线性，因此可以把伺服电动机作为线性元件来处理。

但如果电动机的工作区间在B1OB2区段•那么就不能把伺服电动机再作为线性元件来处理，因为其静特性具有明显的非线性。

8.1.1控制系统中的典型非线性特性组成实际控制系统的环节总是在一定程度上带有非线性。

例如，作为放大元件的晶体管放大器，由于它们的组成元件（如晶体管、铁心等）都有一个线性工作范围，超出这个范围，放大器就会出现饱和现象；执行元件例如电动机，总是存在摩擦力矩和负载力矩，因此只有当输入电压达到一定数值时，电动机才会转动，即存在不灵敏区，同时，当输入电压超过一定数值时，由于磁性材料的非线性，电动机的输出转矩会出现饱和；各种传动机构由于机械加工和装配上的缺陷，在传动过程中总存在着间隙，等等。

实际控制系统总是或多或少地存在着非线性因素，所谓线性系统只是在忽略了非线性因素或在一定条件下进行了线性化处理后的理想模型。

常见典型非线性特性有饱和非线性、死区非线性、继电非线性、间隙非线性等。

第一部分信号系统实验一常用信号的观察一、实验目的1.了解常用信号的波形和特点。

2.了解相应信号的参数。

3.学习示波器的使用。

二、实验设备1．THBCC-1型信号与系统²控制理论及计算机控制技术实验平台2．双踪慢扫描示波器1台3．PC机（安装数字信号发生器的软件），串口通信线一根。

三、实验内容1．观察常用的信号，如：正弦波、方波、三角波、锯齿波及一些组织函数波形如y=sin(n ³x)+cos(m³x)。

2．用示波器测量信号，读取信号的幅度和频率，并用坐标纸上记录信号的波形。

四、实验原理说明描述信号的方法有多种，可以是数学表达式（时间的函数），也可以是函数图形（即为信号的波形）。

对于各种信号可以分为周期信号和非周期信号；连续信号和离散信号等。

五、实验步骤1．连接数字信号发生器的串口通信线，打开数字信号发生器的电源。

2．运行上位机的波形发生器软件，选择串口和波特率，然后选择波形，点击发送数据，用示波器观察输出的波形。

3．选择不同的频率，观察输出波形的变化。

六、实验报告1．根据实验测量的数据，绘制各个信号的波形图，并写出相应的数学函数表达式。

实验二 零输入、零状态及完全响应一、实验目的1．通过实验，进一步了解系统的零输入响应、零状态响应和完全响应的原理。

2．掌握用简单的R-C 电路观测零输入响应、零状态响应和完全响应的实验方法。

二、实验设备1．THBCC-1型 信号与系统²控制理论及计算机控制技术实验平台 2．双踪慢扫描示波器1台三、实验内容1．连接一个能观测零输入响应、零状态响应和完全响应的电路图（参考图2-1）。

2．分别观测该电路的零输入响应、零状态响应和完全响应的动态曲线。

四、实验原理1.零输入响应、零状态响应和完全响应的模拟电路如图2－1所示。

图2-1 零输入响应、零状态响应和完全响应的电路图2.合上图2-1中的开关K1，则由回路可得iR+Uc ＝E (1)∵ i ＝C dt dUC ，则上式改为＝E c U dtc dURC + (2) 对上式取拉式变换得：RCU C （S ）-RCU C （0）+U C （S ）＝S15∴RC 1S 5RC 1S 15S15＝1RCS （0）RCU 1）S（RCS 15(S）＝c U c ++⎪⎪⎪⎪⎭⎫⎝⎛+-+++，其中5V (0)U C =tRC 1-t RC 1-e e 1（t）＝15c U 5+⎪⎪⎭⎫ ⎝⎛-(3)式(3)等号右方的第二项为零输入响应，即由初始条件激励下的输出响应；第一项为零状态响应，它描述了初始条件为零（Uc（0）=0）时，电路在输入E=15V作用下的输出响应，显然它们之和为电路的完全响应，图2-2所示的曲线表示这三种的响应过程。

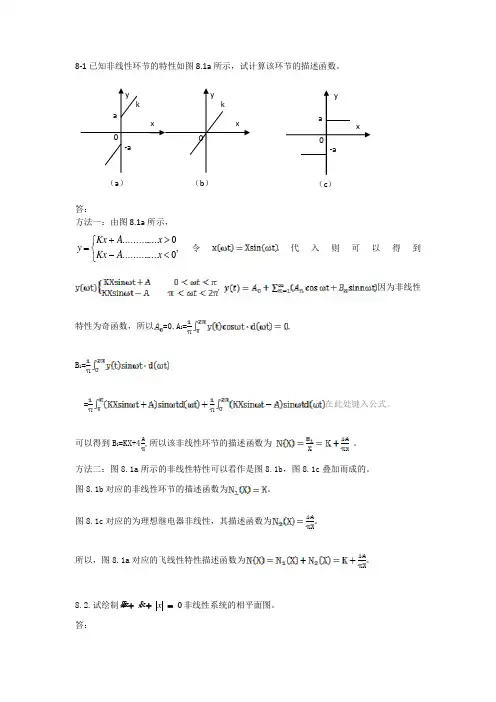
8-1已知非线性环节的特性如图8.1a 所示，试计算该环节的描述函数。

答：方法一：由图8.1a 所示，,0...............0...............⎩⎨⎧<->+=x A Kx x A Kx y 令代入则可以得到, 因为非线性特性为奇函数，所以=0,A 1=,B 1==在此处键入公式。

可以得到B 1=KX+4,所以该非线性环节的描述函数为 。

方法二：图8.1a 所示的非线性特性可以看作是图8.1b ，图8.1c 叠加而成的。

图8.1b 对应的非线性环节的描述函数为。

图8.1c 对应的为理想继电器非线性，其描述函数为。

所以，图8.1a 对应的飞线性特性描述函数为。

8.2.试绘制0=++x x x &&&非线性系统的相平面图。

答：y 0 -a a x k （a ） y 0 xk （b ） y（c ）0 -aa x由题意，此方程可以改写为：,开关线为x=0。

当x>0时，相轨迹方程对应的特征方程为+λ+1=0，，由可以得到.故奇点为稳定的焦点。

当x<0时，相轨迹方程对应的特征方程为+λ-1=0,,由可以得到此时的奇点为（0,0），奇点为鞍点，推导等倾线方程。

令=α，可以得到等倾线方程为,令等倾线的斜率为k ，即可以得到，得到,列写表格如下表所示。

K -3 -2 -10 1 2 3 +∞,8.3.系统方框图如图8-29所示，其中K>0，T>0。

当非线性元件N分别为理想继电特性;死区继电特性;滞环继电特性;带死区和滞环的继电特性，在cc&-相平面上绘制相平面图。

8-29系统方框图（1）具有死区的三位置继电特性线性部分的微分方程为当继电特性为具有死区的三位置继电特性时，上式可以写成分段微分方程为：C(t)r = 0- )1(+TssKN(e)e)开关线为,两条开关将相平面划分为三个线性区域，下面分区绘制相轨迹在区域，相轨迹方程为：类似于具有饱和特性的非线性控制系统时的讨论，像平面与该区域无奇点，相轨迹均渐进于的直线。

第八章习题8-1： 图（a ）所示输电系统，在f点发生接地短路，试绘出各序网络，并计算电源的组合电势∑E 和各序组合电抗∑1X 、∑2X 和∑0X 。

已知系统各元件参数如下：发电机G ：50MW ，8.0cos =ϕ，15.0=''dX ，18.02=X ，08.11=E 变压器T-1、T-2：60MVA ，V s %=10.5，中性点接地阻抗Ω=22n x负荷：X LD1=1.2, X LD2=0.35 线路L ：50km ，km x /4.01Ω=，103x x =解 （1）各元件参数标幺值计算。

选取基准功率B S =100MVA 和基准电压av B V V =，计算各元件的各序电抗的标幺值，计算结果标于各序网络图中。

发电机：24.08.0/5010015.01=⨯=G X 288.08.0/5010018.02=⨯=G X 变压器T-1、T-2：175.0601001005.1021=⨯==T T X X 中性点接地阻抗:607.137100222=⨯=n x 负荷LD ：8151002.11=⨯=LD X 333.21510035.02=⨯=LD X 输电线路L ：461.1371004.05021=⨯⨯=L X 383.4416.130=⨯=L X（2）制订各序网络正序和负序网络不包括中性点接地电抗和空载变压器T-2，因此，正序和负序网络中包括发电机G 、变压器T-1、负荷LD 以及输电线路L ,如图（b ）和（c ）所示。

由于零序电流不流经发电机和负荷，因此，零序网络中只包括变压器T-1、T-2和输电线路L ，如图（d ）所示。

（3）网络化简，求组合电势和各序组合电抗。

由图（b ）可得05.1824.0808.1=+⨯=∑E869.1461.1175.0)8//24.0(1=++=∑X由图（b ）和图（c ）可得892.1461.1175.0)333.2//288.0(2=++=∑X172.0175.0//)383.4821.4175.0(0=++=∑X8-2：如图（a ）所示电力系统，各元件参数如下：发电机G-1：100MW ，cos ϕ=0.85，223.0,183.02==''X X d；G-2：50MW ，cos ϕ=0.8，141.0=''d X ，172.02=X ；变压器T-1：120MVA ，V s %=14.2；T-2：63MVA ，V s %=14.5；输电线路L ：每回120km ，1015,/432.0x x km x =Ω=。

[例2—1]一条220kV的输电线,长180km，导线为LGJ—400(直径2.8cm),水平排列，相间距7m,求该线路的R，X，B,并画等值电路.解：电阻:电抗:电纳：等值电路：[例2-2]220kV架空线,水平排列,相间距7m，每相为分裂导线,计算直径21.88mm，分裂间距400mm，求每相单位长度的电阻、电抗和电纳.解:电阻:电抗:电纳:［例2-3]一长度为600 km 的500kV 架空线路,使用4×LGJQ—400 四分裂导线，。

试计算该线路的形等值电路参数。

解（1）精确计算。

计算形等效电路参数：（2)使用近似算法计算。

与准确计算相比，电阻误差-0.4％,电抗误差-0。

12%，电纳误差—0。

24％，本例线路长度小于1000km ，用实用近似公式计算已能够满足精确要求。

如果直接取这时，电阻误差达15%,电抗误差7％，电纳误差—3.4%,误差已较大。

例2－4 330kV架空线路的参数为试分别计算长度为100，200，300，400和500线路的π型等值参数的近视值，修正值和精确值。

解首先计算100km线路的参数(一）（二）修正参数计算（三) 精确参数计算计算双曲线函数.利用公式sh（x+jy)=shxcosy+jchxsinych（x+jy)=chxcosy+jshxsiny将之值代入，便得II型电路的精确参数为[例2—5］有一台SFL120000/110型的向10kV网络供电的降压变压器，铭牌给出的实验数据为：试计算归算到高压侧的变压参数。

解由型号知，各参数如下：例2-6 三相三绕组降压变压器的型号为SFPSL-120000/220，额定容量为120MVA/120MVA/60MVA，额定电压为：220kV/121kV/11kV,，, ，，，，，，求变压器归算到220kV 侧的参数，并作出等值电路。

解:（1)求各绕组的电阻同理可得:电阻计算如下：（2)求各绕组电抗电抗计算：变压器阻抗参数：(3)求导纳例2—7试计算2—15（a）所示输电系统各元件电抗的标幺值。

8-1 计算下列各式：(1) o o o 615440760∠-∠+∠- (2) (1033)(45)(64)73j j j j++-+ 解： (1) o o o 6154407605.8 1.553 3.064 2.571 3.56.0626.2367.089.43548.63oj j j j ∠-∠+∠-=+--+-=-=∠- (2)o(1033)(45)(64)34.4873.14 6.451.347.2133.69208.867.59737.6223.2o o oo j j j j ++-∠⨯∠⨯∠-==∠+∠8-2 若100060173o o A θ∠+∠=∠，试求A 和θ。

解：100/2173cos 173sin 2A jA j θθ++=+，实部和虚部分别相等。

1212100/2173cos 100200,3090173sin o o A A A θθθθ+=⎧==-⎧⎧⎪⇒⎨⎨⎨==-=⎩⎩⎪⎩ 8-7 (1)已知图题8-1(a)中，12()10cos(36.86),()6cos(120)o o i t t A i t t A ωω=+=+，求()i t ，并绘出向量图。

(2)已知图题8-1(b)中，12()80cos(36.86),()60cos(126.9)o o u t t V u t t V ωω=+=+，3()120cos(53.13)o u t t V ω=-求u()t ，并绘出向量图。

解 (1)变为向量形式，121036.86,6120o o m mI A I A =∠=∠ ，由KCL 的向量形式可得：()121036.86612012.2665.94o o o m m mI I I A A =+=∠+∠=∠ 反变换得：()12.26cos(65.94)o i t t A ω=+(2) 由KVL 得向量形式可得：()122o U U U U 8036.960126.912053.1100m m m mo o V V=++=∠+∠+∠-=8-11 已知图题8-2所示无源网络两端电压u(t)和电流i(t)各如下所示。

(−∞ , −1) 段，方向向左，分别绘于上图 (a) (b) 上。 N
对于图
(a) 所示情形，G (
jω )
与
−
1 N
无交点，非线性系统不会产生自持振荡，
该非线性系统也是稳定的；
对于图 (b) 所示情形，G ( jω ) 与 − 1 有两个交点，其中交点 A 是稳定交点，
N
该非线性系统会产生自持振荡。
2 时， N(A)取极值。
2
−1
= − π ≈ −0.39
N ( A) A= 2
8
2
( ) （4）计算自振参数
− 1 =G N ( A)
jωg
A1 = 12.72 ，A2 = 0.503
即：系统将产生自振，振荡角频率为 ωg = 1 rad s ，振幅为 A = 12.72
12
【解】（1）将系统方框图化为标准结构
分析可得， ∆1 = 0.5
11
得系统等效方框图为：
（2）绘出线性部分的 G ( jω)曲线
与负实轴的交点处，ωg = 1
G( jω) =
10
=5
ω ⋅ ( 1+ ω 2 )2 ω =ωg
−0.39
（3）绘出非线性部分的
−
1 N
曲线
计算可得，当 A =
2e0 =
解得：
∆1
=
∆ k
+α
4
习题8.4 设有非线性控制系统，其中非线性特性为斜率 k = 1的饱
和特性。当不考虑饱和特性时，闭环系统稳定。试分析该非线性控制系统 是否有产生自持振荡的可能性。 【解】不考虑饱和因素时，稳定的线性系统的开环频率响应形式有多种，例如：
AB
考虑饱和因素，斜率为 k = 1的饱和特性的 − 1 曲线分布在负实轴上

第七章非线性控制系统分析练习题及答案7-1设一阶非线性系统的微分方程为xx3 x试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解令x0得3(21)(1)(1)0xxxxxxx系统平衡状态x e0,1,1其中：x0：稳定的平衡状态；ex1,1：不稳定平衡状态。

e计算列表，画出相轨迹如图解7-1所示。

x-2-11301312x-600.3850-0.38506x112010211图解7-1系统相轨迹可见：当x(0)1时，系统最终收敛到稳定的平衡状态；当x(0)1时，系统发散；x(0)1 时，x(t);x(0)1时，x(t)。

注：系统为一阶，故其相轨迹只有一条，不可能在整个x~x平面上任意分布。

7-2试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1)xxx0(2) x1x2xx122xx12解（1）系统方程为1:xxx0(x0):xxx0(x0)令xx0，得平衡点：x e0。

系统特征方程及特征根：132:ss10,sj(稳定的焦点)1,2222:ss10,s1.618,0.618(鞍点)1,2xf(x,x)xx, d xdxxxxdx dx 1xx,1xxx11I:1(x0)1II:1(x0)计算列表-∞-3-1-1/301/313∞x0:11-1-2/302-∞-4-2-4/3-1x0:11-1-4/3-2-4∞20-2/3-1用等倾斜线法绘制系统相平面图如图解7-2（a）所示。

2图解7-2（a）系统相平面图（2）xxx112①x22xx②12由式①：x2x1x1③式③代入②：(x1x1)2x1(x1x1)即x12x1x10④令x1x10得平衡点：x e0由式④得特征方程及特征根为2.4142ss2101,2（鞍点）0.414画相轨迹，由④式xx 11 d x1dxx12x1x1x 1 x1 2计算列表322.53∞11.52=1/(-2)∞210-1-2∞用等倾斜线法绘制系统相平面图如图解7-2（b）所示。

第八章 非线性控制系统分析练习题及答案8-2 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中：0=e x ：稳定的平衡状态；1,1+-=e x ：不稳定平衡状态。

计算列表，画出相轨迹如图解8-1所示。

可见：当x ()01<时，系统最终收敛到稳定的平衡状态；当x ()01>时，系统发散；1)0(-<x 时，x t ()→-∞; 1)0(>x 时，x t ()→∞。

注：系统为一阶，故其相轨迹只有一条，不可能在整个 ~xx 平面上任意分布。

8-3 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1) x xx ++=0 (5) ⎩⎨⎧+=+=2122112x x xx x x解 （1） 系统方程为x -2 -1 -13 0 131 2x-6 0 0.385 0 -0.385 0 6 x 11 2 01 0211图解8-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==，得平衡点：0e x =。

系统特征方程及特征根：21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解8-2（a ）所示。

图解8-2（a ）系统相平面图（5） xx x 112=+ ① 2122x x x+= ② 由式①： x xx 211=- ③ 式③代入②： ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点： x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s （鞍点） 画相轨迹，由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解8-2（b ）所示。