7-2相平面法
- 格式:ppt
- 大小:468.00 KB
- 文档页数:25
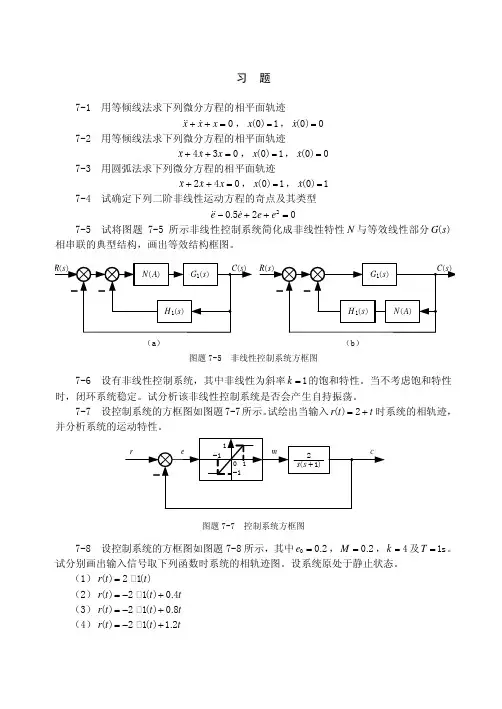
习题7-1用等倾线法求下列微分方程的相平面轨迹0x xx ++= ,0x =()1,0x = ()07-2用等倾线法求下列微分方程的相平面轨迹430x xx ++= ,0x =()1,0x = ()07-3用圆弧法求下列微分方程的相平面轨迹240x xx ++= ,01x =(),01x = ()7-4试确定下列二阶非线性运动方程的奇点及其类型20.520e ee e -++= 7-5试将图题7-5所示非线性控制系统简化成非线性特性N 与等效线性部分G s ()相串联的典型结构,画出等效结构框图。
(a )(b )图题7-5非线性控制系统方框图7-6设有非线性控制系统,其中非线性为斜率1k =的饱和特性。
当不考虑饱和特性时,闭环系统稳定。
试分析该非线性控制系统是否会产生自持振荡。
7-7设控制系统的方框图如图题7-7所示。
试绘出当输入2r t t =+()时系统的相轨迹,并分析系统的运动特性。
图题7-7控制系统方框图7-8设控制系统的方框图如图题7-8所示,其中00.2e =,0.2M =,4k =及1s T =。
试分别画出输入信号取下列函数时系统的相轨迹图。
设系统原处于静止状态。
(1)21r t t = ()()(2)210.4r t t t =-+ ()()(3)210.8r t t t =-+ ()()(4)21 1.2r t t t=-+ ()()图题7-8控制系统方框图7-9设控制系统采用非线性反馈时的方框图如图题7-9所示。
试绘制系统响应1r t R t = ()()的相轨迹图,其中R 为常值。
图题7-9非线性反馈系统方框图7-10设控制系统的方框图如图题7-10所示。
试绘制 (1)1r t R t = ()() (2)1r t R t tυ=+ ()()时e e- 平面相轨迹图,R ,υ为常值及000c c ==()()。
图题7-10控制系统方框图图题7-11控制系统方框图7-11设控制系统的方框图如图题7-11图示。

第七章非线性系统第一节,非线性的大体概念一,非线性模型组成:非线性环节+线性环节二,分类从形状特性上分:饱和、死区、回环、继电器a,饱和x三,特点:稳固性与结构,初始条件有关;响应不能用叠加原理四,分析方式相平面法(实际限于二阶非线性系统)较精准,因高阶作用太复杂描述函数法:近似性,高阶系统也很方便1,2四,滞环特性(间隙)7—2 二阶线性和非线性系统相平面法分析一、相平面法大体概念要完全地描述二阶的系统时域行为,至少要用两个变量(状态变量)。
可选x(t) 和)(t x作为状态变量。
1. 相平面:以横坐标表示X ,以纵坐标x组成一个直角坐标系, 2. 相轨迹:相平面上的点随时刻转变刻画出来的曲线称为相轨迹。
3. 相平面图:相平面和想轨迹曲线簇组成相平面图。
4. 想平面法:用相图表示非线性二阶系统进程的方式成相平面法,5. 相平面发局限性在于只适用在定常系统,系统输入只适限于阶跃和斜坡。
举例:例8—1 某弹簧——质量运动系统。
m —质量,k —弹性系数解:描述系统运动的微分方程为:直接微分法。
方程x ∙∙+x=0 可写成 x ∙dx ∙/dx=--x分离变量x ∙dx=--xdx 代入初始条件∫x ∙dx ∙=--∫xdx即 x+x=Xo 与上法结果相同。
分析:等幅振荡特性能够用相轨迹表征 ,相轨迹为闭合曲线。
一. 奇点1. 概念:相轨迹方程dx`/dx 为不定值的点dy/dx=0/04.奇点类型1) 稳固核心(-1<ζ<0) 相轨迹从原点向外发散,自由运动不收敛平稳点,是周期性增幅振荡二. 极限环分类相平面上孤点的闭和曲线称为极限环,与初始条件无关. 极限环表示对应于时域中有确信振幅和频率的振荡,极限环包括 稳固极限环 不稳固极限环 半稳固极限环稳固极限环:极限环外部和内部起始的相轨迹都渐进趋向于那个极限环,任何较小的扰动使系统离开极限环后,最后回到环上。
不稳固极限环、半稳固极限环不能产生自振荡,环内相轨迹发散、极限环外相轨迹收拢极限环7—3非线性系统的相平面分析第一依照非线性特性的分段情形,用几条分界限将相 划分为几个现行区域1) 然后依照系统的结构图别离列写各区域的线性微分方程式2) 并应用线性系统相平面分析的方式和结论,绘出各区域的相轨迹3) 依照系统状态转变的持续性,在各区域的交壤限上,将响轨迹彼此衔接成持续曲线,即组成完整的线性系统相图实奇点:每一个区域内有一个奇点,若是那个奇点在本区域之内,这种奇点称实奇点 虚奇点:若是奇点落在本区域之外,称虚奇点说明该区域相轨迹不可能聚集于虚奇点. 二阶非线性系统中,只可能有一个实奇点,而与那个实奇点所在区域邻接的所有其它区域都可能有虚奇点操纵系统分析例: 饱和特性的非线性操纵系统,用相平面法分析系统的阶跃响应和斜坡响应解:系统线性部份c(s)/x(s)=s+1) ``+c`\ e=r-c非线性部份:10e |e|<1x= 10 e>1-10 e<-1阶跃响应r=Rx1(t),当t>0+时r``(t)=r`(t), r=R e`=-c`, e``=-c``描述系统误差的方程为``+e`+=0x=10e |e|<=1x=10 e>1x=-10 e>1即为方程线性方程,在相平面上,e=+-1的两条直线把相平面划分为三个区域,1) 关于1区,系统线性微分方程为``+e`+=0de`/de=-e` 相轨迹方程。


7.2 相平面法相平面法是一种在时域中求解二阶微分方程的图解法。
它不仅能分析系统的稳定性和自振荡,而且能给出系统运动轨迹的清晰图像。
相平面法一般适用于二阶非线性系统的分析。
7.2.1 相平面的基本概念1. 相平面和相轨迹设一个二阶系统可以用下面的常微分方程),(=+xxfx(7-1)来描述。
其中),(xxf 是x和x 的线性或非线性函数。
在一组非全零初始条件下()0(x 和)0(x不全为零),系统的运动可以用解析解)(tx和)(tx 描述。
如果取x和x 构成坐标平面,则系统的每一个状态均对应于该平面上的一点,这个平面称相平面。
当t变化时,这一点在x-x 平面上描绘出的轨迹,表征系统状态的演变过程,该轨迹就叫做相轨迹(如图7-8(a)所示)。
相平面和相轨迹曲线簇构成相平面图。
相平面图清楚地表示了系统在各种初始条件下的运动过程。
例如,研究以方程22=++xxxωξω(7-2)描述的二阶线性系统在一组非全零初始条件下的运动。
当0=ξ时式(7-2)变为2=+xxω(7-3)初始条件为)0(xx=,)0(xx=,方程(7-3)对应有一对虚根,即ωjp±=-2,1式(7-3)的解为图7-8 相轨迹)sin(ϕω+=tAx(7-4)式中,2220ωxxA+=,arctanxxωϕ=设x为描述二阶线性系统的一个变量,取x为描述系统的另一状态变量,即)cos(ϕωω+==tAdtdxx (7-5)从式(7-4)、式(7-5)中消去变量t,可得出系统运动过程中两个状态变量的关系为222)(Axx=+ω这是一个椭圆方程。
椭圆的参数A取决于初始条件x和x 。
选取不同的一组初始条件,可得到不同的A,对应相平面上的相轨迹是不同的椭圆,这样便得到一个相轨迹簇。
0=ξ时的相平面图如图7-9所示,表明系统的响应是等幅周期运动。
图中箭头表示时间t增大的方向。
2.相轨迹的性质相平面的上半平面中,0>x ,相迹点沿相轨迹向x轴正方向移动,所以上半部分相轨迹箭头向右;同理,下半相平面0<x ,相轨迹箭头向左。

7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。
但是,我们在介绍非线性系统的分析方法之前,先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。
因为许多非线性元件特性一般都可分段用线性方程来表示,所以非线性控制系统也可以用分段线性系统来近似。
一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。
若系统开始处于平衡状态。
试求系统在阶跃函数)(1)(0t R t r ⋅= 作用下,在e e -平面上的相轨迹。
建立系统微分方程式,由图示系统可得Ke c cT =+ 因为c r e -=,代入上式得r r T Ke e e T +=++ (7-31) 对于->⋅=0),(1)(0t t R t r 时,0)()(==t r t r因此上式可写成0=++Ke e e T (7-32)方程(7-32)与(7-22)式相仿。
因为假设系统开始处于平衡状态,所以误差信号的初始条件是0)0(R e =和0)0(=e。
e e -平面上的相轨迹起始于)0,(0R 点,而收敛于原点(系统的奇点)。
当系统特征方程的根是共轭复数根,并且位于左半平面时,其相轨迹如图7-39(a)所示。
根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹,如图7-39(b)所示。
由图7-39可见,欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。
因为e e -平面相轨迹最终到原点,即奇点;所以在cc -平面上相轨迹最终到达0R c =的稳态值,则奇点坐标为)0,(0R 。
2、斜坡响应 对于斜坡输入t V t r 0)(=;当0>t 时,)(t r 的导数0)(V t r= 及0)(=t r 。
因此,方程(7-31)可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0,代入上式,则有0V Ke ee T =++ννν (7-33) 在v v ee -平面上,方程(7-33)给出了相平面图与在e e -平面上方程(7-32)给出的相平面图是相同的。




第七章 非线性控制系统分析练习题及答案7-1 设一阶非线性系统的微分方程为3x x x+-=& 试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解 令 x =0 得-+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中:0=e x :稳定的平衡状态;1,1+-=e x :不稳定平衡状态。
计算列表,画出相轨迹如图解7-1所示。
可见:当x ()01<时,系统最终收敛到稳定的平衡状态;当x ()01>时,系统发散;1)0(-<x 时,x t ()→-∞; 1)0(>x 时,x t ()→∞。
注:系统为一阶,故其相轨迹只有一条,不可能在整个 ~x x 平面上任意分布。
7-2 试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1) x x x ++=0 (2) ⎩⎨⎧+=+=2122112x x xx x x &&解 (1) 系统方程为x -2 -1 -13 0 13 1 2x -6 0 0.385 0 -0.385 0 6 x11 2 0 1 0211图解7-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x &&&&&&令0x x ==&&&,得平衡点:0e x =。
系统特征方程及特征根:21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxx x xdx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解7-2(a )所示。

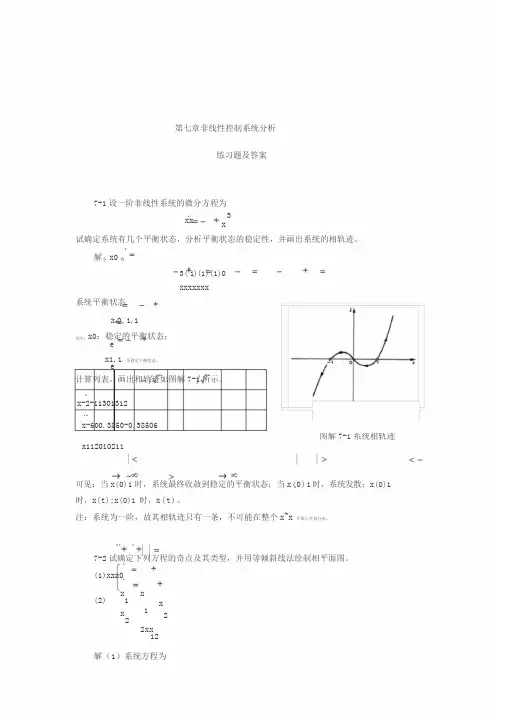
第七章非线性控制系统分析练习题及答案7-1设一阶非线性系统的微分方程为xx3 x试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解令x0得3(21)(1)(1)0xxxxxxx系统平衡状态x e0,1,1其中:x0:稳定的平衡状态;ex1,1:不稳定平衡状态。
e计算列表,画出相轨迹如图解7-1所示。
x-2-11301312x-600.3850-0.38506x112010211图解7-1系统相轨迹可见:当x(0)1时,系统最终收敛到稳定的平衡状态;当x(0)1时,系统发散;x(0)1 时,x(t);x(0)1时,x(t)。
注:系统为一阶,故其相轨迹只有一条,不可能在整个x~x平面上任意分布。
7-2试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1)xxx0(2) x1x2xx122xx12解(1)系统方程为1:xxx0(x0):xxx0(x0)令xx0,得平衡点:x e0。
系统特征方程及特征根:132:ss10,sj(稳定的焦点)1,2222:ss10,s1.618,0.618(鞍点)1,2xf(x,x)xx, d xdxxxxdx dx 1xx,1xxx11I:1(x0)1II:1(x0)计算列表-∞-3-1-1/301/313∞x0:11-1-2/302-∞-4-2-4/3-1x0:11-1-4/3-2-4∞20-2/3-1用等倾斜线法绘制系统相平面图如图解7-2(a)所示。
2图解7-2(a)系统相平面图(2)xxx112①x22xx②12由式①:x2x1x1③式③代入②:(x1x1)2x1(x1x1)即x12x1x10④令x1x10得平衡点:x e0由式④得特征方程及特征根为2.4142ss2101,2(鞍点)0.414画相轨迹,由④式xx 11 d x1dxx12x1x1x 1 x1 2计算列表322.53∞11.52=1/(-2)∞210-1-2∞用等倾斜线法绘制系统相平面图如图解7-2(b)所示。
第七章7-1 什么是非线性系统?它是什么特点?7-2 常见的非线性特征有哪些?7-3 非线性系统的分析设计方法有哪些?7-4 描述函数分析法的实质是什么?试描述函数的概念及其求取方法。
7-5 试述相平面分析法的实质。
为什么它是分析二阶系统的有效方法?7-6 试确定3xy表示的非线性元件的描述函数。
7-7 一放大装置的非线性特性示于图p7-1,求其描述函数。
7-8 图p7-2为变放大系数非线性特征,求其描述函数。
7-9 求图p7-3所示非线性环节的买书函数。
7-10 某死区非线性特性如图p7-4所示,试画出该环节在正弦输入下的输出波形,并求出其描述函数N{A}。
7-11 图p7-5给出几个非线性特性。
试分别写出其基准描述函数公式,并正在复平面上大致画出其基准描述函数的负倒数特性》7-12 判断图p7-6所示各系统是否稳定?-1/N。
与K。
W(jw)的交点是稳定工作点还是不稳定工作点?解:(a)是稳定工作点(b)是稳定工作点(c)a点不是稳定工作点b点是稳定工作点(d)不是稳定工作点(e)是稳定工作点7-13 图p7-7所示为继电器控制系统的结构图,其线性部分的传递函数为 )11.0)(15.0)(1(10)(+++=s s s s W 试确定自持振荡的角频率和振幅。
解:该系统非线性部分为具有滞环的两位置继电器,其描述函数为(见教材P343 公式(7-25)):)(414)(22h A A Mh jA h A M A N ≥-⎪⎭⎫⎝⎛-=ππ则)(414141*********)(1222222222h A M h j A h M A A h j A h M A A h A h A h jA h M A A h j A h A h j A h A h jA h M AA h jA h MAA N ≥-⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛--=-⎪⎭⎫⎝⎛-=-ππππππ由图可得:2=M ,1=h 代入到)(1A N -中,)(8118)(12h A j A A A N ≥-⎪⎭⎫ ⎝⎛--=-ππ线性部分相频为:)1.01)(5.01)(1()05.06.165.01(10)1.01)(5.01)(1()1.01)(5.01)(1(10)1.01)(5.01)(1)(11.0)(15.0)(1()1.01)(5.01)(1(10)11.0)(15.0)(1(10)(222223222222ωωωωωωωωωωωωωωωωωωωωωωωωω+++---=+++---=---+++---=+++=j j j j j j j j j j j j j j j j j j W因为)(ωj W 曲线与)(1A N -曲线相交,则虚部8)1.01)(5.01)(1(5.016222223πωωωωωj j j -=+++--即8)1.01)(5.01)(1(5.016222223πωωωωω=++++ ωωωωω2832.6194.0126.12625.00025.03246+=+++即012832.626.1194.02625.00025.02346=+-+-+ωωωωω 解上述方程得到:1645.01=ω,4256.22=ω00198.1494.07.434.91645.01.0arctan 1645.05.0arctan 1645.0arctan )(-=---=⨯-⨯--=ωϕ显然不符合题义。
第7章 非线性系统的分析1.试计算并绘制下列各微分方程的相平面图。
解:(1)求得运用积分法解得相轨迹方程为其相轨迹如图7-1所示。
(2)求得运用积分法解得相轨迹方程为其相轨迹如图7-2所示。
图7-1 系统的相轨迹 图7-2 系统的相轨迹(3)求得令切线斜率,则可得等倾线方程为,即可见等倾线为一簇水平线。
①当α=0时,,则该等倾线亦为一条相轨迹,因相轨迹互不相交,故其他相轨迹均以此线为渐近线。
②当α→∞时,,表明相轨迹垂直穿过x轴。
③当α→-1/T时,,说明相平面上下无穷远处的相轨迹斜率为-1/T。
最后根据等倾线作图法可得其概略相轨迹如图7-3所示。
图7-3 系统的概略相轨迹(4)求得令切线斜率,则可得等倾线方程为,即可见等倾线为一簇水平线。
①当α=0时,x=M,则该等倾线亦为一条相轨迹,因相轨迹互不相交,故其他相轨迹均以此线为渐近线。
②当α→∞时,,表明相轨迹垂直穿过x轴。
③当α→-1/T时,,说明相平面上下无穷远处的相轨迹斜率为-1/T。
最后根据等倾线作图法可得其概略相轨迹,如图7-4所示。
图7-4 系统的概略相轨迹(5)求得运用积分法可解得相轨迹方程为为一抛物线,其概略相轨迹如图7-5所示。
图7-5 系统的概略相轨迹(6)运用积分法可解得相轨迹方程为其中c为一常数,其相轨迹如图7-6所示。
图7-6 系统的相轨迹2.非线性控制系统结构图如图7-7所示,M =1。
要使系统产生振幅A=4,频率ω=1的自振运动,试确定参数K ,τ的值。
图7-7 系统结构图解:画出和G (jω)曲线如图8.7所示,当K 改变时,只影响自振振幅A ,不改变自振频率ω;而当τ≠0时,会使自振频率降低,幅值增加。
因此可以调节K ,τ大小实现要求的自振运动。
由自振条件N (A )G (jω)=-1即将ω=1代入上式可解得K =9.93,τ=0.322图7-8 和G (jω)曲线3.设继电型控制系统结构如图7-9所示,输入r (t )=R·1(t ),c (0)=0。