下载文档原格式
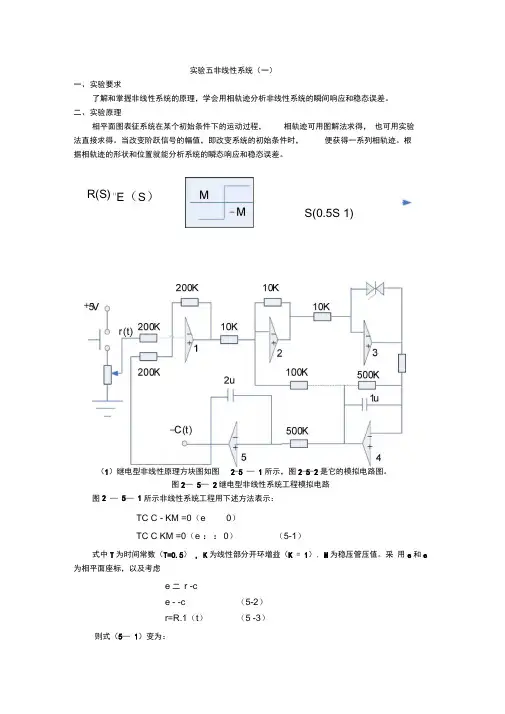
实验五非线性系统（一）一、实验要求了解和掌握非线性系统的原理，学会用相轨迹分析非线性系统的瞬间响应和稳态误差。
二、实验原理相平面图表征系统在某个初始条件下的运动过程，相轨迹可用图解法求得，也可用实验法直接求得。
当改变阶跃信号的幅值，即改变系统的初始条件时，便获得一系列相轨迹。
根据相轨迹的形状和位置就能分析系统的瞬态响应和稳态误差。
R(S) "E（S）S(0.5S 1)（1）继电型非线性原理方块图如图2-5 —1所示，图2-5-2是它的模拟电路图。
图2—5—2继电型非线性系统工程模拟电路图2 —5—1所示非线性系统工程用下述方法表示：TC C - KM =0（e 0）TC C KM =0（e ：：0）（5-1）式中T为时间常数（T=0.5）, K为线性部分开环增益（K = 1）, M为稳压管压值。
采用e和e 为相平面座标，以及考虑e 二r -ce - -c （5-2）r=R.1（t）（5 -3）则式（5—1）变为：(5-4)Te e KM = 0(e 0)Te e - KM 二 0(e ：：： 0)代入T =0.5,K =1以及所选用稳压值 M ，应用等倾线法作出当初始条件为e(0) =r(0) _c(0) =r(0) =R时的相轨迹，改变r(0)值就可以得到一簇相轨迹。
图5-1所示系统的相轨迹曲线如图 5-3所示图2 — 5- 3图2 — 5 — 1所示系统相轨迹图2 - 5 - 3中的纵坐标轴将相平面分成两个区域， (■.和I ) e 轴是两组本轨迹的分界线，系统在阶跃信号下，在区域「内，例如在初始点 A 开始相轨迹运动到分界线上的点B ,从B 点开始在趋于11内，沿区域 「内的本轨迹运动到点 C 再进入区域〔，经过几次往返运 动，若是理想继电特性，则系统逐渐收敛于原点。
(2)带速度负反馈的继电型非线性系统原理方块图如图2-5-4所示。
图2- 5- 2中的虚线用导线连接，则图 2 - 5-2就是图2 - 5-4的模拟电路。
第1篇一、实验目的1. 理解相平面的概念及其在控制系统中的应用；2. 掌握相平面分析方法，通过分析相轨迹图，了解系统的动态特性；3. 分析饱和非线性环节对控制系统性能的影响。
二、实验原理相平面分析是一种研究非线性系统动态特性的方法。
它通过将系统的状态变量绘制在二维平面上，形成相轨迹图，从而直观地观察系统的运动规律。
在相平面上，系统的状态变量可以是系统的位置和速度，也可以是系统的其他两个相互独立的变量。
本实验主要研究带有饱和非线性环节的控制系统。
饱和非线性环节具有上限和下限，当输入信号超出这个范围时，系统的输出将不再改变。
在相平面上，饱和非线性环节表现为相轨迹的折线。
三、实验设备1. PC机一台；2. MATLAB软件；3. Simulink模块库。
四、实验步骤1. 建立控制系统模型根据实验要求，建立带有饱和非线性环节的控制系统模型。
首先，建立系统的传递函数，然后添加饱和非线性环节模块。
2. 设置仿真参数设置仿真参数，包括仿真时间、采样时间等。
3. 运行仿真运行仿真，观察系统输入饱和非线性环节前后的相轨迹图。
4. 分析相轨迹图对比有无非线性环节的相轨迹图，分析饱和非线性环节对系统性能的影响。
5. 求解超调量在输入单位阶跃信号的情况下，计算系统的超调量。
五、实验结果与分析1. 相轨迹图分析在饱和非线性环节的影响下，系统的相轨迹图发生了明显的变化。
当输入信号超出饱和非线性环节的上下限时，相轨迹图出现折线。
这表明饱和非线性环节限制了系统的运动范围，影响了系统的动态性能。
2. 系统性能分析通过对比有无非线性环节的相轨迹图，可以发现饱和非线性环节对系统的超调量和上升时间有一定影响。
当饱和非线性环节存在时，系统的超调量增大，上升时间变长。
这是因为饱和非线性环节限制了系统的运动范围，导致系统在达到稳定状态之前需要更多的能量。
3. 超调量计算在输入单位阶跃信号的情况下，系统的超调量为：超调量 = (终值 - 原始值) / 原始值其中，终值为系统稳定后的输出值，原始值为输入信号的幅值。
7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。
但是，我们在介绍非线性系统的分析方法之前，先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。
因为许多非线性元件特性一般都可分段用线性方程来表示，所以非线性控制系统也可以用分段线性系统来近似。
一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。
若系统开始处于平衡状态。
试求系统在阶跃函数)(1)(0t R t r ⋅= 作用下，在e e -平面上的相轨迹。
建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e e T +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。
因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。
e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。
当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。
根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。
由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。
因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。
2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。
因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。
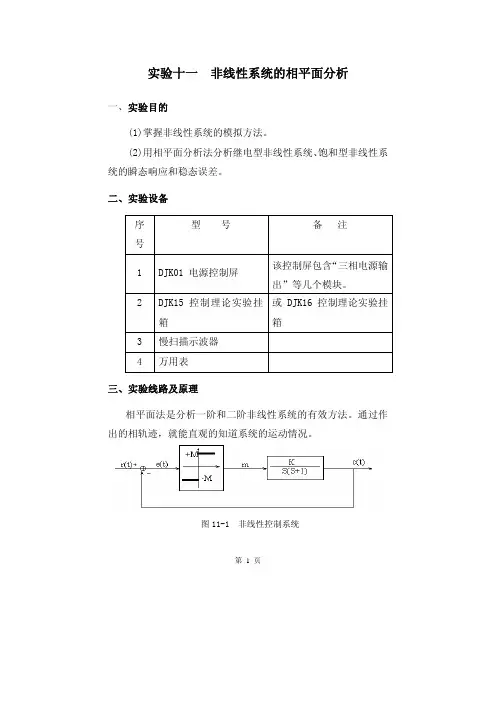
第 1 页实验十一 非线性系统的相平面分析一、实验目的(1)掌握非线性系统的模拟方法。
(2)用相平面分析法分析继电型非线性系统、饱和型非线性系统的瞬态响应和稳态误差。
二、实验设备 序号型 号备 注1DJK01 电源控制屏 该控制屏包含“三相电源输出”等几个模块。
2 DJK15控制理论实验挂箱或DJK16控制理论实验挂箱 3慢扫描示波器 4 万用表 三、实验线路及原理相平面法是分析一阶和二阶非线性系统的有效方法。
通过作出的相轨迹，就能直观的知道系统的运动情况。
图11-1 非线性控制系统第 2 页图11-2 理想继电器特性的模拟线路图图11-1为一具有理想继电器特性的非线性系统的框图，图11-2为理想继电器特性的具体接线参考图。
由图11-1得 Km C C =+。
,0,0m e m m e >⎧=⎨−<⎩则有），（），（。
0000<=++>=−+e KM C C e KM C C 令 r(t) = R，则 r(t)=0。
因为 r –c =e， 所以e= c 。
于是上式改写为），（），（。
0000<=−+>=++e KM e e e KM e e第 3 页初始条件 e（0）= r（0）- c（0）=R ，用等倾线法作出该系统的相轨迹如图11-3所示。
由图可见，系统从初始点A 出发，最后运动到坐标原点。
这不仅表明该系统稳定，而且由图还能确定系统的超调量δ%=0F/0A ×100%。
和稳定误差为零等性能指标。
图11-3四、思考题(1)实验中如何获得c 和c的信号？如何获得e 和e 的信号？ (2)试说明e ⎯e相轨迹和c ⎯c 相轨迹间的关系。
(3)你是如何从相平面图上得到超调量σρ和稳态误差ess 的？五、实验方法(1)用相轨迹分析图8-54所示的具有理想继电器特性的非线性系统在阶跃信号作用下的瞬态响应和稳态误差。
①根据图8-54设计相应的实验线路图，其中M=5V，K=1。
