实验十一：非线性系统的相平面分析

④特征根为两个正实根 对应的相轨迹以非震 荡方式从平衡点散出。这种类型的奇点称为不 稳定节点。
⑤特征根为一对共轭纯虚根，系统处于无阻尼运动状 态，系统的相轨迹是围绕平衡点的一组封闭曲线。这 种奇点称为中心点。
⑥特征根为两个符号相反的实根。此时每条相轨迹都 是先趋近平衡点，随后在尚未达到平衡点之前又 远离平衡点而去，只有4条孤立的相轨迹除外，其中 两条趋于平衡点，另两条从平衡点散出，这时奇点称 为鞍点。
②不稳定的极限环
如图(b)所示。起始于极限环内部和外部的相 轨迹，最终都卷离极限环。当系统受到很小的 扰动而偏离极限环时，系统状态再也不会回到 极限环上来，因此称为不稳定的极限环。
③半稳定的极限环 如果极限环两侧的相轨迹，一侧是卷向极限 环，而另一侧卷离极限环，则该极限环称为半 稳定的极限环，如图(c)与图(d)所示。
的位置，可以有以下几种情况：
①一对具有负实部的共轭复根 每条相轨迹都 以震荡方式无限地“卷向”平衡点，这种类型的 奇点称为稳定焦点。
②一对具有正实部的共轭复根 每条相轨迹都以 震荡方式“卷离”平衡点，这种类型的奇点称为不稳 定焦点。
③特征根为两个负 实根
对应的相轨迹以非震
荡方式趋聚于平衡点。这种类型的奇点称为稳定节点。
ai
ai
ai1 2
平均斜率依次作短直线便可画得。
说明：等倾线未必都是直线，另外，为保证精 度，等倾线分布要有适当密度，密度可不一样。
例如 x2 nxn2x0 令 0.5, n1
i.等斜线方程:
y n2 x 1 x
i.等斜线分布图.
2n a 1a
ii.相轨迹 A点
a1
1 过点A,
a
1
1 1.2 2

第2章相平面分析方法212.1相平面分析的概念2.2 线性系统的相平面分析2.3 非线性系统的相平面分析2.1 相平面分析的概念211i 2.1.1 相平面图（Phase portraits ）二阶自治系统1112(,)xf x x =&(2.1)a 2212(,)xf x x =&(2.1)b 以状态x 1与x 2为坐标的平面，称为相平面。

给定一对初值(0)=x (0)x 0，可以确定系统的一个解，在相平面中得到一条相平面轨线。

对不同初值的一簇相平面轨线称为系统的相平面图（相图）。

例2.1质量-弹簧系统k =1m=1&&系统的动态方程x x +=假设质点初始位置在x 0，其解为0()cos x t x t ==−&0()sin xt x t 相轨线方程2&22x xx +=图2.1 质量-弹簧系统相平面图相图的作用：一旦得到系统的相图，则系统对应于不同初值的特性即21展漏无遗。

从例2.1可以看出，系统的相轨线既不趋于零也不趋于无穷，而是以原点为中心的同心圆，表示系统处于临界稳定状态。

2.1.2 奇异点(Singular point)满足=奇异点是相平面上的一个平衡点。

112212(,)0(,)0f x x f x x=对线性系统，奇异点通常只有一个。

对非线性系统，则经常存在多个孤立的奇异点。

20.630x xx x +++=&&&例2.2二阶非线性系统两个奇异点：收敛区0x =3x =−奇异点是相平面不稳定奇异点的重要特征。

线性系统的稳定性完全由奇异点的本质决定，而非线性系统则会存在一些复杂22特征。

图2.2 系统相平面图2.2 线性系统的相平面分析0x axbx ++=&&&考虑下面二阶线性系统(2.2)系统的解为121212(),t tx t k e k e λλλλ=+≠111212(),ttx t k e k te λλλλ=+=系统(22)(2.2)只有一个奇异点（设b ≠0），但奇异点附近的系统轨线根据参数a 和b 的不同表现出不同的特征。

x2
0
x2
0
x1
x1
(a)稳定焦点
(b)不稳定焦点
17
图8-31 共轭复根对应的相轨迹
1, 2
a d (a d )2 4(ad bc ) 2
5）纯虚根
(a d ) 0, ad bc 0
奇点称为中心点。
x2
0
x1
图8-32
纯虚根对应的相轨迹
18
2、极限环
相平面图上的一根孤立的封闭相轨迹称为极限环。它对应系 统的自激振荡状态。极限环把相平面划分为内部平面和外部 平面两部分，相轨迹不能从环内穿越环进入环外，反之也不 能。
将（4）式代入（2）式整理得
( 4)
1
23
r r (1 r 2 ) 1
有r 0和1 r 2 0两种情况
(1) r 0
x1 0, x2 0 系统的平衡点（奇点）
b P ( x1 , x 2 ) 1 x 2 ( 0,0 )
为一常数。
根据上式可在相平面上绘制一条线，相轨迹通 过这条线上的各点时，其切线的斜率都相同， 称之为等倾线。如果取不同的值 1 , 2 ,则可 在相平面上绘制一系列的等倾线。
8
x2
1
( x10 , x20 )
2
x1
3
4
图8-27 用等倾线法绘制相轨迹
相平面中所有等倾线上的短线，组成了相轨迹的切线场。
P ( x1 , x2 ) P ( x1 , x2 ) P ( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )
Q( x1 , x2 ) Q( x1 , x2 ) Q( x1 , x2 ) x1 x2 x1 x 2 ( 0,0 ) ( 0,0 )

Ui(S )
TS
(3) 阶跃响应： Uo(t) = K + 1 t
T
(t ≥ 0)
(4) 模拟电路图：如图 1.1-6 所示。
其中 K = R1 / R0 ； T = R0C
4
自动控制原理
第 1 章 线性系统的时域分析
比例积分环节
R1
C
Ui
R0
_
10K
信号输入端
反相器
10K _
R0 = R1 = 200K; C = 1uF 或 2uF
Ui(S)
1
Uo(S)
TS
(2) 传递函数： Uo(S) = 1
Ui(S) TS
(3) 阶跃响应： Uo(t) = 1 t (t ≥ 0)
T
(4) 模拟电路图：如图 1.1-4 所示。
图 1.1-3
其中 T = R0C
Ui
R0
信号输入端
积分环节 C
_
反相器
10K
10K
_
Uo
输出测量端
R0 = 200K; C = 1uF 或 2uF
图 1.1-4 3
自动控制原理
(5) 理想与实际阶跃响应曲线对照： ① 取 R0 = 200K；C = 1uF。
理想阶跃响应曲线
Uo 无穷
Uo(t)
1 Ui(t)
0 0.2s
t
② 取 R0 = 200K；C = 2uF。
第 1 章 线性系统的时域分析
实测阶跃响应曲线
Uo
10V
Uo(t)
1 Ui(t)
(5) 理想与实际阶跃响应曲线对照： ① 取 R0 = R1 = 200K；C = 1uF。
图 1.1-6

稳定的极限环：周期运动稳定 起始于极限环内部或外部的相轨迹最终均卷向该极限环
c
0
c
三、奇点和奇线
奇线－－极限环 极限环的三种类型
不稳定的极限环：周期运动不稳定
起始于极限环内部或外部的相轨迹最终均卷离该极限
环
c
0
c
三、奇点和奇线
奇线－－极限环
极限环的三种类型
半稳定的极限环
起始于极限环内部（或外部）的相轨迹最终卷向该
三、奇点和奇线
奇点 零输入线性二阶系统奇点 (0, 0) 的分类： 焦点：当特征根为一对具有负实部的共轭复根时，奇点为
稳定焦点；当特征根为一对具有正实部的共轭复根 时，奇点为不稳定焦点。 节点：当特征根为两个负实根时，奇点为稳定节点；当特 征根为两个正实根时，奇点为不稳定节点。 鞍点：当特征根一个为正实根，一个为负实根时，奇点为 鞍点。 中心点：当特征根为一对纯虚根时，奇点为中心点。
x1 x1
0 0
x2 2
x 2
0
三、奇点和奇线
[例1]
为确定奇点类型，在奇点处将微分方程展开为泰勒级 数，并略去高次项： 在奇点 (0, 0) 处有：
f ( x, x ) 2,
x
x0 x 0
f
( x, x
x )
x0 x 0
0.5
故有：x 0.5x 2x 0
特征根： s1,2 0.25 j1.39 ，奇点为稳定焦点
a a
等倾线方程为： c(t ) c0 a(c(t ) c0 )
（相轨迹）
c
c
0
c
0
t
a0
3、线性系统的相轨迹
线性二阶系统的相轨迹 (b 0)
c
c

对于线性二阶系统的自由运动（无外作用） 对于线性二阶系统的自由运动（无外作用） ，奇点就是相平面的 原点。按系统极点的分布，奇点分为：稳定或不稳定的焦点、 原点。按系统极点的分布，奇点分为：稳定或不稳定的焦点、 稳 定或不稳定的节点、鞍点。注意中心点不是奇点。 定或不稳定的节点、鞍点。注意中心点不是奇点。 中心点不是奇点
•
x > 0 轨迹向右移
•
线性一阶系统的相轨迹
线性一阶系统自由运动的微分方程为
T x+ x = 0
相轨迹方程为： 相轨迹方程为： 设初始条件为： 设初始条件为：
•
1 x = − x T x (0) = c
•
1 x (0) = − c T
•
•
T <0
发散
•
x x
x
T >0
收敛
x
线性二阶系统的相轨迹
线性系统相平面的图解法
一．基本概念 相平面及相轨迹 相平面有关概念举例说明
二．线性系统的相轨迹 线性一阶系统的相轨迹 奇点与普通点 三.相轨迹的绘制 积分法 等倾线法 线性二阶系统的相轨迹
四.由相轨迹求时间解
非线性系统的相平面分析
本质非线性系统的线性化 非线性系统的极限环
用相平面表现运动
d2y dy +4 + 3y = 0 2 dt dt
相轨迹为向心螺旋线最终趋于原点 ( x = 0 x = 0) 。是一个收敛的运 动。对应的平衡点是稳定的焦点。
•
ζ =1时，线性二阶系统的相轨迹 时
k
存在两个相同的负实根 s1, 2 = −ζωn 相轨迹包含一根特殊的等倾线，斜率等于根，不同初始条件的相轨 相轨迹包含一根特殊的等倾线，斜率等于根， 稳定的节点。 迹最终将沿这条特殊的等倾线趋于原点。 迹最终将沿这条特殊的等倾线趋于原点。平衡点为稳定的节点。

实验九实验九 非线性系统的相平面法分析非线性系统的相平面法分析一．实验目的一．实验目的1．掌握相平面法分析非线性系统；．掌握相平面法分析非线性系统；2．用相平面法分析非线性二阶系统，并绘制相轨迹图；．用相平面法分析非线性二阶系统，并绘制相轨迹图；二．实验内容1．搭建继电型非线性二阶系统，观测并绘制其相轨迹图；．搭建继电型非线性二阶系统，观测并绘制其相轨迹图；2．搭建带速度反馈的继电型非线性二阶系统，观测并绘制其相轨迹图；．搭建带速度反馈的继电型非线性二阶系统，观测并绘制其相轨迹图； 3．搭建饱和型非线性二阶系统，观测并绘制其相轨迹图。

．搭建饱和型非线性二阶系统，观测并绘制其相轨迹图。

三．实验步骤三．实验步骤在实验中观测实验结果时，可选用普通示波器，也可选用本实验台上的虚拟示波器。

在实验中观测实验结果时，可选用普通示波器，也可选用本实验台上的虚拟示波器。

如果选用虚拟示波器，如果选用虚拟示波器，只要运行只要运行ACES 程序，程序，选择菜单列表中的相应实验项目，选择菜单列表中的相应实验项目，选择菜单列表中的相应实验项目，再选择再选择开始实验，就会打开虚拟示波器的界面，点击开始即可使用本实验台上的虚拟示波器CH1、CH2两通道观察被测波形。

具体用法参见用户手册中的示波器部分。

两通道观察被测波形。

具体用法参见用户手册中的示波器部分。

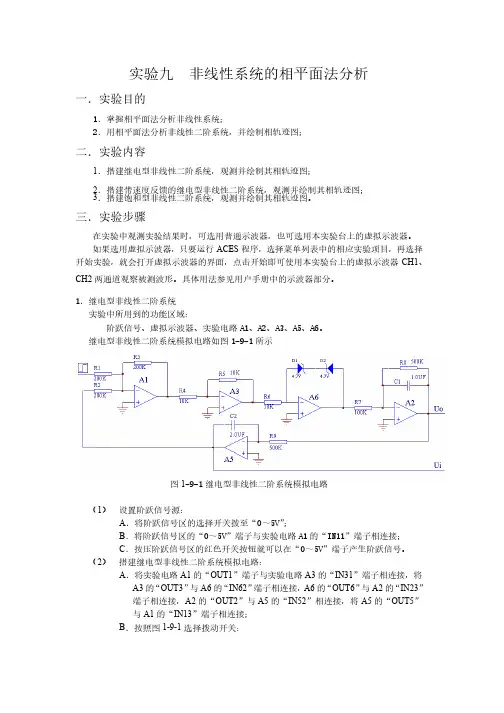
1．继电型非线性二阶系统．继电型非线性二阶系统实验中所用到的功能区域：实验中所用到的功能区域：阶跃信号、虚拟示波器、实验电路A1A1、、A2A2、、A3A3、、A5A5、、A6A6。

继电型非线性二阶系统模拟电路如图1-9-1所示所示图1-9-1继电型非线性二阶系统模拟电路继电型非线性二阶系统模拟电路（1） 设置阶跃信号源：设置阶跃信号源：A ．将阶跃信号区的选择开关拨至“．将阶跃信号区的选择开关拨至“00～5V 5V””； B ．将阶跃信号区的“．将阶跃信号区的“00～5V 5V”端子与实验电路”端子与实验电路A1的“的“IN11IN11IN11”端子相连接；”端子相连接；”端子相连接； C ．按压阶跃信号区的红色开关按钮就可以在“．按压阶跃信号区的红色开关按钮就可以在“00～5V 5V”端子产生阶跃信号。

7-5 非线性控制系统的相平面分析法相平面法在分析非线性系统时是很有用处的。

但是，我们在介绍非线性系统的分析方法之前，先讨论一下相平面法在分析线性二阶系统中的应用是很有好处的。

因为许多非线性元件特性一般都可分段用线性方程来表示，所以非线性控制系统也可以用分段线性系统来近似。

一、线性控制系统的相平面分析1、阶跃响应 设线性二阶控制系统如图7-38所示。

若系统开始处于平衡状态。

试求系统在阶跃函数)(1)(0t R t r ⋅=　作用下，在e e -平面上的相轨迹。

建立系统微分方程式，由图示系统可得Ke c cT =+ 因为c r e -=，代入上式得r r T Ke e e T +=++ （7-31） 对于->⋅=0),(1)(0t t R t r 时，0)()(==t r t r因此上式可写成0=++Ke e e T （7-32）方程（7-32）与（7-22）式相仿。

因为假设系统开始处于平衡状态，所以误差信号的初始条件是0)0(R e =和0)0(=e。

e e -平面上的相轨迹起始于)0,(0R 点，而收敛于原点(系统的奇点)。

当系统特征方程的根是共轭复数根，并且位于左半平面时，其相轨迹如图7-39(a)所示。

根据ee -平面上的相轨迹就可方便的求得c c -平面上系统输出的相轨迹，如图7-39(b)所示。

由图7-39可见，欠阻尼情况下系统的最大超调量P σ及系统在稳态时的误差为零。

因为e e -平面相轨迹最终到原点，即奇点；所以在cc -平面上相轨迹最终到达0R c =的稳态值，则奇点坐标为)0,(0R 。

2、斜坡响应 对于斜坡输入t V t r 0)(=；当0>t 时，)(t r 的导数0)(V t r= 及0)(=t r 。

因此，方程（7-31）可以写成0V Ke e eT =++ 或 0)(0=-++KV e K e e T 令v e K V e =-0，代入上式，则有0V Ke ee T =++ννν （7-33） 在v v ee -平面上，方程（7-33）给出了相平面图与在e e -平面上方程（7-32）给出的相平面图是相同的。

因此相轨迹如右图：
2.当输入信号r(t)=R+vt，则 r(t) 0, r(t) v，各区域线性 方程如下：
Te e KM v Te e Ke v Te e KM v
e0 e, x M e0 e e0 , x e e e0 , x M
可见，在线性区域，系统存在奇点位于(v/K,0)，该奇点
4. 经线性化后，非线性控制系统在各段成为了线性系 统。在相平面上，相当于将整个相平面分为若干区域， 其中每一区域对应于系统的一个线性工作状态，可由 一个线性微分方程描述，不同分区域的分界线称为相 平面开关线 。
5. 由于存在分区情况，因此系统在某个区域线性微分方 程所对应的奇点可能并不位于该区域，这类奇点称为虚 奇点，即系统实际上是无法运行到该平衡点上的。反之， 若某个区域线性微分方程对应的奇点就位于同一区域， 则称该类奇点为实奇点。
X (s) s(Ts )
将c(t)=r(t)-e(t)代入方程：
Te(t) e(t) Kx(t) Tr(t) r(t)
式中e(t),x(t)为饱和非线性的输 出。根据饱和非线性的输入输 出特性，可将相平面分为：正 饱和、负饱和以及线性区域， 如右图。
1.当输入信号r(t)=R时，r(t) 0, r(t) ，0 则各区域上线
只可能是稳定焦点或节点。在正饱和区，系统的相轨 迹渐近于该奇点只可能是稳定焦点或节点。在正饱和 区 区， ，系 系统统的的相相轨轨迹迹渐渐近近于于另α 相一线条α相e线 v ；KM在负。饱和
e v KM
根据所给的定参数的不同，这些渐近线在相平面上的 位置也不同，同时根据相轨迹走向这一性质，可画出 三种情况下系统的相轨迹如下图。
性方程如下：
二阶线性
Te e KM 0 Te e Ke 0 Te e KM 0

非线性系统的相平面分析实验指导书 合肥工业大学电气与自动化实验中心非线性系统的相平面分析实际应用中，完全线性的系统是不存在的，因为组成控制系统的元件，其静态特性都存在着不同程度的非线性，但只要系统不包含有特殊本质的非线性元件，并且传输的信号也不太大，那么根据线性系统分析法所得到的结果也同样适用于该类系统。

非线性系统与线性系统的本质区别。

线性系统输入与输出的关系可用线性微分方程来描述，能用叠加原理进行分析；而非线性系统的输入与输出的关系要用非线性微分方程描述，不能用叠加原理来分析。

线性系统的稳定性仅取决于系统本身的结构和参数，与初始条件和输入信号无关；而非线性系统的稳定性，除了与系统本身的结构和参数有关系外，还依赖于初始条件和输入信号的性质。

从频域的观点出发，给线性系统输入一个正弦或余弦信号，则输出响应也是同一频率的正弦或余弦信号，不同的仅在于输出响应的振幅和相位依系统特性和输入信号的频率而定。

输入信号振幅的变化，仅使输出响应的振幅呈比例变化，而不影响其波形，即线性系统不会输出输入信号未包含的频率分量。

但是，非线性系统输出信号的波形不仅与系统的特性有关，而且强烈地依赖输入信号的大小，即输出信号常含有输入信号所没有的频率分量。

调换线性系统各串联环节的位置不影响分析的结果；但在非线性系统中，非线性环节和线性环节的位置不能互相调换，否则会导致错误的结论。

本章实验先从典型环节的特性研究着手，然后用相平面分析法再对非线性系统的性能进行分析、研究并结合实验，描述了如何改善非线性系统的性能指标。

1.1 典型非线性环节本次实验以运算放大器为基本单元，在输入端和反馈网络中设置相应元件 (稳压管、二级管、电阻和电容) 组成各种典型非线性的模拟电路，来模拟实际系统中常见的继电、饱和、死区、间隙等典型的非线性特性，并对典型非线性特性进行详细的理论分析和实验研究，从而为非线性系统的研究打下良好的基础。

1.1.1 实验目的1．熟悉各典型非线性环节的理论分析。

ɺɺ + x + x = 0 x ɺ
ɺ x1 = x2 ɺ x2 = − x2 − x1 dx2 x2 + x1 =− =α dx1 x2 1 x2 = − x1 1+ α
等倾斜线方程
CHANG’AN UNIVERSITY
长安大学电子与控制工程学院
自动控制理论
第七章 非线性系统的分析
相轨迹的画法 α取不同值时，可在相 取不同值时， 取不同值时 平面上画出若干不同的 等倾线， 等倾线，在每条等倾线 上画出表示该等倾线斜 率值的小线段， 率值的小线段，这些小 线段表示相轨迹通过等 倾线时的方向， 倾线时的方向，从相轨 迹的起点按顺序将各小 线段连接起来， 线段连接起来，就得到 了所求的相轨迹 。
tAB = tB − tA = ∫
x
.
xA
0 o
x
D
.
x 3 x 2 x 1θ A
θB θ CD θ BC
x
θ AB
x
θ
p
B
A
C
CHANG’AN UNIVERSITY
长安大学电子与控制工程学院
自动控制理论
第七章 非线性系统的分析
x = x1 p cosθ + ox1 ɺ x = x1 p sin θ
长安大学电子与控制工程学院
自动控制理论
第七章 非线性系统的分析
二、由相轨迹求暂态响应 点移动到X 【问题的提出】：相轨迹上坐标 XA点移动到 B点 问题的提出】 所需的时间。 所需的时间。 解决方法之一】 【解决方法之一】
dx1 x2 = ɺ x2 = x1 dt xB dx 1 tB − tA = ∫ xA x 2
x x 【解】 mɺɺ + kx = ɺɺ + x = 0

实验五 非线性系统的相平面分析法一、实验目的1. 进一步熟悉非线性系统的电路模拟研究方法；2. 熟悉用相平面法分析非线性系统的特性。

二、实验设备同实验一。

三、实验内容1. 用相平面法分析继电型非线性系统的阶跃响应和稳态误差；2. 用相平面法分析带速度负反馈的继电型非线性控制系统的阶跃响应和稳态误差；3. 用相平面法分析饱和型非线性控制系统的阶跃响应和稳态误差。

四、实验原理非线性系统的相平面分析法是状态空间分析法在二维空间特殊情况下的应用。

它是一种不用求解方程，而用图解法给出x 1=e ，x 2=e的相平面图。

由相平面图就能清晰地知道系统的动态性能和稳态精度。

本实验主要研究具有继电型和饱和型非线性特性系统的相轨迹及其所描述相应系统的动、静态性能。

1. 未加速度反馈的继电器型非线性闭环系统 图5-1为继电器型非线性系统的方框图。

图5-1 继电型非线性系统方框图由图5-1得0=-+KM c cT (0>e ) 0=++KM c cT (0<e ) 式中T 为时间常数(T=0.5)，K 为线性部分开环增益，M 为继电器特性的限幅值。

因为 c r e -=)(1t R r ⋅= c e-= 则有0=++KM e eT (0>e ) (5-1) 0=-+KM e eT (0<e ) (5-2) 基于 de e d e e = ， 令 dee d =α 则式(5-1)改写为KM e e -=+ α5.0 α5.01+-=KMe (5-3)同理式(5-2)改写为KM e e=+ α5.0 α5.01+=KMe (5-4)根据式(5-3)、(5-4)，用等倾线法可画出该系统的相轨迹，如图5-2所示。

不难看出，该系统的阶跃响应为一衰减振荡的曲线，其稳态误差为零，其中A 线段表示超调量的大小。

图5-2 阶跃信号作用下继电器型非线性系统的相轨迹2. 带有速度负反馈的继电型非线性闭环控制系统 图5-3为带速度负反馈的继电型非线性系统的方框图。

一、实验目的1. 了解非线性系统在自动控制中的应用及其特点。

2. 掌握非线性系统相平面分析方法，分析非线性系统动态性能。

3. 通过实验验证非线性环节对系统性能的影响。

二、实验原理非线性系统是指系统输出与输入之间存在非线性关系的系统。

非线性系统的特点是动态性能复杂，难以用线性理论进行分析。

相平面分析是研究非线性系统动态性能的一种有效方法。

本实验采用相平面分析方法，分析带有饱和非线性环节的控制系统动态性能。

饱和非线性环节是一种常见的非线性环节，其特点是输入输出之间存在饱和限制。

三、实验设备1. PC机一台2. MATLAB软件3. Simulink仿真工具箱四、实验步骤1. 建立带有饱和非线性环节的控制系统模型。

2. 设置系统参数，包括饱和非线性环节的上限和下限。

3. 对系统进行仿真，记录系统输入饱和非线性环节前后的相轨迹图。

4. 分析相轨迹图，比较有无非线性环节的性能。

5. 求解超调量。

五、实验结果与分析1. 建立控制系统模型本实验控制系统模型为：\[ G(s) = \frac{K}{1 + Ts} \]其中，K为比例增益，T为时间常数。

饱和非线性环节为：\[ f(x) = \begin{cases}0 & \text{if } x \leq -0.5 \\x & \text{if } -0.5 < x < 0.5 \\1 & \text{if } x \geq 0.5\end{cases} \]2. 设置系统参数设K=1，T=0.1，饱和非线性环节上限和下限分别为0.5和-0.5。

3. 仿真结果（此处插入仿真结果相轨迹图）从相轨迹图可以看出，饱和非线性环节对系统性能有显著影响。

在饱和非线性环节存在的情况下，系统相轨迹出现弯曲，动态性能变差。

4. 性能分析（1）超调量超调量是衡量系统响应速度和稳定性的重要指标。

本实验中，饱和非线性环节导致系统超调量增加，说明系统响应速度变慢，稳定性变差。

0
M
x h2 h2 x h1
x h1
(7 4a)
.
当x 0:
M
y
0
M
x h1 h1 x h2
x h2
(7 4b)
19
图（b）所示继电特性的数学描述由 读者自行导出。
20
4、间隙特性
传动机构的间隙也是控制系统中常见的非线性 特性，齿轮传动是典型的间隙特性，图7-4（a） 表示齿轮传动原理，图7-4（b）表示主动轮位移 与从动轮位移的关系。设主动轮与从动轮间的最 大间隙为2b，那么当主动轮改变方向时，主动轮 最大要运动2b从动轮才能跟随运动。间隙特性类 似于线性系统的滞后环节，但不完全等价，它对 控制系统的动态、稳态特性都不利。设齿轮传动 速比为，则图7-4间隙特性的数学描述为：
22相平面法是庞加莱poincare1885年首先提出的本来它是一种求解二元一阶非线性微分方程组的图解法两个变量构成的直角坐标系称为相平面方程组的解在相平面上的图象称为相轨这里是将相平面法用于分析一阶尤其是二阶非线性控制系统并形成了一种特定的相平面法它对弄清非线性系统的稳定性稳定域等基本属性解释极限环等特殊现象起到了直观形象的作23因为绘制两维以上的相轨迹是十分困难的所以相平面法对于二阶以上的系统几乎无能为力
一点在 x x平面上绘出的曲线，表征了系统的
运动过程，这个曲线就是相轨迹。我们用一个二 阶线性时不变系统来体验一下相平面和相轨迹。
26
例7-1 考虑二阶系统：
..
x ax 0 , a 0, x(t0 ) x0 ,
将它写成微分方程组：
dx
.
x
dt.
d x ax
dt
两式相除得到：
.
dx dx

非线性系统的相平面分析实验一典型非线性环节一.实验要求1. 了解和掌握典型非线性环节的原理。

2. 用相平面法观察和分析典型非线性环节的输出特性。

二.实验原理及说明实验以运算放大器为基本元件, 在输入端和反馈网络中设置相应元件 (稳压管、二极管、电阻和电容组成各种典型非线性的模拟电路,模拟电路见图 3-4-5 ~ 图 3-4-8所示。

1.继电特性理想继电特性的特点是:当输入信号大于 0时,输出 U 0=+M,输入信号小于 0,输出 U 0=-M。

理想继电特性如图 3-4-1所示, 模拟电路见图 3-4-5, 图 3-4-1中 M 值等于双向稳压管的稳压值。

图 3-4-1 理想继电特性图 3-4-2 理想饱和特性注:由于流过双向稳压管的电流太小(4mA ,因此实际 M 值只有 3.7V 。

实验步骤:(1 将信号发生器 (B1 的幅度控制电位器中心 Y 测孔, 作为系统的 -5V~+5V输入信号 (Ui : B1单元中的电位器左边 K3开关拨上(-5V ,右边 K4开关也拨上(+5V 。

(2模拟电路产生的继电特性:继电特性模拟电路见图 3-4-5。

图 3-4-5 继电特性模拟电路①构造模拟电路:按图 3-4-5安置短路套及测孔联线,表如下。

(b 测孔联线②观察模拟电路产生的继电特性:观察时要用虚拟示波器中的 X-Y 选项慢慢调节输入电压(即调节信号发生器 B1单元的电位器,调节范围 -5V~+5V ,观测并记录示波器上的 U 0~Ui 图形,如下图:由图得 M=3.77V(3函数发生器产生的继电特性①函数发生器的波形选择为‘继电’ ,调节“设定电位器1” ,使数码管右显示继电限幅值为 3.7V 。

②测孔联线:③观察函数发生器产生的继电特性:观察时要用虚拟示波器中的 X-Y 选项慢慢调节输入电压(即调节信号发生器 B1单元的电位器,调节范围 -5V~+5V ,观测并记录示波器上的 U 0~Ui 图形。

相平面和相轨迹
相平面：
由系统变量及其导数（如 c,）c
构成的用以描述系统状态的平面。
相轨迹：
系统变量及其导数随时间变化 在相平面上描绘出来的轨迹。
例1 单位反馈系统
G(s) 5 s(s 1)
n 2.236 0.2236
r(t) 1(t)
相平面法的基本概念
相轨迹的性质：相轨迹的斜率
任一个二阶 微分方程可
dx& 5 dx 3
x
dx& x& x 0
dx
x& 0
相轨迹的性质：相轨迹的奇点
x 0, x& 0
x&
只有奇点，不能够
确定斜率，这个时
x
候有多条相轨迹交
与此点
再谈奇点
➢非线性系统可能有多个奇点
dx& f (x, x&) 0
dx
x& 0
&x& 0.5x& 2x x2 0
dx& 0.5x& 2x x2 0
dx
x&
0
x 0 x 2 x& 0 x& 0
➢奇点特性可以用其附近的小信号分析
相轨迹的性质：相轨迹正交于x轴
dx& x& x x
dx
x& 0
dx& dx
x&
x
相轨迹的性质：相轨迹运动的方向
随着时间推移，
x& 0 x增加，相轨迹
向右边移动
随着时间推移，
x& 0 x减少，相轨迹
向左边移动
x& x
x
0
对于线性定常系统，原点是惟一的平衡点。

实验二非线性系统分析2．1典型非线性环节2.1.1 实验目的1．掌握各典型非线性环节模拟电路的构成方法，掌握TDN-AC/ACS设备的使用方法。

2．了解参数变化对典型非线性环节动态特性的影响。

2.1.2 实验要求1．观察各种典型非线性环节的动态特性曲线2．观测参数变化对典型非线性环节动态特性曲线的影响2.1.3 实验设备1．TDN-AC/ACS 系列教学实验系统一套。

2．慢扫描示波器一台。

3．PC机一台。

4．连接导线。

2.1.4 实验原理本实验以运算放大器为基本元件，在输入端和反馈网络中设置相应元件（稳压管，二极管，电阻和电容）组成各种典型非线性环节的模拟电路。

1．继电特性：见图2 . 1－1图2.1－1 继电特性模拟电路理想继电特性如图2 . 1－2所示。

图中M值等于双向稳压管的稳压值。

U0UiM-M图2.1－2 理想继电特性 （2）饱和特性：见图2.1－3及图2 . 1－4图2.1－3 饱和特性模拟电路 图2.1－4理想饱和特性在理想饱和特性图2.1－4中，特性饱和值等于稳压管的稳压值，斜率K 等于前一级反馈电阻值与输入电阻值之比，即:1/R R K f (3)死区特性死区特性模拟电路图:见图2.1－5Ui+－+－R0U010K10KRfIN R2R1AB30K +12V -12V30K OUTU9 NC图2.1－5 死区特性模拟电路死区特性如图2.1－6所示。

KU0UiK图2.1－6 死区特性 图2.1－6中特性的斜率K 为： 0R R K f =死区)(4.0)(123022V R V R =⨯=∆ 式中2R 的单位为K Ω，）＝（12R R 。

（实际Δ还应考虑二极管的压降） （4）间隙特性间隙特性的模拟电路图见图2.1－7。

间隙特性如图2.1－8所示，图中间隙特性的宽度Δ为)(4.0)(123022V R V R =⨯=∆ 式中2R 的单位为K Ω，）＝（12R R 。

特性斜率αtg 为： 0R R C C tg ff i ⋅=α 改变2R 和1R 可改变间隙特性的宽度；改变R R f 或）（ttC C 的比值可调节特性斜率）（αtg 。