水动力弥散系数

水动力弥散方程解析解的适用条件和优缺点尽管解析解法在求解复杂的水动力弥散方程定解中存在一定缺陷，但仍然不它的作用可以忽略。

室内或现场试验应根据解析解的实际情况进行设计，并应使用解析解拟合观测数据，以获得水动力弥散系数。

在解析解中，瞬时注入点源问题的解称为基本解。

从基本解出发，利用叠加原理导出了线源、面源、多点源和连续注入的解。

因此，点源问题的求解是所有解的基础，需要引起高度重视。

（1）空间瞬时点源的求解其基本条件是：①均质各向同性介质；②静止流场u?0，弥散系数为常数，流体密度为常数（ρ=常数）；③t?0时，在原点处瞬时注入溶质的质量为m。

以瞬时点源的位置为原点，可以得出浓度c是相对于原点对称的。

可简化出纯弥散方程：C2c？2c？2c？d（2？2？2）？T十、Y式中，D表示多孔介质的分子扩散系数。

从这个公式可以看出，它是球对称的，这有利于纯色散模式的应用和讨论。

取半径为r和r+dr的两个球面所构成的单元体为均衡段，根据质量均衡有：WNjdr？WNjdr？博士vv？CTc、 VV是平均值吗？式中，W为球面面积；N为有效孔隙度；JD是色散通量，JD？？D平衡截面的空隙体积。

忽略高阶微量，化简后得：c1？？CD2.（r2）？TR所以点源的定解问题可以写成：cd2cr(rr0,t>0)tr2rrc(r,t)t00(r>0)c（r，t）r0（t>0）0c(r,t)r?0?0(t>0)CN4.r2dr？m（t>0）（该式将点源处浓度限制在有限区域）通过玻尔兹曼变换，将原偏微分方程的定解问题转化为常微分方程的定解问题，得到空间瞬时点源的解如下：c(r,t)?m8n(?dt)32e?r24dt① 浓度可以从球面上的原点获得；② 任何时间的最大浓度都在原点处，原点处的浓度随时间的增加而降低。

（2）空间瞬时无限线源解空间瞬时无限线源的作用可看着点源的连续分布，因考虑到点源基本解的微分方程是线性的，故采用叠加的方法，即积分法，可得空间无限线源的基本解为：c（r，t）？m1e4？无损检测？r24dt从上式可看出，浓度c与z无关，即在z方向不产生弥散问题。

土壤水动力弥散系数的室内测定土壤水动力弥散系数是土壤力学领域里的一项重要参数，它用来描述土壤的水动力特性。

它被广泛地应用在土壤水动力特性研究中，也很重要的用来决定土壤水分的运移和分布方式以及污染物在土壤中的迁移规律等。

它的测定对于研究土壤水动力特性及其在土壤水分运移和分布方式以及污染物迁移影响等方面有着重要意义。

土壤水动力弥散系数的测定一般采用室内试验法。

在实验前，首先要将待测试的土壤按照一定的测定标准筛选，同时要进行现场取样，并根据土壤的分布特性，选择有代表性的土壤样本，注意土壤样本的稳定性，以防止试验结果受到土壤水动力弥散系数的瞬时变化影响。

室内土壤水动力弥散系数测定实验需要使用水动力室，这个水动力室由负压箱、滤过柱、测定管、活性炭柱、电极、流量计等组成，用来进行土壤水动力的测定。

在实验中，首先要将土壤样本装入负压箱中，然后以一定的水流量，在负压箱中向土壤样本喷入一定的水，在滤过柱和活性炭柱的作用下，土壤中的有机物及无机盐离子等杂质过滤掉，最后通过电极测定流入及流出的水的电导率和温度，并根据电势差为土壤水动力弥散系数求得最终结果。

此外，室内测定法在测定土壤水动力弥散系数时还要考虑室内试验参数和环境条件对土壤水动力弥散系数的影响。

一般来说，当系统处于室内环境时，室内温度、湿度、空气压强等会影响土壤水动力弥散系数的测定结果，因此在使用室内测定法时，要求温度、湿度、空气压力都保持在一定的范围内，以保证测定结果的准确性。

以上就是对室内测定土壤水动力弥散系数的基本原理和过程的介绍，室内测定法用来测定土壤水动力弥散系数非常实用，但由于空气压强等室内环境条件的影响，要求操作者掌握足够的实验技能，以保证测定结果的准确性，同时也要进行大量的实验研究，以保证实验结果的准确性和有效性。

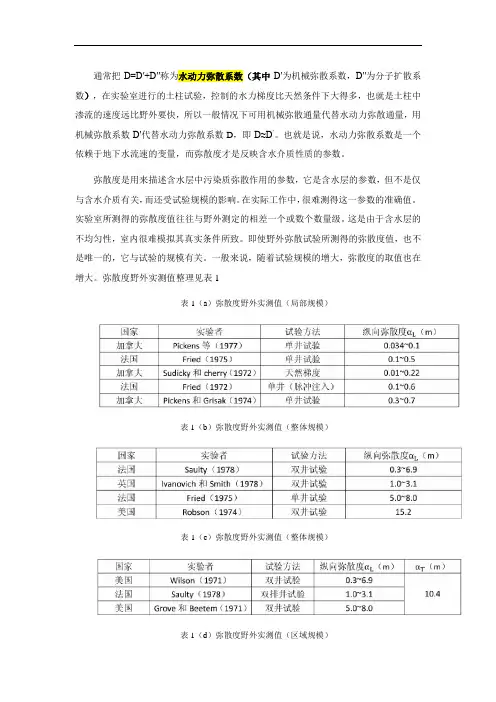
通常把D=D′+D″称为水动力弥散系数（其中D′为机械弥散系数，D″为分子扩散系数），在实验室进行的土柱试验，控制的水力梯度比天然条件下大得多，也就是土柱中渗流的速度远比野外要快，所以一般情况下可用机械弥散通量代替水动力弥散通量，用机械弥散系数D′代替水动力弥散系数D，即D≈D’。

也就是说，水动力弥散系数是一个依赖于地下水流速的变量，而弥散度才是反映含水介质性质的参数。

弥散度是用来描述含水层中污染质弥散作用的参数，它是含水层的参数，但不是仅与含水介质有关，而还受试验规模的影响。

在实际工作中，很难测得这一参数的准确值。

实验室所测得的弥散度值往往与野外测定的相差一个或数个数量级。

这是由于含水层的不均匀性，室内很难模拟其真实条件所致。

即使野外弥散试验所测得的弥散度值，也不是唯一的，它与试验的规模有关。

一般来说，随着试验规模的增大，弥散度的取值也在增大。

弥散度野外实测值整理见表1
表1（a）弥散度野外实测值（局部规模）
表1（b）弥散度野外实测值（整体规模）
表1（c）弥散度野外实测值（整体规模）
表1（d）弥散度野外实测值（区域规模）
据孙讷正著《地下水污染数——数学模型和数值方法》（1989），纵向弥散系数D L是纵向弥散度αL与空隙平均流速V m的乘积，即：D L=αL·V m。

水动力弥散系数一、基本概念在研究地下水溶质运移问题中，水动力弥散系数是一个很重要的参数。

水动力弥散系数是表征在一定流速下，多孔介质对某种污染物质弥散能力的参数，它在宏观上反映了多孔介质中地下水流动过程和空隙结构特征对溶质运移过程的影响。

水动力弥散系数是一个与流速及多孔介质有关的张量，即使几何上均质，且有均匀的水力传导系数的多孔介质，就弥散而论，仍然是有方向性的，即使在各向同性介质中，沿水流方向的纵向弥散和与水流方向垂直的横向弥散不同。

一般地说，水动力弥散系数包括机械弥散系数与分子扩散系数。

当地下水流速较大以致于可以忽略分子扩散系数，同时假设弥散系数与孔隙平均流速呈线性关系，这样可先求出弥散系数再除以孔隙平均流速便可获取弥散度。

分子扩散系数D '与介质的性质有关。

经验证明：T D D d ⋅=' (6-25)式中 d D ——溶质在静水中的分子扩散系数，它主要取决于溶质分子的特性和温度；T ——多孔介质的弯曲度。

机械弥散系数D ''是一个与地下水流速有关的量。

在各向同性介质中，经试验证明为：UU U U D ji T L ij T ij )(ααδα-+='' (6-26)式中 ij δ——Kronecker 记号，当j i =时，1=δ，当j i ≠时，0=δ；L α——纵向弥散度； T α——横向弥散度；U ——地下水实际速度，i U 、j U 为实际速度的分量；二、水动力弥散系数确定的试验方法水动力弥散系数可通过室内或现场弥散试验确定。

弥散系数的计算方法一般分两类：一是利用解析公式直接或间接求解；二是采用标准曲线对比法。

1.一维室内弥散试验测定水动力弥散系数 （1）试验原理以人工配制的均质各向异性岩样，进行示踪剂注入实验。

具体假设及要求如下： ①. 试验流场为均质不可压缩的稳定的一维流场，渗流为定水头补给的一维弥散； ②. 多孔介质是均质的，渗透系数，孔隙度和弥散系数都是常数； ③. 流体是不可压缩的均质液体，密度、粘滞度为常数，温度不变； ④. 试验土柱（或砂柱）及其中之流体，示踪剂的初始浓度为一定值。

弥散地质学术语弥散又称水动力弥散或水力弥散，为溶质示踪物稀释时的扩散现象。

当一定数量溶质示踪物在地下水流中运移而逐渐传播时，可以占据超出地下水平均流速所影响的范围，愈扩愈大。

弥散是由质点的热动能和流体的对流而引起的，是分子扩散和机械混合两种作用的结果。

所以弥散具有分子扩散和机械弥散两种作用。

在渗透性能较好的含水层中，地下水流速较大时，机械弥散作用比分子扩散作用大，有时可忽略后者；而在较细颗粒的多孔介质中，地下水流速通常很慢，分子扩散作用比较明显。

释义地下水流中的溶质(如污染物、示踪剂等)沿流向逐渐传播扩散，并在渗流区域中占有愈来愈大的体积的现象。

主要由两类基本现象组成。

一为对流，亦称“机械弥散”。

指污染物随水流一起在岩石或土的孔隙中流动，不断被分散进入更多的孔隙，因而在岩石或土中占据愈来愈多的体积。

二是分子扩散，由含污染物的水和不含污染物的水中的溶质浓度差引起。

即使在静水中也能产生分子扩散。

沿地下水流向的弥散称“纵向弥散”，垂直于地下水流向的弥散称“横向弥散”。

在地下水污染预测、地下水人工回灌和海岸带的咸水入侵的研究中有重要的应用。

分子扩散静止水体中的溶质在溶液浓度梯度的作用下，从浓度高处向浓度低处的运移现象。

分子扩散与分子、离子及质点的热运动有关，最终可使溶液浓度达到平衡。

溶液中溶质的分子扩散速度服从费克(Fick)定律。

机械弥散恒温条件下多孔介质中流体所产生的溶质扩散效应。

在总体上，水流应按某一平均流速运动。

但由于孔隙、裂隙分布的不均匀，几何形状和大小的不同，实际上溶质示踪物是沿着曲折的渗透途径运动的，水流的局部速度在大小和方向上发生着变化，引起溶质在介质中扩散的范围愈来愈大。

弥散系数弥散系数表征地下水中溶质迁移的重要水文地质参数，它表征在一定流速下，多孔介质对某种溶解物质弥散能力的参数。

水动力弥散系数是一个与流速及多孔介质有关的张量。

具有方向性，即使在各向同性介质中，沿水流方向的纵向弥散系数和垂直水流方向的横向弥散系数也不相同，但天然条件下，大多数地下水垂向上的水流运动很小，弥散作用可忽略。

壤水动力弥散系数的室内测定Experimental Determination of Coefficient of SoleHydrodynamic DispersionZHAI Chun-shene SHAO Ai-jun Peng Jian-ping ZhangYong-qiang2(1.Qingdao Geologic and Mineral geotechnicalengineering Co. ，Ltd ，Qingdao 26607 China ；2.Shijiazhuang University of EconomicsShijiazhuang05003 China)：Hydrodynamic dispersion experiment was done with unsaturated silt loam.Depend on mass conservation lawthe formulas to calculate coefficient of hydrodynamic dispersion was developed.According to the data of soilwater and salt regime measured from the upright soilcolumn，the coefficient of hydrodynamic dispersion was calculated ，and the relation between hydrodynamicdispersion and average flow velocity in soil voids was，and built up.This approach has clear concept of physics the formulas are simple and applied.Keywords：Coefficient of hydrodynamic dispersionSolute flux ；Unsaturated soil东 ､ 胡毓骐， 1992)[1] 。

土壤水动力弥散系数研究
土壤水动力弥散系数是指土壤中水的运动能力，它是土壤水分运动的重要参数，也是土壤水分运动模拟的重要参数。

土壤水动力弥散系数的大小取决于土壤的结构、粒径、孔隙度、孔隙水分压力、孔隙水分流动等因素。

土壤水动力弥散系数的研究对于提高土壤水分运动模拟的准确性具有重要意义。

目前，研究者们采用多种方法来研究土壤水动力弥散系数，如实验室实验、地面观测、模拟模型等。

实验室实验是研究土壤水动力弥散系数的最常用方法，它可以模拟土壤水分运动的实际情况，并可以获得准确的结果。

地面观测是研究土壤水动力弥散系数的另一种方法，它可以直接观测土壤水分运动的实际情况，从而获得准确的结果。

模拟模型是研究土壤水动力弥散系数的另一种方法，它可以根据土壤水分运动的实际情况，建立模型，从而获得准确的结果。

综上所述，土壤水动力弥散系数的研究对于提高土壤水分运动模拟的准确性具
有重要意义，目前研究者们采用实验室实验、地面观测和模拟模型等多种方法来研究土壤水动力弥散系数，以获得准确的结果。