层次分析法在商洛市旅游景点选择中的应用

层次分析法在旅游综合决策中的应用摘要：层次分析法是一种定性与定量分析相结合的多目标决策分析方法，将决策者的经验判断给予量化，对目标(因素)结构复杂而且缺乏必要的数据情况下，采用此方法较为实用，是常用的一种系统分析方法。

本文通过一个旅游问题的实例来说明其在分析决策中的应用，这种分析的方法可以推而广之，解决其他决策问题，是决策应用的通行思路。

关键词：层次分析法旅游决策一：背景在日常生活中，我们会遇到许多决策问题。

例如选择旅游景点，选择升学志愿，选择职业，选择科研课题等等。

人们在决策时，要考虑涉及到经济、社会、人文等方方面面的因素：选择旅游景点经常会考虑景色、费用和居住、饮食、交通等条件是否舒适和方便；要选择升学志愿，必然要考虑到你本人的兴趣爱好、学习基础、专业前途以及收费标准等因素；选择职业一般依据工作环境、工资待遇、发展前途、住房条件等因素；选择科研课题一般依据课题的可行性、应用价值、理论价值、被培养人才等因素。

当我们面临各种各样的方案，在对这些因素作比较、判断、评价、决策时，常常无法量化这些因素的重要性、影响力或者优先程度，人的主观选择会起到作用，因此，应用常规的数学方法解决这一问题带来本质上的困难。

美国运筹学家托马斯·沙旦(T.L.Saaty)等人在20 世纪70 年代提出了一种能有效处理这类问题的实用方法，即层次分析法（Analytic Hierarchy Process，AHP）。

层次分析法这是一种定性和定量相结合的、系统化的、层次化的分析方法。

过去研究自然和社会现象主要有机理分析法和统计分析法两种方法，前者用经典的数学工具分析现象的因果关系，后者以随机数学为工具，通过大量的观察数据寻求统计规律。

近年发展的系统分析是又一种方法，而层次分析法是系统分析的数学工具之一，它把一个复杂问题分解成组成因素，并按支配关系形成层次结构，然后应用两两比较的方法确定决策方案的相对重要性。

由于层次分析法在处理复杂的决策问题上的实用性和有效性，目前，层次分析法在经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗、环境保护、冲突求解及决策预报等领域得到了广泛的应用。

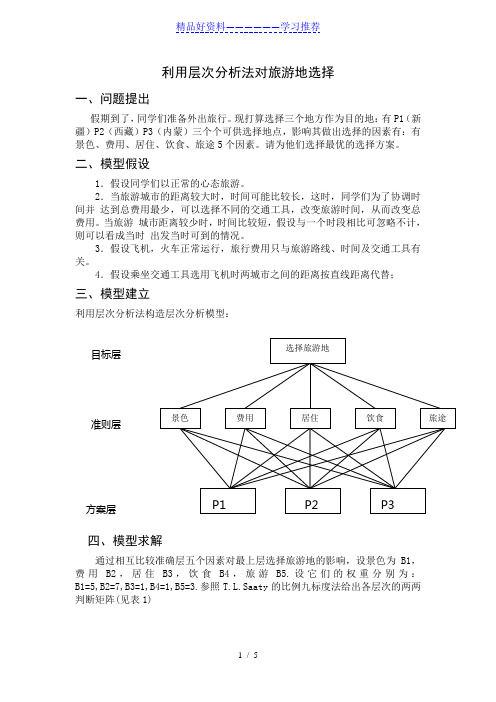
利用层次分析法对旅游地选择一、问题提出假期到了，同学们准备外出旅行。

现打算选择三个地方作为目的地：有P1（新疆）P2（西藏）P3（内蒙）三个个可供选择地点，影响其做出选择的因素有：有景色、费用、居住、饮食、旅途5个因素。

请为他们选择最优的选择方案。

二、模型假设1．假设同学们以正常的心态旅游。

2．当旅游城市的距离较大时，时间可能比较长，这时，同学们为了协调时间并达到总费用最少，可以选择不同的交通工具，改变旅游时间，从而改变总费用。

当旅游城市距离较少时，时间比较短，假设与一个时段相比可忽略不计，则可以看成当时出发当时可到的情况。

3．假设飞机，火车正常运行，旅行费用只与旅游路线、时间及交通工具有关。

4．假设乘坐交通工具选用飞机时两城市之间的距离按直线距离代替；三、模型建立利用层次分析法构造层次分析模型：四、模型求解通过相互比较准确层五个因素对最上层选择旅游地的影响，设景色为B1，费用B2，居住B3，饮食B4，旅游B5.设它们的权重分别为：B1=5,B2=7,B3=1,B4=1,B5=3.参照T.L.Saaty的比例九标度法给出各层次的两两判断矩阵(见表1)表1 同学们对准则层各因素相对重要性的两两比较判断矩阵B1 B2 B3 B4 B5 权重系数B1 1 5/7 5/3 3 5/3 0.364B2 7/5 1 7/1 7/1 7/3 0.374B3 1/5 1/7 1 1 1/3 0.183B4 1/5 1/7 1 1 1/3 0.481B5 3/5 3/7 3 3 1 0.237 λ=0.3006 CI=0.003 CR=0.001同学们对给出方案层的判断矩阵相同，都是如下结果（见表2，表3，表4）表2 同学们就提出的三个方案在景色上面的两两判断矩阵P1 P2 P3 权重系数P1 1 1 1/2 0.237P2 3 1 3/2 0.362P3 2 2/3 1 0.311 λ=0.3012 CI=0.004 CR=0.010表3就同学们提出的三个方案在费用上的两两判断矩阵P1 P2 P3 权重系数P1 1 2/3 2 0.492P2 3/2 1 3 0.124P3 1/2 2/3 1 0.271 λ=3.0007 CI=0.003 CR= 0.005 表4同学们就提出的三个方案在住宿方面的两两判断矩P1 P2 P3 权重系数P1 1 2/3 2 0.643P2 3/2 1 3 0.124P3 1/2 2/3 1 0.431 λ=3.013 CI=0.0065 CR=0.011P1 P2 P3 权重系数P1 1 1/2 2 0.265P2 2 1 5 0.606P3 1/2 1/5 1 0.129 = 3.023 CI=0.004 CR=0.007P1 P2 P3 权重系数P1 1 4 6 0.691P2 1/4 1 2 0.204P3 1/6 1/2 1 0.105 =3.013 CI=0.0065 CR=0.011五、模型分析层次单排序及一致性检验 根据层次分析法的计算步骤，必须对以上的六个表的两两判断矩阵进行层次单排序，计算各自的权重系数，并对它们逐个进行一致性检验。

基于层次分析法的旅游景点选择应用层次分析法（AHP）是一种多准则决策方法，可以帮助旅游者选择最适合他们的旅游景点。

该方法可以帮助旅游者根据他们的偏好和需要对不同的景点进行比较和评估，以便做出最佳的选择。

下面我们将介绍如何使用AHP来选择旅游景点。

1.确定标准首先，旅游者需要确定选择旅游景点的标准。

例如，您希望景点具有美丽的风景、历史文化遗产和娱乐设施等等。

您应该根据您的优先级制定一个清晰的标准列表，以便稍后进行比较。

2.创建层次结构接下来，您需要创建一个包含标准和景点的层次结构。

这个层次结构应该先从最高级别开始，然后逐步细化到次级别。

例如：第一层：选择标准第二层：美丽的风景、历史文化遗产、娱乐设施第三层：旅游景点1、旅游景点2、旅游景点33.建立判断矩阵判断矩阵是用来比较标准和景点之间的重要性的。

您需要为每个标准和景点创建一个权重，这个权重是一个百分比，表示该标准或景点在您的选择中的重要性。

例如：您认为美丽的风景比历史文化遗产和娱乐设施更重要，应该赋予它更高的权重。

美丽的风景：0.5历史文化遗产：0.3娱乐设施：0.24.计算一致性比率在AHP中，一致性是一个很重要的概念，因为它可以帮助您检查您的权重是否合理。

为了计算一致性比率，您需要对比每个标准和景点的一对判断，然后计算它们的一致性指数。

接下来，您需要把这些指数加起来，得出一个总体一致性指数CAL。

例如，如果您认为美丽的风景比历史文化遗产更重要，则比较这两个标准的一致性指数如下：美丽的风景比历史文化遗产更重要：1历史文化遗产比美丽的风景更重要：3然后您必须计算这两个一致性指数的比率，以了解它们之间的一致性。

如果这个比率超过0.1，则意味着您的权重是不一致的。

您需要重新调整它们的权重，直到比率小于0.1。

5.计算最终权重一旦您确定了每个标准和景点的权重，并检查了它们之间的一致性，您就可以计算出每个景点的最终权重。

计算公式为：最终权重=标准权重×景点权重。

基于多因素模糊综合评价的商洛旅游景点线路分析屈正庚;卢琼【摘要】以陕西省商洛旅游业为例,选取了8个3A级以上的旅游景点作为研究对象,进行旅游景点线路和价值分析.建立了景点模型及景点逻辑网络图,首先采用Kruskal算法和Dijkstra算法对这8个旅游景点进行最短旅游线路分析;其次建立了景点价值模型,采取多因素模糊综合评价法研究这8个旅游景点的旅游价值,数字化的方式计算每个景点的旅游价值;最后对景点价值结果进行分析,从追求旅游期望值最高、追求最短旅游线路与节约时间、平衡旅游期望值最高和线路最优3个方面设计最佳旅游线路.从不同角度满足旅游者的实际需求,对进一步提高商洛旅游业发展水平和打造精品旅游路线有实际意义.%Taking Shangluo tourism in Shaanxi Province as an example,8 well-known tourist attractions above 3A level were selected as the research object,and the route and value of tourist attractions were analyzed.We established the model of scenic spots and the logical network of scenic spots,and used Kruskal algorithm and Dijkstra algorithm to analyze the shortest tourist routes of the eight scenic spots.Then we established the scenic spot value model and adopted the multi-factor fuzzy comprehensive evaluation method to study the tourism of the eight tourist attractions value and calculate the tourism value of each attraction by the digitized way.Finally,the author analyzed the value of the attraction and designed the best tourism from the following three aspects:pursuing the highest tourism expectation,pursuing the shortest tourist route and saving time,balancing the highest tourism expectation and the best route line from different angles to meet the actual needs oftourists,to further enhance the tourism development in Shangluo andbuild quality tourism routes for help.【期刊名称】《河南科学》【年(卷),期】2018(036)001【总页数】5页(P136-140)【关键词】模糊综合评价法;最优路线;最短路径;商洛旅游景点【作者】屈正庚;卢琼【作者单位】商洛学院数学与计算机应用学院,陕西商洛 726000;商洛学院数学与计算机应用学院,陕西商洛 726000【正文语种】中文【中图分类】TP301.6当今世界旅游业蓬勃发展，遍地开花，旅游市场空间日趋扩大，旅游景点在旅游业中的地位和作用日益凸显.我国近几年大力发展旅游业，提出“绿色、生态、环保”的口号，不断建设美丽乡村、特色小镇等旅游项目.旅游一方面可以把人的注意力从日常繁忙的工作和生活琐事中转移开，满怀快乐的心情感受大自然的美丽，旅游另一方面可以陶冶人的情操、提高道德修养、开阔视野.近几年，我国的旅游事业已受到越来越多的关注，显示出了强大的生命力和巨大的发展潜力，并逐渐成为我国经济发展的生力军.2016年我国旅游景点接待游客超过了44亿人次，旅游收入达到4.96万亿元人民币，取得了良好的经济效益、社会效益和生态效益.据测算2017年能达到50亿人次，具有广阔的前景.陕西省在第十二次党代会上明确指出了旅游业的发展是西部强省建设的主要途径之一，因此，陕西省政府发挥自然资源、地理位置优势，努力打造绿色品牌，紧紧围绕“关中为圆圈，陕南陕北为两个翅膀”目标方针，全面挖掘“秦岭最佳生态旅游地”，让经济、文化、旅游水平快速提高.商洛作为陕南城市，融入西安一小时经济圈，紧邻秦岭山脉，具有独特的生态资源优势.目前，商洛市政府全面打造“秦岭最美是商洛”的品牌，积极推动文化发展与生态旅游深度融合［1］.因此，本文以商洛旅游景点为研究对象，深入分析商洛各个旅游景点旅游线路发展现状和存在问题，采用多因素模糊综合评价法设计和规划各个旅游景点线路，目的是提高现代人生活质量，发挥商洛旅游资源优势，提升商洛经济水平，优化商洛旅游线路，增强商洛旅游品牌效应［2］.1 多因素模糊综合评价法概述模糊综合评价法是根据模糊数学中隶属度理论原理，把一种定性评价转化为定量评价的方法，在处理问题方面逻辑紧密、结构清晰、系统完整，适合各种非定型问题的求解.模糊综合评价法是对多种属性的对象受到多种因素制约而做出一种合理判断的综合方法，通过精确的数字化方式处理模糊的问题，能够做出科学、合理的评价结果，以评价值为1作为基准进行最优的评价，具体处理问题时需要构建和确定模糊综合评价指标及合成评价矩阵和权重值［3-4］.2 商洛旅游景点模型的建立与分析2.1 商洛旅游景点概述商洛位于陕西东南部，秦岭山脉腹地，总面积19 292 km2，下设商州区、洛南县、丹凤县、山阳县、商南县、镇安县、柞水县，即一区六县.商洛市位于商州区境内.商洛生态资源丰富、自然环境优美、高速公路密集、名胜古迹众多、历史人文丰厚，具有发展自然生态旅游业的得天独厚条件，本文针对商洛一区六县旅游景点进行研究.近年来，商洛市委、市政府把生态旅游业作为全市的主导产业来抓，已建成国家级自然保护区1个、省级自然保护区4个、国家级森林公园4个、省级森林公园5个、国家5A级旅游景区1个、4A级旅游景区4个、省级风景名胜区2个，形成了丹江文化旅游线路，商州—山阳、商洛—丹凤—洛南绿色体验旅游线路，镇安、柞水原生态休闲度假旅游线路等精品线路.目前，商南金丝峡已创建为国家5A级旅游景区和国家级地质公园，柞水牛背梁、山阳天竺山、镇安木王森林公园、柞水溶洞已创建为国家4A级旅游景区和国家级地质公园，丹凤丹江漂流、山阳月亮洞、洛南老君山已创建为国家3A级旅游景区.2016年商洛接待游客数量达到3734万人，实现旅游综合收入199亿元.实践证明，大力发展生态文化旅游产业符合商洛实际、符合科学发展观要求，必须深入挖掘“秦岭最美是商洛”品牌，做大做强生态文化旅游产业，优化旅游精品线路. 2.2 商洛旅游景点模型的建立以陕西省商洛旅游景点作为研究对象，选取了3A及以上8个比较有名的旅游景点进行研究，如图1所示.再对这8个旅游景点进一步逻辑抽象，抽象出具体的逻辑网络图（图2）［5-6］.2.2.1 克鲁斯卡尔（Kruskal）算法Kruskal算法就是把所有的边按照权值由小到大排序，再按照一定顺序选取每条边，如果这条边的两个端点不在同一集合，那么将其合并，直到所有端点存放在同一个集合为止.对逻辑网络图2采取Kruskal算法进行最短路径优化，得到图3［7-8］.图1 商洛旅游景点相对位置图Fig.1 Shangluo tourist attractions map但在实际中，旅游者从原点出发需要回到原点，我们通过回路的方式进一步优化线路（图4）.2.2.2 迪杰斯特拉（Dijkstra）算法Dijkstra算法是一种典型的单路最短路径算法，用于寻找一个端点到其他所有端点的最短路径，任意选择某一端点作为起点，以起点为中心向外扩展，直到扩展到所有端点为止.对图2采取Dijkstra算法求解最短路径，其结果与Kruskal算法所求的结果相同，即如图3所示.在实际中，旅游者外出旅游最终需要回归到原处，因此，采取Dijkstra算法求出最短回路路径，其结果仍然与Kruskal算法求出的回路路径结果一样，即如图4所示［9-10］.图2 商洛旅游景点逻辑网络图Fig.2 Shangluo tourist attractions logical network注：图2中0表示商洛市，1～8序号分别代表8个旅游景点，各个序号之间的数字代表景点与景点及景点与商洛市之间的距离，单位是km.图3、图4相同.图3 Kruskal算法最短路径图Fig.3 Kruskal algorithm shortest path图4 Kruskal算法回路路径图Fig.4 Kruskal algorithm loop path2.3 商洛旅游景点模型结果分析以商洛一区六县的8个3A级以上旅游景点作为研究对象，深入分析与设计这8个旅游景点线路.首先勾画出了这8个旅游景点相对位置图；其次对8个旅游景点相对位置图进一步抽象分析与数字描述，形成了景点网络逻辑图；再次选取两种非常经典的最短路径求解算法计算这8个旅游景点的最短路径.结果表明，这两种算法求解出的最短路径图是一样的.按照实际生活中的常理，外出旅游线路一般需要形成一个回路，需要对最短路径图进行回路优化设计，结果发现这两种算法得到的回路路径图仍然是一样的.总之，采用这两种经典算法设计和优化商洛8个旅游景点路线图是可靠的、可行的、有价值的，也符合实际需求，建立的商洛旅游景点模型具有实际意义.3 商洛旅游景点价值模型的建立与分析3.1 商洛旅游景点价值模型建立对商洛旅游景点进行现场考察、问卷调查与调研，再结合实际情况，综合考虑旅游景点的各自特色，全面衡量旅游景点的价值，给出如下模型：评价集V=｛很值，值得，不值｝；因素集R=｛服务质量，基础设施，门票价格｝，对8个景点进行模糊集权重值分配，如表1所示［11-12］.根据表1的数据，针对金丝峡景点构造模糊矩阵为：则对此景点的模糊综合评价为：表1 景点模糊集权重值Tab.1 Attractions fuzzy set weights价值模型因素商洛旅游景点序号3 2 4 5 6 7 8 V很值值得不值服务质量R 基础设施门票价格1 0.70 0.20 0.10 0.60 0.20 0.20 0.50 0.30 0.20 0.30 0.35 0.35 0.65 0.20 0.15 0.500.30 0.20 0.40 0.40 0.20 0.30 0.40 0.30 0.70 0.25 0.05 0.55 0.30 0.15 0.500.30 0.20 0.40 0.30 0.30 0.55 0.30 0.15 0.40 0.40 0.20 0.40 0.40 0.20 0.500.25 0.25 0.50 0.30 0.20 0.50 0.25 0.25 0.60 0.20 0.20 0.20 0.40 0.40 0.400.40 0.20 0.30 0.30 0.40 0.55 0.35 0.10 0.60 0.20 0.20 0.45 0.30 0.25 0.300.30 0.40 0.20 0.40 0.40 0.70 0.10 0.20 0.15 0.40 0.45 0.30 0.35 0.35 0.300.40 0.30 0.50 0.25 0.25评价结果表明，55%的人推荐很值得去金丝峡，23%的人推荐值得去，22%的人推荐不值得去［13-14］，同时也说明不同旅游者欣赏旅游景点的角度也是不一样的.因此，在金丝峡模糊综合评价集的结果基础上，再利用多因素综合评价法的评价矩阵和权重值的合成方法计算金丝峡景点的最终综合旅游价值.一般在此方法中，计算某个景点的综合旅游价值，需要对评价集的结果乘上一个系数，通常选取奇数值或者偶数值，本文选取5、3、1作为计算系数值.利用5、3、1系数值进一步对评价集进行量化，得到的每个评价集综合评价结果用变量Y来表示，最终求出金丝峡景点综合旅游期望值：Y1=0.55×5+0.23×3+0.22×1=3.66，即金丝峡景点的综合旅游期望值为3.66.采用相同的方法对其他7个景点进行旅游价值计算，使用相同的评价合成系数计算其他7个景点的最终综合旅游期望值如表2所示.表2 景点旅游推荐率和期望值Tab.2 Tourist attractions recommended rates and expectations景点序号景点序号1 2 3 4值得旅游的推荐率/A 0.55 0.45 0.53 0.41 0.23 0.33 0.30 0.38 0.22 0.22 0.22 0.21期望值/Y 3.66 3.46 3.77 3.40 5 6 7 8值得旅游的推荐率/A 0.47 0.46 0.37 0.39 0.27 0.3 0.28 0.32 0.26 0.24 0.35 0.29期望值/Y 3.42 3.44 3.04 3.203.2 商洛旅游景点价值模型结果分析选取商洛8个旅游景点进行分析与计算，现将表2中期望值结果放大100倍按照从大到小顺序排序，得到表3结果.表3 景点旅游价值Tab.3 Tourist attractions景点序号期望值3 1 2 6 5 4 8 7 377366346344344340320304由于这8个景点旅游者在一天时间内无法游完，需要设计最佳旅游线路，表1、表3的结果作为设计旅游线路的参考［15-16］.1）追求旅游期望值最高，满足旅游者需求的线路.假设旅游者从商洛市区出发，最终回到市区，追求旅游价值最大化的目标出发［17］，则旅游线路为：3→1→2→6→5→4→8→7.2）按照Dijkstra算法，追求最短路径旅游线路，满足旅游者节约时间的需求.同样假设旅游者从商洛市区出发，最终回到市区［18］，则旅游线路为：5→2→4→6→4→7→8→1.3）综合考虑各种因素，平衡旅游期望值最高和线路最优，满足旅游者放松心情、减轻压力的需求.同样假设旅游者从商洛市区出发，最终回到市区［19-20］，则旅游线路为：5→2→3→6→4→8→1→7.4 结语采用多因素模糊综合评价法对商洛8个旅游景点进行研究，目的是提高商洛旅游业发展、优化商洛精品旅游线路打造、提升商洛经济文化水平.针对本文的研究结果，给出几点建议.①景点的服务质量有很大上升的空间，需要有关部门加强景点各个方面的服务水平，提高导游、管理人员文化素质和服务意识.②景点的基础设施有待进一步完善，比如，景点的服务大厅、游客休闲场所、停车场、景点游览线路等需要加强.③景点的门票价格需要进一步权衡，通过旅游者游览景点以后给出的评价，可以得出景点的旅游价值与门票价格存在一定的偏差.④需要进一步全方位优化和包装商洛旅游景点，取长补短，发展地方特色旅游.综上所述，商洛处在陕西秦岭山脉以南，整体经济状况、交通便利程度、生活水平与省会城市相比，还存在一定差距，需要今后努力完善与提升.【相关文献】［1］黄明旺，郑明贵.基于ANP-灰色模糊评价法的矿业项目投资风险评价研究［J］.江西理工大学学报，2015，36（4）：37-40.［2］何荣军，卢艳，王钧.基于AHP模糊评价法在草菇蛋卷研制中的应用［J］.浙江工业大学学报，2015，43（1）：73-77.［3］李鹏，彭舜磊，张文杰.三门峡市大气环境质量模糊数学综合评价［J］.河南科学，2016，34（9）：1414-1419.［4］侯乐，杨辉华，樊永显.基于ILS-CS优化算法的个性化旅游线路研究［J］.计算机科学与探索，2016，10（1）：142-150.［5］张子寒，张落成.基于多种模型的旅游线路规划探讨［J］.计算机应用，2016，36（1）：278-280.［6］屈正庚.层次分析法在旅游评价体系中的研究［J］.计算机技术与发展，2016，26（7）：169-173.［7］张笑白，秦志学.高峰期内旅游路线实时优化调度仿真研究［J］.计算机仿真，2017，34（5）：243-246.［8］李慧曼，苏依拉，王斐.基于约束与CHNN的旅游线路问题研究［J］.内蒙古工业大学学报，2016，35（1）：5-11.［9］李航飞，高维忠.基于空间计量分析的广东省旅游业发展水平区域差异探究［J］.信阳师范学院学报（自然科学版），2016，29（1）：71-75.［10］张颖.基于AHP-模糊综合评价法的生态旅游集聚区游客满意度研究［J］.安徽农业科学，2015，43（23）：202-206.［11］陈青松，马耀峰，李森.基于模糊物元法的我国六大城市旅游供给评价研究［J］.河南科学，2014，32（11）：2366-2372.［12］屈正庚，王重英.层次分析法在旅游业中的应用研究［J］.系统仿真技术，2014，10（4）：286-290.［13］王丽.洛阳市入境旅游客源市场亲景度研究［J］.信阳师范学院学报（自然科学版），2015，28（3）：350-354.［14］屈正庚.层次分析法在商洛市农家乐评价体系中的研究［J］.计算机系统应用，2016，25（9）：236-240.［15］郭奇青，李伟.基于灰熵决策模型的景区旅游线路规划算法［J］.计算机工程与设计，2017，38（7）：1988-1991.［16］肖春景，夏克文，乔永卫.基于动态聚类的旅游线路推荐［J］.计算机应用，2017，37（8）：2395-2400.［17］张广海，孟禺.基于AHP的乡村旅游资源评价［J］.曲阜师范大学学报，2017，43（2）：84-89.［18］赵洪阳，薛伟.基于模糊综合评价法的兴安落叶松人工林采伐迹地火险等级评价［J］.西部林业科学，2016，45（4）：60-65.［19］刘洪波，李玲君，蒋博龄.模糊综合评价法在工业园区末端水处理技术评估中的应用［J］.环境污染与防治，2017，39（6）：644-649.［20］曹威威，姜小纳，王恒.旅游气候资源价值的模糊综合评价［J］.河南科学，2015，33（6）：1032-1039.。

基于层次分析法的旅游景点选择应用在旅游出行中，选择合适的旅游景点是至关重要的。

然而，很多时候旅游者会困惑于众多景点之间的选择。

为了帮助旅游者更好地选择旅游景点，我们可以利用层次分析法进行决策分析。

层次分析法是一种经典的多准则决策方法，被广泛应用于各种决策分析问题中。

它的核心思想是将决策问题分解为多个层次，将复杂的决策问题简化成易于理解的层次结构，然后通过对各层次之间的比较来确定最终的决策结果。

在旅游景点的选择问题中，我们可以将决策问题分解为三个层次：目标层、准则层和方案层。

在目标层，我们需要确定自己旅游的目标，比如休闲度假、文化探险、自然风光观赏等等。

在准则层，我们需要确定影响景点选择的各种因素，比如交通便利性、景点知名度、景点口碑等等。

在方案层，我们需要列出各种旅游景点方案。

接下来，我们需要对每个层次进行权重分析，以确定各个准则和方案的重要程度。

可以采用问卷调查、专家咨询等多种方法进行权重分析。

例如，在准则层中，我们可以邀请一些旅游专家或者常常旅游的人士，询问他们对各种准则的看法和评价，并根据他们的意见，确定各个准则的相对重要程度。

在确定了各个层次的权重之后，我们可以利用层次分析法的计算方法，对各个方案进行比较。

具体来说，我们可以采用层次分析法的征求意见矩阵法，将各个方案与准则的比较结果输入到一个矩阵中，通过计算矩阵的特征向量来确定最终权重，进而确定最优的旅游方案。

在结果评价方面，我们可以利用一些数据分析方法，比如聚类分析、主成分分析等等，对各个方案的优劣进行评价和比较。

此外，我们还可以采用一些可视化工具，比如地图、图表等等，为旅游者提供更直观、易懂的决策支持。

总之，基于层次分析法的旅游景点选择应用，可以帮助旅游者更加科学、合理地选择旅游景点，提高旅游的质量和效果。

虽然该方法需要一定的专业知识和数据分析技能，但只要认真学习掌握，就可轻松应对各种旅游决策问题。

基于层次分析法的旅游景点选择应用本文从网络收集而来，上传到平台为了帮到更多的人，如果您需要使用本文档，请点击下载按钮下载本文档（有偿下载），另外祝您生活愉快，工作顺利，万事如意！1.概念层次分析法是对一些较为繁琐问题作出决策的简易方法，它尤其适用于那些不易完全定量分析的问题，是一种层次化的、定性和定量相结合的分析方法。

近年发展起来的系统分析是一种新方法，而层次分析法是其数学工具之一。

它是美国运筹学家教授于上世纪70年代初期提出的一种简便而又实用的多准则决策方法。

2.层次分析法的原理与步骤建立层次结构模型。

应用层次分析法处理决策问题时，首先要把问题层次化，构造出一个有层次的结构模型。

在模型中，复杂问题被分解为因素的组成部分。

这些因素又按其属性及关系形成几个层次。

上一层次的因素对下一层次有关因素起支配作用。

这些层次可分为三类：最高层：这一层次中通常只有一个因素，一般它是分析问题的设定目标或最终结果，因此也称为目标层。

中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。

最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

在层次分类及因素选取时，我们要注意三点：1）上层对下层有支配作用；2）同一层因素不存在支配关系；3）每层因素一般不要超过9个。

构造成对比较阵。

面对的决策问题：要比较n个因素x1、x2…xn对目标z的影响。

我们要确定它们在C中所占的比重，即这n个因素对目标C的相对重要性。

我们用两两比较的方法将各因素的重要性量化。

每次取两个因素xi和xj，用正数aij表示与aij=SX1aijSX），aij>0，i，j=1，…，n的重要性之比。

全部比较结果得到的矩阵A=n*n称为成对比较阵。

显然有如何选取aij呢？萨迪提出了一种方法：用数字1，2，…，9及其倒数1/2，1/3，…，1/9作为标度，其意义是在每两个级别之间有一个中间状态，可分别取值2，4，…，8。