量 第十九章 4(薛定谔方程 一维方势阱 隧道效应 线性谐振子)2009
- 格式:ppt
- 大小:1.81 MB
- 文档页数:57






一维无限深势阱薛定谔方程求解一维无限深势阱是量子力学中最经典的问题之一,其求解对于理解基本的量子力学原理以及波函数的性质具有重要的意义。
薛定谔方程是描述量子力学体系中粒子的行为的基本方程,通过求解薛定谔方程,我们可以获得系统的波函数及其相应的能级。
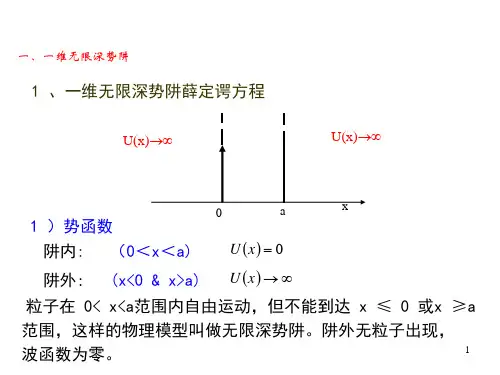
让我们来考虑一个无限深势阱,这个系统可以简单地用一个势能函数来描述。
在这个系统中,粒子只能在一个有限的空间区域内运动,而且势能在这个区域内是常数为零的。
首先,我们需要写出薛定谔方程。
对于一维情况,薛定谔方程可以写成:-ħ²/2m * d²ψ(x)/dx²+ V(x)ψ(x) = Eψ(x)。
其中,ψ(x)是系统的波函数,V(x)是势能函数,E是波函数对应的能量。
对于无限深势阱,势能函数在阱内为零,在阱外为无穷大。
因此,V(x)在阱外的值可以视为一个很大的正数。
接下来,我们需要考虑边界条件。
在无限深势阱中,粒子是被约束在一个有限空间内的。
因此,在边界处,粒子的波函数必须为零。
对于一个无限深势阱,边界条件可以写为ψ(0)=ψ(a)=0,其中,a是阱的宽度。
现在,让我们尝试求解薛定谔方程。
由于系统的势能在阱内为零,薛定谔方程可以简化为:-d²ψ(x)/dx² = k²ψ(x),其中,k=√(2mE/ħ²)。
这是一个常微分方程,我们可以通过分离变量和积分来求解。
假设ψ(x)可以分解为两个函数的乘积:ψ(x) = X(x)Y(y)。
将这个假设代入方程中,并整理得:1/X(x) * d²X(x)/dx² = -1/Y(y) * dY(y)/dy = -k²。
我们可以分别对X(x)和Y(y)进行求解,然后将两个解再组合起来得到系统的波函数。
针对常微分方程1/X(x) * d²X(x)/dx² = -k²,我们可以得到其解为X(x) = Asin(kx) + Bcos(kx),其中,A和B是常数。



一维无限深方势阱中势阱中粒子的能级公式推导一维无限深方势阱是量子力学教学中常见的模型之一。
在这个模型中,粒子被限制在一个长度为L的势阱中运动,势阱的势能在阱内为零,而在阱外则无限大。
研究一维无限深方势阱中粒子的能级公式推导,可以帮助我们更深入地理解量子力学中的基本概念和数学工具。
下面我将按照深度和广度的要求,从简单的物理概念和数学原理开始,逐步推导一维无限深方势阱中粒子的能级公式,并带有个人的观点和理解。
一、基本概念和数学工具1.1 势阱势阱是一种常见的量子力学模型,它可以用来描述粒子在受限空间中的运动。
在一维无限深方势阱中,势能在阱内为零,而在阱外为无限大,这意味着粒子在阱内具有确定的能量,而在阱外无法存在。
1.2 薛定谔方程薛定谔方程是描述量子力学中粒子运动的基本方程。
对于一维无限深方势阱而言,薛定谔方程可以简化为一维定态薛定谔方程:\[ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} = E\psi(x) \]其中,ψ(x)是粒子的波函数,m是粒子的质量,E是粒子的能量,ħ是普朗克常数。
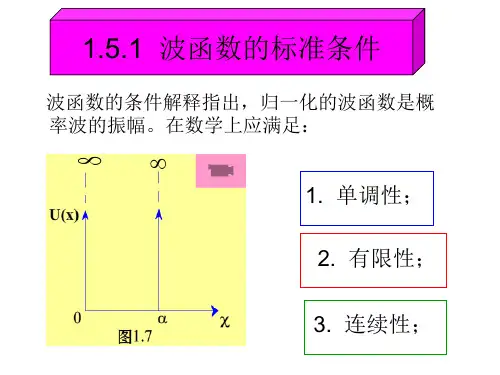
二、能级公式的推导2.1 边界条件在一维无限深方势阱中,粒子受到势阱两侧的限制,因此波函数在势阱边界处为零。
这意味着在x=0和x=L处,波函数满足边界条件:\[ \psi(0) = 0 \]\[ \psi(L) = 0 \]2.2 波函数的解根据边界条件,我们可以求解一维定态薛定谔方程得到波函数的解。
波函数的解具有以下形式:\[ \psi_n(x) = \sqrt{\frac{2}{L}}\sin(\frac{n\pi x}{L}) \]其中,n为能级量子数。
2.3 能级公式将波函数的解代入一维定态薛定谔方程中,可以得到粒子的能级公式:\[ E_n = \frac{n^2\pi^2\hbar^2}{2mL^2} \]其中,En为粒子的能量,n为能级量子数。
三、个人观点和理解在推导一维无限深方势阱中粒子的能级公式过程中,我们利用了量子力学基本的数学工具和物理概念,如薛定谔方程、波函数和边界条件。