大学物理-一维定态薛定谔方程的应用
- 格式:pdf
- 大小:2.01 MB
- 文档页数:24



第一章+薛定谔方程,一维定态问题
第一章+薛定谔方程,一维定态问题
本章主要介绍量子力学的基础概念和薛定谔方程的推导及其在
一维定态问题中的应用。
量子力学是描述微观世界中物质及其运动规律的理论。
在量子力学中,粒子的运动状态由波函数描述,波函数可以用来计算粒子在不同位置的概率密度。
薛定谔方程是量子力学中最基本的方程之一,它描述了波函数随时间的演化规律。
一维定态问题是指一个粒子在一维空间中的运动状态是定态的,即粒子的波函数只包含一个能量本征态。
在一维定态问题中,薛定谔方程可以简化为一维薛定谔方程,可以通过求解该方程得到粒子的能量本征态和能量本征值。
本章将详细介绍薛定谔方程的推导过程和一维定态问题的求解
方法,包括定态薛定谔方程的解法和粒子在势阱和势垒中的运动规律。
同时还将介绍相关的数学工具和物理概念,如波函数、能量本征态、能量本征值和概率密度等。
通过学习本章内容,读者将能够了解量子力学的基本概念和薛定谔方程的应用,掌握一维定态问题的求解方法,为后续学习量子力学的进阶内容奠定基础。
- 1 -。

第一章薛定谔方程,一维定态问题
薛定谔方程是描述量子力学中微观粒子运动的基本方程,也是研究原子、分子、固体等微观粒子体系行为的重要工具。
在一维定态问题中,我们假设粒子在一个长度为L的有限区域内运动,边界处满足一定的边界条件。
这种假设简化了问题的复杂性,使得我们能够更加深入地研究粒子在有限区域内的定态行为。
一维定态问题的薛定谔方程可以写成如下的形式:
$$-
\frac{\hbar^{2}}{2m}\frac{d^{2}\Psi(x)}{dx^{2}}+V(x)\Psi(x)=E \Psi(x)$$
其中,$\hbar$为约化普朗克常数,m为粒子的质量,V(x)为粒子在x位置处的势能,E为粒子的总能量,$\Psi(x)$为描述粒子波函数的解析函数。
一维定态问题中,由于波函数只与一个坐标x有关,因此我们可以采用分离变量的方法将波函数表示为如下形式:
$$\Psi(x)=\psi(x)e^{ikx}$$
其中,$\psi(x)$为关于x的解析函数,k为波矢。
将上式代入薛定谔方程,可将其简化为如下形式:
$$-\frac{\hbar^{2}}{2m}\psi''(x)+(V(x)-E)\psi(x)=0$$
这个简化后的方程可以通过求解得到波函数的解析表达式及对应的能量。
对于有限区域内的粒子,我们需要根据边界条件来限定波函数的形状,在定态问题中,我们通常采用周期性边界条件或硬壳边界条件。
通过分析一维定态问题的波函数和能谱,我们可以深入理解原子、分子、固体等复杂体系中微观粒子的行为规律,同时也可以为设计新的材料、光电子器件等提供理论基础和指导。
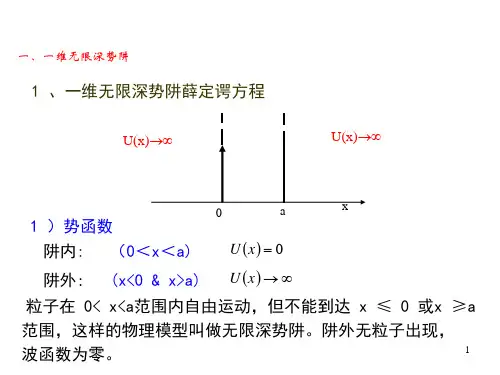
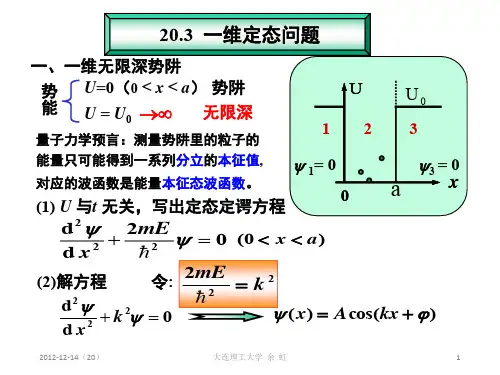





一维定态薛定谔方程的应用授课人:物理科学与技术学院势 阱日常生活中的各种井(阱)物理学中研究微观粒子运动状态时常用的模型,因其势能函数曲线的形状如同井而得名水井窨井陷阱UxOaU()U x xOa∞∞00()0 , x aU x x x a≤≤⎧=⎨∞<>⎩这是一个理想化的物理模型, 应用定态薛定谔方程求解波函数, 有利于进一步理解在微观系统中 能量量子化和概率密度等概念这样的势能函数称为 一维无限深势阱建立定态薛定谔方程并求解 假设微观粒子质量为 ,由 m 222d()()()2d U x x E x m x ψψ⎡⎤-+=⎢⎥⎣⎦x a U x 0()0≤≤=阱内( ) : 222d ()()2d x E x m xψψ-=x x a U x 0 , ()<>→∞阱外( ): 令: 222mE k =得通解: ()sin()x A kx ψϕ=+ 微观粒子的能量不可能达到无穷大,所以粒子不可能在阱外出现,或者说粒子在阱外出现的概率为零。
()0x ψ≡222d 0d k xψψ+=利用标准条件确定 和 k ϕ因 在整个 轴上必须连续 x ()x ψsin() 0()0 0 0A kx x ax x x ϕψ+≤≤⎧=⎨<>⎩,(0)sin 0A ψϕ== a A ka ()sin()0ψϕ=+=求归一化的波函数 一维无限深势阱中 微观粒子的波函数2220π()d sin d a n x x A x xa ψ+∞-∞=⎰⎰221A a =⋅= 2A a= n a x x a x ax x aπ2sin0()00 , ψ⎧≤≤⎪=⎨⎪<>⎩()π()sin 1,2,3n x A x n aψ==⋅⋅, 0ϕ=πn k a=()1,2,3n =⋅⋅⋅,微观粒子在势阱中的能量只能取一系列不连续的分立值,即能量是量子化的。
整数称为量子数 确定能量的可能取值n 由及 222mE k =πk an =得 ()2221,2,3,8n hma n E n ==⋅⋅⋅ 1n =时, 称基态能量 2128h E ma =2228n h n E ma=O4n =3n =2n =1n =基态2228n h n E ma=O4n =3n =2n =1n =基态能级间隔: ()212Δ218n n n h E E E n ma +=-=+2Δ1n E α∝表明: 当 时(宏观尺度), a →∞Δ0n E →能级消失、能量连续分布,回归经典情况。
当时 ,相对能级间隔 n →∞2Δ210n n E n E n+=→同样可视为连续分布,回归经典概率密度的分布 由归一化的定态波函数2πsin 0()0 0 ,n x x a x a ax x aψ⎧≤≤⎪=⎨⎪<>⎩概率密度函数22πsin0=0 0 , n x x a a a x x a⎧≤≤⎪⎨⎪<>⎩2()()n n p x x ψ=波函数()x ψ概率密度2()()p x x ψ=xψO xOψxOψa xOpxOpxOpa 2a 2aU x Oa 0U 0(0)()0(0,)U x a U x x x a ≤≤⎧=⎨<>⎩该势能函数称作一维矩形势垒假设能量为 的粒子从左侧射来 E 按经典观点,若 ,粒子可以 0E U >通过,若 ,粒子不能通过。
0E U < 按量子力学观点,无论 或0E U >粒子都有可能通过。
0E U <EⅠ Ⅱ Ⅲ若质量为的粒子在某力场中运动时,其势能函数为mUxOaU EⅠ Ⅱ Ⅲ0 , 0x x a U <>=当时,222d ()()2d x E x m x-= ψψ令 2122mEk =()02222m U E k -=令 2202d ()()2d U x E x m x ψψ⎡⎤-+=⎢⎥⎣⎦0 x a <<当时,0()U x U E=>222d ()()()2d U x x E x m x ψψ⎡⎤-+=⎢⎥⎣⎦由一维定态薛定谔方程可得2212d ()()0d x k x x += ψψ(0 , )x x a <>求解可得波函数的通解为( 0 )x a <<2222d ()()0d x k x x= -ψψ112211i i 1122i i 33e e ( 0 )()e e (0)e e( )k x k xk x k xk x k xA B x x A B x a A B x a ψ---⎧+<⎪=+<<⎨⎪+>⎩含时的一维定态波函数 i(,)()eEtx t x ψψ-= U xOaU EⅠ Ⅱ Ⅲ沿 x 轴正向传播的波 沿 x 轴负向传播的波,因Ⅲ区无反向波,故30B =U xOaU 11221i i 1122i 3e e ( 0 )()e e (0)e ( )k x k x k x k xk x A B x x A B x a A x a ψ--⎧+<⎪=+<<⎨⎪>⎩i(,)()eEtx t x ψψ-= 人们将微观粒子能够穿透比其总能量更高的势垒的现象形象地称为隧道效应。
由于 ,这说明当粒子的总能量时,粒子仍然有一定的概率穿透垒到达III 区。
30A ≠0E U <就好像在势垒中挖 了一些隧道,微观粒子可以从隧道中穿过势垒波函数的通解为()0002161exp 2E E a m U E U U ⎛⎫⎛⎫≈--- ⎪ ⎪⎝⎭⎝⎭数值计算表明: 对 、 和 的变化非常敏感, T a 0()U E -m 而且随着 、 、和 的增大,按指数规律迅速减小。
a 0U m 透射系数 : 透射波的强度 与入射波的强度 之比T 23A 21A 2321T AA=对于能量 不大 的低速粒子 E 粒子粒子能量势垒高度势垒宽度透射系数 电子 1eV 2eV 0.510.024质子1eV2eV10210m -⨯10510m-⨯10210m -⨯38310-⨯隧道效应只发生在微观领域,是微观粒子具有波动性的体现。
在宏观领域观察不到。
微观粒子的隧道效应已被许多实验所证实。
1981年,德国的宾尼希和瑞士 的罗雷尔利用电子的隧道效应,发明了扫描隧道显微镜,简称STM 。
两人因此与发明电子显微镜的卢斯卡一起分享了1986年诺贝尔物理学奖。
扫描隧道显微镜(STM )罗雷尔 H Rohler 宾尼希 G Binning扫描隧道显微镜(STM )因为隧道电流对探针与样品表面的距离十分敏感,若控制隧道电流 I T 保持不变,则针尖空间坐标的变化反映了样品表面原子阵列的几何结构及起伏情况。
电子云a自动测控系统数据处理及显示系统真空bU STM 能够显示被观测物表面原子排列的三维图像,横向( x 、y )分辨率已达到0.1nm ,纵向(z )分辨率达到0.01nm 。
xyzSTM使人类能够实时地观察单个原子在物质表面的排列状态,并可对单个原子和分子进行移动和操纵,在表面科学、材料科学、生命科学等领域的研究中有着广泛的应用。
物理学家正在调整一台STM1990年美国IBM公司的研究人员首先运用STM技术在金属镍表面移动35个氙原子,使它们排列成IBM字样,成功地实现了原子级的字母书写。
一维谐振子无论在经典领域,还是在微观领域,谐振子都是都是一个重要的物理模型弹簧振子xO x晶体中原子的振动质量为 的粒子在一维空间中运动,如果其势能函数可表示为m 22211()22U x kx m xω==k m ω=式中 称为角频率。
这称为一维谐振子。
22222d 12d 2m x E m x ψωψψ-+=谐振子的定态薛定谔方程 令: 、 、 ,则: ξαx =m αω=2λE ω=22d ()0d ψλξψξ+-=因求解过程比较复杂,下面仅分析求解的结果一维谐振子定态薛定谔方程的求解结果定态波函数2()2()e() (0,1,2,)x n n n x A H x n αψα-==()()n n H x H αξ=式中 是厄米多项式,是量子数 n 谐振子的能量11 (0,1,2,)22n E n n h n ων⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭=谐振子的能量——能量量子化1122n E n n h ων⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭=能级间隔 1Δn n E E E h ν+=-=一维谐振子对求解结果的分析0,1,2,n=量子数 0n =1n =3n =2n =Ox()U x 12h ν32h ν72h ν52h ν谐振子的能级图与普朗克的能量子假设一致基态能量(零点能)的存在,是量子力学的一个重要结果,也是微观粒子具有波动性的本质表现,被光的散射实验证实。
对求解结果的分析n =1n =3n =2n =Ox()U x 12h ν32h ν72h ν52h ν谐振子的能级图存在基态能量(零点能)02E h ν=比较:经典弹簧振子的能量212E kA=式中 称为厄米多项式 ()()22d 1d nnn nH e e ξξξξ-=-定态波函数2()2()e() (0,1,2,)x n n n x A H x n αψα-==概率密度函数 2()()n n p x x ψ=2()200()ex x A αψ-=2()211()ex x A x αψ-=222()222()(21)ex x A x αψα-=-对求解结果的分析谐振子的波函数曲线 和 概率密度曲线Ox1()p x Ox2()p x Ox0()p x 定态波函数2()2()e() (0,1,2,)x n n n x A H x n αψα-==式中 称为厄米多项式 ()()22d 1d nnn nH e e ξξξξ-=-Ox0()x ψ0n =Ox1()x ψ1n =Ox2()x ψ2n =Ox11()p x本节结束!谢谢观看!。