圆的基本图形结论

圆的基本知识点总结和公式圆是平面几何中最基本的几何图形之一。

它是由一个平面上距离固定点相等的点构成的集合。

本文将概述圆的基本定义、性质和公式，以及它在现实生活中的应用。

一、基本定义圆被定义为距离中心点固定距离的所有点的集合。

距离被称为半径（r），中心点被称为圆心（O）。

用符号表示圆。

二、圆的性质1.直径直径（d）是连接圆上两个相对点的线段，通过圆心。

它是半径的两倍，即d=2r。

2.周长周长（C）是圆上所有点到圆心的距离之和。

圆的周长公式是C=2πr，其中π（pi）表示一个圆的周长和直径之比，大约为3.14。

3.面积圆的面积（A）是圆内部的所有点的面积的总和，公式是A=πr²。

4.弧弧是圆上两个点之间的一段曲线。

圆的周长可以看作是一个完整的弧的长度。

5.扇形扇形是由圆心和两个相邻半径之间的弧形区域组成的图形。

圆的面积可以分解为若干个扇形的面积之和。

6.切线切线是从圆外一点画出的一条直线，它与圆相切于圆上一个点处。

切线与半径的长度相等。

7.圆弦圆弦是连接圆上两个点的线段。

如果一条弦穿过圆心，则被称为直径。

三、现实应用在现实生活中，圆形图案经常出现。

圆形的形状使得它非常适合用于实现运动和旋转。

以下是一些示例。

1. 轮胎轮胎是由圆形轮辋和圆形轮胎组成的。

轮胎的圆形轮廓使它可以在任何方向上旋转。

2. 模拟器游戏、飞行和汽车模拟器通常都有一个圆形的控制器。

圆形的形状使其易于操纵，可以随意改变方向。

3. 平盘秤平盘秤是一种由两个圆形盘组成的手持秤，遵循平衡原则。

当需要测量重量时，将物品放在一个盘子上，然后向另一个盘子上添加重量，直到两个盘子保持平衡。

4. 平面旋转圆形的形状也使得它非常适合在一个平面上做旋转运动。

这个概念被广泛应用于机械和电子工程，如发动机和电机。

四、结论在我们的日常生活中，圆形图案似乎无处不在。

可以想象一下，如果没有圆形，我们的许多设备和工具将无法如此有效地运作。

与其他几何形状相比，圆形的形状会导致许多有趣的性质和应用。

圆概念总结概述圆是平面几何中的一种特殊图形，它由平面上离定点一定距离的点构成。

圆是数学中的基本概念，具有许多重要的性质和应用。

基本概念圆的定义在平面几何中，圆被定义为到定点的距离等于半径的所有点的集合。

其中，定点称为圆心，半径表示任意一点到圆心的距离。

相关术语•弧度：圆上弧所对的圆心角的大小，用弧度来表示，它是角度的一种衡量方式。

•圆周：圆上所有点的集合，即圆的边界。

•直径：圆上任意两点之间通过圆心的线段。

•周长：圆周的长度，通常用C表示。

•面积：圆内部的区域的大小，通常用A表示。

基本性质半径性质•所有半径的长度相等。

•半径的长度等于直径的一半。

弧性质•相等的圆心角所对应的弧相等。

•大的圆心角所对应的弧大于小的圆心角所对应的弧。

角度性质•同弧度的两个圆心角相等。

•同弧度的圆心角所对应的弧长相等。

周长性质•周长与直径的关系：C = π × d。

•周长与半径的关系：C = 2 × π × r。

面积性质•面积与半径的关系：A = π × r^2。

圆的相关公式周长公式• C = π × d• C = 2 × π × r周长公式可以用来计算圆的周长，其中d表示直径，r表示半径。

面积公式• A = π × r^2面积公式可以用来计算圆的面积，其中r表示半径。

圆的应用圆是几何学中最常见的基本图形之一，它在日常生活和科学研究中具有广泛的应用。

工程应用•圆形道路的设计和施工。

•圆形水池或园林景观中的喷水池设计。

•圆形门廊或建筑物的设计和建造。

•圆形机械零件的加工和制造。

科学应用•圆的运动学研究，如行星、卫星等的轨道运动。

•圆的统计分析，如频率统计、时间序列分析等。

•圆的几何光学研究，如反射、折射等。

日常生活应用•圆形餐桌或咖啡桌的布局。

•圆形蛋糕或披萨的切割方法。

•圆形花圃或庭院的规划和设计。

•圆形运动场地的规划和建设。

结论圆是平面几何中的重要概念，具有许多重要的性质和应用。

圆的基本性质1．圆的有关性质：（1）圆是轴对称图形，其对称轴是任意一条过圆心的直线；圆是中心对称图形，对称中心为圆心．（2）垂直于弦的直径平分这条弦，并且平分弦所对的弧．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧．（3）弧、弦、圆心角的关系：在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．推论：在同圆或等圆中，同弧或等弧所对的圆周角相等；直径所对的圆周角是直角；900的圆周角所对的弦是直径．2．三角形的内心和外心:（1）确定圆的条件：不在同一直线上的三个点确定一个圆．（2）三角形的外心： （3）三角形的内心：3. 圆心角的度数等于它所对弧的度数．圆周角的度数等于它所对弧的度数一半． 同圆或等圆中，同弧或等弧所对的圆周角等于它所对的圆心角的一半．【例题精讲】例1． AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O 的半径为cm 3，则弦CD 的长为（ ）A ．3cm 2B ．3cm C． D ．9cm 例2、BC 是以线段AB 为直径的O ⊙的切线，AC 交O ⊙于点D ，过点D 作弦DE AB ⊥，垂足为点F ，连接BD BE 、．．（1）仔细观察图形并写出四个不同的正确结论：①___ ___，②___ _____ ，③_____ _，④________（不添加其它字母和辅助线） （2）A ∠=30°，CDO ⊙的半径r ．例3、如图，半圆的直径10AB =，点C 在半圆上，6BC =．（1）求弦AC 的长；（2）若P 为AB 的中点，PE AB ⊥交AC 于点E ，求PE 长．P B CEA 例3题图直线与圆、圆与圆的位置关系【知识梳理】1. 直线与圆的位置关系：2. 切线的定义和性质：3.三角形与圆的特殊位置关系：4. 圆与圆的位置关系：（两圆圆心距为d ，半径分别为21,r r ）相交⇔2121r r d r r +<<-； 外切⇔21r r d +=；内切⇔21r r d -=； 外离⇔21r r d +>； 内含⇔210r r d -<<【注意点】与圆的切线长有关的计算．【例题精讲】例1.⊙O 的半径是6，点O 到直线a 的距离为5，则直线a 与⊙O 的位置关系为（ ）A ．相离B ．相切C ．相交D ．内含例2. 如图1，⊙O 内切于ABC △，切点分别为D E F ，，．50B ∠=°，60C ∠=°，连结OE OF DE DF ，，，，则EDF ∠等于（ ）A ．40°B ．55°C ．65°D ．70°练习、1．⊙O 半径为6.5cm ，点P 为直线L 上一点，且OP=6.5cm ，则直线与⊙O •的位置关系是____2．如图，PA 、PB 分别与⊙O 相切于点A 、B ，⊙O 的切线EF 分别交PA 、PB 于点E 、F ，切点C 在弧AB 上，若PA 长为2，则△PEF 的周长是 _．3、如图，⊙M 与x 轴相交于点(20)A ，，(80)B ，，与y 轴切于点C ，则圆心M 的坐标是 。

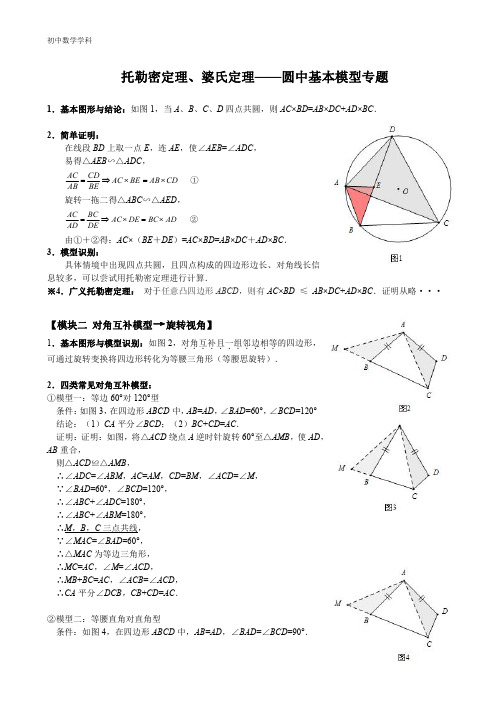
托勒密定理、婆氏定理——圆中基本模型专题1．基本图形与结论：如图1，当A、B、C、D四点共圆，则AC×BD=AB×DC+AD×BC．2．简单证明：在线段BD上取一点E，连AE，使∠AEB=∠ADC，易得△AEB∽△ADC，AC CD AC BE AB CD=⇒⨯=⨯①AB BE旋转一拖二得△ABC∽△AED，AC BC AC DE BC AD=⇒⨯=⨯②AD DE由①＋②得：AC×（BE＋DE）=AC×BD=AB×DC＋AD×BC．3．模型识别：具体情境中出现四点共圆，且四点构成的四边形边长、对角线长信息较多，可以尝试用托勒密定理进行计算．※4．广义托勒密定理：对于任意凸四边形ABCD，则有AC×BD≤AB×DC+AD×BC．证明从略···【模块二对角互补模型→旋转视角】1．基本图形与模型识别：如图2，对角互补且一组邻边相等．．．．．．．．．．．的四边形，可通过旋转变换将四边形转化为等腰三角形（等腰思旋转）．2．四类常见对角互补模型：①模型一：等边60°对120°型条件：如图3，在四边形ABCD中，AB=AD，∠BAD=60°，∠BCD=120°结论：（1）CA平分∠BCD；（2）BC+CD=AC．证明：证明：如图，将△ACD绕点A逆时针旋转60°至△AMB，使AD，AB重合，则△ACD≌△AMB，∴∠ADC=∠ABM，AC=AM，CD=BM，∠ACD=∠M，∵∠BAD=60°，∠BCD=120°，∴∠ABC+∠ADC=180°，∴∠ABC+∠ABM=180°，∴M，B，C三点共线，∵∠MAC=∠BAD=60°，∴△MAC为等边三角形，∴MC=AC，∠M=∠ACD，∴MB+BC=AC，∠ACB=∠ACD，∴CA平分∠DCB，CB+CD=AC．②模型二：等腰直角对直角型条件：如图4，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°．结论：（1）CA 平分∠DCB ；（2）CB +CD 2．证明：略···③模型三：等腰顶角120°对60°型条件：如图5，在四边形ABCD 中，AB =AD ，∠BAD =120°，∠BCD =60°．结论：（1）CA 平分∠BCD ；（2）CB +CD 3．证明：略···※④模型四：同侧双直角型条件：如图6，在四边形ABCD 中，AB =AD ，∠BAD =90°，∠BCD =90°．结论：CB －CD 2AC ．证明：略···【模块三对角互补模型→托密视角】1．等腰△三角函数计算：如图7，2cos 2cos BC AB m αα=⋅=⋅2．托勒密定理应用：①如图8，对角互补型：2cos 2cos ma mb c m a b c αα+=⋅⋅⇒+=⋅结论：当α=60°时，a ＋b =c当α=45°时，a ＋b 2当α=30°时，a ＋b 3※利用角平分线性质也可直接得2cos a b c α+=⋅②如图9，同侧等角型：2cos 2cos a m mb mc c b a αα⋅⋅+=⇒-=⋅结论：当α=45°时，c －b 2···【模块四婆罗摩笈多定理】婆罗摩笈多（约公元598－约660年）是一位印度数学家和天文学家，他出身于古印度的婆罗门种姓，婆罗门掌管着解释和预言天象的权力，掌握着天文学知识，以及测量和计算天体运行的工具——数学．婆罗摩笈多著有两部关于数学和天文学的书籍，他的一些数学成就在世界数学史上有较高的地位，他的负数及加减法运算仅晚于中国九章算术，而他的负数乘除法法则在全世界都是领先的．婆罗摩笈多还提出了著名的婆罗摩笈多定理，简称“婆氏定理”．若圆内接四边形的对角线相互垂直，则垂直于一边且过对角线交点的直线将平分对边．1．简单证明：已知：如图，四边形ABCD 内接于圆O ，对角线AC ⊥BD 于点M ，ME ⊥BC 于点E ，延长EM 交CD 于点F ，求证：F 是AD 中点．证明：∵AC ⊥BD ，ME ⊥BC∴∠CBD =∠CME∵∠CBD =∠CAD ，∠CME =∠AMF∴∠CAD =∠AMF∴AF =MF∵∠AMD =90°，同时∠MAD +∠MDA =90°∴∠FMD =∠FDM∴MF =DF ，∴AF =DF 即F 是AD 中点．2．婆罗摩笈多逆定理请你阅读婆罗摩笈多定理的证明过程，试证明婆罗摩笈多逆定理：（1）如图1，四边形ABCD 内接于圆O ，对角线AC ⊥BD 于点M ，F 为AD 中点，连接FM 并延长交BC 于点E ，求证：ME ⊥BC ．（2）如图2，△ABC 内接于圆O ，∠B =30°，∠ACB =45°，AB =2，点D 在圆O 上，∠BCD =60°，连接AD 交BC 于点P ，作ON ⊥CD 于点N ，连接并延长NP 交AB 于点M ，求证PM ⊥BA ，并求PN 的长．3．共顶等腰直模型（婆罗摩笈多模型）已知：如图，两个等腰直角三角形Rt △ABO 和Rt △CDO ，顶点重合，连接AC ，BD ．结论：①如果F 是AC 中点，那么一定有EF ⊥BD ；②如果EF ⊥BD ，那么一定有F 是AC 中点；③S △BOD =S △AOC ；④2FO =BD ．证明：（1）法一：（外）弦图构造法，如图1（2）法二：导角构造→全等构造法，如图2【例1】如图3所示,试证明：上述共顶等腰直模型中①②结论．【例2】如图，向△ABC的外侧作正方形ABDE、ACFG：（1）过A作AH⊥BC于H，AH与EG交于M，求证：①EM=MG，②BC=2AM．（2）若M为EG的中点，求证：AH⊥BC．【模块四真题探究】【例3】（改编）如图1，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状，并说明理由；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于 AB的什么位置时，四边形APBC的面积最大?求出最大面积．【例4】（2013·成都中考改编）如图2，A ，B ，C 为⊙O 上相邻的三个n 等分点， AB BC=，点E 在 BC 上，EF 为⊙O 的直径，将⊙O 沿EF 折叠，使点A 与A'重合，点B 与B'重合，连接EB'，EC ，EA'．设EB'=b ，EC =c ，EA '=p ．现探究b ，c ，p 三者的数量关系：发现当n =3时，p =b +c ；请继续探究b ，c ，p 三者的数量关系：当n =4时，p =__________；当n =8时，p =__________；当n =12时，p =__________．（参考数据：62sin15=cos 75=4-︒︒，62cos15=sin 75=4+︒︒）本讲反思：。

圆的基本概念与相关定理圆是数学中非常重要的几何图形之一，它具有独特的形状和性质。

在本文中，我们将介绍圆的基本概念以及与之相关的定理。

通过深入理解圆，我们能够更好地应用它们解决实际问题，并在数学学习中掌握圆的性质。

一、圆的基本概念圆是由平面上与一个确定点的距离恒定的所有点组成的集合。

这个确定点被称为圆心，与圆心距离相等的点构成的线段被称为半径，圆内部的区域被称为圆的内部，圆外部的区域被称为圆的外部。

基于这些概念，我们可以得出以下结论：1. 圆的半径相等的两个圆是相等的。

2. 圆的直径是通过圆心，并且等于两个半径的和。

3. 圆的弧是连接圆上两个点的一段弧线。

4. 圆的圆周角是以圆心为顶点的角，其对应的弧长与半径之比等于360°与2π的比值。

二、圆的相关定理圆的特性使其具有许多重要的定理，下面我们将介绍其中一些常见的定理：1. 圆心角定理在圆的圆周上，相交弦对应的圆心角相等。

2. 弧长定理相等的圆心角所对应的弧长相等。

3. 切线定理如果一条直线与一个圆相切，那么与切点相连的半径垂直于切线。

4. 弦切角定理圆内一条弦上的切线和这条弦所对应的角相等。

5. 直径角定理直径所对的圆心角是直角。

6. 弧的交角定理相交弦所对应的弧的交角等于这两个弧所对应的圆心角的一半。

通过学习和应用这些定理，我们可以解决各种与圆相关的问题，比如计算弦长、弧长、角度等。

总结：通过本文，我们了解了圆的基本概念和一些相关的定理。

深入理解圆的性质和定理，不仅可以帮助我们解决数学问题，还可以在解决实际问题时提供有效的思路。

因此，在学习数学时，我们应该注重圆的概念和定理的理解，并善于运用它们。

通过对圆的学习，我们不仅能够提高数学水平，还能够培养我们的逻辑思维能力和问题解决能力。

圆作为数学中的重要概念之一，在几何学、物理学等领域都具有重要的应用价值。

希望大家能在学习中对圆有更深入的认识，进一步掌握和应用圆的性质与定理。

这将有助于我们在数学学习中取得更好的成绩和提高思维能力。

九年级圆的知识点基本图形在九年级数学学习中，我们将遇到许多基本图形，其中一个重要的基本图形就是圆。

圆在我们的生活中随处可见，无论是物体的形状，还是几何学问题，圆都占据着重要的地位。

在学习圆的知识点时，我们将从它的定义、性质以及相关公式等方面展开讨论。

第一部分：圆的定义与特性圆的定义非常简单，它是由平面上的一点到另一点的所有点的集合所组成的。

圆由一个中心点和一定半径的长度所确定。

在数学中，我们用O表示圆的中心点，用r表示圆的半径。

除此之外，圆还有以下几个重要的特性：1. 圆是平面上曲线长度最短的封闭曲线。

这意味着，如果我们需要围住一块最大的面积，那么我们应该选择圆形。

2. 圆的直径是通过圆心的任意两点之间的距离，而半径则是从圆心到圆上的任意一点的距离。

直径的长度是半径的两倍。

3. 在圆上，任意两个点间的连线被称为弦。

如果弦通过圆心，我们称之为直径。

第二部分：圆的面积与周长圆的面积和周长是九年级数学中与圆相关的两个重要概念。

了解如何计算圆的面积和周长对于解决与圆有关的问题至关重要。

1. 圆的面积：圆的面积可以表示为πr²，其中π是一个常数，接近3.14159。

要计算圆的面积，我们只需要将π乘以半径的平方即可。

2. 圆的周长：圆的周长也被称为圆的周长，它可以通过公式2πr计算得出。

即将半径乘以2π即可。

第三部分：圆与锥体、圆柱体和圆锥的关系在九年级的数学学习中，我们不仅需要了解圆本身的知识，还需要了解圆在三维空间中的应用。

圆与锥体、圆柱体和圆锥有着密切的关系。

1. 圆锥：圆锥是由一个圆形底部和一个顶点连接而成的三维图形。

圆锥的体积可以通过公式V = (1/3)πr²h计算得出，其中r是底部圆的半径，h是圆锥的高。

2. 圆柱体：圆柱体由两个平行的圆面和连接它们的曲面所组成。

圆柱体的体积可以通过公式V = πr²h计算得出，其中r是底部圆的半径，h是圆柱体的高。

3. 锥体：锥体是由一个圆锥和一个平面切割而成的图形。

研究报告圆研究报告：圆一、引言圆是几何学中的一种基本图形，它具有许多独特的性质和应用。

本研究报告旨在深入探讨圆的定义、性质和应用，并分析其在实际生活中的重要性。

二、定义1. 圆的定义在几何学中，圆被定义为一个平面上所有距离中心点相等于半径的点的集合。

即圆由中心和半径唯一确定。

2. 圆周和弧长圆周是指围绕圆形边界的长度，而弧长是圆弧的一部分的长度。

三、性质1. 圆的性质（1）等边性：圆上任意两条弦等长。

（2）正多边形的内接圆：正n边形内外接圆的外接圆与内接圆相切。

（3）切线性：切线与半径垂直。

2. 圆的计算公式（1）圆的周长：2πr，其中r为半径。

（2）圆的面积：πr^2，其中r为半径。

四、应用圆在很多领域都有广泛的应用。

1. 圆在建筑设计中的应用在建筑设计中，圆经常用于设计圆形的建筑物和装饰物。

比如大型圆形剧场、圆形广场和圆形雕塑等。

2. 圆在工程设计中的应用在工程设计中，圆常用于设计各种旋转部件，如齿轮、风车和涡轮机组等。

圆的性质使得它们具有良好的旋转平衡性和稳定性。

3. 圆在数学研究中的应用圆是数学研究中重要的基本图形之一，它在数学分析、几何学和代数学等领域都有广泛的应用。

例如，圆的性质和变换常常用于函数图像的分析和研究。

五、结论通过对圆的定义、性质和应用的研究和分析，我们可以得出以下结论：1. 圆是几何学中的重要图形之一，具有独特的性质和应用价值。

2. 圆在建筑设计、工程设计和数学研究等领域都有广泛的应用。

3. 进一步研究圆的性质和应用，将有助于推动相关领域的发展和创新。

六、参考资料1. 林维苏. 几何基本知识[M]. 北京：人民教育出版社，2010.2. Xiong, Y., & Chan, A. B. (2015). Geometry reading and understanding: A survey. ACM Computing Surveys (CSUR),46(2), 24.3. 王立荣. 数学建模中的圆及其应用[J]. 中国高中数学教学，2008(5): 32-34.。