第七章 三角形复习课2
- 格式:ppt
- 大小:776.50 KB
- 文档页数:20
![第七章三角形复习课[下学期]--新人教版-(新编201912)](https://img.taocdn.com/s1/m/d6327e3379563c1ec5da71c7.png)
第七章 三角形复习教案(2课时)数学组 文东复习目标1、理解三角形及有关概念,会画任意三角形的高、中线、角平分线;2、了解三角形的稳定性,理解三角形两边的和大于第三边,会根据三条线段的长度判断它们能否构成三角形;3、会证明三角形内角和等于180,了解三角形外角的性质。
4、了解多边形的有关概念,会运用多边形的内角和与外角和公式解决问题复习重点:三角形三边关系、内角和,多边形的外角和与内角和公式、镶嵌。
难点:三角形内角和等于180的证明,根据三条线段的长度判断它们能否构成三角形及简单的平面镶嵌设计。
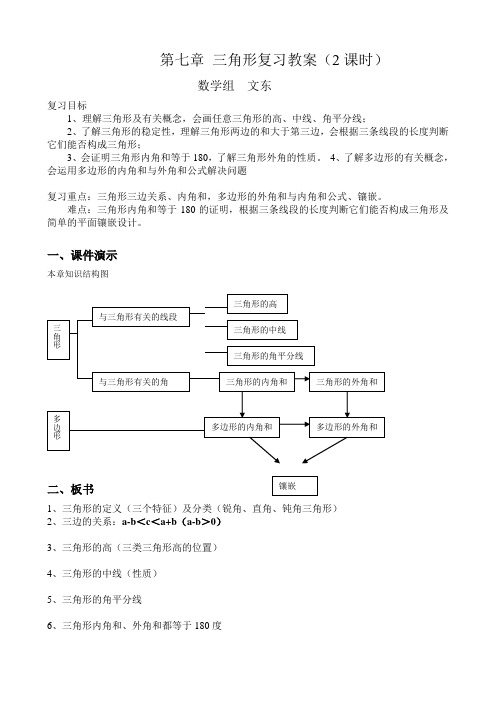
一、课件演示本章知识结构图二、板书1、三角形的定义(三个特征)及分类(锐角、直角、钝角三角形)2、三边的关系:a-b <c <a+b (a-b >0)3、三角形的高(三类三角形高的位置)4、三角形的中线(性质)5、三角形的角平分线6、三角形内角和、外角和都等于180度7、内角和公式:(n-2).180∙,简单推理8、任意多边形外角和:360度9、镶嵌三、基础过关1.下列条件中能组成三角形的是()A、5cm,7cm,13cmB、3cm,5cm,9cmC、6cm,9cm,14cmD、5cm,6cm,11cm2.三角形的两边为7cm和5cm,则第三边x的范围是_______________________.3.等腰三角形的两边为7cm和5cm,则三角形的周长是_____________.4.下列能说明∠1>∠2的是( )5.如图所示:△ABC中,D,E分别为BC,AD的中点,且△ABC面积为4,则阴影部分面积为_____四、作业21121212 A B DC第二课时一、例题讲解1.如图△ABO 与△CDO 称为“对顶三角形”,你能证明∠A+ ∠B= ∠C+ ∠D 吗?2、如图(3),在△ABC 中,∠ABC 与∠ACB 的平分线相交于0,那么∠BDC =90°+ ∠A ,你会说明这个结论正确吗?3.∠CAD+ ∠B+ ∠C+ ∠D+ ∠E=( 三种情况 )二、巩固练习1.三角形两边长分别为2cm ,6cm ,且周长是奇数,则第三边长是 () 2.如下图,则ABC 的形状是( )A 、锐角三角形B 、钝角三角形C 、直角三角形D 、等腰三角形E B DCBA O3a 2a aB AC EBAD CF3.如上图, ∠A+∠B+∠C+∠D+∠E+∠F= ;4.AB ∥CD, ∠A=45°∠C=80°,求∠M 的度数.5.如图,直线DE 与△ABC 的三边所在直线交与D 、E 、F, ∠ A=40°, ∠ D=25°,DE ⊥AB,求∠ ACB 的度数.6. △ABC 中∠B=80°,E 为AC 上一点,ED ⊥BC 于D ,DF ⊥AB 于F ,则∠EDF=( )三、作业 M B A D C EB AD C FC。

《第七章三角形》复习教案(预习+展示)知识结构:一、你认为本章知识必须识记的知识有:(结合图示说明)定理:公式:作法二、互相对照,尽量将内容一完善。
三、互相背诵,看那个组最先全部完成。
四、知识运用:解答如下问题,先独立解答,有困难的可合作解答,解答时注意一题多解及不要漏解。
三角形三边关系的应用1、三角形三边长分别为6、9、x,则x的取值范围是什么?2、等腰三角形两边长分别为5和7,求其周长。
若两边长为3和7呢?3、如图,在等腰△ABC中,AB=AC,一腰上中线BD将这个三角形的周长分为16和8的两部分,求这个等腰三角形的腰长与底边长。
(用方程思想解决)三角形内角和定理及推论的应用4、如图在△ABC中,DE∥BC,DBE=30,EBC=25,求BDE的度数。
5、如图,B处在A处的南偏西45方向,C处在A处的南偏东15方向,C处在B处的北偏东80方向,求ACB。
6、如图,求B+D+E的度数。
7、等腰三角形两内角度数比为1∶2,则该等腰三角形的顶角为多少?(用方程思想,别漏解!)8、如图,△ABC中,A=50,BD、CD分别平分ABC、ACB,求D 度数。
9、如图,△ABC中,C,FDBC,DEAB,AFD=152,求EDF。
10、已知非直角△ABC中,A=45,高BD和CE所在直线交于H,求BHC的度数。
画出图形,你发现能得出几种结论呢?三角形外角定理及推论的应用11、如图,证明:BDC=C+A。
收集一下你们小组有几种证法。
哪种最好?12、如图,△ABC中,CDAB,BEAC,A=50,求BFC度数。
13、如图,AD、AE分别为△ABC的高线与角平分线,且B>C,求证:DAE=1/2(C),当图形变化为2、3时,结论如何?14、如图,ABC、ACB的平分线交于点O,ABC的平分线与ACB 的外角平分线交于点D,ABC与ACB的相邻外角平分线交于点E,求证:D=1/2A。
在此基础上,探求BOC与E与A的数量关系。
![第七章三角形复习课[下学期]--新人教版-2020-0926](https://img.taocdn.com/s1/m/9fa8c8e2ad02de80d5d84091.png)
![第七章三角形复习课[下学期]--新人教版-](https://img.taocdn.com/s1/m/4b3a1159551810a6f52486e2.png)

人教版七年级下第七章“三角形”复习课()——“与角有关的三角形复习课”教学设计方案一、教学目标:通过复习“与角有关的三角形”知识点,进一步领会建模、有序思维、数形结合、分类、化归、从特殊——一般——特殊等数学思想,体会事物之间相互联系和运动变化、量变引起质变等辩证唯物主义观点:同时培养学生分析问题、解决问题能力,培养学生学习数学的乐趣;体现“探究有尺度,归纳有顺序,习题有难易,精彩有延续”.二、教学重点、难点:教学重点:有序思维、数形结合教学难点:动点问题教学手段:多媒体课件教学方法:探究式互动性教学三、教学过程一.温顾新知,巩固认知.三角形内角和三角形内角和等于度直角三角形的两个锐角互余。
.三角形外角和三角形的三个外角的和是°.三角形的外角与内角的关系三角形的一个外角等于与它不相邻的两个内角的和.三角形的一个外角大于与它不相邻的任何一个内角.. 三角形的分类() 按角分三角形 直角三角形 斜三角形 锐角三角形钝角三角形 () 按边分三角形 不等边三角形 等腰三角形 底和腰不等的等腰三角形 等边三角形 二、应用新知,深化认知.根据下图已知角的度数,求的值.⎧⎨⎩⎧⎨⎩⎧⎨⎩⎧⎨⎩() () (). 在△中,∠∠∠,则∠°,∠ ° 。
.在△中 若∠:∠:∠ ::,则∠°,∠ ° 。
小结:求三角形角的一般方法。
由形定数,由数思形,数形结合,方程思想。
三、应用新知,活化认知.已知等腰三角形的一个内角为°,则其顶角为( ).° .° .° .°或°. 等腰三角形的一个外角为°,则它的底角为( )° ° °或° .以上都不对小结:等腰三角形的角的求法,体现分类思想.四、应用新知,升华认知.有一块直角三角尺,放在△上,如图所示,△的两条直角边、分别经过、两点,在△中,∠ 求∠∠的度数;问题:若∠(锐角),其它条件不变, 求∠∠的度数;问题:若∠(钝角)呢?问题:探究∠、∠、∠与∠ 之间的数量关系.变式二:若点在△的外部,两条边、仍过、两点,∠∠∠∠是否还成立?请画出图形,探究∠、∠、∠与∠ 之间的数量关系?特例:若点是△中∠ 、∠ 的角平分线交点,试探究∠与∠ 之间1902D ∠=︒+∠A的数量关系.答案:特例: 若点是∠的角平分线与∠ 的外角平分线的交点,试探究∠与∠ 与之间的数量关系.答案: 特例: 若点是∠的外角平分线与∠的外角平分线的交点,试探究∠与∠ 与之间的数量关系.答案: 变式三: 若将△的两条边、分别经过、两点,改为△的两条边、分别与△两条边、相交,以上探究的结论是否还成立?小结:数学的解题方法:从特殊——一般——特殊.五:归纳总结,反思提炼 本节课,你有什么收获?还有什么困惑? 学习数学常用有序思维、数形结合、分类、从特殊——一般——特殊等数学思想,解题时学会多思、多想、多动,学起数学感觉趣味无穷.教学反思本节课为复习课,为了区分复习课和习题课,整节课贯穿了由形定数,由数思形,数形结合,方程思想、有序思维、分类讨论、从特殊——一般——特殊等重要数学思想,从学生最熟悉的简单习题入手,再层层提升问题难度,培养学生思考的逻辑性。