第5章 FE模型
- 格式:ppt
- 大小:291.00 KB
- 文档页数:47




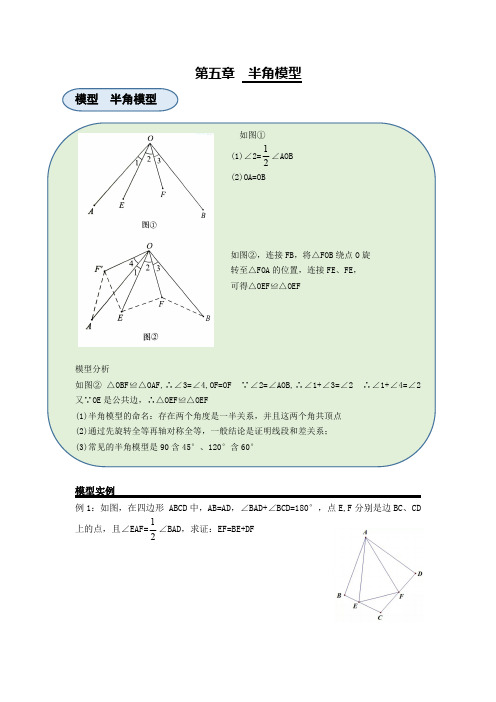
第五章半角模型模型半角模型如图①(1)∠2=21∠AOB (2)OA=OB如图②,连接FB,将△FOB 绕点O 旋转至△FOA 的位置,连接FE、FE,可得△OEF≌△OEF模型分析如图②△OBF≌△OAF,∴∠3=∠4,OF=OF∵∠2=∠AOB,∴∠1+∠3=∠2∴∠1+∠4=∠2又∵OE 是公共边,∴△OEF≌△OEF(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点(2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系;(3)常见的半角模型是90含45°、120°含60°模型实例例1:如图,在四边形ABCD 中,AB=AD,∠BAD+∠BCD=180°,点E,F 分别是边BC、CD 上的点,且∠EAF=21∠BAD,求证:EF=BE+DF(一)、半角结构之90°与45°例2、如图,在正方形ABCD中,M,N分别在BC,CD上,∠MAN=45°,(1)求证:MN=BM+DN(2)作AH⊥MN于点H,求证:AH=AB经典练习1.如图,在正方形ABCD中,E,F分别在BC,CD上,∠EAF=45°,BE=2cm,DF=3cm,求正方形的边长2.如图,在△ABC中,∠BAC=90°,AB=AC,点D,E是边上两点且∠DAE=45°,求证:BD2+CE2=DE23.如图,在正方形ABCD中,点E、F分别在边CD、BC的延长线上,且∠FAE=45°,试探究EF、BE、DF之间的数量关系,并证明.4.如图,在正方形ABCD中,点E,F分别是边BC、CD上的动点(不与B,C,D重合),且∠EAF=45°,对角线BD分别和AE、AF交于点M、N连接NE,求证:△ANE是等腰直角三角形(二)、半角结构之120°与60°例2.在等边△ABC的两边AB、AC上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC。

i
铁的四种超导体结构:(a)LaFeAsO ;(b)SrFe2As2;(c)LiFeAs;(d)Fe1+xTe.从正方相到正交相的结构相发生之后母体也会进入到反铁磁态。
(a)(b)中也包括了这种反铁磁结构。
注意Fe1+xTe 中额外的x的铁在Fe(2)的位置,并未填满。
Fe Al接触表面的建模1.该模型由Fe的(100)面与砧的(200)面搭配构成界面,经计算此界面模型错配度仅为3.04678×10~,根据HONG等人的计算【6J6,在界面处匹配表面错配度很小的情况下,可以认为界面是完全匹配,对计算结果影响很小.此模型有32个原子,由于原子个数太多,为了分析方便,在本文对界面附近的原子进行编号.微合金化元素均为替位型杂质,分别替换模型中标号为l的础原子和标号为8的铁原子.在计算中,采用能量最小化方案对Fe与~的层间距进行了优化.计算采用CA跚忑P(Ca耐晡age Serial TotalEnergy Package)[7J软件,选择广义梯度近似(GGAIs】)下的PBE泛函描述交换能,平面波截止能均取为350 eV,布里渊区的K点取为5×5 x 2,收敛精度控制在10一eV/atom,
Fig. 1. Crystal structure of Ti4Fe2O oxide: O–small balls, Fe–middle
balls, Ti–large balls. i。