空间机构的自由度计算资料讲解

02
机构自由度的基本概念
定义与分类
定义
机构自由度是指在给定机构中， 通过确定各构件的位置和姿态， 能够独立改变的坐标数目。
分类
根据机构自由度的性质，可分为 平面机构自由度和空间机构自由 度。
自由度的计算公式
平面机构自由度计算公式
$F = 3n - 2p_{r} - p_{h}$
空间机构自由度计算公式
三杆机构自由度计算
总结词：计算方法多样 总结词：参数影响 总结词：工程应用
详细描述：三杆机构自由度的计算方法有多种，包括解 析法、图解法和经验公式法等，需要根据具体情况选择 合适的方法进行计算。
详细描述：在三杆机构自由度计算中，需要考虑多个参 数的影响，如活动构件数、低副数、高副数以及机构中 是否存在局部自由度或虚约束等情况。
它反映了机构在空间中的运动状 态，是机构分析和设计中的重要 概念。
机构自由度计算的意义
机构自由度计算是机构分析和设计的基础，通过计算自由度可以了解机构的运动特 性和能力。
机构自由度计算有助于确定机构的可达工作空间、运动速度和加速度等性能指标。
机构自由度计算还可以用于机构的优化设计和改进，提高机构的运动效率和稳定性 。
机构自由度与动力学关系研究
总结词
机构自由度与动力学关系是机构学领域的重要研究方向，需要深入研究其内在联系和规 律。
详细描述
机构自由度与动力学关系是机构学领域的重要研究方向，研究它们之间的内在联系和规 律有助于更好地理解机构的运动特性和动力学行为。未来需要加强这方面的研究，为机
构设计和优化提供更加科学的依据。
代数法
代数法的步骤
1. 列出所有约束条件和运动变量。
2. 建立代数方程来表示各约束条件和运动变量 之间的关系。

机械故障诊断
通过运动分析诊断机械故障的原因 和位置。
控制系统设计
利用运动分析结果设计控制系统的 参数和策略。
机构运动分析的实例
平面四杆机构的运动分析
01
通过解析法计算平面四杆机构的自由度，并分析其运动特性。
凸轮机构的运动分析
02
利用实验法测量凸轮机构的位移、速度和加速度，分析其运动
规律。
机器人臂关节的运动分析
03
通过数值法模拟机器人臂关节的运动行为，优化关节的设计参
数。
04
机构动力学分析
机构动力学的基本概念
机构动力学是研究机 械系统中机构运动及 其与力的关系的学科 。
机构动力学的基本概 念包括力、力矩、加 速度、速度和位移等 。
它涉及到系统的平衡 、运动规律、动态响 应等方面的内容。
机构动力学分析的Байду номын сангаас法
空间机构自由度计算
总结词
空间机构自由度计算是机械原理中一个复杂的概念，它涉及到机构在空间中的 运动自由度数。
详细描述
空间机构的自由度计算公式为F=6n-(3PL + Ph)，其中n为活动构件数，PL为低 副数，Ph为高副数。与平面机构不同，空间机构需要考虑三个方向的自由度， 因此计算更为复杂。
特殊机构自由度计算
通过建立平面连杆机构的运动学和动力学模型，分析其运动规律 和动态响应。
凸轮机构的动力学分析
研究凸轮机构的动态行为，包括从动件的运动规律和受力情况等。
齿轮机构的动力学分析
分析齿轮机构的动态特性，如振动、冲击和噪声等，以提高齿轮传 动的平稳性和可靠性。
05
机构优化设计
机构优化设计的目标和方法
目标

F>0,
原动件数<F，运动不确定
原动件数>F，机构破坏
– 综上所述可知，机构具有确定运动的条件是：机 构的自由度F>0且等于原动件数。
分析：这是一对心尖顶凸轮机构，可动件数目为2，低副2个， 高副1个，所以其自由度为：
F=3n-2PL-2PH =3×2-2×2-1＝1
注意：一般情况下，桁架在机构 分析中作为一个构件(结构体)来对 待。
B Aq yA
作平面运动的刚 体有三个自由度
（三个坐标参数 才能确定其位置）
xA
低副的引入减 少两个自由度
x
q
高副的引入减少 一个自由度
y f (x)
沿法线方向不能运动
综上所述，平面机构中， 每个低副引入两个约束， 使构件失去两个自由度； 每个高副引入一个约束， 使构件失去一个自由度。
1.2.2
先看例子：按照之前的算法下图机构的自由度为
F=3n－2PL－PH=3×8－2×11－1=1 或 F=3n－2PL－PH=3×8－2×10－1=3
为什么？
局部自由度
定义——在某些机构中，
不影响其他构件运动的自 由度称为局部自由度。
处理办法——把滚子固化
在支承滚子的构件上。
复合铰链
定义——两个以上的构件在同一处以转动副联接，则构成
复合铰链。
处理办法——m个构件在同一处构成转动副，实际转动副
数目为（m-1）个。
N-1个转动副
计算机构自由度时应注意的问题
复合铰链
两个以上的构件在同一处以转动副 联接所构成的运动副。
解决方案 k 个构件在同一处构成复合铰链， 实际上构成了 ( k-1 ) 个转动副。
1

由m个构件组成的复合铰 链，共有(m-1)个转动副。
1
复合铰链数=构件数-1
1
2
3
2
3
一、复合铰链
F 3n 2 pl ph
复合铰链——由个m构件在一处 组成轴线重合的转动副。
24
C
3
实际有(m-1)个转动副。 F=3×5-2×6=3 ？ F=3×5-2×7=1
B2
3 A1
D
4 E 5
6
如图所示F、B、D、C处是复合铰链
内燃机
键 轴
齿轮
机构的组成(2/16)
空间运动: 6个自由度 一个自由构件
平面运动: 3个自由度
2.运动副
机构的组成(3/16)
运动副 是两构件直接接触而构成的可动连接；
运动副元素是两构件参与接触而构成运动副的表面。
约束 两构件上组成运动副时相对运动受到限制，这种对 独立运动的限制称约束
自由度减少数目等于约束数目。引入约束数目与运动副种 类有关。根据引入约束数目分Ⅰ、Ⅱ……Ⅴ级副。
构件与零件的区别： 构件是运动单元体 零件是加工制造单元体
构件——运动单元体。
零件——制造单元体。
构件是由一个或若干个零件组成刚性系统。
固定构件——机架
构件
活动构件 主动件 从动件
主动件（或原动件。）
作用有驱动力（矩）的活动构件称为
输入运动或动力的主动件称为输入件。 输出运动或动力的从动件称为输出件。
此机构能动，须给定一个原动件
4）
n=4 pl=5 ph=1 p’=0 F’=0
F=3n-(2pl+ph-p’)-F’ =3*4-(2*5+1-0)-0=1
复合铰链：A(2)

平面机构的组成原理、结构分类及结构分析(2/4)
（1）基本杆组的条件 3n－2pl－ph＝0
式中n、pl及ph分别为基本杆组中的构件数、低副数和高副数。 全为低副杆组的条件
3n－2pl＝0 （2）杆组的基本类型
或 n/2＝pl/3
1）Ⅱ级杆组 由2个构件和3个低副构成的杆组。
B
12
A
C
a)
B2
1
C
§2-5 机构自由度的计算
1.平面机构自由度的计算
（1）计算公式
F＝3n－(2pl＋ph)
式中：n为机构的活动构件数目； pl 为机构的低副数目； ph为机构的高副数目。
(2)举例 1）铰链四杆机构 F＝3n－(2pl＋ph)
＝3×3－2×4 －0 ＝1
2）铰链五杆机构
F＝3n－(2pl＋ph) ＝3×4－2×5 －0 ＝2
（1）轨迹重合的情况 在机构中，如果用转动副连接的是
两个构件上运动轨迹相重合的点，该连 接将带入1个虚约束。
例如椭圆仪机构就是这种情况（图 中：∠CAD＝90°，BC＝BD）。
显然，转动副C所连接的C2、C3两点 的轨迹重合，将带入一个虚约束。
（2）用双副杆连接两构件上距离恒定不变的两点的情况
在机构运动过程中，如果两构件上两点之间的距离始终保持 不变， 若用一双副杆将此两点相连，也将带入一个虚约束。
i=m+1
由上式可知，公共约束m=0,1,2,3,4。故相应的机构分别 称为0族、1族、2族、3族、4族机构（五类）。
例2-6 楔形滑块机构
解 因此机构为全移动副平面机构，故 m＝4，则
F＝(6－m)n－(5－m)p5 ＝(6－4)×2－(5－4)×3 ＝1

§1-2 空间机构的结构综合
1、单自由度平面机构的结构综合
研究一定数量的构件和运动副可以组成多少机构型 式的综合过程。实质是排列与组合的数学问题。可利用 图论和矩阵工具研究。
单自由度的低副机构是由具有4个自由度的运动链 所组成，自由度为4的运动链应满足下列关系：
(1) n2=4, n3=4 (2) n2=5, n3=2, n4=1 (3) n2=6, n4=2
而成的系统。 闭式链——组成一个或多个封闭形的运动链。 开链——不可组成封闭形的运动链。
简单运动链——运动链中可出现与其它三 个构件相连的构件时。如图a、b、c，否则 称为复杂运动链，如图d。
运动链的自由度——独立相对运动的个数 或各构件相互位置变化所需自由参数（广 义坐标）的个数。例如上图a四个运动参数 θ1、θ2、θ3、θ4中只有一个自由参数（如 θ1）F=1，上图b三个运动参数θ1、θ2、θ3 均为自由参数，F=3。
3、空间单封闭形单自由 度机构的结构综合
1）当λ=6，如表综合可 得12种类型433种机构。
2）综合四杆单封闭形机 构，可得3种类型138 种机构。其中9种具有 特殊实用价值。
3）构成闭合约束数小于 6的机构时，组成条件 需要严格遵守，否则 可能出现不能运动的 刚架。
还有特殊的三类： R-R-R-R R-S-S-R R-C-C-R
Ⅴ级副——约束度为（5－m）
Ⅳ级副——约束度为（4－m）
……
当m=0（零族机构）即可加任何公共约束， 机构自由度计算公式用（1－1）。
m=1（一族机构）不可能 P2 （1－4）
m=2（二族机构）不可能存在Ⅰ、Ⅱ级副
F 4n 3P5 2P4 P3 （1－5）
F 6n 5P5 4P4 3P3 2P2 P1 （1－1）

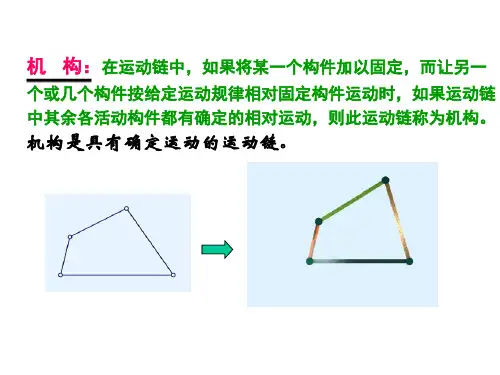
机构自由度的概念
机构自由度（Degree of Freedom, DoF）是机械原理中的一个核心概念，它描述了一个机构在没有外力或驱动力作用下能够独立完成的运动的数量。

具体来说：
机构自由度定义：
在一个机械机构中，为了确定该机构所有构件的相对位置和姿态，所需要的独立运动参数的数量称为机构的自由度。

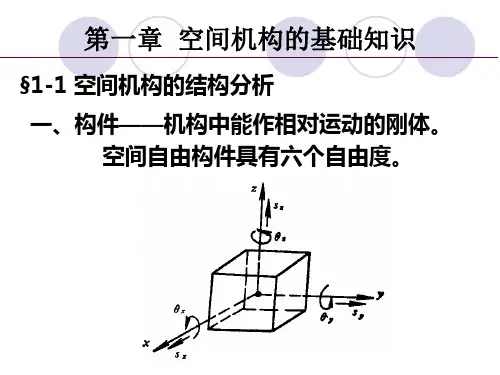
- 对于单个构件而言，在三维空间中，它有6个自由度，包括沿三个正交方向（X、Y、Z轴）的平动自由度以及绕这三个轴的转动自由度。

- 当多个构件通过运动副（如铰链、滑块等）相互连接组成机构时，由于运动副对构件的约束作用，实际的机构自由度会小于各个独立构件自由度之和。

- 机构的总自由度计算公式为：总自由度= 各构件自由度之和- 约束数（即由运动副引入的约束数目）。

- 在实际应用中，如果机构具有一个或多个原动件（例如电机、气缸等驱动部件），并且原动件提供的独立输入变量与机构自由度相
匹配，则机构可以实现确定的、预设的运动。

平面机构自由度通常指机构在二维平面内的自由度，一般包括沿两个正交方向的移动自由度及一个绕垂直于平面轴的转动自由度。

总结来说，机构自由度是评价机构运动特性的重要指标，对于设计和分析机械设备有着至关重要的意义。

只有当机构的自由度等于零时，机构才是完全刚性固定的结构；而具有至少一个自由度的机构才能够产生相对运动，并可能成为有用的机械装置。

2-6、计算自由度时的注意事项
• 1、复合铰链 • 三个构件以复合铰链
联接，则有两个转动 副。 • M个则有M-1个转动副。 • 画法
2、局部自由度
• 凸轮为主动件转动， 推杆从动，为了减小 磨擦，磨损，安装滚 子，改滑动为滚动。
f 3n 2 pl ph 33 231 2
五，运动副的画法
• 机架 • 投影方向不
同
2-3，机构运动简图
• 分析与设计均需要画出机构运动简图 • 根据机构的尺寸按比例定出各个运动副的
位置，用运动副的代表符号和线条把机构 表示出来。 • 目的…运动、动力分析，综合设计 • 机构示意图…不严格按比例画
2-4机构具有确定运动的条件
• 确定运动…当机构的原动件按给定的运动 规律运动时，该机构中的其余构件的运动 也是完全确定的
空间运动副
运动副画法
二、构件
• 机架 • 二副构件 • 三副构件 • 四副构件、多副构件
• 三、运动链 将构件（两个以上）用运动副联接起来，成为运 动链
封闭链，首尾相接
开式链…至少有一个构件只包含一个副。 • 四、机构…将运动链中的某一构件固定成为机架，
则这种运动链便成为机构
原动件…机构中按已知运动规律运动的构件 从动件…除原动件外的活动构件为从动件 平面机构、空间机构、球面机构
• 运动副元素…运动副中参与接触的 部分， 即：点，线，面
平面、球面、圆柱面、曲面、曲线、 直线等
运动副分类，
• 按引入约 束…级别 1-5级
• 或剩余自 由 度 …5-1 类
• 按接触情况即运动副元素（面、线、点） 分为
低副…面接触，接触应力较低 高副…点、线接触，接触应力较高 • 按平面、空间运动分为 平面运动副

空间连杆机构自由度的计算
一、空间闭链机构的自由度 二、空间开链机构的自由度 三、计算机构自由度应注意的事项

一、空间闭链机构的自由度
n个可动构件
Ⅰ类运动副 5个约束 Ⅱ类运动副 4个约束 Ⅲ类运动副 3个约束 Ⅳ类运动副 2个约束 Ⅴ类运动副 1个约束

6n自由度
p1个Ⅰ类副 p2个Ⅱ类副 p3个Ⅲ类副 p4个Ⅳ类副 p5个Ⅴ类副
5p1个约束 4p2个约束 3p3个约束 2p4个约束 p5 个约束
机构自由度 =
各可动构件 自由度之和
各类运动副提供 的约束数目总和
空间闭链机构自由度的公式:
F 6n p

i 1
p
fi
单环闭链机构的自由度公式：
F
fi 6
i 1
p
二、空间开链机构的自由度
开链机构的可动构件数目 = 运动副数目,即n = p
开链机构的自由度计算公式:
F

i 1
p
fi
开链机构的自由度 =
三、计算机构自由度应注意的事项
1. 公共约束
2. 消极自由度fp
3. 局部自由度ft
1.公共约束
表现形式: 常用m表示
闭链机构
末杆拆开后
开链机构
机构自由度(考虑公共约束)公式应为：
F fi 6 m
i 1
p
公共约束的判别原则：
特殊对待具体的情况
2.消极自由度fp 概念: 机构中的一些不起运动学作用的自由度 用fp表示
3.局部自由度ft
概念:机构中不影响机构运动的自由度 表示:局部自由度以ft表示
综上所述，单环闭链机构自由度公式应为：
F

(5-7)
对于一般的没有公共约束的空间机构， λ =0，d=6。 在许多教科书中都是这样指出，平面机构
及球面机构都有 3 个公共约束， λ =3，是三阶机构 d=3 。并解释说，由于平面机构中所有转动
副轴线相互平行，所有构件都受到数量相等和性质相同的约束，都失去两个转动和一个移动运
动，构件只能在与轴线垂直的平面内作三自由度的运动，即沿平面内相互垂直的两方向的移动
1
··
论自由度与输入的关系。 关于自由度公式的发展，俄罗斯人有自己的看法。认为平面机构的自由度公式是切贝契夫
(Чебышев)[24,25]于1869年首先提出的；空间机构的自由度公式是马雷舍夫（Maлышев）提出的 [24,25]。1953年阿尔托波列夫斯基(Apтоболевский)在他的书中就提出应考虑机构的过约束修正自 由度公式 [26]。俄罗斯人的追求值得尊敬。
由度。最简单的例子就是门扇上的两个合页（转动副）。从运动学上说，一个合页就决定了门
的转动运动，另一个合页则没有起到对运动的任何约束作用，这即是过约束。上述前3种自由度 的计算公式共同存在一个问题是没有考虑过约束的情况，后两种企图考虑过约束，但人们也不
3
··
知道如何考虑。本书将在下节应用螺旋理论来考虑过约束情况，介绍普遍适用的自由度计算的 方法。
若在三维空间中有n个完全不受约束的物体，任选其中的一个为固定参照物，由于每个物体 相对参照物都有 6 个自由度，则系统中的 n 个物体相对选 定的参照物共有 6(n-1) 个自由度。若所有的物体之间都用 运动副连接起来，设第 i 个运动副带来的约束为 ui，由于 运动副的类型不同此约束可以是 1 和 5 之间的任何数，如 果运动副数目为 g，则这时机构的自由度就是所有运动构 件总的自由度减去所有的约束数的总和，即

机构的3n个自由度，受到2PL+PH个约束，则
机构自由度 F 3n 2PL PH
例2-3 求铰链四杆机构的自由度。
解：n=3，PL=4，PH=0
铰
F＝3×3－2×4－0＝1
链 四
（当构件1为原动件时，机构有确定的相对运
杆 机
动。给出一个参变量1，构件 2、3便有一个
构
相应位置）
例2-4 求三杆机构的自由度。
第二章 机构的结构分析
§2-1 机构结构分析的内容和目的 §2-2 机构的组成 §2-3 机构运动简图 §2-4 机构具有确定运动的条件 §2-5 机构自由度的计算 §2-6 计算机构自由度的应注意事项 §2-7 平面机构组成原理、结构分类及结构分析
返回
第二节 机构运动简图及其绘制
一、平面机构运动简图
• 视频
运动链成为机构的条件
Fa = 3×2 - 2×3 = 0 Fb运= 3动×链3的- 2自×由5度= -F1= ?
F 0 运动链运不动能链的运运动动，情不况成如为何机? 构
F = 3×4 - 2×5 = 2 1 个原动件
F > 0，但原动件数目小 于自由度数目，运动链 运动不确定，不能成为 机构。
F = 3×4 - 2×5 = 2 1 个原动件
F > 0，但原动件数目小 于自由度数目，运动链 运动不确定，不能成为 机构。
F = 3×3 - 2×4 = 1 2 个原动件
F > 0，但原动件数目大 于自由度数目，运动链 被破坏，不能成为机构。
一、机构自由度计算公式
设机构有N个构件，N-1=n个活动构件，用PL个低副，PH个高副连接后，
用简单的线条和符号来表示构件和运动副，并按比例 定出各运动副的位置。这种说明机构各构件间相对运动关 系的简单图形称为机构运动简图。

第5章空间机构自由度分析的约束螺旋求解法对机构最基本的认识是要知道它的自由度，机构的自由度计算原本是一个简单的问题，用传统的Kutzbach-Grübler公式[1-3]就可以获得正确的结果，而且仅仅基于算术运算。

这个最基本的问题几乎在所有的教科书上都有论述。

这里为什么还要论及呢？在机构学的发展历程中，发现了不少的机构不符合上述公式[4-5]。

这种情况长期来倒还能容忍，到底当时该公式对于绝大多数机构还是适用的，特别是适用于众多的平面机构。

但是在近十年来当空间机构研究迅速发展时，问题变得突出起来，传统的大家熟悉的这个公式常常算不出正确的结果，特别是在新世纪开始前后的这十年间，国际机构学界开展了少自由度并联机器人新机构的研究，这个不为人们重视的自由度计算却经常让人们迷惑，用公式常常不能够得到正确的结果。

甚至到了新世纪的2002年，美国马里兰大学的Tsai教授在分析他发明一种3自由度并联机构时再次指出，如果用Kutzbach-Grübler公式计算该机构的自由度数将会得到错误的结果[6]。

这样，人们不得不采取其它麻烦的分析方法[7-11]，多花费了很多的时间。

究其原因，认识到这是由于在机构中存在过约束（overconstrained）的缘故，约束被重复计算了。

许多人不断寻找新的普遍适用的机构的自由度计算公式，仅举文献[12-13]。

人们提出过许多新概念，包括公共约束、虚约束等等。

文献[14,15]还建议自由度公式中应采用机构螺旋系的“阶”。

在这方面国内也有许多学者进行了有意义的研究，文献[16]以闭合约束数定义公共约束以确定阶，文献[17]以非线性代数方程组的相关性来判定机构的“秩”，然而他却是一个十分困难的求解问题。

考虑“过约束”去对Kutzbach-Grübler公式加以修正，关键是如何分析过约束，到这个新世纪开始，这个问题在国际上一直未能解决。

还有一些学者甚至还采取如李代数和群论[18-20]等现代数学来探讨，也取得了一些进展。

2.5.2空间机构的自由度计算同平面机构自由度计算公式推导过程一样，空间机构的自由度 = 所有活动构件自由度 - 所有运动副引入的约束数，其公式为:F=6n-5P5-4P4-3P3-2P2-P1式中：n为活动构件数； P1、P2、P3、P4、P5分别为1~5级运动副的个数。

(a) (b)图2.5.2-1图(a)所示为自动驾驶仪操纵装置内的空间四杆机构。

活塞2相对气缸运动后通过连杆3使摇杆4作定轴转动。

构件1、2组成圆柱副，构件2、3和构件4、1分别组成转动副，构件3、4组成球面副，其运动示意图如图(b)所示。

试计算该机构的自由度。

解： n=3， P5=2， P4=1， P3=1F=6n-5P5-4P4-3P3-2P2-P=6×3-5×2-4×1-3×1=1.图(a)所示为某飞机起落架的收放机构。

构件1为原动件，构件1、2和2、3分别组成3级球副，构件1、4和3、4分别组成5级移动副和转动副，其运动示意图如图(b)所示。

试计算该机构的自由度并判断其运动是否确定。

解： n=3， P5=2， P3=2F=6n-5P5-4P4-3P3-2P2-P=6×3-5×2-3×2=1.计算结果表明需要2个原动件机构的运动才能得以确定。

而实际上该机构在1个原动件的带动下运动就能确定了。

上述问题出现在何处？(a) (b)图2.5.2-2构件2的两端同构件1、3分别组成球副，这样使得构件2可以绕自身轴线转动，而这个转动（自由度）对整个机构的运动没有影响，对比平面凸轮机构中滚子的转动一样，称为局部自由度。

图2.5.2-3 对于局部自由度也有两种处理方法:①. 修正自由度计算公式：F=6n-5P5-4P4-3P3-2P2-P1-k 式中：k为局部自由度数。

这样例题2的机构的自由度应为：F=6n-5P5-4P4-3P3-2P2-P1-k=6×3-5×2-3×2-1=1具有确定的运动。

第一章 机构旳构成及其自由度旳计算
§1.1 机构旳构成 §1.2 机构运动简图 §1.3 机构具有拟定运动旳条件 §1.4 平面机构自由度旳计算 §1.5 平面机构旳构成原理和构造分析
本章旳主要内容
1、主要内容 • 机构旳构成及其具有拟定运动旳条件 • 机构运动简图及其绘制 • 机构旳构成原理和机构旳构造分类 2、要点 • 机构具有拟定运动旳条件和平面机构自由度旳
构造分类：杆组为几级？什么形式？
例如Ⅱ级组：二杆三副组
外接副：与杆组以外旳构件相连旳运动副 内接副：与杆组内部旳构件相连旳运动副
例如Ⅲ级组：三杆六副组 特点：其中一种构件上有三个内接副
举例 5
构造分析：
从远离原动件旳构件开始，尽量 拆成最低旳杆组，每拆完一种杆组， 确保剩余旳杆组自由度为零。对剩 余旳杆组再拆时，仍从最远端开始 拆，每拆一次杆组，均从最低档旳 杆组开始，无法拆时，再试拆高一 级旳杆组。
凸轮机构:
举例 6
小结：掌握机构自由度旳计算措施； 机构具有拟定运动旳条件； 基本杆组拆分旳原则及措施。
局部运动并不影响整个机构中其他构件旳 运动
• 虚约束：机构中某些运动副或某些运动
副与构件旳组合所形成旳约束与其他约束 反复而不再起作用
举例 4
F 3n 2 pl ph 35260 3
F 3n 2 pl ph 33231 2
F 3n 2 pl ph 34260 0
虚约束注意事项
• 两个构件上参加接触旳运动副表面 称运动副元素，运动副旳元素是点、 线、面。
运动副分类： 空间和平面运动副
平面运动副
空间运动副
平面运动副：两构件相对运动为平面运动 旳运动副
低副：面接触旳运动副（回转副、移动副）

2.5.2空间机构的自由度计算同平面机构自由度计算公式推导过程一样，空间机构的自由度 = 所有活动构件自由度 - 所有运动副引入的约束数，其公式为:F=6n-5P5-4P4-3P3-2P2-P1式中：n为活动构件数； P1、P2、P3、P4、P5分别为1~5级运动副的个数。

(a) (b)图2.5.2-1图(a)所示为自动驾驶仪操纵装置内的空间四杆机构。

活塞2相对气缸运动后通过连杆3使摇杆4作定轴转动。

构件1、2组成圆柱副，构件2、3和构件4、1分别组成转动副，构件3、4组成球面副，其运动示意图如图(b)所示。

试计算该机构的自由度。

解： n=3， P5=2， P4=1， P3=1F=6n-5P5-4P4-3P3-2P2-P=6×3-5×2-4×1-3×1=1.图(a)所示为某飞机起落架的收放机构。

构件1为原动件，构件1、2和2、3分别组成3级球副，构件1、4和3、4分别组成5级移动副和转动副，其运动示意图如图(b)所示。

试计算该机构的自由度并判断其运动是否确定。

解： n=3， P5=2， P3=2F=6n-5P5-4P4-3P3-2P2-P=6×3-5×2-3×2=1.计算结果表明需要2个原动件机构的运动才能得以确定。

而实际上该机构在1个原动件的带动下运动就能确定了。

上述问题出现在何处？(a) (b)图2.5.2-2构件2的两端同构件1、3分别组成球副，这样使得构件2可以绕自身轴线转动，而这个转动（自由度）对整个机构的运动没有影响，对比平面凸轮机构中滚子的转动一样，称为局部自由度。

图2.5.2-3 对于局部自由度也有两种处理方法:①. 修正自由度计算公式：F=6n-5P5-4P4-3P3-2P2-P1-k 式中：k为局部自由度数。

这样例题2的机构的自由度应为：F=6n-5P5-4P4-3P3-2P2-P1-k=6×3-5×2-3×2-1=1具有确定的运动。

自由度数
机械系统中的自由度数等于系统 中独立构件的数目乘以每个构件 的自由度。
自由度在机械系统中的作用
确定机械系统的运动状态
自由度数决定了机械系统的运动状态，即系统能够完成的运动类型和数量。
判断机构的运动性质
通过计算自由度，可以判断机构是否具有确定的运动性质，即是否能够实现预 定的运动轨迹。
计算自由度的方法
详细描述
在机械设计阶段，通过绘制机构运动简图可以初步评估 机构的运动性能和自由度，为后续的设计优化提供依据 。在机构分析阶段，机构运动简图可用于研究机构的运 动规律、动态特性和稳定性等。在机械制造阶段，机构 运动简图可以用于指导生产装配和调试，确保机构的正 常运转。此外，机构运动简图还可以用于教学和培训， 帮助学生和工程师更好地理解机构的运动原理和工作方 式。
机械原理在工程实践中具有广泛 的应用价值，对于推动机械工程 领域的发展和技术进步具有重要
意义。
机械原理的发展历程
古代机械原理
古代人类在制造工具和机械时就开始积累机械知识，如轮子、杠杆、斜面等简单机械的发 明和应用。
工业革命时期的机械原理
随着工业革命的兴起，人们对机械系统的需求不断增加，促进了机械原理的发展。蒸汽机 、内燃机等复杂机械系统的出现和应用推动了机械工程领域的进步。
若要增加机构的自由度，可以通过增加活动构件数、减少低 副数或减少高副数来实现。
05 空间机构的自由度计算
空间机构自由度的计算公式
自由度的定义
自由度是指机构在空间中独立运动的 数量，用于描述机构在空间中的运动 状态。
计算公式的应用
通过将机构的构件数、运动副数和局 部自由度代入公式，即可求出机构的 自由度。
计算每个独立构件的自由度

自由度计算公式
自由度计算公式：1、自由度：机构的具有确定运动所必需要的独立运动参数为机构自由度。

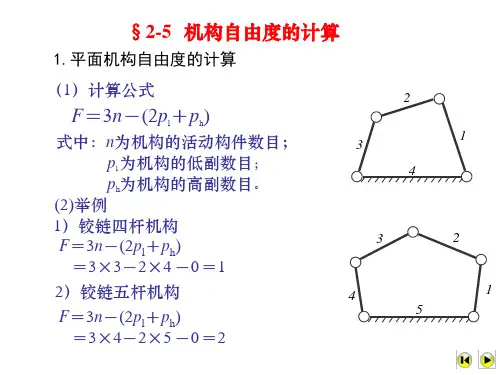
2、自由度计算公式：F=3n-2pl-2phn：活动构件数pl：低副数ph：高副数3、机构具有运动的条件：自由度=原动件数。

机构运动离不开自由度，自由度，分为平面机构自由度和空间机构自由度！
自由度：统计学术语：自由度(degree of freedom, df)指的是计算某一统计量时，取值不受限制的变量个数。

通常df=n-k。

其中n为样本数量，k为被限制的条件数或变量个数，或计算某一统计量时用到其它独立统计量的个数。

自由度通常用于抽样分布中。

物理学术语：自由度是指物理学当中描述一个物理状态，独立对物理状态结果产生影响的变量的数量。

如运动自由度是确定一个系统在空间中的位置所需要的最小坐标数。

例如火车车厢沿铁轨的运动，只需从某一起点站沿铁轨量出路程，就可完全确定车厢所在的位置，即其位置用一个量就可确定，我们说火车车厢的运动有一个自由度；汽车能在地面上到处运动，自由程度比火车大些，需要用两个量（例如直角坐标x,y）才能确定其位置，我们说汽车的运动有两个自由度；飞机能在空中完全自由地运动，需要用三个量（例如直角坐标x,y,z）才能确定其位置，我们说飞机在空中的运动有三个自由度。

所谓自由度数就是确定物体在空间的位置所需独立坐标的数目。