揭阳市2016届高中三年级学业水平考试(文数)

揭阳市2013—2014学年度高中三年级学业水平考试文综地理一、选择题：每小题列出的四个选项中，只有一项符合题目要求。

本大题共35小题，每小题4分，满分140分。

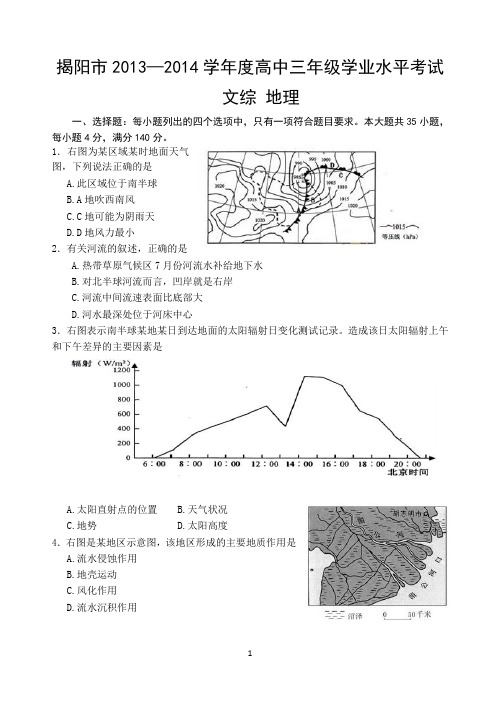
1．右图为某区域某时地面天气图，下列说法正确的是A.此区域位于南半球B.A地吹西南风C.C地可能为阴雨天D.D地风力最小2．有关河流的叙述，正确的是A.热带草原气候区7月份河流水补给地下水B.对北半球河流而言，凹岸就是右岸C.河流中间流速表面比底部大D.河水最深处位于河床中心3．右图表示南半球某地某日到达地面的太阳辐射日变化测试记录。

造成该日太阳辐射上午和下午差异的主要因素是A.太阳直射点的位置B.天气状况C.地势D.太阳高度4．右图是某地区示意图，该地区形成的主要地质作用是A.流水侵蚀作用B.地壳运动C.风化作用D.流水沉积作用下图为某一科考路线图，读图回答5—6题。

5．考察人员发现①地为热带雨林景观，与该景观 形成无关．．的是 A .终年受赤道低气压带控制 B .受来自海洋的东南信风影响 C .沿岸暖流的增温增湿作用 D .地形抬升作用，多地形雨6．考察人员经过③附近海区时，发现渔业资源丰富， 最有可能与下列哪一因素相关A.暖流经过B.寒暖流交汇C.有上升流D.陆地径流汇入 下表为“我国某地区的各类用地比重（%）”，根据表格回答7—8题。

7．20年间，有关该地区的可能变化是A.生态退耕导致耕地比重下降B.毁林开荒严重导致林地草地比重下降C.工业发展促进城镇化D.围湖造田导致水域比重下降 8．这种变化对地理环境带来的影响是A.水土流失减轻B.荒漠化加剧C.蒸发加强，降水增多D.雨季城镇内涝时有发生下图为我国某城市制造业空间集聚与扩散演变示意图（注：同心圆代表距市中心的距离），读图回答9—10题。

9．该市1996～2010年制造业空间变化的特点是①制造业集聚中心且逐步从城市中心区向郊区扩散 ②在城区周边形成多个集聚区 ③集聚中心并呈现出沿高速公路向外扩展的趋势 ④制造业重心有向北迁移的趋势 A.①②④ B.①②③ C.②③④ D.①②③④10．制造业空间集聚与扩散会影响城市土地利用的空间结构，以下因素对城市土地利用的空间结构有影响的是：①历史因素②土地价格③交通条件④生活习惯A.①②③B.②③④C.②③④D.①②③④11．下图表示我国部分省级行政区域2000-2010年间迁移人口比重，迁移人口以青壮年为主。

揭阳市2016－2017学年度高中二年级学业水平考试数学（文科）（测试时间120分钟，满分150分）注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.答题前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，写在本试卷上无效.3.回答第Ⅱ卷时，将答案写在答题卡上，答在本试卷上无效.4.考试结束，将本试卷和答题卡一并交回.第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知i 是虚数单位，若复数))((R a i a i ∈+-的实部与虚部相等，则=a （A ）2- （B ）1- （C ）1 （D ）2 （2）若集合{}0,1,2A =，{}24,B x x x N =≤∈，则AB =（A ）{}20≤≤x x （B ）{}22≤≤-x x （C ）{0,1,2} （D ）{1,2} （3）已知直线a ，b 分别在两个不同的平面α，β内.则“直线a 和直线b 没有公共点”是“平面α和平面β平行”的 （A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件（D ）既不充分也不必要条件（4）若()1sin 3πα-=，且2παπ≤≤，则sin 2α的值为（A ） （B ） （C （D （5）在区间[]1,4-上随机选取一个数，则1≤x 的概率为 （A ）23（B ）15 （C ）52 （D ）14图2俯视图侧视图主视图（6）已知抛物线2y x =的焦点是椭圆22213x y a +=的一个焦点，则椭圆的离心率为（A（B （C ）14 （D ）17（7）以下函数，在区间[3,5]内存在零点的是（A ）3()35f x x x =--+ （B ）()24x f x =-（C ）()2ln(2)3f x x x =-- （D ）1()2f x x=-+（8）已知(2,1),(1,1)a b ==，a 与b 的夹角为θ，则cos θ=（A（B（C（D （9）在图1的程序框图中，若输入的值为2，则输出的y 值为（A ）0 （B ）12 （C ）1- （D ）32-（10）某几何体的三视图如图2所示，则该几何体的侧面积是（A ）76（B ）70 （C ）64 （D ）62 （11）设2()3,()ln(3)x f x e g x x =-=+，则不等式(())(())11f g x g f x -≤的解集为（A ）[5,1]- （B ）(3,1]- （C ）[1,5]- （D ）(3,5]- (12) 已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且00x <，则a 的取值范围为（A ）∞（-,-2） （B ）1∞（-,-)（C ）(1,+)∞ （D ）(2,)+∞第Ⅱ卷本卷包括必考题和选考题两部分．第(13)题~第(21)题为必考题，每个试题考生都必须做答．第(22)题~第(24)题为选考题，考生根据要求做答． 二、填空题(本大题共4小题，每小题5分，共20分，请把正确的答案填写在答题卡相应的横线上．（13）函数()cos f x x x =+的最小正周期为 ．DC 1B 1CBA （14）已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-3322y x y x x y ，则y x -2的最小值为 .（15）已知直线l ：0x y a -+=，点()2,0A -，()2,0B . 若直线l 上存在点P 满足AP BP ⊥， 则实数a 的取值范围为 .（16）在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知2,b =3B π=，且△ABC的面积S =a c += .三、解答题：本大题必做题5小题，选做题2小题，共70分.解答应写出文字说明，证明过程或演算步骤．（17）（本小题满分12分）已知等差数列{}n a 满足141,4a a ==；数列{}n b 满足12b a =，25b a =，数列{}n n b a -为等比数列．(Ⅰ)求数列{}n a 和{}n b 的通项公式； (Ⅱ)求数列{}n b 的前n 项和n S ． （18）（本小题满分12分）某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成，现采用分层抽样的方法抽取5人，组成一个体验小组去市场体验“共享单车”的使用.问：（Ⅰ）应从该兴趣小组中抽取高一级和高二级的学生各多少人；（Ⅱ）已知该地区有X ,Y 两种型号的“共享单车”，在市场体验中，该体验小组的高二级学生都租X 型车，高一级学生都租Y 型车.如果从组内随机抽取2人，求抽取的2人中至少有1人在市场体验过程中租X 型车的概率. （19）（本小题满分12分）如图3，已知四棱锥11A CBB C -的底面为矩形，D 为1AC 的中点，AC ⊥平面BCC 1B 1． （Ⅰ）证明：AB//平面CDB 1; （Ⅱ）若AC=BC=1，BB 1（1）求BD 的长；（2）求三棱锥C-DB 1C 1的体积. 图3 （20）（本小题满分12分）已知过点(0,1)A 的动直线l 与圆C ：224230x y x y +---=交于M ，N 两点. （Ⅰ）设线段MN 的中点为P ，求点P 的轨迹方程; （Ⅱ）若2OM ON ⋅=-,求直线l 的方程. （21）（本小题满分12分）已知函数()ln f x x x =. （Ⅰ）求函数()f x 的极值；（Ⅱ）若对任意1,x e e ⎡⎤∈⎢⎥⎣⎦，都有()213022f x x ax +++≤成立，求实数a 的取值范围．请考生在(22)、(23)两题中任选一题作答，如果多做，则按所做的第一题记分. （22）（本小题满分10分）选修4-4：坐标系与参数方程将圆221x y +=上每一点的纵坐标不变，横坐标变为原的14，得曲线C . （Ⅰ）写出C 的参数方程；（Ⅱ）设直线l ：410x y ++=与C 的交点为P 1，P 2，以坐标原点为极点，轴正半轴为极轴建立极坐标系，求过线段P 1 P 2的中点且与l 垂直的直线的极坐标方程. （23）（本小题满分10分）选修4-5：不等式选讲设函数()|2|||f x x x a =-+-. （Ⅰ）若2a =-，解不等式5)(≥x f ；（Ⅱ）如果当x R ∈时，()3f x a ≥-，求a 的取值范围．揭阳市2016－2017学年度高中二年级学业水平考试数学(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数．一、选择题：（10）依题意知，该几何体是底面为直角梯形的直棱柱，故其侧面积为42+44+245=64⨯⨯⨯⨯.（11）(())(())11f g x g f x -≤即22(3)3211450x x x x +--≤⇒+-≤51x ⇒-≤≤，注意到30x +>，即3x >-，故31x -<≤.（12）当0a =时，函数2()31f x x =-+有两个零点，不符合题意，故0a ≠，2'()363(2)f x ax x x ax =-=-，令'()0f x =得0x =或2x a=，由题意知，0a >，且2()0f a>，解得2a >．二、填空题：2x y +=有公共点时，的取值范围，数形结合易得a -≤≤.（16）由余弦定理得2222cos 4b a c ac B =+-=，即224a c ac +-=，1sin 24S ac B ac ===得4ac =，故2()164a c a c +=⇒+= 三、解答题：（17）解：（Ⅰ）由数列{}n a 是等差数列且141,4a a ==∴公差4113a a d -==， ------------------------------------------------------------------------------1分∴1(1)n a a n d n =+-=，------------------------------------------------------------------------------3分∵12b a ==2，25b a ==5，∴11221,3,b a b a -=-= ∴数列{}n n b a -的公比22113b a q b a -==-，-----------------------------------------------------------5分∴1111()3n n n n b a b a q ---=-=，∴13n n b n -=+；-------------------------------------------------------------------------------------------7分(Ⅱ)由13n n b n -=+得21(12)(1333)n n S n -=++++++++--------------------------------------------------------9分(1)31231n n n +-=+- 3(1)12n n n ++-=------------------------------------------------------------------------------------ 12分（18）解：（Ⅰ）依题意知，应从该兴趣小组中抽取的高一学生人数为56=29+6⨯，------2EABCB 1C 1D分高二学生的人数为59=39+6⨯； -------------------------------------------------------------------4分（Ⅱ）解法1：记抽取的2名高一学生为12,a a ，3名高二的学生为123,,b b b ，------------5分则从体验小组5人中任取2人的所有可能为：12111213(,),(,),(,),(,)a a a b a b a b ，(a 2,b 1), (a 2,b 2),(a 2,b 3), (b 1,b 2), (b 1,b 3), (b 2,b 3)，共10种可能； ----------------------------------------------------------8分 其中至少有1人在市场体验过程中租X 型车的有：111213(,),(,),(,)a b a b a b ，212223121323(,),(,),(,),(,),(,),(,)a b a b a b b b b b b b 共9种，------------------------------------------10分故所求的概率910P =.-----------------------------------------------------------------------------------------12分【解法2：记抽取的2名高一学生为12,a a ，3名高二的学生为123,,b b b ，------------------------5分则从体验小组5人中任取2人的所有可能为：12111213(,),(,),(,),(,)a a a b a b a b ，212223121323(,),(,),(,),(,),(,),(,)a b a b a b b b b b b b 共10种可能；--------------------------------------8分其中所抽的2人都不租X 型车的有：12(,)a a 一种，-------------------------------------------------9分 故所求的概率1911010P =-=.---------------------------------------------------------------------------12分（19）解：（Ⅰ）证明：连结1BC 交1B C 于E ，连结DE ， ------------------------------------------1分∵D 、E 分别为1AC 和1BC 的中点，∴DE//AB,---------------------------------- --------------------2分 又∵DE ⊂平面1CDB ,AB ⊄平面1CDB ,∴AB//平面CDB 1;---------------------------------------------4分（Ⅱ）（1）∵AC ⊥平面BCC 1B 1，BC ⊂平面11BCC B ， ∴BC AC ⊥, 又∵1BC CC ⊥,1ACCC C =，∴BC ⊥平面1ACC ， ∵CD ⊂平面1ACC ,∴BC CD ⊥,----------------------------------------------------------------------------------------------------6分在Rt BCD ∆,∵BC=1，1112CD AC ===, ∴BD =; ----------------------------------------------------------------------------------------------------8分【注：以上加灰色底纹的条件不写不扣分！】 （2）解法1：∵BC ⊥平面1ACC ，BC//B 1C 1∴11B C ⊥平面1CC A ,-----------------------------------------------------------------------------------------10分∴111111113C DB C B CDC CDC V V S B C --∆==⋅111134=⨯⨯=.---------------------------------12分 【解法2：取1CC 中点F,连结DF ，∵DF 为△1ACC 的中位线，∴DF//AC,-------------------------------------------------------------------9分 ∵AC ⊥平面11CBB C ，从而可得DF ⊥平面11CBB C ,----------------------------------------------10分∴11111113C DB CD CB C CB C V V S DF--∆==⋅1111322=⨯⨯=.--------------------------------12分（20）解法（Ⅰ）将224230x y x y +---=化为标准方程得222(2)(1)x y -+-=,----------------------------------------------------------------------------1分可知圆心C 的坐标为(2,1),半径r =设点P的坐标为(,)x y ,则(2,1),(,1)CP x y AP x y =--=-,---------------------------------------2分依题意知CP AP ⊥,∴0CP AP ⋅=(2)(1)(1)0x x y y ⇒-+--=整理得222210x y x y +--+=, ------------------------------------------------------------------------4分∵点A 在圆C 内部, ∴直线l 始终与圆C 相交, ∴点P的轨迹方程为222210x y x y +--+=.----------------------------------------------------------6分（Ⅱ）设1122(,),(,)M x y N x y ,若直线l 与x 轴垂直,则l 的方程为0x =,代入224230x y x y +---= 得2230y y --=,解得1y =-或3y =, 不妨设121,3y y =-=,则3OM ON ⋅=-,不符合题设,------------------------------------------------7分 设直线l 的斜率为k ,则l 的方程为1y kx =+,由224230,1.x y x y y kx ⎧+---=⎨=+⎩消去y 得22(1)440k x x +--=, --------------------------------8分216(2)0k ∆=+>,则12122244,11x x x x k k+==-++,------------------------------------------------------------------------9分由2OM ON ⋅=-得212121212(1)()12x x y y k x x k x x +=++++=-, ∴22244(1)1211kk k k-+++=-++2410k k ⇒-+=, 解得2k =±,------ ---------------------------------------------------------------------------------------11分∴当2O M O N ⋅=-时,直线l 的方程为(21y x =+或(21y x =+.--------------12分（21）解：（Ⅰ）函数()f x 的定义域为(0,)+∞，∵()ln 1f x x '=+，令'()0f x =得1x e=，-------------------------------------------------------------2分 当10x e <<时'()0f x <，当1x e>时，'()0f x >， ∴函数()f x 在1(0,)e上单调递减，在1(,)e+∞上单调递增，----------------------------------------4分∴函数()f x 无极大值， 当1x e =时，函数()f x 在(0,)+∞有极小值，11()()f x f e e==-极小，--------------------------5分（Ⅱ）当1,x e e ⎡⎤∈⎢⎥⎣⎦时，由()213022f x x ax +++≤，得3ln 22x a x x ≤---，--------------6分记()3ln 22x g x x x =---，1,x e e ⎡⎤∈⎢⎥⎣⎦， 则()()()2231113222x x g x x x x +-'=--+=-， 当∈x 1,1e ⎛⎫ ⎪⎝⎭时，得'()0g x >，当∈x ()1,e 时， '()0g x < ∴()g x 在1,1e ⎛⎫⎪⎝⎭上单调递增，在()1,e 上单调递减，---------------------------------------------------9分 又113122e g e e ⎛⎫=-- ⎪⎝⎭，()3122e g e e=---， ∵012)()1(<-+=-e e e g e g ，∴()1g g e e ⎛⎫< ⎪⎝⎭，-------------------------------------------------10分故()g x 在1,e e ⎡⎤⎢⎥⎣⎦上的最小值为1g e ⎛⎫ ⎪⎝⎭，故只需1a g e ⎛⎫≤ ⎪⎝⎭，即实数a 的取值范围是13,122e e ⎛⎤-∞-- ⎥⎝⎦．------------------------------------------------------------12分 选做题：（22）解：（Ⅰ）由坐标变换公式1',4'.x x y y ⎧=⎪⎨⎪=⎩ 得4','x x y y ==-------------------------------------2分代入221x y +=中得2216''1x y +=，--------------------------------------------------------------------3分故曲线C 的参数方程为1cos ,4sin .x y θθ⎧=⎪⎨⎪=⎩(θ为参数）；----------------------------------------------------5分 （Ⅱ）由题知，121(,0),(0,1)4P P --，--------------------------------------------------------------------6分故线段P 1 P 2中点11(,)82M --，---------------------------------------------------------------------------7分∵直线l 的斜率4k =-∴线段P 1 P 2的中垂线斜率为14， 故线段P 1 P 2的中垂线的方程为111()248y x +=+------------------------------------------------------8分即832150x y --=，将cos ,sin x y ρθρθ==代入得其极坐标方程为8cos 32sin 150ρθρθ--=----------------------------------------------------------10分（23）解：(Ⅰ)当a ＝－2时，f ()＝|－2|＋|＋2|，①当2x ≤-时，原不等式化为：25,x -≥解得52x ≤-，从而52x ≤-；-------------------------1分②当22x -<≤时，原不等式化为：45≥，无解；---------------------------------------------------2分③当2x >时，原不等式化为：25,x ≥解得52x ≥，从而52x ≥；----------------------------------3分综上得不等式的解集为⎭⎬⎫⎩⎨⎧≥-≤2525x x x 或.----------------------------------------------------------------5分 (Ⅱ)当x R ∈时，|2||||x x a x x a a -+-≥---= ---------------------------------------7分所以当x R ∈时，()3f x a ≥-等价于|2|3a a -≥------（*）当2a ≥时，（*）等价于23,a a -≥-解得52a ≥，从而52a ≥；----------------------------------8分当2a <时，（*）等价于23,a a -≥-无解；------------------------------------------------------------9分故所求a 的取值范围为5[,+2∞）. --------------------------------------------------------------------------10分。

绝密★启用前揭阳市2016-2017学年度高中三年级学业水平考试数学(理科)本试卷共4页，满分150分．考试用时120分钟．注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效.3. 回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效.4. 考试结束，将本试题和答题卡一并交回.第Ⅰ卷一、选择题：共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．（1）已知集合{}3,2,1,0,1,2A =---，{}23B x x =≤，则AB =（A ）{}0,2 （B ）{}1,0,1- （C ）{}3,2,1,0,1,2--- （D ）[]0,2（2）复数z 满足(1＋i)z ＝i ＋2，则z 的虚部为（A ）32（B ）12（C ）12-（D ）12i -（3）已知等差数列{}n a 的前n 项和为n S ，且322315S S -=,则数列{}n a 的公差为（A ）3（B ）4（C ）5 （D ）6（4）设D 为△ABC 所在平面内一点，且3BC BD =,则AD =（A ）2133AB AC + （B ）1233AB AC + （C ）4133AB AC + （D ）2533AB AC + （5）若空间四条直线a 、b 、c 、d ，两个平面α、β，满足b a ⊥，d c ⊥，α⊥a ，α⊥c ，则（A ）α//b （B ）b c ⊥（C ）d b //（D ）b 与d 是异面直线（6）若命题：“20,20x R ax ax ∃∈-->”为假命题，则a 的取值范围是（A ）(,8][0,)-∞-+∞ （B ）(8,0)-（C ）(,0]-∞（D ）[8,0]-（7）函数],[|,|sin ππ-∈+=x x x y 的大致图象是（A ） （B ） （C ） （D ）（8）已知0a >且1a ≠，函数()13log ,0,0x x x f x a b x >⎧⎪=⎨⎪+≤⎩满足()02f =，()13f -=，则()()3f f -=（A ）3-（B ）2-（C ）3（D ）2（9）阅读如图1所示的程序框图，运行相应程序，输出的结果是 （A ）1234 （B ）2017 （C ）2258 （D ）722（10）六个学习小组依次编号为1、2、3、4、5、6，每组3人，现需从中任选3人组成一个新的学习小组，则3人来自不同学习小组的概率为（A ）5204（B ）4568（C ）1568（D ）568（11）直线:42l x y +=与圆22:1C x y +=交于A 、B 两点，O 为坐标原点，若直线OA 、OB 的倾斜角分别为α、β，则cos cos αβ+= 图1 （A ）1817 （B ）1217- （C ）417-（D ）417（12）已知,a b R ∈、且2222290ab a b ++-=，若M 为22a b +的最小值，则约束条件⎩⎨⎧≤+≤+.2||||,322M y x M y x 所确定的平面区域内整点（横坐标纵坐标均为整数的点）的个数为 （A ）29（B ）25（C ）18 （D ）16第Ⅱ卷本卷包括必考题和选考题两部分．第(13)题~第(21)题为必考题，每个试题考生都必须做答．第(22)题~第(23)题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分，共20分，请把正确的答案填写在答题卡相应的横线上．（13）在8)1(xx -的展开式中，常数项是 ．（14）设椭圆22221(0)x y a b a b+=>>的两焦点与短轴一端点组成一正三角形三个顶点，若焦点到椭圆上点的最大距离为,a b 为实半轴长和 虚半轴长，焦点在y 轴上的双曲线标准方程为 . （15）一几何体的三视图如图2示，则该几何体的体积为 . （16）已知正项数列{}n a 的首项11a =，且对一切的正整数n ，均有:211(1)(1)0n n n n n n a na n a a na +++-++-=，则数 图2列{}n a 的通项公式n a = .三、解答题：解答应写出文字说明，证明过程或演算步骤.（17）（本小题满分12分）在△ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，=1b ，且2c o s 20C a c --=．(Ⅰ)求角B 的大小；(Ⅱ)求△ABC 外接圆的圆心到AC 边的距离． （18）（本小题满分12分）如图3，在四棱锥ABCD P -中，AD O ∈，AD ∥BC ，AB ⊥AD ，AO=AB=BC=1，3=PC ．(Ⅰ)证明：平面POC ⊥平面P AD ；(Ⅱ）若AD=2，P A=PD ，求CD 与平面P AB 所成角的余弦值． 图3（19）（本小题满分12分）某商场举行促销活动，有两个摸奖箱，A 箱内有一个“1”号球、两个“2”号球、三个“3”号球、四个无号球，B 箱内有五个“1”号球、五个“2”号球，每次摸奖后放回．消费额满100元有一次A 箱内摸奖机会，消费额满300元有一次B 箱内摸奖机会，摸得有数字的球则中奖，“1”号球奖50元、“2”号球奖20元、“3”号球奖5元，摸得无号球则没有奖金． （Ⅰ）经统计，消费额X 服从正态分布)625,150(N ，某天有1000位顾客，请估计消费额X（单位：元）在区间（100，150]内并中奖的人数；附：若),(~2σμN X ，则6826.0)(=+<<-σμσμX P ，9544.0)22(=+<<-σμσμX P ．（Ⅱ）某三位顾客各有一次A 箱内摸奖机会，求其中中奖人数ξ的分布列；（Ⅲ）某顾客消费额为308元，有两种摸奖方法，方法一：三次A 箱内摸奖机会；方法二：一次B 箱内摸奖机会．请问：这位顾客选哪一种方法所得奖金的期望值较大． （20）(本小题满分12分)在平面直角坐标系xOy 中，已知点A （-1, 0）、B （1, 0）、C （0, -1），N 为y 轴上的点，MN 垂直于y 轴，且点M 满足AM BM ON CM ⋅=⋅（O 为坐标原点），点M 的轨迹为曲线T ．(Ⅰ)求曲线T 的方程；(Ⅱ)设点P （P 不在y 轴上）是曲线T 上任意一点，曲线T 在点P 处的切线l 与直线54y =-交于点Q ，试探究以PQ 为直径的圆是否过一定点？若过定点，求出该定点的坐标，若不过定点，说明理由．（21）（本小题满分12分）设a >0，已知函数)ln()(a x x x f +-=(x >0)．(Ⅰ)讨论函数)(x f 的单调性；(Ⅱ)试判断函数)(x f 在(0,)+∞上是否有两个零点，并说明理由．请考生在第（22）、（23）题中任选一题作答，如果多做，则按所做的第一个题目计分． （22）（本小题满分10分）选修4-4：坐标系与参数方程已知直线l 的参数方程为⎩⎨⎧+=+-=ααsin 1cos 1t y t x （t 为参数）．以O 为极点，x 轴的非负半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos +=θρρ．(Ⅰ)写出直线l 经过的定点的直角坐标，并求曲线C 的普通方程； (Ⅱ)若4πα=，求直线l 的极坐标方程，以及直线l 与曲线C 的交点的极坐标．（23）（本小题满分10分）选修4-5：不等式选讲设函数|2||1|)(--+=x m x x f ． (Ⅰ)若1m =，求函数)(x f 的值域； (Ⅱ)若1m =-，求不等式x x f 3)(>的解集．B ,y 1)x揭阳市2016-2017学年度高中三年级学业水平考试数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数．一、选择题：解析：（9） 输出结果为：2921211122221121-+++++=+=-（10）31363318()4568C C P C ==； （11）设1122(,),(,)A x y B x y ，由三角函数的定义得：12cos cos x x αβ+=+，由2242,1.x y x y +=⎧⎨+=⎩消去y 得：2174x x --则12417x x +=，即4cos cos 17αβ+=.（12）由2222290ab a b ++-=结合222aba b ≤+得22223()93a b a b +≥⇒+≥（当且仅当a b =时等号成立）故3M =,故约束条件确定的平面区域如右图阴影所示，在 区域内，由2,2x y =±=±围成的矩形区域（含边界）整点 有25个，加上圆2223x y +=与坐标轴的交点4个，共29个.二、填空题：解析：（15）==522=30222V V V V =+⨯⨯⨯长方体长方体长方体.（16）由211(1)(1)0n n n n n n a na n a a na +++-++-=1(1)(1)(1)0n n n n n a a na a +⇒++-+=，1(1)[(1)]0n n n a n a na +⇒++-=11n n a na n +⇒=+，则1212112112n n n n a a a n n a a a n n -----⋅=⋅-，1n a n⇒=. 三、解答题： （17）解：（Ⅰ）由2cos 20C a c --=，=1b 结合余弦定理得：22120a c a c a+---=，-------------------------------------------------------------------------------2分221a c ac ⇒+-=-，----------------------------------------------------------------------------------3分则2222211cos 222a cb ac B ac ac +-+-===-，-----------------------------------------------------5分∵0B π<< ∴23B π=.---------------------------------------------------------------------------7分(Ⅱ) 设△ABC 外接圆的半径为R ，由正弦定理知122sin sin 3b R B π===-------------------------------------------------------------------9分故R =,-------------------------------------------------------------------------------------------10分 则△ABC 外接圆的圆心到AC 边的距离6d ==.---------------------------------------------------------------12分（18）解：（Ⅰ）在四边形OABC 中，∵AO //BC ，AO =BC ，AB ⊥AD ，∴四边形OABC 是正方形，得OC ⊥AD ，-----------------------2分在△POC 中，∵222PC OC PO =+，∴OC ⊥PO ，-------4分又O AD PO = ，∴OC ⊥平面P AD ，又⊂OC 平面POC ，∴平面POC ⊥平面P AD ；-------------6分 （Ⅱ）解法1：由O 是AD 中点，P A=PD ，得PO ⊥AD ； 以O 为原点，如图建立空间直角坐标系O -xyz ， ---------- 7分 得)0,1,0(-A ，)0,1,1(-B ，)2,0,0(P ，)0,0,1(C ，)0,1,0(D ， 得)0,1,1(-=CD ，)2,1,0(--=PA ，)0,0,1(=AB ，E设),,(z y x m =是平面P AB 的一个法向量，则⎪⎩⎪⎨⎧⊥⊥m PA m ，得⎪⎩⎪⎨⎧==⋅=--=⋅002x m z y m ，取z =1，得)1,2,0(-=m，----------------------------------------------------------------------------------10分 设CD 与平面P AB 所成角为θ，则|||||,cos |sin m CD m⋅=><=θ33322=⋅=， ∴36cos =θ，即CD 与平面PAB------------------------------12分【解法2：连结OB ，∵OD//BC ，且OD=BC ∴BCDO 为平行四边形，∴OB//CD, ----------------------------7分由（Ⅰ）知OC ⊥平面P AD ，∴AB ⊥平面P AD ，∵AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ，----------------------------------------------------8分过点O 作OE ⊥PA 于E ，连结BE ，则OE ⊥平面PAB ， ∴∠OBE 为CD 与平面PAB 所成的角，----------------------10分 在Rt △OEB中，∵PO AO OE PA ⋅==,OB =,∴cos BEOBE OB∠=== 即CD 与平面P AB--------------------------------------------------12分】（19）解：（Ⅰ）依题意得150=μ，6252=σ，得25=σ，σμ2100-=， ------------ 1分消费额X 在区间（100，150]内的顾客有一次A 箱内摸奖机会，中奖率为0.6，--------- 2分人数约为)2(1000μσμ≤<-⨯X P 29544.01000⨯==477人，------------------------3分其中中奖的人数约为477×0.6=286人； -------------------------------------------------------- 4分（Ⅱ）三位顾客每人一次A 箱内摸奖中奖率都为0.6，三人中中奖人数ξ服从二项分布)6.0,3(B ，k k kC k P -⋅==334.06.0)(ξ，（k=0, 1, 2, 3） ----------------------------------------------------6分故ξ的分布列为-----------8分（Ⅲ）A 箱摸一次所得奖金的期望值为50×0.1+20×0.2+5×0.3=10.5，-------------------------9分B箱摸一次所得奖金的期望值为50×0.5+20×0.5=35，---------------------------------------10分方法一所得奖金的期望值为3×10.5=31.5，方法二所得奖金的期望值为35， 所以这位顾客选方法二所得奖金的期望值较大．-----------------------------------------------12分 （20）解：（Ⅰ）设点(,)M x y ，依题意知(0,)N y ，∵(1,),(1,),(0,),(,1)AM x y BM x y ON y CM x y =+=-==+，---------------------------2分 由AM BM ON CM ⋅=⋅得221(1)x y y y -+=+，即21y x =-， ∴所求曲线T 的方程为21y x =-------------------- 4（Ⅱ）解法1：设000(,)(0)P x y x ≠， 由21y x =-得'2y x =则00'|2l x x k y x ===---------------------------5分 ∴直线l 的方程为：0002()y y x x x -=-令54y =-得200418x x x -=，即点Q 的坐标为20041(8x x -设(,)G x y 是以PQ 为直径的圆上任意一点，则由得以PQ 为直径的圆的方程为：20000415()()()()084x x x x y y y x ---+-+=------①-----------8分在①中，令001,0x y =±=得35(1)()()084x x y y ++++=，------------------------②35(1)()()084x x y y --++=， -----------------------------------------------------------③由②③联立解得0,3.4x y =⎧⎪⎨=-⎪⎩或 0,1.2x y =⎧⎪⎨=-⎪⎩--------------------------------------------------------------10分将30,4x y ==-代入①式，左边=20041335()()8444x y -+---+0011022y y =-==右边， 即以PQ 为直径的圆过点3(0,)4-，--------------------------------------------------------------------11分将10,2x y ==-代入①式，左边≠右边，∴以PQ 为直径的圆恒过点，该定点的坐标为3(0,)4---------------------------------------------12分【解法2：设000(,)(0)P x y x ≠，由21y x =-得'2y x =则00'|2l x x k y x === -----------------------------------------------------------------------------------------5分∴直线l 的方程为：0002()y y x x x -=-令54y =-得200418x x x -=，即点Q 的坐标为200415(,)84x x ---------------------------------------------6分设(,)G x y 是以PQ 为直径的圆上任意一点，则由0PG QG ⋅=，得以PQ 为直径的圆的方程为：20000415()()()()08x x x x y y y x ---+-+=------①------------8分假设以PQ 为直径的圆过定点),(b a ， 则0)45)(()8121)((0000=+-++--b y b x x a x a ， 0)45)(1(81823212000202=++-+-+-+b x b x a ax x a ， )45)(1()45(81823212000202++++--+-+b b x b x a ax x a 0)45)(1()43(81)8123(20002=++++----b b x b x x a a ，令43,0-==b a ，上式恒成立， ∴以PQ 为直径的圆恒过定点，该点的坐标为3(0,)4-----------------------------------------------12分】【解法3：设000(,)(0)P x y x ≠，由21y x =-得'2y x =则00'|2l x x k y x ===------------------------------------------------------------------------------------------5分∴直线l 的方程为：0002()y y x x x -=-令54y =-得200418x x x -=，即点Q 的坐标为200415(,)84x x --------------------------------------------6分假设以PQ 为直径的圆恒过定点H ，则根据对称性，点H 必在y 轴上，设(0,)H t ， 则由0PH QH ⋅=得20000415()()084x x t y t x -⋅+-+=------① --------------------------------------8分001355()()02844y t t y t +++-+=，031()()042t t y ++-=， ∴34t =-，即以PQ 为直径的圆恒过定点，该点的坐标为3(0,)4---------------------------12分】（21）解：（Ⅰ）ax xx f +-=121)('，----------------------------------------------------------------1分0)2(220)('22>+-+⇔>+⇔>a x a x x a x x f ，0)2(20)('22<+-+⇔<a x a x x f ，设22)2(2)(a x a x x g +-+=，则)1(16a -=∆， ①当1≥a 时，0≤∆，0)(≥x g ，即0)('≥x f ， ∴)(x f 在),0(∞+上单调递增；-----------------------------------------------------------------3分②当10<<a 时，0>∆， 由0)(=x g 得a a aa x ---=---=122214241，aa x -+-=1222，-----------------------------------------------------------------------------4分可知210x x <<，由)(x g 的图象得：)(x f 在)122,0(a a ---和),122(∞+-+-a a 上单调递增；--------------------5分)(x f 在,122(a a ---)122a a -+-上单调递减． ---------------------------------6分（Ⅱ）解法1：函数)(x f 在(0,)+∞上不存在两个零点 ----------------------------------------------7分假设函数)(x f 有两个零点，由（Ⅰ）知，10<<a ， 因为0ln )0(>-=a f ，则0)(2<x f ，即)ln(22a x x +<， 由0)('2=x f 知222x a x =+，所以）（222ln x x <，设t x =2，则)2l n(t t <（＊）， -----------------------------------------------------------------9分 由)4,1(1222∈-+-=a a x ，得)2,1(∈t ，设)2ln()(t t t h -=，得011)('>-=t t h ， -------------------------------------------------10分所以)(t h 在)2,1(递增，得02ln 1)1()(>-=>h t h ，即)2ln(t t >，这与（＊）式矛盾， ---------------------------------------------------------------------------------11分所以上假设不成立，即函数)(x f 没有两个零点． ------------------------------------------12分【解法2：函数)(x f 在(0,)+∞上不存在两个零点； -------------------------------------------------7分由（Ⅰ）知当1≥a 时，函数)(x f 在),0(∞+上单调递增，∴函数)(x f 在),0(∞+上至多有一个零点；-----------------------------------------------------8分当10<<a 时，∵0ln )0(>-=a f ，由（Ⅰ）知当2x x =时，()f x 有极小值，22()=()ln()f x f x x a =+极小11)]=-，---------------------9分1,t =则12t <<，()ln(2)f x t t =-极小，设)2ln()(t t t h -=，得011)('>-=t t h ，------------------------------------------------------10分∴)(t h 在)2,1(单调递增，得02ln 1)1()(>-=>h t h ，即()0f x >极小，可知当10<<a 时，函数)(x f 在(0,)+∞不存在零点；综上可得函数)(x f 在(0,)+∞上不存在两个零点.-------------------- -----------------------12分】选做题：（22）解：（Ⅰ）直线l 经过定点)1,1(-，-----------------------------------------------------------------2分由2cos +=θρρ得22)2cos (+=θρρ，得曲线C 的普通方程为222)2(+=+x y x ，化简得442+=x y ；---5分（Ⅱ）若4πα=，得⎪⎪⎩⎪⎪⎨⎧+=+-=t y t x 221221，的普通方程为2+=x y ，----------------------------------6分则直线l 的极坐标方程为2cos sin +=θρθρ，------------------------------------------------8分联立曲线C ：2cos +=θρρ．得1sin =θ，取2πθ=，得2=ρ，所以直线l 与曲线C 的交点为)2,2(π．------------10分（23）解：（Ⅰ）当1m =时，|2||1|)(--+=x x x f -------------------------------------------------1分∵3|)2()1(|||2||1||=--+≤--+x x x x ，-------------------------------------------------3分 3|2||1|3≤--+≤-∴x x ，函数)(x f 的值域为]3,3[-；------------------------------ 5分（Ⅱ）当m =－1时，不等式x x f 3)(>即x x x 3|2||1|>-++，------------------------------- -6分①当1-<x 时，得x x x 321>+---，解得51<x ，1-<∴x ； --------------------- 7分②当21<≤-x 时，得x x x 321>+-+，解得1<x ，11<≤-∴x ； --------------- 8分③当2≥x 时，得x x x 321>-++，解得1-<x ，所以无解； ------------------------9分综上所述，原不等式的解集为)1,(-∞． -----------------------------------------------------10分。

揭阳市2015-2016学年度高中三年级学业水平考试数学(理科)本试卷共4页，21小题，满分150分．考试用时120分钟．注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效。

3.答案第Ⅱ卷时，将答案写在答题卡上，答在本试卷上无效。

4.考试结束后，将本试题和答题卡一并交回。

第Ⅰ卷一、选择题：共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{}{}2=1,2,1,0,1,2M x x N >=--，则MN =（A ） {}0 （B ） {}2 （C ）{}2,1,1,2-- （D ）{}2,2- 2.复数112i i i -+的实部与虚部的和为 （A ）12- （B ） 1 （C ）12 （D ）323.在等差数列{}n a 中，已知35710132,9a a a a a +=++=，则此数列的公差为 （A ）13 （B ）3 （C ）12 （D ）164.如果双曲线经过点p ，且它的一条渐近线方程为y x =，那么该双曲线的方程式（A ）22312y x -= （B ） 22122x y -= （C ）22136x y -= （D ）22122y x -= 5.利用计算机在区间（0,1）上产生随机数a,则不等式ln(31)0a -<成立的概率是 （A ）13 （B ）23 （C ）12 （D ）146.设,a b 是两个非零向量，则“222()a b a b +=+”是 “a b ⊥”的 （A ）充分不必要条件 （B ）必要不充分条件（C ）充要条件 （D ）既不充分又不必要条件7.已知奇函数()y f x =的图像关于直线2x =对称，且()3f m =， 则(4)f m -的值为（A ）3 （B ）0 （C ）-3 （D ）138.函数24()cos cos f x x x =-的最大值和最小正周期分别为 （A ）1,4π （B ）1,42π （C ）1,2π （D ）1,22π9.某人以15万元买了一辆汽车，此汽车将以每年20%的速度 折旧，图1是描述汽车价值变化的算法流程图，则当n=4时， 最后输出的S 的值为 （A ）9.6 （B ）7.68 （C ）6.144 （D ）4.915210.如图2，网格纸上小正方形是边长为1，粗线画出的是一正方 体被截去一部分后所得几何体的三视图，则该几何体的表面积为 （A ）54 （B ）162（C ）54+（D ）162+11.已知直线0x y a -+=与圆心为C 的圆2270x y ++-+=相交于A ，B 两点，且4AC BC ⋅=，则实数a 的值为（A （B（C （D ）12.若函数32()21f x x ax =-++存在唯一的零点，则实数a 的取值范围为 （A ）[0,)+∞ （B ）[0,3] （C ）(3,0]- （D ）(3,)-+∞第Ⅱ卷本卷包括必答题和选考题两部分，第13题～第21题为必答题，每个试题考生都必须作答，第22题～第24题为选考题，考生根据要求作答。

揭阳市2016－2017学年度高中二年级学业水平考试
数学（文科）
（测试时间120分钟，满分150分）
注意事项：
1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分
.答题前，考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改
动，用橡皮擦干净后，再选涂其他答案标号，写在本试卷上无效.
3.回答第Ⅱ卷时，将答案写在答题卡上，答在本试卷上无效
.4.考试结束，将本试卷和答题卡一并交回.
第Ⅰ卷
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）已知
i 是虚数单位，若复数))((R a i a i 的实部与虚部相等，则a （A ）
2（B ）1（C ）1 （D ）2 （2）若集合0,1,2A
，24,B x x x N ，则A B = （A ）20x x （B ）22x x （C ）{0,1,2}
（D ）{1,2} （3）已知直线a ，b 分别在两个不同的平面
α，β内.则“直线a 和直线b 没有公共点”是“平面α和平面β平行”的
（A ）充分不必要条件
（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件
（4）若1
sin 3
，且2，则sin 2的值为（A ）42
9（B ）229（C ）229（D ）
429（5）在区间
1,4上随机选取一个数x ，则1x 的概率为（A ）2
3（B ）15（C ）52
（D ）1
4。

揭阳市2015—2016学年度高中三年级学业水平考试理科综合本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分300分。

考试时间150分钟。

注意事项：1．本次考试选择题用答题卡作答，非选择题用答题卷作答。

答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卷上。

用黑色字迹的钢笔或签字笔在答题卡上填写自己的姓名和考生号，用2B型铅笔把答题卡上考生号、科目对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁，考试结束后，将答题卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 F 19 Na 23 Al 27Si 28 S 32 Cl 35.5 Ca 40 Fe 56 Cu 64第Ⅰ卷一．选择题：本题共有13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列关于细胞的分子组成和基本结构的阐述，正确的是A．含有C、H、O、N元素的有机物属于生物大分子B．线粒体、核糖体、染色体、叶绿体等结构中都含有DNAC．分泌蛋白合成越旺盛的细胞，其高尔基体膜更新的速度越快D．动物激素是基因表达的直接产物，可调节生命活动2．研究发现，线粒体促凋亡蛋白Smac是细胞中一个促进细胞凋亡的关键蛋白，正常细胞中Smac存在于线粒体中，当线粒体收到释放这种蛋白质的信号时，就会将它释放到线粒体外，然后Smac与凋亡抑制蛋白（IAPs）反应，促进细胞凋亡。

下列有关叙述正确的是A．细胞凋亡时具有水分减少、代谢减慢、所有酶的活性下降等特征B．Smac从线粒体释放时不需消耗能量C．癌细胞的无限增殖，可能与细胞内IAPs基因过度表达和Smac从线粒体中释放受阻有关D．Smac与IAPs在细胞凋亡中的作用相同揭阳市2015—2016学年度高中三年级学业水平考试理科综合试题第1页（共14页）3．下列关于生物体生命活动调节的叙述，正确的是：A．在苹果成熟的过程中，果实内乙烯量比生长素量的比值会下降B．寒冷时，体内甲状腺激素分泌增加，促甲状腺激素也随之增加C．体液免疫中的抗体可以抑制病原体的繁殖，也可抑制其对人体细胞的黏附D．当人吃过咸食物后, 大脑皮层渗透压调节中枢兴奋，产生渴觉，引起喝水行为4．DNA分子经过诱变，某位点上的一个正常碱基（设为X）变成了尿嘧啶，该DNA连续复制两次，得到的4个DNA分子相应位点上的碱基对分别为U—A、A—T、G—C、C—G，可推测“X”可能是A．胸腺嘧啶B．胞嘧啶C．腺嘌呤D．胸腺嘧啶或腺嘌呤5．研究表明，青少年型糖尿病是由免疫系统错误地破坏胰岛B细胞而导致。

绝密★启用前揭阳市2013-2014学年度高中三年级学业水平考试数学(文科)本试卷共4页，21小题，满分150分．考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须填写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回． 参考公式：棱锥的体积公式：13V Sh =．其中S 表示棱锥的底面积，h 表示棱锥的高． 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 在复平面内，复数(1)i i -对应的点位于A.第一象限B. 第二象限C.第三象限D. 第四象限 2. 已知集合{|lg(3)},{|2}A x y x B x x ==+=≥，则下列结论正确的是 A.3A -∈ B.3B ∉ C.AB B = D.A B B =3. “φπ=”是“函数sin(2)y x φ=+为奇函数的” A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件4. 向量(1,2),(3,4),BA BC =-=则AC =A.(4,2)B.(4,2)--C.(2,6)D.(4,2)- 5. 某商场有四类食品,食品类别和种数见右表:现从中抽取一个容量为20的样本 进行食品安全检测.若采用分层抽样的 方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是A. 7B. 6C. 5D. 4图（1）侧视图正视图俯视图6. 方程125x x -+=的解所在的区间A ．（0，1）B ．（1，2）C ．（2，3）D ．（3，4）7. 若双曲线22221x y a b-=A.2±B. C.12±D. 8. 已知x 、y 满足约束条件5315,10,5 3.x y x y x y +≤⎧⎪-+≥⎨⎪-≤⎩则35z x y =+的最小值为A.17B. -11C.11D.-17 9. 图（1）中的网格纸是边长为1的小正方形，在其上用粗线画 出了一四棱锥的三视图，则该四棱锥的体积为.A.4B.8C.16D.2010. 已知函数221,(0)()3,(0)ax x x f x ax x ⎧++≤=⎨->⎩有3个零点，则实数a 的取值范围是A. 1a <B.0a >C.1a ≥D. 01a <<二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分． （一）必做题（11－13题） 11. 计算：33log 18log 2-= ．12. 图（2）是甲、乙两人在5次综合测评中的成绩的茎叶图，其中一个数字被污损；则甲的平均成绩超过乙的平均成绩的概率为 ． 13．对于正整数n ，若(,,)n p q p q p q N*=≥∈,当p q -最小时，则称pq 为n 的“最佳分解”，规定()qf n p=．关于()f n 有下列四个判断：①(4)1f =；②1(13)13f =；③3(24)8f =；④1(2013)2013f =．其中正确的序号是 ． （二）选做题（14—15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在极坐标中，已知点P 为方程()cos sin 2ρθθ-=所表示的曲线上一动点，4,3Q π⎛⎫⎪⎝⎭，则PQ 的最小值为 ．图（4）六级五级四级三级二级一级空气质量级别2天数6481015．(几何证明选讲选做题) 如图（3），已知AB 是圆O 的直径，C 是AB 延长线上一点，CD 切圆O 于D ，CD=4，AB=3BC ，则 圆O 的半径长是 ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）设数列{}n a 是公比为正数的等比数列，12a =，3212a a -=． （1）求数列{}n a 的通项公式；（2）设数列{}n b 是首项为1，公差为2的等差数列，求数列{}n n a b +的前n 项和n S ． 17. （本小题满分12分）根据空气质量指数AQI （为整数）的不同，可将空气质量分级如下表:某市2013年10月1日—10月30日，对空气质量指数AQI 进行监测,获得数据后得到如图（4）的条形图（1）估计该城市本月(按30天计)空气质量类别为中 度污染的概率；（2）在空气质量类别颜色为紫色和褐红色的数据中 任取2个,求至少有一个数据反映的空气质量类别颜色为褐 红色的概率.18．（本小题满分14分）在△ABC 中，角A 、B 、C 所对应的边为c b a ,, （1）若cos()2cos ,3A A π-= 求A 的值；（2）若1cos ,3A =且△ABC的面积2S =，求C sin 的值. 19．（本小题满分14分）50 51100101150151200300一级 二级 三级 四级 五级 优 良 轻度污染 中度污染 重度污染 严重污染图（6）yxBOEFD如图（5），已知,,A B C 为不在同一直线上的三点，且111////AA BB CC ，111AA BB CC ==.(1)求证:平面ABC //平面111A B C ；(2)若1AA ⊥平面ABC ，且14AC AA ==,3,5BC AB ==, 求证：A 1C 丄平面AB 1C 1(3)在（2）的条件下，设点P 为1CC 上的动点，求当1PA PB +取得最小值时PC 的长.20.（本小题满分14分）如图（6），已知(,0)F c 是椭圆2222:1(0)x yC ab a b +=>>的右焦点； 222:()F x c y a -+=与x 轴交于,D E 两点，其中E 是椭圆C 的左焦点.(1)求椭圆C 的离心率；(2)设F 与y 轴的正半轴的交点为B ，点A 是点D 关于y 轴的对称点，试判断直线AB 与F 的位置关系；(3)设直线BF 与F 交于另一点G，若BGD ∆的面积为C 的标准方程.21.（本小题满分14分）设函数1()n n f x axbx c +=++(0)x >，其中0a b +=，n 为正整数，a ，b ，c 均为常数，曲线()y f x =在(1,(1))f 处的切线方程为10x y +-=. （1）求a ，b ，c 的值； （2）求函数()f x 的最大值；（3）证明：对任意的(0,)x ∈+∞都有1()nf x e<.（e 为自然对数的底）揭阳市2013-2014学年度高中三年级学业水平考试数学（文科）参考答案及评分说明一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则． 二、对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数． 四、只给整数分数． 一．选择题CC A AB CBBCD解析：10.函数()f x 有3个零点，须满足0,20,012440.a a a a <⎧⎪⎪-<⇒<<⎨⎪->⎪⎩，故选D.二．填空题：11.2;12.45;13．①②；15. 3. 解析：12.设被污损的数字为x （x N ∈），则由甲的平均成绩超过乙的平均成绩得，88899291908383879990x ++++>+++++，解得08x ≤<，即当x 取0,1，……，7时符合题意，故所求的概率84105P == 三．解答题：16.解：（1）设数列{}n a 的公比为q ，由12a =，3212a a -=，得222120q q --=，即260q q --=．------------------------------------------------------------3分 解得3q =或2q =-，------------------------------------------------------------------------------------5分 ∵0q >∴2q =-不合舍去，∴123n n a -=⨯；---------------------------------------------------------6分（2）∵数列{}n b 是首项11,b =公差2d =的等差数列，∴n b =21n -，-------------------------------------------------------------------------------------------------8分 ∴n S 1212()()n n a a a b b b =+++++++2(31)(121)312n n n -+-=+-231n n =-+．--------------------------------------------------------12分17.解：（1）由条形统计图可知,空气质量类别为中度污染的天数为6, -----------------------------1分所以该城市本月内空气质量类别为中度污染的概率 61305P ==.----------------------------------4分 （2）由条形图知，空气质量类别颜色为紫色的数据有4个，分别设为a b c d 、、、，空气质量类别颜色为褐红色的数据有2个，分别设为e f 、.------------------------------------------------------6分设从以上6个数据任取2个，至少有一个数据反映的空气质量类别颜色为褐红色为事件A,则基本事件有：(,),(,),(,),(,),(,),(,)a b a c a d b c b d c d ，(,),(,),(,),(,),(,),(,)a e a f b e b f c e c f ，(,),(,),(,)d e d f e f 共15种可能，--------------------------------------------------------------------------8分A 包含的基本事件有：(,),(,),(,),(,),(,),(,)a e a f b e b f c e c f ，(,),(,),(,)d e d f e f 9种可能，-------------------------10分故所求的概率93()155P A ==.-------------------------------------------------------------------------------------------------12分 18.解：（1）由cos()2cos ,3A A π-=得cos cossin sin2cos ,33A A A ππ+=---------------------------------------------------------------------2分1cos 2cos ,22A A A ∴+=s i n 3c o sA A =,------------------------------------------------4分∴tan A =分 ∵0A π<< ∴3A π=；-------------------------------------------------------------------------------------7分（2）解法1：1cos ,3A = ∴02A π<<∴sin A =------------------------------------------------------------------------------8分由21sin 23S bc A ===得3b c =，----------------------------------------------------------10分由余弦定理得：22222222cos 928a b c bc A c c c c =+-=+-=，∴a =----------------12分由正弦定理得：sin sin a c A C =，即sin sin cA C=1sin3C∴==.------------------------------------------------------------------------------------------14分【解法2：1cos,3A =∴02Aπ<<∴sin3A=------------------------------------------------------------------------------8分由21sin2S bc A===得3b c=，----------------------------------------------------------10分由余弦定理得：22222222cos928a b c bc A c c c c=+-=+-=，∴a=----------------12分∵22222289a c c c c b+=+==，∴△ABC是Rt△，角B为直角，--------------------------------13分1sin3cCb∴==．---------------------------------------------------------------------------------------------14分】【:解法3：1cos,3A =∴02Aπ<<∴sin A=------------------------------------------------------------------------------8分由21sin23S bc A===得3b c=，----------------------------------------------------------10分由余弦定理得：22222222cos928a b c bc A c c c c=+-=+-=，∴a=----------------12分又21sin2S ab C==，得213s i n22c C⋅⋅⋅=，∴1sin3C=.-----------------------14分】【解法4：1cos,3A =∴02Aπ<<∴sin A=------------------------------------------------------------------------------8分由21sin23S bc A===得3b c=，----------------------------------------------------------10分由正弦定理得：sin sinb cB C=，则3sin sin sin[()]C B A Cπ==-+sin()A C=+，-------11分3sin sin()sin cos cos sinC A C A C A C=+=+,13sin cos sin33C C C=+,整理得cos C C =,代入22sin cos 1C C +=,得21sin 9C =，------------------------------13分 由c b <知02C π<<,1sin 3C ∴=.----------------------------------------------------------------------------------------------------14分】 19.（1）证明：∵11//AA CC 且11AA CC =∴四边形11ACC A 是平行四边形，-------------------------------------------------------------------------------1分 ∴//AC 11AC ,∵AC ⊄面111A B C ，11AC ⊂面111A B C∴//AC 平面111ABC ，-------------------------------------------------------------------------------------------3分 同理可得//BC 平面111ABC ,又ACCB C =,∴平面ABC //平面111ABC ----------------------------------------------------------------------------------------------------4分 (2)∵1AA ⊥平面ABC ，1AA ⊂平面11ACC A ∴平面11ACC A ⊥平面ABC ，-------------------5分 平面11ACC A 平面ABC =AC ，∵4AC =,3BC =,5AB = ∴222AC BC AB += ∴BC AC ⊥ ---------------------------6分∴BC ⊥平面11ACC A ,----------------------------------------------------------------------------------------7分 ∴1BC AC ⊥，∵11//BC B C ∴111B C AC ⊥ 又1AA AC ⊥,1AC AA =得11ACC A 为正方形，∴11AC AC ⊥---------------------------------------8分 又1111AC B C C =,∴A 1C 丄平面AB 1C 1----------------------------------------------------------------------------------------------9分 （3）将三棱柱ABC-A 1B 1C 1的侧面11ACC A 绕侧棱1CC 旋转到与侧面11BCC B 在同一平面内如右图示，连结1AB 交1CC 于点P ，则由平面几何的知识知，这时1PA PB +取得最小值，----------------------------------------------12分∵1//PC BB4PABA 1B 1C 13∴11167AC BB PC ACPC BB AB AB ⋅=⇒==.------------------------------------------------------------------14分 20.解：(1)∵圆F 过椭圆C 的左焦点，把(,0)c -代入圆F 的方程，得224c a =，故椭圆C 的离心率12c e a ==；---------------------------------------------------------------3分 (2) 在方程222()x c y a -+=中令0x =得2222y a c b =-=，可知点B 为椭圆的上顶点， 由(1)知，12c a =，故2,a c b ===，故B (0,，-------------------------------5分 在圆F 的方程中令y=0可得点D 坐标为(3,0)c ，则点A 为(3,0)c -，------------------------------6分于是可得直线AB 的斜率AB k ==，---------------------------------------------------------------7分 而直线FB 的斜率FB k ==，----------------------------------------------------------------------8分 ∵1AB FD k k ⋅=-, ∴直线AB 与F （3）∵DF 是△BDG ∴2BDG BFD S S ∆∆=|=∴22c =，从而得a 21解：（1）∵(1)f a b c c =++=由点(1,)c 在直线1x y +=上，可得11c +=，即0c =.----1分 ∵1'()(1)nn f x a n x bnx-=++，∴'(1)()f a b n a a =++=. -----------------------------------------2分又∵切线1x y +=的斜率为1-，∴1a =-，∴1a =-，1,0b c ==.-----------------------------------------------------------------------------------------3分 （2）由（1）知，1()n nf x x x +=-+，故1()(1)()1n n f x n x x n -'=+-+.------------------------------4分令()0f x '=，解得1n x n =+，即()f x '在(0,)+∞上有唯一零点01nx n =+. ---------------------------5分当01n x n <<+时，()0f x '>，故()f x 在(0,)1nn +上单调递增；------------------------------------6分当1n x n >+时，()0f x '<，故()f x 在(,)1nn +∞+单调递减.-------------------------------------------7分∴()f x 在(0,)+∞上的最大值max()f x =1()()(1)111(1)nn n n n n n f n n n n +=-=++++. -----------------8分 （3）证法1：要证对任意的(0,)x ∈+∞都有1()nf x<，只需证1()f x <，由（2）知在(0,)+∞上()f x 有最大值，max ()f x 分 即11()1n n n e +<+，即1ln 011n n n +<++，分 令,(01)1n t t n =<<+，则111t n =-+，①即ln t 分 令()ln 1,(01)g t t t t =-+<<，则1'()1g t t =-=分显然当01t <<时，'()0g t >，所以()g t 在(0,1)上单调递增， ∴()(1)0g t g <=，即对任意的01t <<②恒成立， ∴对任意的(0,)x ∈+∞都有1()nf x e<.------------------------------------------------------------------14分 【证法2：令1()ln 1+(0)t t t t ϕ=->，则22111()= (0)t t t t t tϕ-'=->.----------------------------------9分 当01x <<时，()0t ϕ'<，故()t ϕ在(0,1)上单调递减； 而当1x >时， ()0t ϕ'>，故()t ϕ在(1,)+∞上单调递增.∴()t ϕ在(0,)+∞上有最小值，min ()(1)0t ϕϕ==. -----------------------------------------------------10分 ∴()0(1)t t ϕ>>，即1l n 1(1)t t t>->.---------------------------------------------------------------------11分令11t n =+，得11ln 1n n n +>+，即11ln()lne n n n++>，--------------------------------------------------12分所以11()e n n n++>，即11(1)e n n n n n +<+.-----------------------------------------------------------------------13分 由（2）知，11()(1)en n n f x n n +≤<+，故所证不等式成立.---------------------------- ------------------14分】。

揭阳市2015—2016学年度高中三年级学业水平考试语文参考答案及评分标准 第1页 （共4页）揭阳市2015—2016学年度高中三年级学业水平考试语文参考答案及评分标准一、9分1．A(原文是“从历史上看，潮汕一直以‘国角尾省’自称——它所表现的不仅仅是地理位置的偏僻，更多的是基于在“居中自傲”的中原王朝，这样的称谓表明了潮汕文化一直处于中原主流文化的边缘和受排斥。

”选项少了“从历史上看”及“基于在‘居中自傲’的中原王朝”的时代背景，缺少这两个限制条件，“自古而今”绝对化了，表述有误。

)2．B(原文是“在他们看起来．．．．．．非常适合居住的南蛮之地——潮汕地区的海洋性气候十分适合人的居住”，非常合适居住是人们的看法，不等同于现实，另外“合适”也只是指潮汕地区的海洋气候十分适合人居住。

选项不符合原文意思。

)3．D(原文是“因而，我们可以看到，虽然如同中国其他乡村宗族一样，在建国之后由于强大的政治压力而使宗族活动暂时处于停滞状态，然而，在这个过程中，所谓社会主义主流意识形态的整合并没有动摇了宗族认同意识的基础。

”原文提及“没有动摇了宗族认同意识基础”的是“社会主义主流意识形态的整合”，此外，没有动摇“宗族认同意识的基础”并不能作为论断“宗族活动是暂时处于停滞状态”的理由；选项强加因果。

) 二、36分（一）19分4、A （应为“认可、认同”）5、C6、C （农夫被拘，皇帝查明缘由后，罢免宦官，赏赐农夫十匹帛，而非张建封求情）7、（1）宦官主持宫市，没有诏文验证，只要说是宫市，就没有人敢盘问，大致给的钱不抵原价的十分之一。

（“主”“谁何”“十不偿一”各1分，大意2分） （2）残余拖欠的赋税日积月累，肯定没有办法再收回的，即使免除，老百姓也没有什么好处。

（“逋” “蠲除”“无所”各1分，大意2分） （二）11分8、“清”既指环境的清，又指心境的清。

（2分）月透疏帘而入，如同邀来婆娑的月影；溪声传至耳边，如同被奇妙地纳入枕函之中，借清凉的月影、溪声写出了环境之清静；诗人注目于这些光景物态，于枕上感受月影、溪声，表现了清闲的心境。

揭阳市2015-2016学年度高中三年级学业水平考试数学（文科)本试卷共4页，满分150分．考试用时120分钟．注意事项：1.本试卷分第Ⅰ卷（选择题)和第Ⅱ卷(非选择题）两部分.答题前，考生务必将自己的姓名、准考证号填写在答题卡上.2。

回答第Ⅰ卷时,选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效。

3。

回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效。

4。

考试结束，将本试题和答题卡一并交回。

第Ⅰ卷一、选择题：共12小题，每小题5分，共60分．在每个小题给出的四个选项中,只有一项是符合题目要求的． 1．已知集合2{|20}A x xx =-≤，{0,1,2,3}B =，则AB =(A ） {12}， (B) {012}，，(C){1}（D ）{123}，，2．已知复数z 满足(21)2z i +=，则z = (A ）12i --（B ）12i -+ (C ）12i -- (D)12i - 3．已知向量(1,2),(1,1)a b =-=-，则()a b a -⋅=(A) 8 (B)5 (C) 4 （D) 4-4．若方程()20f x -=在区间(0,)+∞有解，则函数()y f x =的图象可能是5．在等差数列{}na 中，已知35710132,9,aa a a a +=++=则此数列的公差为(A) 31 (B)3 （C) 12（D) 166．利用计算机在区间 （0，1)上产生随机数a ，则不等式ln(31)0a -<成立的概率是 (A ） 12(B)23(C ） 31 （D)147．抛物线28y x =的焦点到双曲线2213y x -=的渐近线的距离是(A)错误!(B ）错误!（C ） 1（D ）38．函数22()cos ()cos ()44f x x x ππ=--+的最大值和最小正周期分别为 （A ）1,2π（B) 1,π （C)1,22π （D ）1,2π9．某人以15万元买了一辆汽车，此汽车将以每年20%的速度折旧，图1是描述汽车价值变化的算法流程图，则当4n =时,最后输出的S 为 （A)9.6 (B)7.68 （C)6.144 (D ）4.9152 10．已知棱长为2的正方体ABCD-A 1B 1C 1D 1的一个面A 1B 1C 1 D 1在一半球底面上，且A 、B 、C 、D 四个顶点都在此半球面上,则此半球的体积为(A ） （B)(C) （D ）11．已知抛物线C :28yx =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线i =1输入S =15否i =i +1开始结束输出Si >n ？S ＝S (1-20%)是图1PF 与C 的一个交点，若20FP FQ +=,则||QF =(A)3 (B ）4 (C)6 （D ）8 12．若关于x 的方程24sin sin 10x m x -+=在(0,)π内有两个不同的实数解，则实数m 的取值范围为（A) 4m >或4m <- （B)45m << （C ）48m << （D ）5m >或4m =第Ⅱ卷本卷包括必考题和选考题两部分．第13题第21题为必考题,每个试题考生都必须做答．第22题第24题为选考题,考生根据要求做答．二、填空题（本大题共4小题,每小题5分，共20分，请把正确的答案填写在答题卡相应的横线上． 13． 已知121(),(,1);4()log ,[1,).xx f x x x ⎧∈-∞⎪⎪=⎨⎪∈+∞⎪⎩，则((2))f f -= ．14．设变量x ，y 满足约束条件222y xx y x ≥⎧⎪+≤⎨⎪≥-⎩,则3z x y =-的最小值为 ．15．如图2,网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截 去部分的几何体的表面积为 ． 16．数列{}na 的通项公式(1)2cos()n n nan n π=-⋅+⋅，其前n 项和为n S ，则10S 等于 。

绝密★启用前揭阳市2013-2014学年度高中三年级学业水平考试数学(文科)本试卷共4页，21小题，满分150分.考试用时120分钟.注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须填写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.参考公式：棱锥的体积公式：V=-Sh•其中S表示棱锥的底面积，力表示棱锥的高.3一、选择题：本大题共10小题，每小题5分，满分50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在复平面内，复数z(z-l)对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限2.已知集合A = {x|y = lg(x+3)),B = {x|x>2},则下列结论正确的是A.-3e A C. AC\B = B D. A\JB = B3.“0 =兀”是“函数y = sin(2x + 0)为奇函数的”A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.向fiBA = (-l,2),BC = (3,4),则疋=A. (4,2)B. (-4,-2)C. (2,6)D. (-4,2).某商场有四类食品，食品类别和样本进行食品安全检测•若采用分层抽样的方法抽取样木，则抽取的植物油类与果蔬类食品种数Z和是A. 7B. 6C. 5D. 46.方程2t-1+x = 5的解所在的区间A. (0, 1)B.(1, 2)C.(2, 3)D.(3, 4)7.若双曲线二-・=i 的离心率为则其渐近线的斜率为 cT 少（二）选做题（14—15题,考生只能从中选做一题）14.（坐标系与参数方程选做题）在极坐标中，已知点P 为方程p （cos^-sin^） = 2所表示的曲线上一动点，Q 4,-,则|PQ|的最小值为 __________________\ 3丿15.（几何证明选讲选做题）如图（3）,已知AB 是圆0的肓径，C 是AB 延长线上一•点，CD 切圆0于D, CD 二4, AB=3BC,则圆0的半径长是 ______ .三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.A. ±2B. ±V2c.±l10.已知函数"0 =严+2兀+ 1,（*0）有3个零点，则实数d 的取值范围是 ax 一 3,（兀〉0）A. d v 1B. a >0C. a>\D. 0<a<l填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分.（一）必做题（11 一 13题）11. 计U ： log 318-log 3 2 =12. 图（2）是卬、乙两人在5次综合测评中的成绩的茎叶图，瓦中一个 数字被污损；则甲的平均成绩超过乙的平均成绩的概率为 ______ •9 8 83 3 72 1 0 913.对于正整数八若n- pq （p>q.p,qe N^），当p-q 最小时，则称为n 的“最佳分解”，规定/（町=2.关于/⑺）冇下列四个判断：①/（4） = 1；②/（⑶=2；③p 133/(24)=-；O④ 7(2013) =12013•其中正确的序号是 D16.（本小题满分12分）设数列｛©｝是公比为正数的等比数列，67, =2, a 3-a 2=12.（1） 求数列｛色｝的通项公式;（2） 设数列｛仇｝是首项为1,公差为2的等差数列，求数列｛色+如 的前n 项和S”. 17.（本小题满分12分）AQI （数值）on 5051J 1001013 150151 匚 200201匚 300>300空气质量级别 一级 一.级 三级 四级 五级 六级 空气质量类别 优 良 轻度污染 中度污染 重度污染 严重污染 空气质量类別颜色绿色黄色橙色红色紫色褐红色根据空气质量指数AQI （为整数）的不同，可将空气质量分级如下表:某市2013年10月1日一10月30日，对空气质量指数AQI 进行监测,获得数据后得火数到如图（4）的条形图（1） 估计该城市本月（按30天计）空气质量类别为中度污染的概率；（2） 在空气质量类别颜色为紫色和褐红色的数据中108 ------------------------------------空气质昴级别三级四级五级六级°任取2个,求至少有一个数据反映的空气质量类别颜色为褐图（4）红色的概率.18.（本小题满分14分）在AABC 中,角A 、B. C 所对应的边为a.b.c7T(1)若 cos( ----- A) = 2 cos A.求 A 的值；3B（2）若COSA = ?HAABC 的面积"屁，求sinC 的值.Bi求证：A】C丄平面ABC⑶在(2)的条件卜；设点P为CG上的动点，求当PA+PB］取得最小值时PC的长20.(本小题满分14分) x2 y2如图(6),已知F(c，O)是椭圆C: —+ ^ = 1(^>/?>0)的右焦点;cr tr□F:(X-C)2+/=672与x轴交于DE两点，其中E是椭IMIC的左焦点.⑴求椭圆C的离心率;(2)设口F与y轴的正半轴的交点为B，点A是点D关于y轴的对称点,试判断直线与□ F的位置关系；(3)设肓•线BF与口F交于另一点G ,若^BGD的而积为伍，求椭圆C的标准方程.21.(本小题满分14分)设函数/(x) = ax n^ + hx n + c(3： > 0),其中a + h = 0f n为正整数，a, b, c均为常数,曲线尸/(%)在(1J⑴)处的切线方程为兀+ y -1 = 0・(1)求b, c的值；(2)求函数/心)的最大值；(3)证明：对任意的xw(0,+2 )都有//(%) <丄.(£为自然对数的底)e揭阳市2013-2014学年度高中三年级学业水平考试数学(文科)参考答案及评分说明一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考杳内容比照评分标准制订和应的评分细则.二、对计算题当考牛的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，nJ视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分.三、解答右端所注分数，表示考牛正确做到这一步应得的累加分数.四、只给整数分数.一.选择题CC A AB CBBCDa <0,9解析:10.函数/(Q有3个零点，须满足彳——<0, nOvovl,故选D.2a4一牝>0.x ►y 图(6)二.填空题：11.2； 12.纟；13.①②;14. V6 ； 15. 3・5 -----解析：12.设被污损的数字为x (XG A^),则由甲的平均成绩超过乙的平均成绩得，88 + 89 + 92 + 91+90〉83 + 83 + 87 + 99 + 90 + 兀，解得05兀<8,即当x 取0,1,……8 47吋符合题意，故所求的概率P = - = -10 5三.解答题：16 .解：(1)设数列｛陽｝的公比为g ,由务=2, Oj-02 =12 ,得2g2_2g_]2 = 0,即q_ — q— 6 = 0. 3 分解得g = 3或g = —2 ,----- 5分・.・q > 0・・・q = -2不合舍去，・・・％ = 2 x 3心；----------------------------------------------------------------------------- 6分(2) •・•数列｛仇｝是首项$ =1,公差d = 2的等差数列，.・.仇=2n — 1, ----------------------------------------------------------------------------------------------------- 8分S” =(4 +---------- H Q“)+ (勺 +〃2 -亿)2(3" -1) 71(1 + 2/2-1) 1 , 2= ----------- 1 -------------- = 3—1+7?. ----------------------------------------------------- 3-1 2------------------ 12分17.解：(1)由条形统计图可知,空气质量类别为屮度污染的天数为6,-------------------------------------- 1分所以该城市木月内空气质暈类别为屮度污染的概率P = —= --------------------------------------------- 4 分30 5(2)由条形图知，空气质量类别颜色为紫色的数据有4个，分别设为弘b、c、d ,空气质罐类别颜色为褐红色的数据有2个，分别设为e、f . ------------------------------------------------------------------------- 6 分设从以上6个数据任取2个，至少有一个数据反映的空气质量类別颜色为褐红色为事件A,则基本事件有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(a, e), (a, /), (b, e)9 (b, .f), (c, e\ (c, f),A 包含的基本事件有：(&,e)9 (a, /), (b, e), (b, f\ (c, e\ (c, /), (d, e\ (〃, /),(匕 f) 9 种可能, 10分故所求的概率12分7T1& 解：(1)由 cos(A-y) = 2 COS A, cos A cos —+ sin Asin —= 2 cos A. 3 3--------------------------- 2分V3sin A = 3cos A tan A = V3IT 0 < A< 7T A =—3P(A)9 _3 15 _5'/. —cos A +22 cos 4,由余弦定理得：a 2 =b 2+c 2- 2/?ccos A = 9c 2 4- c 2 - 2c 2= 8c 2,12分•: a 2+c 2 =Sc 2+c 2 =9c 2 =b 2 f AAABC 是 RtZ\,角 B 为直角, ------------------------------------------ 13分 sin C =—=—. -----------------------------h 3----------------------------------------- 14分】【：解法 3： vcosA = -, /. 0 < A < — 3 2sin A - Vl - cos 2 A =310分由 余弦定 理得： a 1 =b~ ^-c 2 -2/?ccos A = 9c 2 +c 2 - 2c 2 =a = 2\/2c ---------------------- 12 分又 S=-^sinC = V2c 2 , 得L ・2 近c ・3c ・sWC = 4ic222III S"宀#csin 心爭c得b = 3c •小 sin A /. sinC =——产 2<214分【解法2： z 心，,.0<A 煜/. sin A = Vl-cos 2A =2V21 0由S"宀尹sirM 盲阮得X3c,10分sinC = -. --------------------------------- 14 分】31 71【解法 4： TCOS A = —, /• 0 < A < —32--------------------------------- 10分h r由止弦定理得： --- = ----- ,则 3sin C = sin B = sin [兀 一(A + C)] = sin(A + C),sin B sin C-------- 11分2V2 13sin C = sin(A + C) = sin A cos C + cos Asin C, 3sinC = ------ cos C +—sin C,3 3整理得cosC = 2V2sinC ，代入sin 2C + cos 2 C = l,得sin 2 C = -,9---------------------------------------- 13分7T由 c<b^0<C<-f2•小1sine =. ------------------------------------------------------------------------------------------------3-------------------------------------------- 14分】 19. (1)证明：・・・* //CC,且側=cc }・••四边形ACC/|是平行四边形,1分/.AC/ / A }C }, AC ex 而 A B 、G , AQ u 面人 BQ・・・AC//平面ABQ,sin A = A /I-COS 2A =2V2同理可得B C / /平面A d G,又A C n CB = C,・・・平而ABC//平面AEG------------------------- 4分⑵•・• A4］丄平面ABC , A4, u平面ACC^ .:平面ACC^丄平面ABC ,----------------------- 5分平面ACC.A, CI平面ABC二AC,v AC = 4f BC = 3f AB = 5 :. AC2 + BC2 = AB2 :. BC丄AC・・・BC丄平面ACC|A, -------------------------------------------------------- 7分・•・BC 1. A}C , •・・BC/ /BC・•・BC丄AC又A4,丄AC, AC = AA.得ACC/】为正方形，二4C1 AC, ----------------------------------------------------- 8分、G = G，又AC} n B・・・A】C丄平面AB I C l ---------------------------------------------------------------------------------------------------- ------------------ 9分(3)将三棱柱ABC-A.B.G的侧而ACC.A绕侧棱CC】旋转到与侧而BCC.B,在同一平而内如PC AC门门AC • BB、 16---- —=> rC = -------------------------------------------------------------------- L =—. BB X AB -------------------------------------------------------------------- A B 720.解：(1)・・・圆F过椭圆C的左焦点，把(-c,O)代入圆F的方程，得14c2 = a2,故椭圆C的离心率《 = — = —：a 2--------------------------------------------------------------------------------- 3分⑵ 在方程(x-c)2 + y2=a2中令兀=0得y2=a2-c2=h29可知点B为椭圆的上顶点,由⑴知，—=—,故a = 2c,b = yja2—c1 = V3c»故B (0, V3c),a 2-------------------------------------- 5分在圆F的方程中令y=0可得点D坐标为(3c,0),则点A为(-3c,0),-------------------------------------- 6分于是可得直线AB的斜率k AB =¥ =写'--------------------------------------------------------------------------------- 7分而直线FB的斜率k FR— --- = —>/3 ,-C丿•* 5 • kpD = -1，・•・直线AB与口F相切。