最新人教版2018-2019学年八年级数学上册：平方差公式-同步练习(2)及答案-精品试题

初中数学人教版八年级上册实用资料平方差公式和完全平方公式（习题）➢ 例题示范例1：计算：23(1)(1)2(1)a a a -+---+．【操作步骤】（1）观察结构划部分：23(1)(1)2(1)a a a -+---+① ②（2）有序操作依法则：辨识运算类型，依据对应的法则运算．第一部分：a -和a -符号相同，是公式里的“a ”，1和-1符号相反，是公式里的“b ”，可以用平方差公式；第二部分：可以用完全平方公式，利用口诀得出答案．（3）每步推进一点点．【过程书写】解：原式2223()12(21)a a a ⎡⎤=---++⎣⎦223(1)242a a a =----2233242a a a =----245a a =--➢ 巩固练习1. 下列多项式乘法中，不能用平方差公式计算的是（ ）A ．()()x y y x ---+B ．()()xy z xy z +-C ．(2)(2)a b a b --+D ．1122x y y x ⎛⎫⎛⎫--- ⎪⎪⎝⎭⎝⎭ 2. 下列各式一定成立的是（ ）A ．222(2)42x y x xy y -=-+B ．22()()a b b a -=-C ．2221124a b a ab b ⎛⎫-=++ ⎪⎝⎭ D ．222(2)4x y x y +=+ 3. 若2222(23)412x y x xy n y +=++，则n =__________．4. 若222()44ax y x xy y -=++，则a =________．5. 计算： ①112233m n n m ⎛⎫⎛⎫--- ⎪⎪⎝⎭⎝⎭； ②22()()()y x x y x y -++；③22(32)4x y y ---；④2()a b c +-；⑤296；⑥2112113111-⨯．6. 运用乘法公式计算：①2(2)(2)(2)x y x y x y -+-+；②22(1)2(24)a a a +--+；③(231)(231)x y x y +--+；④3()a b -；⑤222233m m⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭；⑥2210199-．➢ 思考小结1. 在利用平方差公式计算时要找准公式里面的a 和b ，我们把完全相同的“项”看作公式里的“_____”，只有符号不同的“项”看作公式里的“_____”，比如()()x y z x y z +---，_______是公式里的“a ”，_______是公式里的“b ”；同样在利用完全平方公式的时候，如果底数首项前面有负号，要把底数转为它的______去处理，比如22()(_______)a b --=2. 根据两大公式填空：+(_______)+(_______)b )22(2【参考答案】➢ 巩固练习1. C2. B3. ±34. -25. ①22149n m - ②44x y -+③2912x xy + ④222 222a ab b bc ac c ++--+ ⑤9 216 ⑥16. ①242xy y -- ②267a a -+-③224961x y y -+- ④322333a a b ab b -+- ⑤83m⑥400➢ 思考小结1. a ，b ，(x -z )，y ，相反数，a +b2. 2ab ，2ab ，4ab。

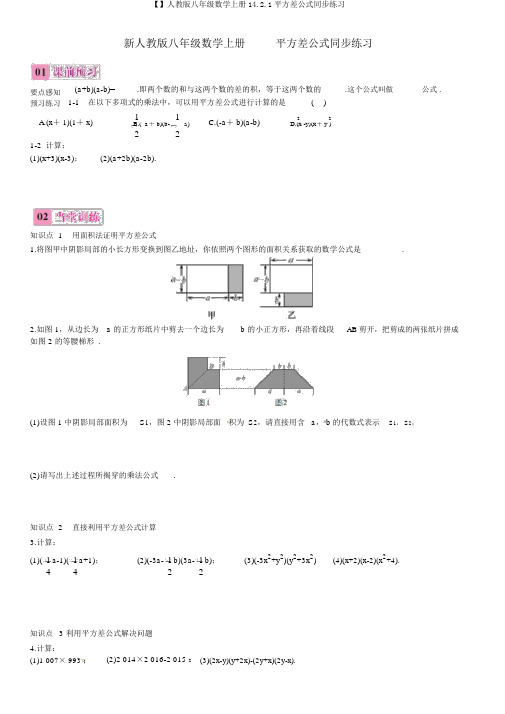
新人教版八年级数学上册平方差公式同步练习要点感知预习练习(a+b)(a-b)=_____.即两个数的和与这两个数的差的积，等于这两个数的1-1在以下多项式的乘法中，可以用平方差公式进行计算的是().这个公式叫做_____公式 .A.(x＋ 1)(1＋ x)11C.(-a＋ b)(a-b)22 B.( a＋ b)(b-a)D.(x -y)(x＋ y )221-2 计算：(1)(x+3)(x-3)；(2)(a+2b)(a-2b).知识点 1用面积法证明平方差公式1.将图甲中阴影局部的小长方形变换到图乙地址，你依照两个图形的面积关系获取的数学公式是.2.如图1，从边长为 a 的正方形纸片中剪去一个边长为 b 的小正方形，再沿着线段AB 剪开，把剪成的两张纸片拼成如图 2 的等腰梯形 .(1)设图 1 中阴影局部面积为S1，图 2 中阴影局部面积为S2，请直接用含a， b 的代数式表示S1， S2；(2)请写出上述过程所揭穿的乘法公式.知识点 2直接利用平方差公式计算3.计算：(1)(1a-1)(1a+1)；(2)(-3a-1b)(3a-1b)；(3)(-3x2+y2)(y2+3x2)(4)(x+2)(x-2)(x2+4).4422知识点 3 利用平方差公式解决问题4.计算：(1)1 007× 993 ；(2)2 014×2 016-2 015 2(3)(2x-y)(y+2x)-(2y+x)(2y-x).5.先化 ，再求 ：(a+b)(a-b)+a(2b-a) ，其中， b=2.6.以下各式中，能用平方差公式 算的是 ( )① (7ab-3b)(7ab+ 3b)；② 73×94 ；③ (-8+a)(a-8)；④ (-15-x)(x-15).A.①③B.②④C.③④D.①④7. 于任意正整数n ，能整除式子 (m+3)(m-3)-(m+2)(m-2) 的整数是 ( )8. 算 (x 2+ 1 )(x+ 1 )(x- 1 )的 果 ()4 224+ 1 4- 1 4-1 x 2+ 1 4- 1 x 2+ 116162 168 169. 两个正方形的 之和5， 之差 2 ，那么用 大的正方形的面 减去 小的正方形的面 ，差是 ____.10. (a ＋ b-3)2＋ (a-b ＋ 5)2＝ 0， a 2-b 2 =___.11. 算：(1)(2m+3n)(2m-3n) ；(2)(- 1x 2+2)(- 1x 2-2)；(3)(-x-y)(x-y)；2 2(4)(a+2b)(a-2b)- 1b(a-8b) ；(5)213 2-214× 212.212.(衡阳中考 )先化 ，再求 ：(1)(1+a)(1-a)+a(a-2)，其中 a= 1；(2)(a ＋ b)(a-b)＋ 2a 2，其中 a ＝1， b ＝ 2.213.解方程： (3x)2-(2x+1)(3x-2)=3(x+2)(x-2).挑 自我14. x ≠ 1， 算： (1+x)(1-x)=1-x 2， (1-x)(1+x+x 2 )=1-x 3 ，(1-x)(1+x+x 2+x 3)=1-x 4.2 n(1) 察以上各式并猜想： (1-x)(1+x+x +⋯ +x )=____.(n 正整数 )(2)依照你的猜想 算：① (1-2)(1+2+22+23+24+25)=___.23n② 2+2 +2 +⋯+2 =___(n 正整数 ). ③ (x-1) (x 99+x 98+x 97+⋯+x 2+x+1)=.(3)通 以上 律 你 行下面的研究：① (a-b)(a+b)=___.② (a-b)(a 2+ab+b 2)=___.3223③ (a-b)(a +a b+ab +b )=___.参照答案课前预习要点感知a2-b 2平方差平方差预习练习 1 -1 B1-2〔1〕原式=x2-9.(2)原式=a2-(2b)2=a2-4b2.当堂训练1.(a+b)· (a-b)=a2-b22.(1)S1＝ a2-b2， S2＝1(2b＋ 2a)(a-b)＝(a＋ b)(a-b).(2)(a ＋b)(a-b)＝ a2-b 2. 21 3.(1)原式 =16222444a -1.(2)原式 =-9a +14b.(3)原式 =y -9x.(4)原式 =x -16.4.(1)原式 =999 951.(2)原式 =-1.(3)原式 =5 x2-5y2.5.原式=2.课后作业7.D8.B9.1010.-1511.(1)原式=4m2-9n2.(2)原式=1x4-4.422.(4)原式21(3)原式 =y -x=a -ab.(5) 原式 =1.214.(1)1-x n+1(2 )① -63②2n+1-2③ x 100-1(3)① a2-b2② a3-b3③ a4-b4 12.(1)0.(2)1.13.x=-14.。

8年级上册数学人教版《14.2.1 平方差公式》课时练一、单选题1．运用乘法公式计算（4+x ）（x ﹣4）的结果是（ ）A ．x 2﹣16B ．x 2+16C ．16﹣x 2D ．﹣x 2﹣162．已知5a b -=，则2210a b b --的值为（ ）A ．5B ．10C ．15D ．253．下列各式不能用平方差公式计算的是（ ）A ．(23)(23)x y x y -++B ．(23)(32)x y y x --C ．(23)(32)x y y x -+--D ．(23)(23)x y x y +-4．如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”（如822831=-，221653=-，则8，16均为“和谐数”），在不超过80的正整数中，所有的“和谐数”之和为（ ）A ．430B ．440C ．450D ．4605．下列各式中，不能用平方差公式计算的是（ ）A ．()()a b a b ---B ．()()22x y x y --+C ．()()222222x y x y -+D ．()()22a b c a b c +---6．若43a =，则()()()2111a a a -++的值为（ ）A ．4B ．2C ．0D ．2-7．计算822844(32)(32)(32)(32)+⨯+⨯+⨯+结果等于（ ）A ．1B ．316-216C ．332+232D ．332－2328．若规定m ⊕n =mn （m ﹣n ），则（a +b ）⊕（a ﹣b ）的值（ ）A ．2ab 2﹣2b 2B ．2a 2b ﹣2b 3C ．2a 2b +2b 2D ．2ab ﹣2ab 29．计算：(23)(23)x y x y ---+的结果，正确的是（ ）A ．2249x y -B ．2294y x -C ．2249x y +D ．2223x y -10．下列算式能用平方差公式计算的是（ ）A ．()()a b a b +--B ．22()(2)a b a b +-C ．(2)(2)x y x y +-D ．()()a b c a b c -++- 11．将图甲中明影部分的小长方形变换到图乙位置，根据两个图形的面积关系可以得到一个关于a 、b 的恒等式为（ ）A ．222()2a b a ab b -=-+B ．222()2a b a ab b +=++C ．22()()a b a b a b -+=-D ．2()a a b a ab -=-12．如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案，已知其中大正方形的面积为64，小正方形的面积为9．若用x ，y 分别表示小长方形的长与宽（其中x ＞y ），则下列关系式中错误的是（ ）A ．4964xy +=B ．8x y +=C ．3x y -=D ．229x y -= 13．计算（1212-）（1213-）……（1212020-）（1212021-）的值是（ ） A ．12 B ．12021 C ．20222021 D ．10112021二、填空题14．填空：（2a +b ）（______）=b 2﹣4a 215．已知|x ﹣1|+|y +2|＝0，则（2x +y ）（2x ﹣y ）＝___．16．一个长方体文具盒，长、宽、高如图所示（单位：cm ），该文具盒的体积是________3cm ．17．已知x a y b =⎧⎨=⎩是二元一次方程组2527x y x y +=⎧⎨+=⎩的解，则22a b -=________． 18．如图是一个数值转换器，若输入的数是2021，则输出的数是______．三、解答题19．用乘法公式简算（1）199×201 （2）20132﹣2014×201220．先化简，再求值．6x 2﹣（2x +1）（3x ﹣2）+（x +3）（x ﹣3），其中x ＝﹣2．21．若（x ﹣2）（x 2+ax ﹣8b ）的展开式中不含x 的二次项和一次项．（1）求b 的值；（2）求（a +1）（a 2+1）（a 4+1）…（a 32+1）+1的值．22．探究下面的问题：（1）如图⊕，在边长为a 的正方形中去掉一个边长为b 的小正方形（a b >），把余下的部分剪拼成如图⊕的一个长方形，通过计算两个图形（阴影部分）的面积，验证了一个等式，这个等式是______（用式子表示）；（2）运用你所得到的公式计算：⊕10.29.8⨯；⊕()()2323x y z x y z +---．参考答案1．A2．D 3．B 4．B 5．B 6．D 7．B 8．B 9．A 10．D11．C 12．D 13．D 14．b -2a15．016．（a 2-16）17．-818．202319．（1）39999；（2）1解：（1）原式=（200-1）×（200+1）=2002-12=40000-1=39999；（2）20132﹣（2013+1）×（2013-1）=20132-20132+1=1．20．x 2+x -7；-5解：原式=6x 2-6x 2+4x -3x +2+x 2-9=x 2+x -7，当x ＝﹣2时，原式= 2(2)(2)75-+--=-，21．（1）12b =-；（2）642 解：（1）2(2)(8)x x ax b -+-32282216x ax bx x ax b =+---+32(2)(28)16x a x a b x b =+--++展开式中不含x 的二次项和一次项，20280a a b -=⎧∴⎨+=⎩， 解得：212a b =⎧⎪⎨=-⎪⎩， 12b ∴=-； （2）当2a =时，2432(1)(1)(1)(1)1a a a a +++++2432(21)(21)(21)(21)(21)1=-+++++22432(21)(21)(21)(21)1=-++++4432(21)(21)(21)1=-+++64211=-+642=． 22．（1）a 2−b 2＝（a ＋b ）（a −b ）；（2）⊕99.96；⊕x 2−6xz ＋9z 2−4y 2 解：（1）图甲阴影面积＝a 2−b 2，图乙阴影面积＝（a ＋b ）（a −b ）， ⊕得到的等式为：a 2−b 2＝（a ＋b ）（a −b ），故答案为：a 2−b 2＝（a ＋b ）（a −b ）；（2）⊕10.2×9.8＝（10＋0.2）×（10−0.2）＝102−0.22＝100−0.04＝99.96；⊕()()2323x y z x y z +---＝（x −3z ＋2y ）（x −3z −2y ）＝（x −3z ）2−（2y ）2＝x 2−6xz ＋9z 2−4y 2．。

14.2.1 平方差公式-同步练习第1题. 2(1)_______1x x -=-答案：(1)x --第2题. 2200720062008-⨯的计算结果是（ ）Ａ．1Ｂ．－1 Ｃ．2 Ｄ．－2 答案：Ａ第3题. 简便计算：10397⨯．答案：9991第4题. 2(2)(2)(4)b b b +-+答案：416b - 第5题. 试说明：两个连续奇数的积加上1，一定是一个偶数的平方．答案：设两个连续奇数为21n -，21n +，则22(21)(21)1(2)11(2)n n n n -++=-+=，结果成立．第6题. 方程22(21)(13)5(1)(1)x x x x ---=-+的解是（ ）Ａ．2x =-Ｂ． 2.5x =- Ｃ．2x = Ｄ． 2.5x = 答案：Ｄ第7题. 下列各式中，能用平方差公式计算的是（ ） Ａ．1122a b a b ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭Ｂ．1122a b a b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭ Ｃ．1122a b a b ⎛⎫⎛⎫--- ⎪⎪⎝⎭⎝⎭ Ｄ．1122a b a b ⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭ 答案：Ｃ 第8题. 计算:（1）()(2)a b a +-； （2）1122x x ⎛⎫⎛⎫-+ ⎪⎪⎝⎭⎝⎭； （3）()()m n m n +-； （4）(0.1)(0.1)x x -+；（5）()()x y y x +-+．答案：（1）222a ba a b +--；（2）214x -；（3）22m n -；（4）20.01x -；（5）22x y -．第9题. 计算：（1）(25)(25)a a ---； （2）11113232a b a b ⎛⎫⎛⎫-+-- ⎪⎪⎝⎭⎝⎭； （3）(53)(35)ab x x ab ---； （4）11122(8)224x x x x ⎛⎫⎛⎫-+-+ ⎪⎪⎝⎭⎝⎭； （5）111()933x y x y x y x y ⎛⎫⎛⎫⎛⎫----+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． 答案：（1）2254a -；（2）221194a b -；（3）222925x a b -；（4）24x --；（5）21029y xy -．第10题. 利用平方差公式计算：（1）3129⨯；（2）9.910.1⨯；（3）98102⨯；（4）1003997⨯．答案：（1）(301)(301)9001899+-=-=；（2）(100.1)(100.1)1000.0199.99-+=-=；（3）(1002)(1002)1000049996-+=-=；（4）(10003)(10003)10000009999991+-=-=．第11题. 计算：（1）(34)(34)a b a b +-； （2）()()a b c a b c +-++；（3）112233a c b a c b ⎛⎫⎛⎫-++--+ ⎪⎪⎝⎭⎝⎭．答案：（1）22916a b -； （2）22()a b c +-(或2222a ab b c ++-)；（3）22123a b c ⎛⎫-+- ⎪⎝⎭22214493a ab b c ⎛⎫-+- ⎪⎝⎭或．第12题. 利用平方差公式计算：（1）2733⨯；（2）5.9 6.1⨯；（3）99101⨯；（4）1005995⨯．答案：（1）891；（2）35.99；（3）9999；（4）999975．第13题. 如图是四张全等的矩形纸片拼成的图形，请利用图中空白部分面积的不同表示方法，写出一个关于a 、b 的恒等式 ．答案：如：22()4()a b ab a b +-=-．第14题. 2302＝_________答案：91204第15题. 22(4)a b -=_________答案：224168a ab b -+第16题. 若2154a b ab +==，，则22a b +=_________ 答案：1142第17题. 如果226x x k ++恰好是一个整式的平方，那么常数k 的值为（ ） Ａ．3 Ｂ．3- Ｃ．3± Ｄ．9ab答案：Ｃ第18题. 22()x y --等于（ ）Ａ．222x xy y --+Ｂ．4222x x y y --+ Ｃ．4222x x y y ++Ｄ．422x xy y --答案：Ｃ第19题. 计算题：（1）2(23)a b c --；（2）2(2)(2)()x y z x y z x y z +----+-．答案：（1）222494612a b c ab ac bc ++--+；（2）2522y xy yz --+．第20题. 已知2222263()()x y xy x y x y +==+-和，，求的值．答案：2()32x y +=，2()20x y -=第21题. 已知2(1)()5a a a b ---=，求222a b ab +-的值． 答案：252第22题. 2212x ⎛⎫+ ⎪⎝⎭等于（ ） Ａ．42124x x ++ Ｂ．4214x x -+ Ｃ．4214x x ++ Ｄ．42124x x -+ 答案：Ｃ第23题. 若14a a -=，则221a a +＝_________． 答案：18第24题. 代数式26()a b -+的最大值是_______，这时a 与b 的关系为________． 答案：6，0a b +=或a b ，互为相反数第25题. 计算：2222x y x y +-⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭． 答案：222x y +．第26题. 已知5,6,a b ab +==-求下列各式的值．（1）22a b +； （2）22a ab b -+． 答案：（1）222()2251237a b a b ab +=+-=+=；（2）()()22223536251843a ab b a b ab -+=+-=-⨯-=+=．第27题. 在多项式241x +中，添加一个单项式，使其成为一个完全平方式．则添加的单项式是 （只写出一个即可）答案：4x ±或1-或24x -第28题. 已知：如图，现有a a ⨯、b b ⨯的正方形纸片和a b ⨯的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为22252a ab b ++，并标出此矩形的长和宽．a aab bb答案：说明：答案不唯一，画图正确，不论画在什么位置，只要符合题意即可．不标出相应尺寸的扣2分，标错1个或少标1个扣1分．第29题. 62()()ab ab ÷= （ ）Ａ．33a b Ｂ．44a b Ｃ．34a b Ｄ．43a b答案：Ｂ a+2b 2a +b 拼法一拼法二 2a +b a+2b。

人教版八年级数学上册《14.2.1平方差公式》同步练习题带答案学校:___________班级：___________姓名：___________考号：___________一、单选题1．计算：226535-=（ ） A ．30B ．300C ．900D ．30002．()()3232y y +-=（ ） A ．294y +B ．294y -C ．292y +D ．292y -3．若234a a -=，则代数式(1)(1)3(2)a a a +--+的值为（ ） A ．5-B ．3-C ．3D ．54．若()()22291111810n--=⨯，则n 的值是（ ）A ．12B ．10C ．8D ．89⨯5．若224=a b -，则()()22a b a b +-的值是（ ） A ．24B ．16C ．8D ．46．()()a b c a b c -++-等于（ ） A ．()2a b c --+ B ．()22a b c -- C ．()22a b c -- D ．222c a b -+7．若12a b -=，则22--a b b 的值为（ ） A ．12B ．14C ．1D ．28．若一个正整数能表示成另两个正整数的平方差，即22x a b =-（其中a 、b 、x 为正整数），则称这个正整数为完美数．下列各数中不是完美数的是（ ） A ．2022B ．2021C ．2020D ．20199．从边长为a 的大正方形纸板正中央挖去一个边长为b 的小正方形后，将其裁成四个大小和形状完全相同的四边形（如图1），然后拼成一个平行四边形（如图2），那么通过计算两个图形阴影部分的面积，可以验证成立的等式为（ ）A ．()222a b a b -=- B ．()2222a b a ab b +=++C ．()2222a b a ab b -=-+D ．()()22a b a b a b -=+-10．如图，边长为a 的大正方形剪去一个边长为b 的小正方形后，将剩余部分通过割补拼成新的图形，根据图形能验证的等式为（ ）A ．()222a b a b -=- B ．()2222a b a ab b +=++C ．()2222a b a ab b -=-+D ．()()22a b a b a b -=+-二、填空题11．若()2222221)22115a b a b +++-=（，则22a b += ． 12．若02023a =，2202220212023b =-⨯则a ，b 的数量关系为 ． 13．计算：111331933x x x x的结果是 ． 14．若29m =，23n =则()()m n m n +-= ．15．若正方形的边长增加3cm ，其面积增加227cm ，则该正方形的边长是 cm ．三、解答题16．化简：()()()2262x y x y xy xy x +-+-÷．17．先化简，再求值：()()()32232393x x x x x -+---÷⎡⎤⎣⎦，其中3x =．18．化简求值：()()222224xy xy x y xy ⎡⎤+--+÷⎣⎦，其中5x = 110y =-．19．阅读下面问题：你能化简()()999811a a a a -++⋅⋅⋅++吗？我们不妨先从简单情况入手，发现规律，归纳结论．(1)先填空：()()11a a -+=______；()()211a a a -++=_______； ()()3211a a a a -+++=______；…由此猜想()()999811a a a a -++⋅⋅⋅++=________．(2)利用得出的结论计算：()1991981972222221+++⋅⋅⋅+++20．如图①，从边长为a 的大正方形中剪掉一个边长为b 的小正方形，将阴影部分沿线剪开，如图所示，拼成图①的长方形．(1)【探究】①请你分别表示出这两个图形中阴影部分的面积__________；__________；①比较两图的阴影部分面积，可以得到乘法公式：____________________（用字母表示）； (2)【应用】请应用这个公式完成计算：20011999⨯．参考答案1．D【分析】根据平方差公式进行计算即可． 【详解】解：226535-()()65356535=+- 10030=⨯3000=故选：D ．【点睛】本题主要考查了利用平方差公式进行计算，熟练掌握平方差公式()()22a b a b a b +-=- 是解题的关键．2．B【分析】根据平方差公式计算即可．平方差公式：两个数的和与这两个数的差相乘，等于这两个数的平方差．【详解】解：（3+2y ）（3-2y ） =32-（2y ）2 =9-4y 2． 故选：B ．【点睛】本题考查了平方差公式，熟记公式是解答本题的关键． 3．B【分析】先进行整式的混合运算将原式化简，再整体代值计算即可． 【详解】解：()()()1132a a a +--+ 2136a a =--- 237a a =--47=- 3=-．故选：B ．【点睛】本题考查了整式的化简求值，熟练掌握运算法则是解本题的关键． 4．A【分析】利用平方差公式将原式变形为()()()()9191111111n+-+-，可得1081210n⨯⨯⨯，从而得到n 值．【详解】解：()()2291111n--=()()()()9191111111n+-+-=1081210n⨯⨯⨯=281012n⨯⨯=2810⨯ ①n =12故选A ．【点睛】本题考查了平方差公式的应用，解题的关键是利用平方差公式将已知式子变形． 5．B【分析】把()()22a b a b +-利用平方差公式先运算底数，再代入数据计算即可． 【详解】()()()()()222222==a b a b a b a b a b +-+-⎤-⎡⎣⎦又224=a b -∴()()()222222==4=16a b a b a b +--．故答案为：B ．【点睛】本题考查了平方差公式的应用，先利用平方差公式计算底数可以使运算更简便． 6．B【分析】把原式()()a b c a b c -++-变形为()()a b c a b c --+-⎡⎤⎡⎤⎣⎦⎣⎦利用平方差公式进行计算即可．【详解】解：()()a b c a b c -++-()()a b c a b c =--+-⎡⎤⎡⎤⎣⎦⎣⎦()22a b c =--故选：B【点睛】此题考查了平方差公式，熟练掌握平方差公式的内容是解题的关键． 7．B【分析】先利用平方差公式，得22--a b b =()()a b a b b -+-，再整体代入化简求值即可． 【详解】解：①12a b -=①22--a b b =()()a b a b b -+-=()12a b b +-=()111222a b a b -=-=1122⨯=14． 故选B ．【点睛】本题主要考查代数式求值，掌握整式的混合运算法则以及平方差公式是解题的关键． 8．A【分析】设k 是正整数，证明除1外，所有的奇数都是完美数；除4外，所有的能被4整除的偶数都是完美数，即可得答案．【详解】解：设k 是正整数①()()()2211121k k k k k k k +-=+++-=+ ①除1外，所有的奇数都是完美数 ①B ，D 选项都是完美数，不符合题意； ①()()()()221111114k k k k k k k +--=++-+-+= ①除4外，所有的能被4整除的偶数都是完美数 所以C 选项是完美数，不符合题意A 选项2022不是奇数也不是4的倍数，不是完美数，符合题意． 故选：A ．【点睛】本题考查了平方差公式分解因式的应用，牢记()()22a b a b a b -=+-）是解题的关键． 9．D【分析】本题主要考查了平方差公式，运用不同方法表示阴影部分面积是解题的关键． 【详解】解：图1中阴影部分的面积为：22a b -，图2中阴影部分的面积为：()()a b a b +- ①两图中阴影部分的面积相等()()22a b a b a b ∴-=+-①可以验证成立的公式为()()22a b a b a b -=+-故选：D ． 10．D【分析】本题考查了利用几何方法验证平方差公式，解决问题的关键是根据拼接前后不同的几何图形的面积不变得到等量关系．边长为a 的大正方形剪去一个边长为b 的小正方形后的面积为22a b -，新的图形面积等于()()a b a b -+，由于两图中阴影部分面积相等，即可得到结论．【详解】图中剩余部分的面积等于两个正方形的面积之差，即22a b - 剩余部分通过割补拼成的平行四边形的面积为()()a b a b -+ ①前后两个图形中阴影部分的面积相等①()()22a b a b a b -=+-故选：D ． 11．2【分析】设22a b x +=，将()()222222122115a b a b +++-=变为：()()212115x x +-=，解出x 的值，根据20a ≥，20b ≥得出220a b +≥，即0x ≥，即可得出答案．【详解】解：设22a b x +=，则()()222222122115a b a b +++-=可变为：()()212115x x +-=①24115x -= 即24x = ①2x =± ①20a ≥ 20b ≥ ①220a b +≥，即0x ≥ ①2x =-舍去 ①222a b x +==． 故答案为：2．【点睛】本题主要考查了代数式求值，解题的关键是注意整体思想． 12．a b =【分析】由平方差公式计算出b 的值，由零指数幂计算出a 的值，比较即可得数量关系． 【详解】解：2202220212023b =-⨯ 22022(20221)(20221)=--⨯+ 222022(20221)=--1=而012023a == ①a b =故答案为：a b =．【点睛】本题考查了平方差公式的运用，零指数幂等知识，灵活运用平方差公式是解题的关键． 13．0【分析】本题考查了整式的运算，利用平方差公式计算即可【详解】解：()()111331933x x x x ⎛⎫⎛⎫+-+-+ ⎪⎪⎝⎭⎝⎭2219199x x ⎛⎫=-+- ⎪⎝⎭229119x x =-+-0=．故答案为：0． 14．6【分析】本题考查平方差公式，利用平方差公式进行求解即可． 【详解】解：①29m = 23n =①()()226m n m n m n +-=-=；故答案为：6． 15．3【分析】本题考查用方程解应用题，涉及平方差公式、解一元一次方程，设该正方形的边长是cm x ，根据等量关系列方程求解即可得到答案，读懂题意，列方程求解是解决问题的关键． 【详解】解：设该正方形的边长是cm x ，则()22327x x +-=，解得3x =∴设该正方形的边长是3cm故答案为：3． 16．23x y -【分析】根据平方差公式，多项式除以单项式，进行计算即可求解． 【详解】解：原式2222262x y xy x xy x =-+÷-÷2223x y y y =-+- 23x y =-【点睛】本题考查了平方差公式，多项式除以单项式，掌握平方差公式，多项式除以单项式的运算法则是解题的关键． 17．21x -+ 5-【分析】先去小括号，然后合并同类项，再计算多项式除以单项式，最后把x 的值代入化简后的式子进行计算即可解答．【详解】解：[（3﹣2x ）（2x +3）﹣x （2x ﹣3）﹣9]÷3x ＝（9﹣4x 2﹣2x 2+3x ﹣9）÷3x ＝（﹣6x 2+3x ）÷3x ＝﹣2x +1当x ＝3时，原式＝﹣2×3+1 ＝﹣6+1 ＝﹣5．【点睛】本题考查了整式的混合运算﹣化简求值，准确熟练地进行计算是解题的关键． 18．xy -12【分析】先利用平方差公式去小括号，再合并同类项，最后计算除法，然后把x 、y 的值代入计算即可．【详解】解：原式()2222424x y x y xy =--+÷22x y xy =-÷xy =-当5x =，110y =-时 原式＝﹣5×（110-） 12=． 【点睛】本题考查了整式的化简求值，解题的关键是熟练掌握运算法则． 19．(1)21a - 31a - 41a - 1001a - (2)20021-【分析】本题主要考查平方差公式的应用，多项式乘法中规律性问题，掌握题中规律并正确计算是解题的关键．（1）根据平方差公式可得①，根据多项式乘多项式可求①、①，根据①、①、①规律可求①； （2）将式子乘以()21-，利用（1）中规律求解即可．【详解】（1）解：①()()2111a a a -+=- ①()()232231111a a a a a a a a a -++=++---=-①()()324323241111a a a a a a a a a a a a -+++=+++----=- ①由此猜想()()9998100111a a a a a -++⋅⋅⋅++=-故答案为：21a - 31a - 41a - 1001a -； （2）解：1991981972222221+++⋅⋅⋅+++ ()()199198197221222221=-+++⋅⋅⋅+++20021=-．20．(1)①22a b - ()()a b a b +- ①22()()a b a b a b +-=-； (2)3999999．【分析】（1）①、图①阴影部分的面积为两个正方形面积的差，图①阴影部分的面积是长为()a b +，宽为()a b -的长方形面积；①、图①阴影部分的面积和图①阴影部分的面积相等，即可列出式子；（2）将20011999⨯转化为(20001)(20001)+-，根据平方差公式进行计算即可． 【详解】（1）解：①、在图①中：大正方形的面积为2a ，小正方形的面积为2b ∴阴影部分的面积为：22a b -；在图①中：阴影部分为长方形，且长为()a b +，宽为()a b - ∴阴影部分的面积为：()()a b a b +-；①、图①阴影部分的面积和图①阴影部分的面积相等 ∴可得到乘法公式：22()()a b a b a b +-=-；（2）原式2(20001)(20001)200013999999=+-=-=．【点睛】本题考查平方差公式的几何意义和平方差公式的应用，用代数式表示阴影部分的面积是得出平方差公式的关键．。

14.2 乘法公式14.2.1 平方差公式课前预习要点感知 (a ＋b)(a －b)＝________．即两个数的和与这两个数的差的积，等于这两个数的________．这个公式叫做________公式．预习练习1－1 在下列多项式的乘法中，可以用平方差公式进行计算的是( ) A ．(x ＋1)(1＋x) B ．(12a ＋b)(b －12a)C ．(－a ＋b)(a －b)D ．(x 2－y)(x ＋y 2) 1－2 计算：(1)(x ＋3)(x －3); (2)(a ＋2b)(a －2b)．当堂训练知识点1 用面积法证明平方差公式1．将图1中阴影部分的小长方形变换到图2位置，你根据两个图形的面积关系得到的数学公式是________________________．图1 图22．如图1，从边长为a 的正方形纸片中剪去一个边长为b 的小正方形，再沿着线段AB 剪开，把剪成的两张纸片拼成如图2的等腰梯形．图1 图2(1)设图1中阴影部分面积为S 1，图2中阴影部分面积为S 2，请直接用含a ，b 的代数式表示S 1，S 2；(2)请写出上述过程所揭示的乘法公式．知识点2 直接利用平方差公式计算 3．计算：(1)(14a －1)(14a ＋1)；(2)(2m ＋3n)(2m －3n)．4．先化简，再求值：(1＋3x)(1－3x)＋x(9x ＋2)－1，其中x ＝12.知识点3 利用平方差公式解决问题 5．计算：(1)1 007×993；(2)2 014×2 016－2 0152.课后作业6．下列各式中，能用平方差公式计算的是( ) ①(7ab －3b)(7ab ＋3b)；②73×94； ③(－8＋a)(a －8)；④(－15－x)(x －15)． A ．①③ B ．②④ C ．③④ D ．①④7．对于任意正整数n ，能整除式子(m ＋3)(m －3)－(m ＋2)(m －2)的整数是( ) A ．2 B ．3 C ．4 D ．58．计算(x 2＋14)(x ＋12)(x －12)的结果为( )A ．x 4＋116B ．x 4－116C ．x 4－12x 2＋116D ．x 4－18x 2＋1169．两个正方形的边长之和为5，边长之差为2，那么用较大的正方形的面积减去较小的正方形的面积，差是________．10．已知(a ＋b －3)2＋(a －b ＋5)2＝0，则a 2－b 2＝________． 11．计算：(1)(－12x 2＋2)(－12x 2－2)；(2)(－x －y)(x －y)；(3)(a ＋2b)(a －2b)－12b(a －8b)；(4)2132－214×212.12．(贵阳中考)先化简，再求值：(x ＋1)(x －1)＋x 2(1－x)＋x 3，其中x ＝2.13．解方程：(3x)2－(2x＋1)(3x－2)＝3(x＋2)(x－2)．挑战自我14．已知x≠1，计算：(1＋x)(1－x)＝1－x2，(1－x)(1＋x＋x2)＝1－x3，(1－x)(1＋x＋x2＋x3)＝1－x4.(1)观察以上各式并猜想：(1－x)(1＋x＋x2＋…＋x n)＝________；(n为正整数)(2)根据你的猜想计算：①(1－2)(1＋2＋22＋23＋24＋25)＝________；②2＋22＋23＋…＋2n＝________(n为正整数)；③(x－1)(x99＋x98＋x97＋…＋x2＋x＋1)＝________；(3)通过以上规律请你进行下面的探索：①(a－b)(a＋b)＝________；②(a－b)(a2＋ab＋b2)＝________；③(a－b)(a3＋a2b＋ab2＋b3)＝________．参考答案要点感知 a 2－b 2平方差 平方差预习练习1－1 B 1－2 (1)原式＝x 2－9. (2)原式＝a 2－(2b)2＝a 2－4b 2. 当堂训练1．(a ＋b)·(a －b)＝a 2－b 2 2.(1)S 1＝a 2－b 2，S 2＝12(2b ＋2a)(a －b)＝(a ＋b)(a －b)． (2)(a ＋b)(a －b)＝a 2－b 2. 3.(1)原式＝116a 2－1. (2)原式＝(2m)2－(3n)2＝4m 2－9n 2. 4.原式＝1－9x 2＋9x 2＋2x －1＝2x.当x ＝12时，原式＝2×12＝1.5．(1)原式＝(1 000＋7)×(1 000－7)＝1 0002－72＝999 951. (2)原式＝(2 015－1)×(2 015＋1)－2 0152＝2 0152－1－2 0152＝－1. 课后作业6．D 7.D 8.B 9.10 10.－15 11.(1)原式＝(－12x 2)2－22＝14x 4－4. (2)原式＝(－y)2－x 2＝y 2－x 2. (3)原式＝a 2－(2b)2－12ab ＋4b 2＝a 2－12ab. (4)原式＝2132－(213＋1)×(213－1)＝2132－(2132－1)＝1. 12.原式＝x 2－1＋x 2－x 3＋x 3＝2x 2－1.当x ＝2时，原式＝2×22－1＝7. 13.9x 2－(6x 2－4x ＋3x －2)＝3(x 2－4)，9x 2－6x 2＋4x －3x ＋2＝3x 2－12，x ＝－14. 挑战自我 14．(1)1－xn ＋1(2)①－63 ②2n ＋1－2 ③x 100－1 (3)①a 2－b 2②a 3－b 3③a 4－b 4提示：(2)②原式＝2(1＋2＋22＋…＋2n －1)＝－2(1－2)(1＋2＋22＋…＋2n －1)＝－2(1－2n )＝－2＋2·2n ＝2n ＋1－2.③原式＝－(1－x)(1＋x ＋x 2＋…＋x 97＋x 98＋x 99)＝－(1－x 100)＝x 100－1.。

新人教版数学八年级上册第十四章第二节平方差公式课时练习一、选择题（每小题5分，共30分）1.下列多项式的乘法中，能用平方差公式计算的是（）A.(1+x)(x+1)B.(0.5a+b)(b-0.5a)C.(-m+n)(m-n)D.(m+2n)(-2n-m)答案：B知识点：平方差公式解析：解答：A.(1+x)(x+1)，x，1的符号相同，∴不能用平方差公式计算，故此选项错误；B.(0.5a+b)(b—0.5a) ，b符号相同，0.5a符号相反，∴能用平方差公式计算，故此选项正确；C.(-m+n)(m-n) ，m，n的符号相反，∴不能用平方差公式计算，故此选项错误；D.(m+2n)(-2n—m) ，m，2n的符号相反，∴不能用平方差公式计算，故此选项错误；分析：根据平方差公式的特点要找相同项和相反项，其结果是相同项的平方减去相反项的平方，只有B符合特点才能计算.故选B.2.计算（3a-bc）(-bc-3a)的结果为（）A.b2c2+9a2B.b2c2-3a2C.-b2c2-9a2D.-9a2+b2c2答案：D.知识点：平方差公式解析：解答：（3a-bc）(-bc-3a)=（3a-bc）[-(3a+bc)]=-(9a2-b2c2)=-9a2+b2c2分析：根据平方差公式的特点要找相同项和相反项，其结果是相同项的平方减去相反项的平方.故选D.3.下列运算正确的等式是（）A.(5-m)(5+m)=m2-25B.(1-3m)(1+3m)=1-3m2C.(-4-3n)(-4+3n)= -9n2+16D.(2ab-n)(2ab+n)=4ab2-n2知识点：平方差公式解析：解答：A.(5-m)(5+m)= 25-m2，所以此选项是错误的；B.(1-3m)(1+3m)=1-9m2，所以此选项是错误的；C.(-4-3n)(-4+3n)= -9n2+16，此选项是正确；D.(2ab-n)(2ab+n)=4a2b2-n2，所以此选项是错误的；分析：根据平方差公式的特点要找相同项和相反项，其结果是相同项的平方减去相反项的平方.故选C.4.与x2-4y2相等的式子是（）A.(-2y+x)(-2y-x)B.(-2y+x)(2y-x)C.(x+y)(x-4y)D.(-2y-x)(2y-x)答案：D.知识点：平方差公式解析：解答：x2-4y2=（x-2y）(x+2y)=(-2y-x)(2y-x)分析：根据利用平方差公式的逆运算，把式拆分成（a+b）(a-b)即可找到相同结果.故选D.5.(a+2)(a2+4)(a-2) 的计算结果为（）A.a4+16B.a4-16C.-a4-16D.16-a4答案：B.知识点：平方差公式解析：解答：(a+2)(a2+4)(a-2)=(a2+4) (a2-4)= a4-16分析：根据利用平方差公式即可求出结果.故选B.6.设x+y+z=6，x+y-z=7，则（x+y）2-z2的值是（）A.13B.42C.1D.30知识点：平方差公式解析：解答：（x+y）2-z2=（x+y+z）（x+y-z）=42分析：把x+y看成a项，z看成b项，利用平方差公式即可求出结果.故选B.7.下列可以用平方差公式计算的是（）A.(2a-3b)(-2a+3b)B.(- 4b-3a)(-3a+4b)C.(a-b)(b-a)D.(2x-y) (2y+x) 答案：B.知识点：平方差公式解析：解答：A.(2a-3b)(-2a+3b)，2a,3b的符号相反，∴不能用平方差公式计算，故此选项错误；B.(- 4b-3a)(-3a+4b)，3a,符号相同，4b符号相反，∴能用平方差公式计算，故此选项正确；C.(a-b)(b-a)，a，b的符号相反，∴不能用平方差公式计算，故此选项错误；D.(2x-y) (2y+x)，2x和x不是相同项，2y和y不是相同项，∴不能用平方差公式计算，故此选项错误.分析：根据利用平方差公式计算.故选B.8.若x≠y,则下列各式不能成立的是（）A.(x-y)2=(y-x)2B.(x-y)3=-(y-x)3C.(x+y)(y-x)=(x+y)(x-y)D.(x+y)2=(-x-y)2答案：C.知识点：平方差公式.解析：解答：A.(x-y)2=(y-x)2计算正确；B.(x-y)3=-(y-x)3计算正确；C.(x+y)(y-x) ≠(x+y)(x-y)，故本题错误；D.(x+y)2=(-x-y)2计算正确；分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选C.9.下列式子中，计算结果是4x2-9y2的是（）A. (2x-3y)2B. (2x+3y)(2x-3y)C. (-2x+3y)2D. (3y+2x)(3y-2x)知识点：平方差公式解析：解答： 4x 2-9y 2=(2x-3y)(2x+3y)分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选B.10.已知a+b=4,a-b=3,则a 2-b 2=( )A.4B.3C.12D.1答案：C.知识点：平方差公式解析：解答：a 2-b 2=(a+b)(a-b)=4×3=12.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选C.11.下列算式能用平方差公式计算的是（ ）A.（2a+b ）(2b-a)B.(21 x+1)(- 21-1) C.(3x-y)(-3x+y) D.(-x-y)(-x+y) 答案：D.知识点：平方差公式解析：解答：A.（2a+b ）(2b-a)不符合（a+b ）(a-b)公式，所以不能用平方差公式. B.(21 x+1)(- 21-1) 不符合（a+b ）(a-b)公式，所以不能用平方差公式. C.(3x-y)(-3x+y) 不符合（a+b ）(a-b)公式，所以不能用平方差公式.D.(-x-y)(-x+y)=（-x ）2-y 2=x 2-y 2.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选D.12.计算（a+b ）(-a+b)的结果是（ ）A.b 2-a 2B.a 2-b 2C.-a 2-2ab+b 2D.-a 2+2ab+b 2答案：A.知识点：平方差公式解析：解答：（a+b ）(-a+b)=（b+a ）(b-a)= b 2-a 2.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.13.计算（x-3）(x+3)的结果是（ ）A.x 2-9B.x 2-3C.x 2-6D.9-x 2答案：A.知识点：平方差公式解析：解答：（x-3）(x+3)=x 2-9.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选A.14.计算2009×2011-20102的结果是（ ）A.1B.-1C.2008D.-2008答案：B.知识点：平方差公式解析：解答：原式=（2010+1）(2010-1)- 20102=20102-1-20102=-1.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选B.15.若三角形的底边长为2a+1,高为2a-1,则此三角形的面积为（）A.4a 2-1B.4a 2-4a+1C.4a 2+4a+1D.2a 2-21答案：D.知识点：平方差公式解析： 解答：三角形面积为：21（2a+1）（2a-1）=2a 2-21.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.故选D.二、填空题（每小题5分，共25分）16.（-1-3x ）(____________)=1-9x 2答案：-1+3x.知识点：平方差公式解析：解答：（-1-3x ）(____________)=1-9x 2（-1-3x ）(-1+3x)=1-9x 2.分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.17.(a+1)(a-1)(a2+1)=_________________________答案：a4-1.知识点：平方差公式解析：解答：(a+1)(a-1)(a2+1)=(a2-1) (a2+1)= a4-1分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.18. (a+b)(-b+a)=________答案：a2-b2.知识点：平方差公式解析：解答：(a+b)( -b+a)= a2- b2分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.19. (x+1)(x-1)-(x-2)(x+2)=___________答案： 3.知识点：平方差公式解析：解答：原示=(x2-1)-(x2-4)=3分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.20.已知a+b=3,a-b=5,则代数式a2-b2的值是答案： 15.知识点：平方差公式解析：解答：a2-b2=(a+b)(a-b)=3×5=15分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.三、解答题（每题10分，共50分）21. 计算9x2-4y2，当x=1，y=1时的结果答案： 5.知识点：平方差公式解析：解答：9x 2-4y 2=(3x+2y)(3x-2y)，代入x=1，y=1，原式=5×1=5分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.22. 计算（31a+b ）（31a-b ） 答案：91a 2-b 2. 知识点：平方差公式解析： 解答：（31a+b ）（31a-b ）=91a 2-b 2 分析：本题考查了平方差公式，掌握运算法则是解答本题的关键.23.计算：(a+b-1)（a-b+1）答案：a 2-b 2-1+2b.知识点：平方差公式解析：解答：(a+b-1)（a-b+1）= a 2-(b-1)2=a 2-b 2-1+2b分析：本题首先的是学生能找出（a+b ）(a-b)公式，同时考查了平方差公式，掌握运算法则是解答本题的关键. 24.求3031 ×2932的值. 答案：89998. 知识点：平方差公式解析：解答：原式=(30+31)（30-31）= 900-91=89998 分析：本题首先的是学生能找出（a+b ）(a-b)公式，同时考查了平方差公式，掌握运算法则是解答本题的关键.25.已知一个长方体的长为2a ，宽也是2a ，高为h.(1)用a 、h 的代数式表示该长方体的体积与表面积.(2)当a=3，h=21时，求相应长方体的体积与表面积. (3)在(2)的基础上，把长增加x ，宽减少x ，其中0＜x ＜6，问长方体的体积是否发生变化，并说明理由.答案：(1) 体积=a 2h ；表面积=8a 2+8ah ；(2)体积是18，表面积是84；(3)18-21x 2＜18，体积缩小了.知识点：平方差公式 列代数式 求代数式的值解析： 解答： (1)长方体体积=2a ×2a ×h=4a 2h ，长方体表面积=2×2a ×2a+4×2ah=8a 2+8ah ；(2)当a=3，h=21时，长方体体积=4×32×21=18；长方体表面积=8×32+8×3×21=84. (3)当长增加x ，宽减少x 时，长方体体积=21×(6+x)(6-x)= 18-21x 2＜18，故长方体体积减小了. 分析：(1)、(3)根据长方体的体积与表面积公式进行计算即可；(2)把a=3，h=21代入(1)的关系式进行计算.。