下载文档原格式
平面一般力系的二力矩式平衡方程平面一般力系的二力矩式平衡方程引言在物理学和工程学中，力学的平衡是一个重要的概念。
力学的平衡可以分为平面力系的平衡和空间力系的平衡。
在本文中，我们将讨论平面力系的平衡，并重点关注二力矩式平衡方程。
平面力系的定义和特点平面力系是指作用在一个平面内的一组力。
平面力系具有以下特点：1. 所有的力和力矩都在一个平面内；2. 力系中的力可以同时作用在一个物体的不同点上；3. 力系中的力可能会产生力矩。
力矩的概念力矩是指力对旋转物体造成的影响。
它由两个因素确定：力的大小和作用点与旋转轴的距离。
力矩的大小可以通过以下公式计算：M = Fd其中，M表示力矩，F表示力的大小，d表示力的作用点与旋转轴之间的距离。
力矩的方向可以通过以下规则确定：1. 如果力的作用点在旋转轴上，力矩的大小为零；2. 如果力由旋转轴向外作用，力矩的方向为顺时针方向；3. 如果力由旋转轴向内作用，力矩的方向为逆时针方向。
二力矩式平衡方程的推导在平面力系中，如果力系处于平衡状态，那么力系的合力和合力矩都必须为零。
根据牛顿第一定律，合力为零意味着物体的加速度为零；根据牛顿第二定律，合力矩为零意味着物体的角加速度为零。
设平面力系中共有n个力，分别记为F1, F2, ..., Fn。
考虑到每个力都可以产生力矩，那么每个力产生的力矩之和为：M1 + M2 + ... + Mn = 0力矩的正负号要根据力矩的方向来确定，根据上述力矩的规则，如果力矩是顺时针方向的，那么取正号；如果力矩是逆时针方向的，那么取负号。
根据力矩的计算公式，将每个力的力矩带入上述方程，得到二力矩式平衡方程：F1d1 + F2d2 + ... + Fndn = 0这就是平面力系的二力矩式平衡方程。
应用实例下面通过一个实例来说明如何应用二力矩式平衡方程。
假设有一个悬臂梁，上面有一个重物挂着。
悬臂梁的长度为L，重物的质量为m，重物与悬臂梁的连接处距离悬臂梁固定点的距离为d。
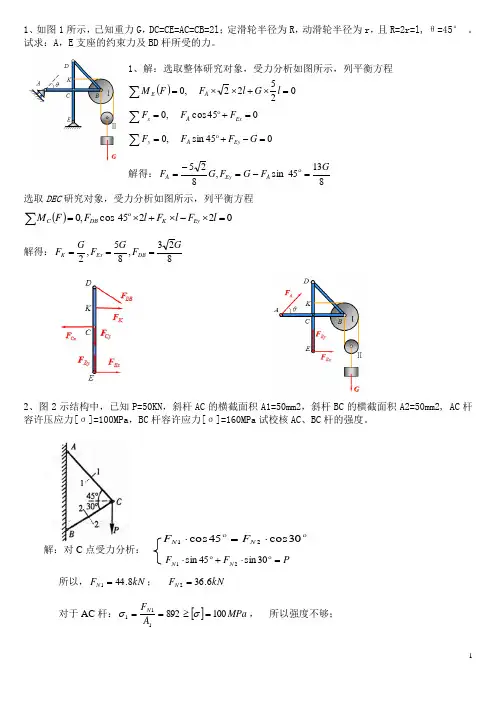
1、如图1所示，已知重力G ，DC=CE=AC=CB=2l ；定滑轮半径为R ，动滑轮半径为r ，且R=2r=l, θ=45° 。
试求：A ，E 支座的约束力及BD 杆所受的力。
1、解：选取整体研究对象，受力分析如图所示，列平衡方程()045sin ,0045 cos ,002522,0=-+==+==⨯+⨯⨯=∑∑∑G F F FF F F lG l F F M Ey A yEx A xA E解得：81345 sin ,825GF G F G F A Ey A =-=-=选取DEC 研究对象，受力分析如图所示，列平衡方程()02245 cos ,0=⨯-⨯+⨯=∑l F l F l FF M Ey K DBC解得：823,85,2GF G F G F DB Ex K ===2、图2示结构中，已知P=50KN ，斜杆AC 的横截面积A1=50mm2，斜杆BC 的横截面积A2=50mm2, AC 杆容许压应力[σ]=100MPa ，BC 杆容许应力[σ]=160MPa 试校核AC 、BC 杆的强度。
解：对C 点受力分析：所以，kN F N 8.441=； kN F N 6.362= 对于AC 杆：[]MPa A F N 100892111=≥==σσ， 所以强度不够； 30cos 45cos 21⋅=⋅N N F F P F F N N =⋅+⋅30sin 45sin 21对于BC 杆：[]MPa A F N 160732222=≥==σσ， 所以强度不够。
3、图3传动轴上有三个齿轮，齿轮2为主动轮，齿轮1和齿轮3消耗的功率分别为KW 756.0和KW 98.2。
若轴的转速为min /5.183r ，材料为45钢，[]MPa 40=τ。
根据强度确定轴的直径。
3、解:(1) 计算力偶距 m N nP m .3.39954911== m N nP m .155954933== m N m m m .3.194312=+=(2) 根据强度条件计算直径从扭矩图上可以看出，齿轮2与3 间的扭矩绝对值最大。
九平面一般力系平衡方程的其他形式平面一般力系的平衡方程是描述物体在平面上受力平衡的基本方程，也称为平面力的三元方程。
这个方程可以通过向量和标量形式来表示。
除了常见的三元方程表示外，还可以通过力矩和分力来表示。
首先，我们来回顾一下平面一般力系平衡方程的基本形式。
设物体在平面上受到多个力的作用，这些力可以分解为水平方向的分力和竖直方向的分力。
根据受力平衡的条件，水平方向的分力之和为零，竖直方向的分力之和也为零。
设水平方向的分力之和为Rx，竖直方向的分力之和为Ry，那么平面一般力系的平衡方程可以表示为：Rx=0Ry=0接下来，我们将讨论平面一般力系平衡方程的其他形式。
1.力矩方程：根据力矩的定义，力矩是力相对其中一点的偏转能力。
对于平面一般力系，可以选择任意一点O作为力矩参考点。
设力F作用在距离O点的位置向量r上，则力F的力矩的大小为，F，·，r，·sinθ，其中θ是力F相对r的夹角。
如果物体在该点处受力平衡，那么所有力的力矩之和必须为零。
∑M=0这个力矩方程除了描述力的力矩平衡之外，还可以用来求解力对物体的支点的约束力。
2.点力平衡方程：对于平面一般力系中的点力，可以用点力平衡方程表示。
设点力F的作用点为P(x,y)，则在x轴和y轴方向上的分力之和必须分别为零。
∑Fx=0∑Fy=0这个点力平衡方程可以用来求解力对物体的支点的约束力，以及物体上各个点的受力情况。
3.合力和合力矩均为零的方程：如果平面一般力系是平衡的，那么不仅受力的合力为零，而且受力的合力矩也必须为零。
合力矩为零的条件可以表达为：∑Mx=0∑My=0其中，∑Mx表示力相对于y轴的力矩之和，∑My表示力相对于x轴的力矩之和。
这个方程可以描述物体受力平衡时的旋转平衡。
总结起来，平面一般力系平衡方程的其他形式包括力矩方程、点力平衡方程和合力和合力矩为零的方程。
这些形式可以根据具体情况灵活应用，解决力学问题。
第九讲内容一、平面一般力系平衡方程的其他形式前面我们通过平面一般力系的平衡条件导出了平面一般力系平衡方程的基本形式，除了这种形式外，还可将平衡方程表示为二力矩形式及三力矩形式。
1．二力矩形式的平衡方程在力系作用面内任取两点A 、B 及X 轴，如图4－13所示，可以证明平面一般力系的平衡方程可改写成两个力矩方程和一个投影方程的形式，即⎪⎭⎪⎬⎫=∑=∑=∑000B A M M X (4－6) 式中X 轴不与A 、B 两点的连线垂直。
证明：首先将平面一般力系向A 点简化，一般可得到过A 点的一个力和一个力偶。
若0A =M 成立，则力系只能简化为通过A 点的合力R 或成平衡状态。
如果0B =∑M 又成立，说明R 必通过B 。
可见合力R 的作用线必为AB 连线。
又因0=∑X 成立，则0X =∑=X R ，即合力R 在X 轴上的投影为零，因AB 连线不垂直X 轴，合力R 亦不垂直于X 轴，由0X =R 可推得0=R 。
可见满足方程（4－6）的平面一般力系，若将其向A 点简化，其主矩和主矢都等于零，从而力系必为平衡力系。
2．三力矩形式的平衡方程在力系作用面内任意取三个不在一直线上的点A 、B 、C ，如图4－14所示，则力系的平衡方程可写为三个力矩方程形式，即⎪⎭⎪⎬⎫=∑=∑=∑000C B A M M M （4－7）式中，A 、B 、C 三点不在同一直线上。
同上面讨论一样，若0A =∑M 和0B =∑M 成立，则力系合成结果只能是通过A 、B 两点的一个力（图4－14）或者平衡。
如果0C =∑M 也成立，则合力必然通过C 点，而一个力不可能同时通过不在一直线上的三点，除非合力为零，0C =∑M 才能成立。
因此，力系必然是平衡力系。
综上所述，平面一般力系共有三种不同形式的平衡方程，即式（4－5）、式（4－6）、式（4－7），在解题时可以根据具体情况选取某一种形式。
无论采用哪种形式，都只能写出三个独立的平衡方程，求解三个未知数。
任何第四个方程都不是独立的，但可以利用这个方程来校核计算的结果。
【例4－7】 某屋架如图4－15（a ）所示，设左屋架及盖瓦共重kN 31=P ，右屋架受到风力及荷载作用，其合力kN 72=P ，2P 与BC 夹角为︒80，试求A 、B 支座的反力。
【解】 取整个屋架为研究对象，画其受力图，并选取坐标轴X 轴和Y 轴，如图4－15（b ）所示，列出三个平衡方程kN39.2342.0770cos 070cos 02A 2A =⨯=︒==︒-=∑P X P X X30tan 470cos 1270sin 416 0221B A =︒⨯⨯︒+⨯︒-⨯-⨯=∑P P P Y MkN 34.516577.342.07494.0712341630tan70cos470sin124221B=⨯⨯⨯-⨯⨯+⨯=︒⨯︒-︒+=PPPY30tan470cos470sin1216221AB=︒⨯⨯︒+⨯︒++-=∑PPPYMkN24.41630tan70cos470sin412221A=︒⨯︒+︒+=PPPY校核94.07334.524.470sin21BA=⨯--+=︒--+=∑PPYYY说明计算无误。
【例4－8】梁AC用三根支座链杆连接，受一力kN50=P作用，如图【解】取AC梁为研究对象，画其受力图，如图4－16（b）所示。
列平衡方程时，为避免解联立方程组，最好所列的方程中只有一个未知力，因此，取AR和BR的交点O１为矩心列平衡方程kN 2.376866.05045.0502660sin 460cos 2 0460sin 260cos 6 0C C O 1=⨯⨯+⨯⨯=︒+︒==⨯︒-⨯︒-⨯=∑P P R P P R M取B R 与C R 的交点O 2为矩心列平衡方程260sin 460cos 45cos 60A O 2=⨯︒-⨯︒+︒⨯-=∑P P R M kN99.216707.0)866.05025.0504(6)60sin 260cos 4(A =⨯⨯⨯+⨯⨯=︒+︒=P P R 取 060cos 45cos 45cos 0B A =︒-︒-︒=∑P R R XkN 37.13707.05.050707.099.2145cos 60cos 45cos A B -=⨯-⨯=︒︒-︒=P R R校核866.0502.37707.037.13707.099.2160sin 45sin 45sin C A =⨯-+⨯-⨯=︒-+︒+︒=∑P R R R Y B说明计算无误。
3．平面力系的特殊情况平面一般力系是平面力系的一般情况。
除前面讲的平面汇交力系，平面力偶系外，还有平面平行力系都可以看为平面一般力系的特殊情况，它们的平衡方程都可以从平面一般力系的平衡方程得到，现讨论如下。
（1）平面汇交力系对于平面汇交力系，可取力系的汇交点作为坐标的原点，图4－17(a)所示，因各力的作用线均通过坐标原点O ，各力对O 点的矩必为零，即恒有0O =∑M 。
因此，只剩下两个投影方程0 0=∑=∑Y X即为平面汇交力系的平衡方程。
（2）平面力偶系平面力偶系如图4－17(b)所示，因构成力偶的两个力在任何轴上的投影必为零，则恒有0=∑X 和0=∑Y ，只剩下第三个力矩方程，但因为力偶对某点的矩等于力偶矩，则力矩方程可改写为0O =∑m即平面力偶系的平衡方程。
（3）平面平行力系平面平行力系是指其各力作用线在同一平面上并相互平行的力系，如图4－17（Ｃ）所示，选OY 轴与力系中的各力平行，则各力在X 轴上的投影恒为零，则平衡方程只剩下两个独立的方程⎭⎬⎫=∑=∑00O M Y （4－8）若采用二力矩式（4－6），可得⎭⎬⎫=∑=∑00B A M M （4－9）式中A 、B 两点的连线不与各力作用线平行。
平面平行力系只有两个独立的平衡方程，只能求解两个未知量。
【例4－9】 图4－18所示为塔式起重机。
已知轨距m 4=b ，机身重kN 260=G ，其作用线到右轨的距离m 5.1=e ，起重机平衡重kN 80=Q ，其作用线到左轨的距离m 6=a ，荷载P 的作用线到右轨的距离m 12=l ，（1）试证明空载时（0=P 时）起重机时否会向左倾倒（2）求出起重机不向右倾倒的最大荷载P 。
【解】 以起重机为研究对象，作用于起重机上的力有主动力G 、P 、Q 及约束力A N 和B N ，它们组成一个平行力系（图4－18）。
（1）使起重机不向左倒的条件是0B ≥N ，当空载时，取0=P ，列平衡方程0)( 0B A =+-⋅+⋅=∑b e G b N a Q M[][]0kN 5.237680)45.1(26041)(1B >=⨯-+=⋅-+=a Qb e G b N 所以起重机不会向左倾倒（2） 使起重机不向右倾倒的条件是0A ≥N ，列平衡方程[]l P e G b a Q bN l P e G b N b a Q M ⋅-⋅-+==⋅-⋅-⋅-+=∑)(10)( 0A A B欲使0A ≥N ，则需0)(≥⋅-⋅-+l P e G b a Q[][]kN17.345.1260)46(80121)(1=⨯-+=⋅-+≤e G b a Q l P 当荷载kN 17.34≤P 时，起重机是稳定的。
二、物体系统的平衡前面研究了平面力系单个物体的平衡问题。
但是在工程结构中往往是由若干个物体通过一定的约束来组成一个系统。
这种系统称为物体系统。
例如，图示4－19（a ）所示的组合梁，就是由梁AC 和梁CD 通过铰C 连接，并支承在A 、B 、D 支座而组成的一个物体系统。
在一个物体系统中，一个物体的受力与其他物体是紧密相关的；整体受力又与局部紧密相关的。
物体系统的平衡是指组成系统的每一个物体及系统的整体都处于平衡状态。
在研究物体系统的平衡问题时，不仅要知道外界物体对这个系统的作用力，同时还应分析系统内部物体之间的相互作用力。
通常将系统以外的物体对这个系统的作用力称为外力，系统内各物体之间的相互作用力称为内力。
例如图4－19（b ）的组合梁的受力图，荷载及A 、B 、D 支座的反力就是外力，而在铰C 处左右两段梁之间的互相作用的力就是内力。
应当注意，外力和内力是相对的概念，是对一定的考察对象而言的，例如图4－19组合梁在铰C 处两段梁的相互作用力，对组合梁的整体来说，就是内力，而对左段梁或右段梁来说，就成为外力了。
当物体系统平衡时，组成该系统的每个物体都处于平衡状态，因而，对于每一个物体一般可写出三个独立的平衡方程。
如果该物体系统有n 个物体，而每个物体又都在平面一般力系作用下，则就有n 3个独立的平衡方程，可以求出n 3个未知量。
但是，如果系统中的物体受平面汇交力系或平面平行力系的作用，则独立的平衡方程将相应减少，而所能求的未知量数目也相应减少。
当整个系统中未知量的数目不超过独立的平衡方程数目，则未知量可由平衡方程全部求出，这样的问题称为静定问题。
当未知量的数目超过了独立平衡方程数目，则未知量由平衡方程就不能全部求出，这样的问题，则称为超静定问题，在静力学中，我们不考虑超静定问题。
在解答物体系统的平衡问题时，可以选取整个物体系统作为研究对象，也可以选取物体系统中某部分物体（一个物体或几个物体组合）作为研究对象，以建立平衡方程。
由于物体系统的未知量较多，应尽量避免从总体的联立方程组中解出，通常可选取整个系统为研究对象，看能否从中解出一或两个未知量，然后再分析每个物体的受力情况，判断选取哪个物体为研究对象，使之建立的平衡方程中包含的未知量少，以简化计算。
下面举例说明求解物体系统平衡问题的方法。
【例4－10】 组合梁受荷载如图4－20(a)所示。
已知kN,161=P kN 202=P ，m kN 8⋅=m ，梁自重不计，求支座A 、C 的反力。
【解】 组合梁由两段梁AB 和BC 组成，作用于每一个物体的力系都是平面一般力系，共有6个独立的平衡方程；而约束力的未知数也是6（A 处有三个，B 处有两个，C 处有1个）。
首先取整个梁为研究对象，受力图如图4－20（b ）所示。
kN1060cos 060cos 02A 2A =︒==︒-=∑P X P X X其余三个未知数A Y 、A m 和C R ，无论怎样选取投影轴和矩心，都无法求出其中任何一个，因此，必须将AB 梁和BC 梁分开考虑，现取BC 梁为研究对象，受力图如图4－20（c ）所示。
kN1060cos 060cos 02B 2B =︒==︒-=∑P X P X XkN66.8260sin 0160sin 2 02C 2B =︒==⨯︒-=∑P R P R M C kN66.860sin 060sin 02C B 2B C =︒+-==︒-+=∑P R Y P Y R Y再回到受图4－20（b ）kN98.655260sin 4 0260sin 45 0C 12A A 12C A =+-+︒==+-⨯-︒-=∑m R P P m m m P P R MkN66.2460sin 060sin 0C 21A 21C A =-︒+==︒--+=∑R P P Y P P R Y Y校核：对整个组合梁，列出866.82866.020111666.24398.65260sin 113-C 21A A B =-⨯+⨯⨯-⨯+⨯-=-+︒⨯-⨯+=∑mR P P Y m M 可见计算无误。
