04正五边形的作图方法

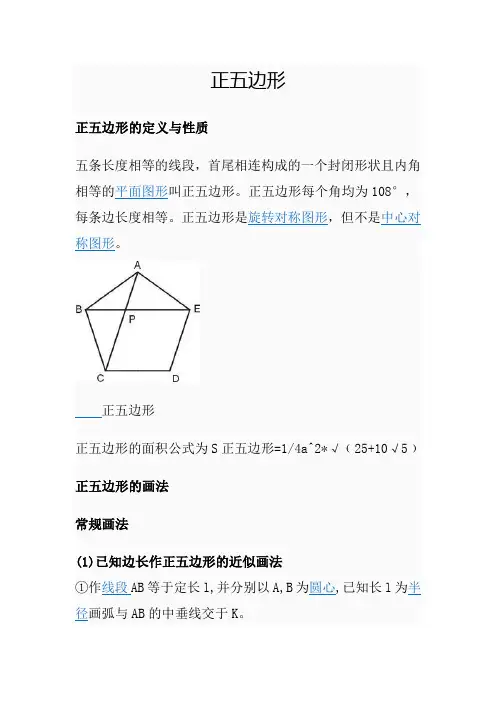
②取AB的2/3长度延长AK到C，使CK=2/3AB。

③以点C为圆心，已知边长AB为半径画弧，分别与前两弧相交于M，N。

④顺次连接A，B，N，C，M各点即近似作得所要求的正五边形。

(2)民间口诀画正五边形口诀介绍：“九五顶五九,八五两边分”。

画法:①画线段AB=20mm。

②作线段AB的垂直平分线l，垂足为G。

③在l上连续截取GH，HD，使 GH=9.5/5*10mm=19mm，HD=5.9/5*10mm=11.8mm。

④过H作EC⊥HG,在EC上截取HE=HC=8/5*10mm=16mm。

⑤连结DE，EA，AB，BC，CD。

五边形ABCDE就是边长为20mm的近似正五边形。

尺规作图画法理论依据：cos36°=(1+√5)/4正五边形 - 几何画板1. 在平面内作一圆，圆心为O；2. 在圆O上取一点A，连接AO并延长交圆O于另一点B；【假令|AB|=4】3. 过点O作CD⊥AB，交圆O于C、D两点；【此时|CD|=4】4. 作OB垂直平分线MN，交OB于E点，交圆O于M，N【此时|OE|=|BE|=2】5. 以点E为圆心，EC长为半径作弧，交BO延长线于点F；【此时|EC|=|EF|=√5】6. 以点B为圆心，BF长为半径作弧，交圆O分别于G、H两点；【此时|BF|=|EF|+|BE|=1+√5】【此时可知cos∠ABG=(|EF|+|BE|)/|AB|=(1+√5)/4=36°】【而∠AOG=2∠ABG=72°=360°/5(直径所对的圆周角)】【此时便得到了圆周上的五等分点的其中两个。

】7. 以点G为圆心，GA长为半径作弧，交圆O于P点；8. 以点H为圆心，HA长为半径作弧，交圆O于Q点；9. 连接AG、GP、PQ、QH、HA,则五边形AGPQH为正五边形。

圆内接正五边形圆内接正五边形的定义与性质圆内接正五边形指内接于圆的正五边形。

圆内接正五边形的每一条边相等（即圆的每一条弦相等），每个角均为108°，每个角在圆内所对的优弧相等。

正五边形的画法原理正五边形的画法什么是正五边形？正五边形是指五边形的五个边长度相等，五个内角也相等的特殊五边形。

它具有对称美和几何美，是艺术创作和数学研究中常用的形状之一。

如何画一个正五边形？方法一：利用直尺和圆规1.准备一张白纸和一支铅笔，以及一个有刻度的直尺和一个半径恰好为正五边形边长的圆规。

2.在白纸上选择一个点作为正五边形的中心点，并将其标记为A。

3.利用圆规，以点A为圆心，画一个半径为正五边形边长的圆，将圆的周围等分为五等分，标记为B、C、D、E、F。

4.用直尺连接点A和点B，点B和点C，点C和点D，点D和点E，点E和点F，分别得到正五边形的五个边。

5.擦除多余的线段和标记，得到一个完整的正五边形。

方法二：利用数学原理和投影仪1.准备一个投影仪和一块透明的图纸。

2.将投影仪调至平面模式，将透明图纸固定在投影仪上。

3.将投影仪的光源对准墙壁或纸张，使其正好投影一个完整的正五边形。

4.将投影在墙壁或纸张上的正五边形轮廓用铅笔描画出来，得到一个精确的正五边形。

正五边形的原理正五边形的画法基于以下原理：•正五边形的每个内角都是108°，即360°/5。

•圆规的半径为正五边形边长的一半。

•利用直尺和圆规的结合可以构造出正五边形的边。

•利用投影仪可以将正五边形的投影放大，方便描绘。

正五边形的原理基于几何学的知识和图形构造的方法，通过不同的工具和技巧，可以画出精确的正五边形。

结语正五边形是一种特殊的几何形状，它具有对称美和几何美。

通过了解正五边形的画法原理，我们可以更好地理解和应用正五边形，无论是在艺术创作还是数学研究上，都能够发挥重要的作用。

希望本文所介绍的正五边形的画法对您有所帮助！方法三：利用三角形的性质1.准备一张纸和一支铅笔。

2.在纸上选择一个点作为正五边形的中心点，并将其标记为A。

3.利用直尺，在点A的上方和下方各选择一个点，分别标记为B和C，使得AB=AC。

4.利用直尺连接点B和点C，得到线段BC。

民间口诀画正五边形的画法
我国民间相传有正五边形的近似画法：画法口诀是：“九五顶五九，八五分两边”。

根据这个口诀，画出一个边长为2cm的正五边形。

画法：
1、用点工具作出点A。

2、选取点A，单击变换菜单下的平移命令，打开平移对话框，选择按极坐标向量平移方式（在该选项上单击鼠标，使其出现√标记）。

3、在方向输入框中输入0，在数量输入框中输入2，单击确定按钮。

得到点B（如果作图中得到的默认名称与此不同，可用文本工具为其重新命名，以下同）。

4、用线段工具连结AB，选中它，用中点命令作出它的中点G。

5、选取线段AB，用度量菜单中的长度命令得到它的长度。

6、双击长度度量值，打开计算器，输入9．5、／、10、＊，再单击AB 长度值，按下确定按钮。

得到距离1；类似地将刚才表达式中的9．5分别换成5．9和8，得到距离2和距离3。

7、选中距离1，单击变换菜单下的标记距离命令，将其作为标记距离。

8、选取中点G，单击平移命令，选择极坐标向量平移方式，在方向输入框中输入90，数量选用按标记距离，按下确定按钮。

得到点H。

9、同样地，将距离2作为标记距离，用极坐标向量方式将H点向上平移（方向90），得到点D；将距离3作为标记距离，将H点向左平移（方向180）得到点E，将H点向右平移（方向0）得到点C（平移数量均用标记距离）。

10、用线段工具连结点BC、CD、DE、EA，就得到了一个近似的正五边形。

正五边形尺规作图方法赏析作者：谢俊峰来源：《数学大世界·上旬刊》2018年第11期尺规作图是起源于古希腊的数学课题。

历史上最先明确提出尺规限制的是希腊天文学家、数学家伊诺皮迪斯。

由于对尺规作图的限制，使得一些貌似简单的几何作图问题无法解决。

最著名的是古希腊最有影响力的四大数学学派之——巧辨学派提出的三大著名尺规作图问题：倍立方问题、化圆为方问题、三等分角，当然，这三个问题都已被证明不可能用尺规作图来解决。

尺规作图中有许多有趣的问题，其中作正多边形就是其中一种。

大家认为这是一个简单的问题，但在操作中我们知道，正四邊形、正五边形、正六边形都比较简单，但到正七边形、正九边形却遇到了很大的困难，最终解决这个问题的是伟大的数学家高斯，他给出了可用尺规作图的正多边形的条件：尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积。

本文提供正五边形的几种作图方法，供大家赏析。

一、已知圆的半径为r，求作圆的内接正五边形作法1：如图1，作圆O的任意半径OA1，A1B⊥OA1，并使得A1B=1/2OA1，连接BO，以B为圆心，删，为半径作弧截BO于点C，以O为圆心、0C为半径作弧截0A1于点M，以点A1起顺次截取等于0M的弦A1B2，A2B3，…，A10A1，将A2、A4、A6、A8、A10顺次连接，即为圆的内接正五边形。

作法2：如图2，作互相垂直的直径AM，BN，作0N的垂直平分线交ON于点E，以E为圆心、EA为半径作弧交OB于点F，从点A起顺次在圆上截取等于AF的弦，AA1、A1A2、A2A3、A3A4、A4A，顺次连接A、A1、A2、A3、A4、A，即得到正五边形。

作法3：如图3，任作圆O的半径OA，，过O点作OA1的垂线OB交圆O于点B，取OB的中点C，作∠OCA1的角平分线CD交于点D，过D点作DA2⊥OA1交圆O于点A2，从点A2起顺次在圆上截取等于A1A2的弦A2A3、A3A4、A4A5，顺次连接A1、A2. A3、A4.A5、A，即得到正五边形。

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆，设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心，MA为半径作圆，交OX于点N；5、以点A为圆心，AN为半径，在圆上连续截取等弧，使弦AB=BC=CD=DE=AN，则五边形ABCDE即为正五边形。

以上两种图形的作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的直规作图方法．确实，有的困难一些，有的容易一些．正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi （i为右下角标）＝22i（底数2指数2的i次幂）＋1 的数．费马的一个著名猜想是，当n≥3时，不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数，对于i＝0，1，2，3，4时，容易算出来相应的Fi：F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k（2的k次幂）或2k×p1×p2×…×ps，（1，2…s为右下角标）其中，p1，p2，…，ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正 13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而 3=F0．。

【初中数学】初中数学正五边形的公式定理大全【—正五边形公式定理】正五边形要领：正五边形每个角均为108°，每条边长度相等。

正五边形是旋转对称图形，但不是中心对称图形。

常规五角大楼正五边形的画法常规画法（1）已知边长规则五边形的近似作图方法①作线段ab等于定长l,并分别以a,b为圆心,已知长l为半径画弧与ab的中垂线交于k。

② 取2/3长度的AB，将AK延伸至C，使CK=2/3AB。

③以点c为圆心，已知边长ab为半径画弧，分别与前两弧相交于m，n。

④ 按顺序连接点a、B、N、C和m，即大致形成所需的规则五边形。

(2)民间口诀画正五边形公式简介：“九五”是前五个九年计划，而“八五”则分为两部分。

画法:① 绘制线段AB=20mm。

②作线段ab的垂直平分线l，垂足为g。

③ 连续截取L上的GH和HD，使GH=9.5/5*10mm=19mm，HD=5.9/5*10mm=11.8mm。

④过h作ec⊥hg,在ec上截取he=hc=8/5*10mm=16mm。

⑤ 连接De、EA、AB、BC、CD。

五边形abcde就是边长为20mm的近似正五边形。

尺规作图法1.作线段ab2.将AB剖面的垂直平分线设为hi，垂直底脚为h（基本图）3.以线段ab为一边,作正方形(不会作,看下面小步骤)（1）以点a为圆心，以适当的长度为半径，画一条弧，并在点c和D处与直线AB相交（清楚地看到，这是一条直线）。

(2)分别以点c、d为圆心，大于二分之一cd长为半径，画弧，两弧交于点e。

（3）通过点E绘制一条直线AE，并以点a为端点，在直线AE上截取线段AF=AB。

(4)以点f、b为圆心，线段ab长为半径，画弧，两弧交于点g。

（5）连接段FG和BG。

那么四边形abgf是正方形的。

4.继续。

以点h为圆心，线段hg长为半径，画弧，交射线hc于点j。

5.以a点和j点为圆心，以AB线的长度为半径绘制一条圆弧。

这两条弧在K点相交并连接akbk。

正五边形画高练习
简介
本文档旨在为读者提供研究如何画正五边形的指导和练方法。

正五边形是一种具有五个边长和五个内角相等的几何形状，它有许多实际应用，如建筑设计、艺术和数学等领域。

步骤
下面是画正五边形的步骤：
1. 准备一张空白纸和一支铅笔。

2. 在纸上选择一个起始点，并画出一个垂直的竖线作为第一条边。

3. 从这个点开始，向右旋转72度，然后画出第二条边。

4. 重复第3步，继续画出第三条、第四条和第五条边。

每条边都是72度旋转。

5. 最后一条边应该连接到起始点，形成一个闭合的正五边形。

注意事项
在练过程中，请注意以下几点：
- 保持手的稳定性，尽量画出直线和尖锐的角度。

- 使用铅笔轻轻地画出初步的线条，以便在需要时可以进行修改。

- 通过多次练来提高技巧，不必一次就画出完美的正五边形。

总结
通过按照上述步骤进行练，您将能够掌握画正五边形的技巧。

练是提高技能的关键，因此请务必耐心并持之以恒。

享受绘画过程，并展示您的创造力！。

画五边形的最简单方法
画五边形的最简单方法是使用直尺和圆规。

以下是步骤：
1. 用圆规画一个圆。

2. 用直尺连接圆的两个相邻点，这条线段将成为五边形的一条边。

3. 从这条线段的一个端点开始，用圆规测量出与圆相交的点，这个点将成为五边形的第二个顶点。

4. 用直尺连接这个新的顶点和之前画的线段的另一个端点，这条线段将成为五边形的第二条边。

5. 重复步骤3和4，直到五边形的所有顶点和边都画出来。

6. 检查五边形的每个角是否为108度，如果不是，则需要调整线段的长度或位置，直到所有角度都正确。

7. 最后，用铅笔或彩笔勾勒出五边形的轮廓。

正五边形几何作图法误差求证
摘要：本文运用计算机CAD技术对图形进行数值查询，求证正五边形几何作图法的误差数据，以方便企业现场生产。

关键词：正五边形几何作图法计算机CAD技术误差
正五边形几何作图法是广大技术工人多年以来依据经验不断摸索总结出来的一种作图方法，其具有方便快捷，不需要复杂数据计算的优点，在企业钣金放样现场生产工作中得到广泛应用。

然而正五边形几何作图法中常用的几种方法都不同程度地存在着一定的误差，现通过计算机CAD技术对图形进行数值查询，求证正五边形几何作图法的误差数据，以方便企业现场生产工作。

一、正五边形几何作图过程及误差
正五边形通过数值计算得：正五边形外形角为118°，圆心角为72°（假设圆周直径为2000mm，正五边形弦长为1175.570505mm）。

1.方法一（如图1所示）
图1
（1）分别以已知线段AB的端点A、B为圆心，线段AB长度为半径作弧，交线段AB的垂直平分线下延长线于H点。

（2）以H点为圆心，线段AB长度为半径作弧，两弧分别交前两弧于G、F点，与线段AB的垂直平分线交于O点。

（3）连接FO、GO并做线段FO、GO延长线，两延长线分别交两弧与E、C点。

（4）分别以E、C点为圆心，线段AB长度为半径作弧，两弧交于D点。

（5）连接A、B、C、D、E五点即为所求的五边形。

2.方法二（如图2所示）
图2
（1）作已知线段AB的垂直平分线，得线段AB的中点O。

（2）以线段AB的端点B点为圆心，以BO为半径作弧，交过B点所作线段AB的垂线于F点，连接AF。