平面应力状态

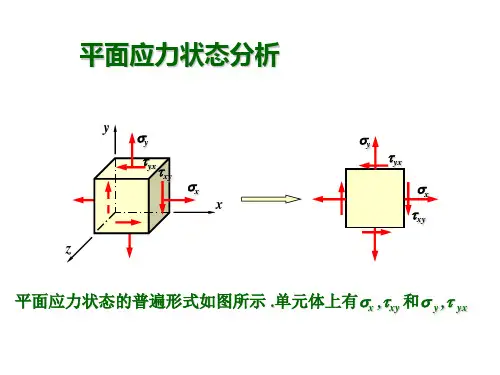
平面应力状态分析--主应力主平面详细推导老和尚小方丈（storylee_dut@）大连理工大学+哈尔滨电机厂有限责任公司平面应力状态有一个主应力为0，全部应力分量假设位于一个平面，鉴于市场上材料力学教材关于平面应力状态分析公式推导不尽详细，在此进行详细推导，为广大力学人士提供参考，敬请批评指正。

任意斜截面上的应力公式为：ατασσσσσα2sin 2cos 22xy yx y x --++=（1）ατασστα2cos 2sin 2xy yx +-=（2）式中，α为斜截面外法线n 与x 轴正向的夹角。

对于主平面方位的确定，根据主平面定义可知，主平面上的切应力为0，由（2）式得：02cos 2sin 2000=+-=ατασσταxy yx （3）即yx xyσστα--=22tan 0（4）方程（4）有两个解，主平面方位角0α与 900+α，说明两个主平面互为垂直关系。

将公式（3）的解回代公式（1），可得另外两个主应力，代数值较大的记为max σ，较小的记为min σ，则22max 22xy y x y x τσσσσσ+⎪⎪⎭⎫ ⎝⎛-++=（5）22min22xyy x y x τσσσσσ+⎪⎪⎭⎫ ⎝⎛--+=（6）关于公式（3）的解诸多材力教材没有此部分推导，本文列如下：对于方程yx xyσστα--=22tan 0更改等效形式002cos 22sin ασσταyx xy--=（7）添加方程12cos 2sin 0202=+αα（8）联立（7）、（8）求得：2220222cos xy y x y x τσσσσα+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-±=（9）222022sin xy y x xyτσστα+⎪⎪⎭⎫ ⎝⎛-=（10）注意（9）、（10）公式正负号的对应，再将（9）、（10）代入公式（3）推得主应力计算公式（5）、（6），至此，详细推导完成！。

1. 脆性断裂：断裂前，材料未发生明显的宏观塑性变形的断裂，或指断裂应力低于材料屈服强度的断裂2. 包申格效应：是指金属材料经预先加载产生少量塑性变形（残余应力小于4％），而后再同向加载，规定残余伸长应力（屈服强度、弹性极限）增加，反向加载，规定残余伸长（屈服强度、弹性极限）应力降低的现象。

3. 应力状态软性系数：应力状态中最大切应力和最大正应力的比值4. 刚度：在弹性变形范围内，构件抵抗变形的能力。

5.热疲劳：由周期变化的热应力或热应变引起的材料破坏称为热疲劳。

6.蠕变：材料在长时间的恒温、恒载荷作用下缓慢地产生塑性变形的现象。

7.疲劳强度：在指定疲劳寿命下，材料能承受的上限循环应力。

8.断裂韧度：裂纹失稳扩展的临界状态所对应的应力场强度因子称为材料的断裂韧度9.技术磁化：铁磁材料在外加磁场的作用下所产生的磁化称为技术磁化。

10.允带：电子可以具有的能级所组成的能带称为允带。

1. 韧性：是指材料在断裂前吸收塑性变形功和断裂功的能力。

4.松弛稳定性：材料抵抗应力松弛的能力称为松弛稳定性。

7.低温脆性：材料随着温度下降，脆性增加，当其低于某一温度时，材料由韧性状态变为脆性状态，这种现象为低温脆性。

8.解理断裂：材料在拉应力的作用下原于间结合破坏，沿一定的结晶学平面(即所谓“解理面”)劈开的断裂过程。

6. 破损安全：构件内部即使存在裂纹也不导致断裂的情况。

7.平面应力：只在一个平面内存在应力的现象。

10. △K th ：疲劳裂纹扩展的门槛值，表征材料阻止疲劳裂纹开始扩展的能力1. 解释形变强化的概念，并阐述其工程意义。

答：材料进入塑性变形阶段后，随着变形量增大，形变应力不断提高的现象称为形变强化。

（2分）形变强化是金属材料最重要的性质之一，其工程意义在于：1）形变强化可使材料或零件具有抵抗偶然过载的能力，阻止塑性变形的继续发展，保证材料安全。

2）形变强化是工程上强化材料的重要手段，尤其对于不能进行热处理强化的材料，形变强化成为提高其强度的非常重要的手段。

平面应力状态分析--几何法(1)平面应力状态分析--几何法(1)平面应力状态分析—几何法(1)cos 2sin 222sin 2cos 22x y x y xy x yxy αασσσσσατασστατα+-=+--=+一. 问题的提出mm Fq解析法22max 22min ()22()22x y x y xy x y x y xy σσσσστσσσσστ⎧+-=++⎪⎪⎨+-⎪=-+⎪⎩平面应力状态分析—几何法(1)22max 22min ()2()2x y xy x y xy σσττσσττ⎧-=+⎪⎪⎨-⎪=-+⎪⎩1tan2=2x y xyσσατ-02tan 2x x y τασσ=--平面应力状态分析—几何法(1)解析法优点：理论严谨，使用方便！缺点：公式太多，容易记错！有没有第二种方法呢？平面应力状态分析—几何法(1)二. 应力圆cos 2sin 2 22sin 2cos 22x y x y x x yx αασσσσσατασστατα+--=--=+过受力构件任一点处某斜截面(α方位角)上的应力计算公式可改写为：平面应力状态分析—几何法(1)消去α，得到：2222()()22x yx yxαασσσσσττ+--+=+上式是一个以σα和τα为变量的圆周方程。

当斜截面随方位角α变化时，其上的应力σα,τα在σ-τ直角坐标系内的轨迹是一个圆，称为莫尔应力圆(Mohr’s circle )。

平面应力状态分析—几何法(1)1. 圆心的坐标(,0)2x y C σσ+2. 圆的半径22()2x yxR σστ-=+所谓几何法，就是通过在σ-τ坐标系内画出应力圆来对受力构件内一点应力状态进行分析的方法。

位于σ轴上应力圆平面应力状态分析—几何法(1)三. 应力圆的做法1. 给定初始单元体，建立坐标系，选定比例尺。

标准的初始单元体平面应力状态分析—几何法(1)2. 量取OA= σx，AD= τxy，得D点；3. 量取OB= σy，BD′= τyx，得D′点；平面应力状态分析—几何法(1)4. 连接DD′两点的直线与 轴相交于C点；5. 以C为圆心，CD为半径作圆，该圆就是相应于单元体的应力圆。

平面应力和平面应变1． 平面应力在三维应力分布中，如果作下列假定无关与z 、、xy y x yz xz z τσσττσ0=== 1-1就得到了平面应力问题。

这种情况发生在薄板边界处受到平行于板面、并且沿厚度均匀分布的力作用的时候如图。

这时，在板的上下表面处，z σ、xz τ、yz τ为零（z 为板的法向），并认为沿着整个厚度方向它们也等到于零（因为厚度很小）。

应力状态只须用仅与x 、y 有关的x σ、y σ、xy τ来描述，称为平面应力情况。

此时，这三个应力分量与z 无关，即沿着板厚度保持不变。

平面应力问题的所有方程可以从相应的三维方程并结合式1-1得到：平衡方程 ⎪⎪⎭⎪⎪⎬⎫=+∂∂+∂∂=+∂∂+∂∂00y y xy x xy x f y x f y x σττσ 1-2 边界条件 ⎪⎭⎪⎬⎫+=+=--y xy xy x m l Y m l X σττσ 1-3 应变--位移方程 ⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂=∂∂=∂∂=x v y u y v x u xy y x γεε 1-4 应力--应变方程 ()()⎪⎭⎪⎬⎫=-=-=G E v E v xy xy x y y y x x τγσσεσσε 1-5 这里()v E G +=12是剪切模量，在结构的矩阵分析中，常把1-5式写成矩阵形式。

即()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧xy y x xy y x v v E τσσγεε1201011称对 1-6 或者，反之用应变表示应力，则有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧xy y x xy y x v v vE γεετσσ21010112称对 或记： {}[]{}εσD = 1-7其中： []⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--=21010112v v v E D 称对 1-8 协调方程 y x x y xy y x ∂∂∂=∂∂+∂∂γεε22222 1-9 此外，还必须注意下面两点：1） 在平面应力状态中0=z σ，而0≠z ε，事实上有()⎪⎪⎭⎪⎪⎬⎫==+-=00yz xzy x z E v γγσσε 2）平面应力假定下，方程式1-1是违背了某些协调条件的。