平面应力问题

试述平面应力问题和平面应变问题的特点。

平面应力问题和平面应变问题是固体力学中的两个重要概念，用于描述材料在二维平面内受力和变形的行为。

它们具有以下特点：
平面应力问题特点：
1.二维平面：平面应力问题假设材料在一个平面内受力，即只考虑材料在平
面内的应力分布，忽略沿垂直于该平面的应力分量。

2.平行应力：在平面应力问题中，只考虑平行于平面的应力分量，即沿着平
面的两个方向上的应力分量。

3.垂直应力：由于假设材料在平面外的应力分量为零，因此平面应力问题中
不考虑垂直于平面的应力分量。

4.线性弹性：平面应力问题通常基于线性弹性理论，即假设材料的应力-应
变关系是线性的。

平面应变问题特点：
1.二维平面：与平面应力问题类似，平面应变问题假设材料在一个平面内变
形，只考虑材料在平面内的应变分布，忽略垂直于该平面的应变分量。

2.平行应变：平面应变问题中，只考虑平行于平面的应变分量，即沿着平面
的两个方向上的应变分量。

3.垂直应变：与平面应力问题不同，平面应变问题中考虑垂直于平面的应变
分量。

4.线性弹性：平面应变问题通常基于线性弹性理论，假设材料的应力-应变
关系是线性的。

这些问题的特点使得对材料在二维平面内受力和变形行为进行简化和分析成为可能。

它们在工程学和材料科学中有广泛的应用，例如在结构力学、材料设计和应力分析中的应用。

平面应力问题和平面应变问题的异同点
平面应力和平面应变都是起源于简化空间问题而设定的概念。

平面应力：只在平面内有应力，与该面垂直方向的应力可忽略，例如薄板拉压问题。

平面应变：只在平面内有应变，与该面垂直方向的应变可忽略，例如水坝侧向水压问题。

具体说来：平面应力是指所有的应力都在一个平面内，如果平面是OXY平面，那么只有正应力σx，σy，剪应力τxy(它们都在一个平面内)，没有σz，τyz，τzx。

平面应变是指所有的应变都在一个平面内，同样如果平面是OXY平面，则只有正应变εx，εy和剪应变γxy，而没有εz，γyz，γzx。

举例说来：平面应变问题比如压力管道、水坝等，这类弹性体是具有很长的纵向轴的柱形物体，横截面大小和形状沿轴线长度不变；作用外力与纵向轴垂直，并且沿长度不变；柱体的两端受固定约束。

平面应力问题讨论的弹性体为薄板，薄壁厚度远远小于结构另外两个方向的尺度。

薄板的中面为平面，其所受外力，包括体力均平行于中面面内，并沿厚度方向不变。

弹性力学网上辅导 3平面问题的基本理论一、两类平面问题1.平面应力问题。

这类问题的条件是：弹性体是多厚度的薄板, 体力、面力和约束都只有xy 平面内的量，都不沿Z向变化；并且面力和约束只作用于板边，在板面上没有任何面力和约束的作用。

平面应力问题特征是：⑴由于板面上无面力和约束作用，以及薄板很薄，可以得出（（7 z , T ZX 和T xy）=0 （在平面域A内）。

因此，只有7x，7 y，T xy三个平面内的应力分量。

⑵由于物体形状和外力、约束沿z向均不变化，因此应力分量只是X，y两变量的函数。

以后还可从物理方程得出，应变分量也只是X，y的函数；而从几何方程积分求位移可见，位移与Z 有关。

归纳起来讲，所谓平面应力问题，就是只有平面应力分量（7 X，7 y和T xy）存在，且仅为X，y的函数的弹性力学问题。

例如，厚度较薄的浅梁和深梁，受上部荷载及自重的墙，以及有分缝的重力坝等，都属于平面应力问题，凡是符合上述这两点的问题，均属于平面应力问题。

2.平面应变问题这类问题的条件是：弹性体为常截面的很长柱体，体力、面力和约束条件与平面应力问题相似，只有xy平面内的体力、面力和约束的作用，且都不沿z向变化。

这个问题可以简化为平面应变问题。

平面应变问题特征是：⑴假想柱体为无限长时，则任一截面（z面）都是对称面，于是CD =0,只有平面位移分量u 和v 存在，因此，此问题可称为平面位移问题；同样由于对称性，c z =0和丫zx，丫zy=0 （相应的T zx，和T zy=0），只有平面应变分量£ x ，£y, T xy 存在，所以此问题又称为平面应变问题。

⑵由于截面形状、体力、面力及约束沿z向均不变，因此，它们只是X，y 的函数。

由此可见，所谓平面应变问题，就是只有平面应变分量（£ z , £ y和Txy ,）存在，且仅为x，y的函数的弹性力学问题。

进而可认为，凡是符合这两点的问题，也都属于平面应变问题。

平面应力问题和平面应变问题的基本方程中嘿，伙计们！今天我们要聊聊一个非常有趣的话题——平面应力问题和平面应变问题的基本方程。

别担心，我会用最简单的语言来解释这个话题，让你轻松理解。

让我们来看看什么是平面应力问题和平面应变问题吧。

平面应力问题，就是指在一个平面内，物体受到的力分布不均匀，导致物体内部产生应力。

而平面应变问题呢，就是指在一个平面内，物体的形状发生变化，导致物体内部产生应变。

这两个问题看似复杂，但其实它们都是由一个基本方程组成的。

这个基本方程就是什么呢？嘿嘿，让我慢慢告诉你。

这个方程叫做胡克定律，它是由英国科学家胡克在18世纪发现的。

胡克定律告诉我们，一个物体受到的应力与其形变成正比，与材料的弹性模量成反比。

换句话说，一个物体受到的应力越大，它的形变就越大；而材料的弹性模量越大，它所能承受的应力就越大。

那么，我们如何运用胡克定律来解决平面应力问题和平面应变问题呢？这里我就给大家举个例子吧。

假设我们有一个矩形板子，它的长度是L,宽度是W,材料是弹性模量为E的金属。

现在我们在板子的四个角上分别施加了40牛顿的力，让板子发生形变。

我们想要知道板子发生了多大的形变。

我们需要计算出板子受到的总应力。

因为我们在四个角上分别施加了40牛顿的力，所以总应力就是40 * 4 = 160牛顿。

接下来，我们要用胡克定律来计算板子的形变。

根据胡克定律，我们可以得到：$\Delta L = F times E \div (A * L)$$\Delta W = F \times E \div (A * W)$其中，$\Delta L$表示板子的长度变化，$\Delta W$表示板子的宽度变化，F表示施加在板子上的力，E表示板子的弹性模量，A表示板子的面积。

将已知的数据代入公式，我们就可以得到：$Delta L = 160 times E \div (4 * A) = 40E \div A$$\Delta W = 160 \times E div (4 * A) = 40E \div A$所以，板子的长度和宽度分别发生了$40E \div A$的形变。

平面应力举例
平面应力问题的一个典型例子是一块很薄的板，仅在板边上受到平行于板面的力和约束，且力的方向不随板的厚度变化而变化。

例如，手帕就可以被视为一个平面应力的例子，因为它很薄，只能承受绷紧的张力，而不能承受垂直于手帕的外力。

在这种情况下，手帕只受到沿其平面的应力作用，而垂直于手帕平面的应力可以忽略不计。

另一个例子是圆盘在边缘均布压力作用下的结构响应。

例如，一个半径为20mm，厚度为1mm的圆盘，在边缘施加10MPa的均布压强，这就是一个典型的平面应力问题。

在这种情况下，圆盘的变形和应力状态可以通过平面应力理论进行分析和计算。

这些例子都说明了平面应力问题的特点，即结构在某一方向（通常是厚度方向）的尺寸远小于其他两个方向，且外力作用平行于结构的主要平面，因此可以忽略垂直于该平面的应力分量，将问题简化为二维问题进行处理。

这种简化可以大大简化分析和计算过程，同时又能得到足够精确的结果，因此在工程实践中得到了广泛应用。

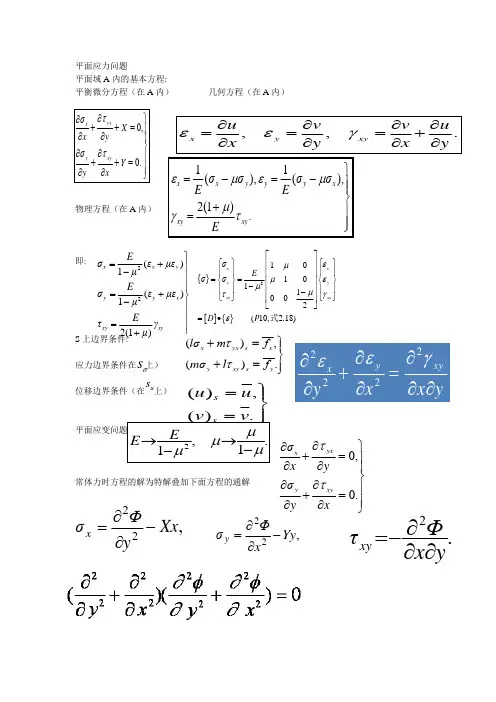
平面应力问题平面域A 内的基本方程:平衡微分方程（在A 内） 几何方程（在A 内）物理方程（在A 内）即: S 上边界条件:应力边界条件在 上）位移边界条件（在 上） 平面应变问题常体力时方程的解为特解叠加下面方程的通解0,0.yx x y xyσX x y σY y x ∂⎫∂++=⎪∂∂⎪⎬∂∂⎪++=⎪∂∂⎭ττ, , .x y xy u v v ux y x yεεγ∂∂∂∂===+∂∂∂∂11(),(),2(1).x x y y y x xy xy σσσσE E Eεμεμμγτ⎫=-=-⎪⎪⎬+⎪=⎪⎭22()1()(a)12(1)x x y y y x xy xyE σεμεμE σεμεμE τγμ⎫=+⎪-⎪⎪=+⎬-⎪⎪=⎪+⎭{}[]{}2101011002(10, 2.18)x x y y xy xy σE σσD P ⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪⎢⎥==⎨⎬⎨⎬⎢⎥-⎪⎪⎪⎪⎢⎥-⎩⎭⎩⎭⎢⎥⎣⎦=•εμμεμμτγε式(),().x yx s x y xy s y l σm f m σl f ττ⎫+=⎪⎬+=⎪⎭σs(),().s s u u v v ⎫=⎪⎬=⎪⎭us 2222y xy x y x x yεγε∂∂∂+=∂∂∂∂.1 ,12μμμμ-→-→E E 0,0.yx x y xyσx y σy x ∂⎫∂+=⎪∂∂⎪⎬∂∂⎪+=⎪∂∂⎭ττ22,y ΦσYy x∂=-∂.2yx Φτxy ∂∂∂-=22,x ΦσXx y∂=-∂二、基本假设 1、连续性假定假定物体是连续的。

因此，各物理量可用连续函数表示。

2、完全弹性假定a.完全弹性—外力取消，变形恢复，无残余变形。

b.线性弹性—应力与应变成正比。

即应力与应变关系可用胡克定律表示（物理线性）。

3、均匀性假定假定物体由同种材料组成,因此， E 、 μ等与位置 无关。

4、各向同性假定假定物体各向同性。

E 、μ与方向无关。

matlab平面应力问题例题平面应力问题是弹性力学中的基本问题之一，研究的是材料在平面内受到的力和应力分布。

在本文中，我们将讨论一个示例，以更好地理解该问题。

假设有一个光滑的平面，上面受到有限的力。

我们想要知道该平面上任意点的应力分布。

为了简化问题，我们假设该平面是无限大的，并且只受到一个均匀的力。

此外，我们还假设该平面的形状是矩形，其中一边的长度为a，另一边的长度为b。

首先，我们可以根据材料的弹性性质，使用胡克定律来描述该平面上的应力分布。

根据胡克定律，应力等于力除以面积。

由于该平面是矩形的，我们可以使用矩形的面积公式来计算面积，即面积等于a乘以b。

现在，我们需要考虑力的分布情况。

假设力沿着平面的一条边作用，我们可以将该力的大小表示为F。

为了简化计算，我们假设这个力是均匀分布在这条边上的，即单位长度上的力相等。

这意味着每个单位长度上的力为F/b。

根据胡克定律，我们可以计算出该平面上任意点的应力。

为了求解应力，我们需要确定力的作用点和该点到力所在边的距离。

假设我们选择平面上的一个点P，并且该点的坐标为(x, y)。

如果力是沿着边BC作用的，我们可以将P到BC的距离表示为y。

由于力是均匀分布的，我们可以根据该点到力所在边的距离来计算力的大小。

由于单位长度上力的大小为F/b，所以P点到力的大小可以表示为(F/b)·y。

现在，我们可以根据胡克定律来计算在点P处的应力。

根据公式，应力等于力除以面积。

力的大小为(F/b)·y，面积为a乘以b。

因此，P点处的应力可以表示为σ = [(F/b)·y] / (a·b)。

根据以上步骤，我们可以计算出该平面上任意点的应力。

这个结果可以用来描述材料在受到力作用时的应力分布情况。

通过将不同点的应力值绘制在平面上，我们可以获得应力分布的等值线图。

在这个例子中，我们讨论了一个简单的平面应力问题，并使用胡克定律计算出了平面上任意点的应力分布。

平面应变问题和平面应力问题的异同点1. 前言在我们讨论材料力学时，平面应变和应力这两个概念就像两个兄弟，性格各异却又密不可分。

想象一下，平面应变就像个爱静的书呆子，而平面应力则是那个热爱社交的朋友。

今天就来聊聊这两个家伙的异同，看看他们在我们生活中是怎么“打交道”的。

2. 平面应变问题2.1 定义与特征首先，平面应变问题指的是在某些条件下，材料在某个平面上的变形情况。

简单来说，就是我们常见的“拉伸”和“压缩”情景。

想象一下，像橡皮泥被捏扁了，表面看起来光滑，但内部却可能发生了复杂的变形。

在这种情况下，材料的某一方向的变形被假设为零，这样我们就能简单地处理问题。

2.2 应用场景说到应用，这平面应变可不简单！它常常出现在一些工程问题中，比如桥梁、隧道建设等，特别是在大规模的结构中。

想象一下，一个大桥的承重结构，所有的力都集中在某个平面上，这时应变问题就浮出水面了。

工程师们可得好好研究这个问题，才能保证桥梁的安全性。

3. 平面应力问题3.1 定义与特征转到平面应力问题，哎呀，这家伙可就热闹多了！它主要讨论在一个平面内的应力状态，简单来说，就是材料受到的各种力作用下的反应。

想象你在拥挤的地铁里被挤来挤去，那种“被压力包围”的感觉就是平面应力的典型表现。

这个时候，虽然我们也考虑了材料的厚度，但更关注的是在某个面上的力的分布。

3.2 应用场景在实际应用中，平面应力同样是不可或缺的。

很多时候，我们在设计零件，比如汽车车身或飞机机翼时，就会用到这个概念。

设计师们可得深思熟虑，确保在高速行驶时，这些材料能承受得住压力，绝不能让人有“毛毛的感觉”。

4. 异同点总结4.1 相似之处好啦，现在我们来看看这两个概念的相似之处。

首先，平面应变和应力都涉及到材料如何在外力作用下变形或反应，都是力学的基础。

其次，它们都为工程师提供了重要的分析工具，帮助他们设计出安全可靠的结构，真是一对“亲密无间”的兄弟。

4.2 不同之处不过，这两者的不同也挺明显的。

平面应力问题和平面应变问题举例下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一、平面应力问题。

在工程力学中，平面应力问题是一个经常遇到的问题。

平面应力问题名词解释平面应力问题啊，就像是一场二维世界里的力学小闹剧。

想象一下，应力就像是一群调皮的小怪兽，在一个平面这个小舞台上蹦跶。

你看，这个平面就像是一块超级薄的大饼，薄到几乎可以忽略它的厚度。

而应力呢，就像是那些在大饼上搞破坏的小捣蛋鬼。

它们可能会在这里拉拉扯扯，就像一群小孩子在抢一块美味的糖。

比如说，一个薄板受到外力的时候，平面应力问题就开始粉墨登场啦。

这就好比是一群蚂蚁在一张薄纸上搬运东西，而纸又不能太厚，不然就不是平面应力这个小天地里的事儿了。

在这个平面里，应力的分布就像是一幅奇怪的涂鸦。

有时候它们集中在某个角落，就像一群人都挤在一个小角落里看什么稀奇玩意儿。

而有时候又会分散开来，像是满天繁星，只不过这些星星不是在天上，而是在这个二维的平面里。

这平面应力问题啊，就像是一个微观世界里的战场。

应力的各个分量就像是不同的兵种，有的负责向前冲（正应力），有的则在旁边捣乱（剪应力）。

正应力就像是勇猛的战士，直来直往，而剪应力就像是狡猾的小贼，从侧面搞小动作。

要是从数学的角度看呢，平面应力问题就像是解一个充满谜题的迷宫。

那些应力公式就像是迷宫里的路线图，有时候你看着这些公式，就像看着天书一样，感觉自己像是走进了一个完全陌生的魔法世界，那些符号都在对你挤眉弄眼，似乎在嘲笑你不懂它们的奥秘。

而且啊，这个平面应力问题还特别爱跟工程师们玩捉迷藏。

工程师们就像侦探一样，要从各种蛛丝马迹里找到应力的真相。

他们得小心翼翼地分析这个薄平面的每一个角落，就像寻找宝藏一样，只不过这个宝藏不是金银珠宝，而是应力的分布规律。

如果把平面应力问题比作一场音乐会，那么应力就是那些演奏的音符。

不同的应力组合就像是不同的乐曲，有的和谐动听（应力分布均匀的时候），有的则是嘈杂刺耳（应力分布混乱的时候）。

总之呢，平面应力问题虽然听起来有点复杂，但是就像一个充满趣味的小世界。

只要你用心去探索，就会发现它像一个充满惊喜的魔法盒，每打开一次，都能找到不一样的乐趣。