高考数学复习《流程图》

高考数学复习点拨流程图的解答技巧流程图是由图形符号和文字说明构成的图示，流程图可以用来表示一些动态过程，它可直观、明确的表示动态过程的开始到结束的全部步骤。

下面通过实际例子看看写写流程图的技巧有：一、自上而下，逐步求精流程图一般按照从左到右、从上到下的顺序来写。

首先把一个复杂的大问题分解为若干相对独立的小问题，然后对应每个小问题再编写成相对独立的程序。

最后再把各个统一组装。

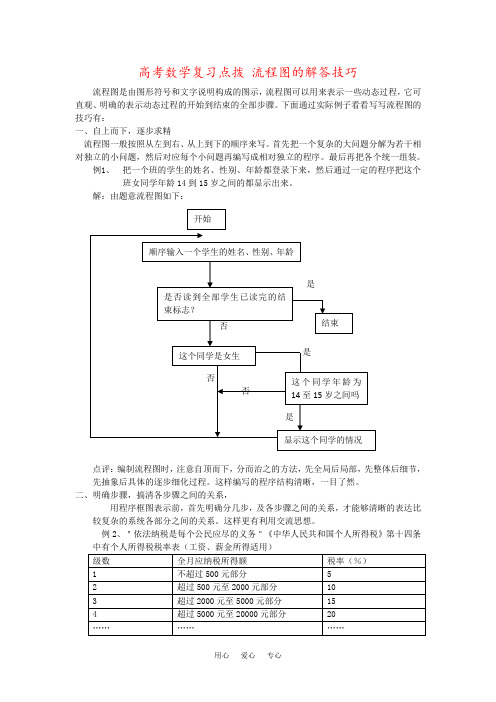
例1、把一个班的学生的姓名、性别、年龄都登录下来，然后通过一定的程序把这个班女同学年龄14到15岁之间的都显示出来。

解：由题意流程图如下：点评：编制流程图时，注意自顶而下，分而治之的方法，先全局后局部，先整体后细节，先抽象后具体的逐步细化过程。

这样编写的程序结构清晰，一目了然。

二、明确步骤，搞清各步骤之间的关系，用程序框图表示前，首先明确分几步，及各步骤之间的关系，才能够清晰的表达比较复杂的系统各部分之间的关系。

这样更有利用交流思想。

例2、＂依法纳税是每个公民应尽的义务＂《中华人民共和国个人所得税》第十四条中有个人所得税税率表（工资、薪金所得适用）如某人月工资、薪金收入1020元，减去800元后，应纳税所得额就是220元，应缴纳个人所得税11元，试编写一个流程图，输入某人月工资、薪金（)5000≤，输出这个人应缴纳的个人所得税。

分析：用x 表示月工资，用y 表示应纳的个人所得税。

当0<x ,800≤时，y ＝0。

当800<x ,1300≤时，y ＝（x －800）×5％＝0.05x －40当1300<x ,2800≤时，y ＝500×5％＋（x －1300）×10％＝0.1x －105当2800<x ,5000≤y=500×5％＋1500×10％＋（x －2800）×15％＝0.15x －245.点评：本题实际是求分段函数的值，多次用到条件语句，先通过求出解析式，搞清各部分的关系，再写程序框图就不难了。

高考数学知识点流程图高考数学是学生备战高考的重要一科，它涉及到许多关键的数学知识点和解题方法。

为了帮助考生更好地理解和掌握这些知识点，以下是一个高考数学知识点的流程图，旨在提供一个清晰的视觉呈现，方便考生回顾和巩固相关内容。

1. 数学思维导图在学习高考数学知识之前，我们首先了解数学思维导图的应用。

数学思维导图是一种图形化的表示方法，用于将数学概念和思维过程连系起来。

它可以帮助我们更好地理解和应用数学知识点。

2. 代数知识点代数是高考数学的基础，包括代数方程、函数和不等式等。

在流程图中，我们可以看到不同的代数知识点之间的联系。

比如，方程可以通过运算和移项来解决，而函数则可以通过图像和表格的呈现来分析和解决问题。

3. 几何知识点几何是高考数学中的另一个重要组成部分。

它涉及到平面几何和立体几何等内容。

流程图中展示了几何知识点之间的关系，如图形的性质和相似性的判断准则，以及三角形和圆的属性等。

通过学习和掌握这些知识点，我们可以更好地理解和解决与几何相关的问题。

4. 概率与统计知识点概率与统计是高考数学中的一部分，它包括了概率和统计的基本概念和运算方法。

在流程图中，我们可以看到概率和统计知识点之间的联系，如事件的概率计算、随机变量的分析和统计数据的处理等。

通过熟练掌握这些知识点，我们可以更好地理解和应用概率与统计学在实际问题中的解决方法。

5. 导数与微积分知识点导数与微积分是高考数学的一大难点，它涉及到函数的变化率和极值等内容。

在流程图中，我们可以看到导数和微积分知识点之间的联系，如导数的求解方法和微分应用等。

这些知识点对于理解函数的性质和解决最优化问题至关重要。

通过以上的流程图，我们可以清晰地了解和回顾高考数学的各个知识点之间的联系和应用。

希望考生们能够认真学习和掌握这些知识点，合理利用这个流程图，提高解题的能力和效率。

最后，祝愿所有参加高考的考生能够取得优异的成绩，实现自己的理想目标！。

数学·选修1－2(人教A版)4．1流程图►达标训练1．下列说法中正确的是()A．流程图只有1 个起点和1 个终点B．程序框图只有1 个起点和1 个终点C．工序图只有1 个起点和1 个终点D．以上都不对答案：B2．下列关于逻辑结构与流程图的说法中正确的是() A．一个流程图一定会有顺序结构B．一个流程图一定含有条件结构C．一个流程图一定含有循环结构D．以上说法都不对答案：A3．按照下面的流程图，则可得到()A．2,3,4,5,6 B．2,4,6,8,10C．1,2,4,8,16 D．2,4,8,16,32解析：流程图的第一步工作向下依次得到2,4,8,16,32.故选D. 答案：D4．某人早晨起床后泡茶的过程可以用流程图表示为按照这样的安排，总耗时数应为()A．18 min B．8 minC．23 min D．17 min解析：总耗时为2＋15＋1＝18(min)，故选A.答案：A5．下图给出的是计算12＋14＋16＋…＋120的值的一个程序框图，其中判断框内应填入的条件是()A．i>10? B．i<10?C．i>20? D．i<20?答案：A6．(2013·茂名一模)某程序框图如下图所示，该程序运行后，输出的x值为31，则a等于()A．0 B．1C．2 D．3答案：D►素能提高1．(2013·广东卷)执行如下图所示的程序框图，若输入n的值为3，则输入s的值是()A．1 B．2 C．4 D．7答案：C2．某成品的组装工序图如下，箭头上的数字表示组装过程中所需要的时间(小时)，不同车间可同时工作，同一车间不能同时做两种或两种以上的工作，则组装该产品所需要的最短时间是()A．11 B．13 C．15 D．17解析：由于从A出发的三道工序不能同时进行，经过观察可知：从A出发的三道工序必须按照先A→B，然后A→C，再A→E的次序，做好后到D(或E)再到F，最后到G，能完成任务且组装时间最短．故所需的最短时间为2＋3＋2＋4＋2＋2＝15(小时)．故选C.答案：C3．(2013·山东卷)执行两次如图所示的程序框图，若第一次输入的a值为－1.2，第二次输入的a值为1.2，则第一次、第二次输出的a值分别为()A．0.2,0.2 B．0.2,0.8C．0.8,0.2 D．0.8,0.8解析：执行程序框图，第一次输入a＝－1.2，－1.2＜0，a＝－0.2，－0.2＜0，a＝0.8,0.8＞0,0.8＜1，故输出a＝0.8；第二次输入a ＝1.2,1.2＞0,1.2＞1，a＝0.2,0.2＜1，故输出a＝0.2.故选C.答案：C4．(2014·惠州二模)如图所示，程序框图(算法流程图)的输出结果为________．答案：11 125．如下图，程序框图输出的函数f(x)＝________，值域是________．答案：⎩⎪⎨⎪⎧x 2－x ，x ＜x 2－x ，x ，x ≥x 2－x 或⎩⎪⎨⎪⎧x 2－x ，x ＞2或x ＜0，x ，0≤x ≤2.[0，＋∞)6．阅读下图所示的程序框图，运行相应的程序，输出的结果T ＝________.答案：307．某市新年第一个月前10天监测到空气污染指数如下表所示(主要污染物为可吸入颗粒物，第i天监测得到的数据记为ai)：在对上述数据的分析中，一部分计算见下图所示的算法流程图，则这10个数据的平均数a－＝________，输出的S值是________．答案：60 3.48．执行下面框图所描述的算法程序，记输出的一列数依次为a1，a2，…，a n，n∈N*，n≤2 012.(注：框图中的赋值符号“＝”也可以写成“←”或“：＝”)(1)若输入λ＝2，写出输出结果；(2)若输入λ＝2，令bn ＝1a n －1，证明{bn }是等差数列，并写出数列{a n }的通项公式；(3)若输入λ＝52，令c n ＝2a n －1a n －2，T ＝c 1＋2c 2＋3c 3＋…＋2 012c 2012.求证：T <89.解析：(1)输出结果为0，22.(2)当λ＝2时，b n ＋1－b n ＝1a n ＋1－1－1a n －1＝112－a n－1－1a n －1＝2－a n a n －1－1a n －1＝－1(常数)，n ∈N *，n ≤2 012. 所以，{b n }是首项b 1＝－1，公差d ＝－1的等差数列．故b n ＝－n ，1a n －1＝－n ，数列{a n }的通项公式为a n ＝1－1n ，n ∈N *，n ≤2 012.(3)当λ＝52时，a n ＋1＝152－a n ，c n ＝2a n －1a n －2，c n ＋1c n ＝2a n ＋1－1a n ＋1－22a n －1a n －2＝252－a n －1152－a n－22a n －1a n －2＝14·2a n －1a n －22a n －1a n －2＝14.∴{c n }是以12为首项，14为公比的等比数列．c n ＝12n-1⎛⎫ ⎪⎝⎭14＝2n⎛⎫ ⎪⎝⎭14. T n ＝c 1＋2c 2＋3c 3＋…＋n ·c n＝2⎝ ⎛⎭⎪⎫14＋42⎛⎫ ⎪⎝⎭14＋63⎛⎫ ⎪⎝⎭14＋…＋2n n⎛⎫ ⎪⎝⎭14 14T n＝22⎛⎫ ⎪⎝⎭14＋43⎛⎫ ⎪⎝⎭14＋64⎛⎫ ⎪⎝⎭14＋…＋2n n+1⎛⎫ ⎪⎝⎭14，两式作差得 ⎝ ⎛⎭⎪⎫1－14T n ＝2⎝ ⎛⎭⎪⎫14＋22⎛⎫ ⎪⎝⎭14＋23⎛⎫ ⎪⎝⎭14＋24⎛⎫ ⎪⎝⎭14＋ (2)⎛⎫ ⎪⎝⎭14－2n n+1⎛⎫ ⎪⎝⎭14. 即34T n ＝2·⎝ ⎛⎭⎪⎫14⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫14n 1－14－2n ⎝ ⎛⎭⎪⎫14n ＋1＝23⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫14n －2n ⎝ ⎛⎭⎪⎫14n ＋1.∴T n ＝89⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎛⎫ ⎪⎝⎭n114－8n 3n+1⎛⎫ ⎪⎝⎭14＝89－89n⎛⎫⎪⎝⎭14－8n 3n1⎛⎫⎪⎝⎭14.当n ＝2 012时， T ＝89－892 012⎛⎫ ⎪⎝⎭14－83·2 012· 2 013⎛⎫ ⎪⎝⎭14<89.►品味高考1．(2013·江西卷)阅读如下程序框图，如果输出i ＝4，那么空白的判断框中应填入的条件是( )A ．S ＜8B ．S ＜9C ．S ＜10D ．S ＜11解析：由框图及输出i ＝4可知循环应为：i ＝2，S ＝5；i ＝3，S ＝8；i ＝4，S ＝9，输出i ＝4，所以应填入的条件是S ＜9，故选B.答案：B2．(2013·浙江卷)若某程序框图如图所示，则该程序运行后输出的值等于________．解析：第一步，S ＝1＋12＝32，k ＝2； 第二步，S ＝32＋12×3＝53，k ＝3；第三步，S＝53＋13×4＝74，k＝4；第四步，S＝74＋14×5＝95，k＝5，结束循环．输出S＝95.答案：9 53．(2013·湖北卷)阅读如图所示的程序框图，运行相应的程序．若输入m的值为2，则输出的结果i＝________.解析：i＝1，A＝2，B＝1→i＝2，A＝4，B＝2→i＝3，A＝8，B ＝6→i＝4，A＝16，B＝24，输出i＝4.答案：4。

感悟流程图在我们所介绍的流程图内， 每一个框代表一道工序， 流程线则表示两相邻工序之间的连接关系， 这是一个有向线， 其方向用它上边的箭头标示， 用以指示工序进展的方向。

明显，在工序流程图上不同意出现几道工序首尾相接的圈图或循环回路，自然对每一道工序还能够再细分， 还能够画出更精美的兼顾图， 这一点 完整近似于算法的流程图表示：自顶向下，逐渐细化。

例 1 请设计输出两点连线斜率的程序框图。

剖析：平面上两点 P 1 x 1, y 1 、 P 2 x 2 , y 2 ，若 x 1 x 2 ，则直线 P 1 P 2 的斜率不存在；若 x 1 x 2 ，则直线 PP 12 的斜率为 ky 2 y1 。

x 2 x 1分析：程序框图如图 1 所示：开始输入 x 1 , y 1, x 2 , y 2是x 1 x 2 ?否ky 2y1x 2 x 1斜率不存在输出 k结束 图 1评注：解决直线中的相关问题，大多采纳公式法，先赋值，再运算，再输出结果。

练习：已知三个数，设计一个程序框图，求它们中的最大数。

答案：程序框图如图 2 所示：开始输入实数 a 、b、 c是a b ?否b a是c b ?否输出 c输出 b结束图 2例 2 要想检查学生在某个敏感问题上能否愿意与父亲母亲坦诚沟通，不太容易。

由于这涉及到个人的隐私权，一般的问卷回受到拒绝。

假如检查者把检查的方式设计好，即保护了学生的隐私权，又能获取有效的检查数据。

你能设计出一份该社会检查工作的流程图吗？剖析：第一步：设计无记名问卷格式以下：务请配合，严格做到；要求学号是奇数者回答下列问题 A ，不然回答下列问题B 。

答案栏问题问题 A ：你的学好是奇数吗？问题 B：在问题上你不肯意与父亲母亲坦诚沟通吗？（1）不要写出你的姓名和学号；（2）不要说出你回答的是哪个问题；注意事项（3）要真切地回答下列问题；（4）不论回答哪个问题答案都写在同一个答案栏内；（5）在答案栏内画“√”表示“是” ，画“×”表示“不是”。