重力模型标定方法及比较分析.kdh
- 格式:pdf
- 大小:98.02 KB
- 文档页数:4

重力加速度几种测量方法的比较引言:重力加速度是物理学中的一个十分重要的物理量,在地面上不同的地区,重力加速度g值不相同,它是由物体所在地区的纬度、海拔等因素决定,随着地球纬度和海拔高度的变化而变化,准确地确定它的量值,无论从理论上、还是科研上、生产上以及军事上都有极其重大的意义。
测量重力加速度的方法有很多,我所要做的就是通过学习前人的理论知识,经过思考,在现有的实验室条件下,进行实验,做出归纳和总结,提出自己的看法与体会。
且实验方法虽然多,但有的测量仪器的精确度受环境因素的影响比较大,不是每种方法都适用,所以有必要对测量方法进行研究,找出一种适合测量本地重力加速度的方法。
一、重力加速度的测量方法(一)用自由落体法测量重力加速度1.实验仪器:自由落体装置(如图一),数字毫秒计,光电门(两个),铁球。
图一自由落体装置2.实验原理、步骤、注意事项实验原理:设光电门A 、B 间的距离为s ,球下落到A 门时的速度为0v ,通过A 、B 间的时间为t ,则成立:2/20gt t v s += (1)两边除以t ,得:2//0gt v t s += (2)设t x =,t s y /=,则:2/0gx v y += (3)这是一直线方程,当测出若干不同s 的t 值,用t x =和t s y /=进行直线拟合,设所得斜率为b ,则由2/g b =可求出g ,b g 2=(4) 实验步骤:(1)调节实验装置的支架,使立柱为铅直,再使落球能通过A 门B 门的中点。
(2)测量A 、B 两光电门之间的距离s 。
(3)测量时间t 。
(4)计算各组的x ,y 值,用最小二乘法做直线拟合,求出斜率b 及其标准偏差b S 、)(b u (注意:在取b 的时,由于立柱调整不完善,落球中心未通过光电门的中点,立柱上米尺的误差均给s 值引入误差,也是b 的不确定度来源,一般此项不确定度(B 类评定)较小,可略去不计,所以b S b u =)()。

重力模型及解释及系数计算方法9、简述交通分布的重力模型的基本原理及其计算过程:重力分布模型仿效牛顿万有引力定律,认为交通小区间的交通量与交通小区各自的交通发生量和吸引量成广义的正比关系,而与交通小区间的交通阻抗(距离、时间、费用)成广义的反比。
重力分布模型是一个非常有用的交通分布模型,它适用于运输网络出现较大变化时的未来交通出行分布预测。
但该模型应用时,需要标定模型的参数。
重力模型(gravity model)是一种最常用的方法,它根据牛顿的万有引力定律,即两物体间的引力与两物体的质量之积成正比,而与它们之间距离的平方成反比类推而成。
重力模型考虑了两交通小区间的吸引强度与吸引阻力,认为两交通小区之间的出行吸引与两交通小区的出行发生、吸引量成正比,与交通小区间的交通阻抗成反比。
重力模型直观上容易理解,预测考虑的因素比较全面,尤其是强调了局部与整体之间的相互作用,比较切合实际,即没有完整的O-D表,也能用O-D矩阵(只要能标定a)预测。
重力模型的一个致命缺点是短程O-D分布偏大,尤其是区内出行,在预测时必须给予注意。
下式为Casey(1955)提出的重力模型。
其中,:i,j小区的人口;d为i,j小区间的距离,α为系数。
上式的约束条件为:s.t.同时满足守恒条件的α是不存在的,因此,将重力模型修改如下:其中,为交通阻抗函数。
交通阻抗函数的几种形式:指数函数:(1)幂函数:(2)组合函数:(3)为参数。
单约束型B.P.R.模型其中,调整系数。
发生侧得到保证,即:以下以幂指数交通阻抗函数为例介绍其计算方法:第1步令m=0,m为计算次数。
第2步给出n(可以用最小二乘法求出)。
第3步令第4步求出第5步收敛判定。
若下式满足,则结束计算;反之,令m+1=m,返回第2步重复计算。
,作业:按上次作业给出的现状OD表和将来生成、发生与吸引交通量,利用下式重力模型和弗拉塔算法,求出将来OD表。
收敛标准。
重力模型:其中,,,。

重力场标定引言:重力场标定是一项重要的科学研究,它关乎我们对于地球和宇宙的认知。
在这篇文章中,我将以人类视角出发,结合自己的感悟,探讨重力场标定的意义和影响。
第一部分:重力场的奇妙世界重力场是我们周围无处不在的力量,它让我们紧紧地与地球相连。
站在地面上,我们感受到的稳固感,正是来自于这个庞大而又神奇的重力场。
每当我仰望星空时,我不禁沉思:重力场究竟是如何形成的?它是如何影响着我们的生活?第二部分:重力场标定的重要性重力场标定是科学家们努力追求的目标。
通过精确测量和标定地球的重力场,我们可以更好地理解地球的物理特性和构成,从而为地球科学研究提供重要的依据。
此外,重力场标定也对于导航、地震监测等领域具有重要意义。
准确的重力场数据不仅可以提高导航系统的精度,还能帮助我们更好地预测和监测地震活动。
第三部分:重力场标定的挑战与方法重力场标定并非易事,因为地球重力场的分布并不均匀,同时受到地壳构造和大气压力等因素的影响。
为了解决这些挑战,科学家们采用了多种方法,如重力测量仪器的研发和使用,通过多点观测和数据处理等手段来提高测量精度,从而更准确地标定重力场。
第四部分:重力场标定的人类探索重力场标定的研究需要科学家们勇于探索和创新的精神。
他们通过不断改进仪器、开展实地观测和数据分析,努力揭示重力场背后的奥秘。
正是因为他们的努力,我们才能更加深入地了解地球和宇宙的本质。
结语:重力场标定是一项重要的科学研究,它关乎我们对于地球和宇宙的认知。
通过准确测量和标定重力场,我们可以更好地理解和探索地球的物理特性,为导航、地震监测等领域提供重要的支持。
让我们一起向那些为重力场标定做出贡献的科学家们致敬,他们的努力将继续推动人类对宇宙的探索和发现。



重力物理题型的解题技巧分析在物理学中,重力是一个非常重要的概念和力量。
它贯穿于整个宇宙万物,影响着我们日常生活中的许多现象和事件。
掌握重力物理题型的解题技巧,对于理解和应用重力力学的原理至关重要。
本文将对重力物理题型的解题技巧进行深入分析,并探讨其中的一些难点。
首先,我们需要了解重力的基本概念。
重力是地球或其他天体对物体产生的吸引力。
它与物体的质量和距离有关。
了解这个基本概念是解决重力物理题型的第一步。
在解题时,我们需要考虑物体的质量以及与其他物体的距离。
其次,我们需要掌握解决重力物理题目的常用公式。
重力的计算公式为F=mg,其中F表示重力的大小,m表示物体的质量,g表示重力加速度。
这是一个常用的公式,通过它我们可以计算物体所受的重力大小。
当处理一个重力物理问题时,我们还需要考虑施加力的方向。
重力是一个向下的力,即使我们在题目中看不到明确的方向指示,我们也应该默认重力是向下的。
在处理问题时,正确地识别方向是解决问题的关键。
在解决重力物理问题时,有时我们需要分解重力。
分解重力是根据物体所在的平面和角度来计算重力的水平和垂直分力。
这一步骤便于我们更好地分析问题并找到解决问题的方案。
例如,当一个物体斜靠在一个斜面上时,我们可以将重力分解为垂直向下的分力和平行于斜面的分力。
在解决一些较为复杂的重力物理问题时,我们还需要考虑其他力的存在和相互作用。
例如,当一个物体同时受到重力和摩擦力的作用时,我们需要根据具体情况综合考虑它们之间的相互关系,并运用合适的公式来计算结果。
在解决重力物理问题时,我们还需要注意单位的转换。
重力的单位通常是牛顿(N),质量的单位是千克(kg),而重力加速度的单位是米/秒²。
如果题目中给出的数值不是以正确的单位表示,我们需要进行适当的单位转换,以确保我们的计算是准确的。
最后,我们还需要注意使用适当的图示和图像来解决重力物理问题。
绘制示意图和自由体图可以帮助我们更好地理解问题,并确定所需的变量和未知量。


重力模型标定方法的分析及应用
张兰;彭国雄
【期刊名称】《交通科技与经济》
【年(卷),期】2009(011)001
【摘要】介绍双约束重力模型参数标定的方法,并以西部某一新城区居民出行分布为例,详细给出参数标定的实现过程.表明此方法操作简单,在实际交通规划的出行分布预测阶段,具有一定参考价值.
【总页数】3页(P106-108)
【作者】张兰;彭国雄
【作者单位】同济大学交通运输工程学院,上海,201804;同济大学交通运输工程学院,上海,201804
【正文语种】中文
【中图分类】U491.112
【相关文献】
1.重力模型标定方法及分析 [J], 季凯
2.重力模型标定方法及比较分析 [J], 谢香君
3.重力模型标定方法及应用研究 [J], 褚琴;陈绍宽
4.空间重力模型标定方法与使用范围的研究 [J], 都国报;廖勇;郭倩倩
5.基于出行时空分布的重力模型标定方法研究 [J], 朱亮;王元庆;周荣
因版权原因,仅展示原文概要,查看原文内容请购买。


四种重力模型比较朱学毅【期刊名称】《舰船导航》【年(卷),期】2001(000)002【摘要】惯导系统必须利用有效的重力模型,以便精确地构造重力方程式。
本文比较了四种常用的重力模型,并且总结了它们之间的主要区别,为了使比较具有一致性,本文使用了WGS-84参数,并且把重力分量转换到参考椭球面上的本地导航系(东,北,天)。
下面分别描述这四种重力模型(按照其精度和/或有效性递增的顺序):(1)低伟度重力模型是标准重力矢量的一种近似。
当以导航坐标系表示时,其水平分量相对于椭球切面的水平分量定义为零。
(2)J2重力模型使用了标准重力势能的近假(它可以描述为无数个球面谐波数列),并且在以地球中心为固定原点的坐标系(BCEF)中生成重力矢量,此后这些ECEF分量被转换到本地导航坐标系中,其中子乖平面中的重力分量在椭球表面或其上方不为零。
重力与经度无关。
(3)标准重力模型产生了一个垂直于参考椭球面的重力矢量(根据定义);在椭球面上方,重力矢量有一个非零的北向分量。
重力矢量作为标准重力势能的梯度,是与经度无关的。
(4)一般重力近似模型使用了与实际重力势能近似的多项式(它表示为无穷项的两倍和),重力在三个方面上的分量在椭球表面上或其上方均不为零。
这个重力模型产生的重力矢量的各分量与经度有关。
在文章的开始列出了符号的意义,随后介绍了重力势能和标准重力势能概念。
根据不同的经度,纬度和海拔高度对四种重力模型中的重力矢量方向进行了对比(关于参考椭球),同时还检查了重力分量与坐标系的关系。
【总页数】7页(P29-35)【作者】朱学毅【作者单位】无【正文语种】中文【中图分类】U666.12【相关文献】1.EGM96,WDM94和GPM98CR高阶地球重力场模型表示深圳局部重力场的比较与评价2.重力场模型研究进展及最新重力位模型精度比较分析3.GRACE RL06与RL05时变重力场模型数据初步比较分析4.多类地球重力场模型的高程异常精度比较5.几种卫星测高海洋重力场模型精度比较分析因版权原因,仅展示原文概要,查看原文内容请购买。
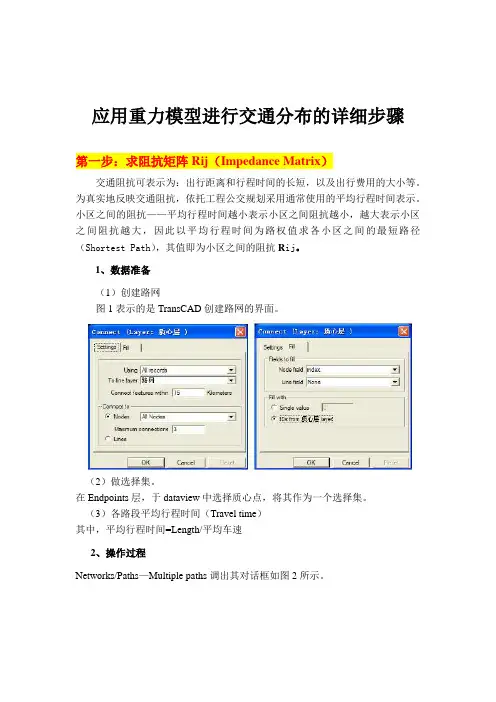
应用重力模型进行交通分布的详细步骤第一步:求阻抗矩阵Rij(Impedance Matrix)交通阻抗可表示为:出行距离和行程时间的长短,以及出行费用的大小等。
为真实地反映交通阻抗,依托工程公交规划采用通常使用的平均行程时间表示。
小区之间的阻抗——平均行程时间越小表示小区之间阻抗越小,越大表示小区之间阻抗越大,因此以平均行程时间为路权值求各小区之间的最短路径(Shortest Path),其值即为小区之间的阻抗R ij。
1、数据准备(1)创建路网图1表示的是TransCAD创建路网的界面。
(2)做选择集。
在Endpoints层,于dataview中选择质心点,将其作为一个选择集。
(3)各路段平均行程时间(Travel time)其中,平均行程时间=Length/平均车速2、操作过程Networks/Paths—Multiple paths调出其对话框如图2所示。
3、运行结果(即为阻抗矩阵),如图3所示。
第二步:重力模型标定(校准)(Gravity Mode Calibration)1、数据准备(1)公交基础OD矩阵。
(2)阻抗矩阵(Shortest Paths),如图3所示。
重力模型标定(校准)(Gravity Mode Calibration)数据准备:基年OD矩阵的索引(质心层质心ID)与最短路径矩阵的索引(路网节点层质心ID)不匹配,并且因为下面将在路网节点层上操作,因此必须使基年OD 索引与最短路径矩阵的索引相一致,以使两表数据相对应(转换为“质心ID”)。
操作方法:按其对话框4示意操作。
2、操作过程按对话框(如图5)操作即可。
3、运行结果(1)标定参数结果:a=2.6288,b=0.2361,c=0.0,如图6所示,不过大看show report 里面参数更准确。
(2)K-Factor Flow:如图7所示。
第三步:创建综合阻抗因子f (Rij) (Synthetic Friction Factors)1、数据准备(1)创建空矩阵“Friction Factor shell”;(2)已标定的a、b、c值;(3)阻抗(最短路径)矩阵。
多类重力场模型的精度分析及联合确定GPS点正常高的方法张兴福;李博峰;魏德宏;刘成【摘要】针对模型尺度参数ae对高程异常计算的影响进行数值分析;利用各模型位系数方差信息及区域高精度GPS/水准数据分析国际上新近公布的ITG-GRACE2010S、AIUB-GRACE03S、EIGEN-6C、GOCO02S、DIR_R3、TIM_R3、SPW_R2、gif48以及EGM2008多类重力场模型对应不同谱域的位系数精度;提出采用简单谱组合方法和加权谱组合方法来提高高程异常的计算精度.在试验区域,计算结果表明,各模型的中低阶(约135阶)位系数整体精度要优于EGM2008模型,gif48和EIGEN-6C模型的整体精度均优于同阶次的EGM2008模型,简单谱组合方法和加权谱组合方法均能提高区域模型高程异常精度.【期刊名称】《测绘学报》【年(卷),期】2013(042)001【总页数】7页(P6-12)【关键词】地球重力场模型;高程异常谱分析;谱组合;GPS高程转换;精度分析【作者】张兴福;李博峰;魏德宏;刘成【作者单位】广东工业大学测绘工程系,广东广州510006;同济大学测绘与地理信息学院,上海200092;广东工业大学测绘工程系,广东广州510006;铁道第三勘察设计院集团有限公司测绘分院,天津300251【正文语种】中文【中图分类】P2231 引言高分辨率、高精度的地球重力场模型在利用GPS技术快速确定正常高过程中发挥重要的作用[1-2],随着 CHAMP、GRACE 和 GOCE 等重力卫星的成功实施,全球重力场模型的中低阶位系数的精度提高了约两个量级甚至更高[3-10]。
因此,如何综合利用由不同反演方法及数据源求得的具有不同精度及分辨率的地球重力场模型并分析其用于GPS正常高测量的精度,具有重要的现实意义。
2008年EGM2008模型的公布,使得重力场模型所表示的全球大地水准面的精度和分辨率均达到了前所未有的水平,其分辨率约5′[11-15]。
ICGEM最新重力场模型精度比较分析
侯博文;黄强
【期刊名称】《科技创新与应用》
【年(卷),期】2018(000)013
【摘要】人类有关于地球重力场的研究可以追溯到上个世纪,重力场的研究一直是地球物理、大地测量的核心部分.地球重力场模型就是将全球重力场模型化、简单化,它的优点是可以很方便地计算出有关重力场的各种数据.其中包括高程异常、重力异常、大地水准面差距、垂线偏差等.所以说重力场模型的建立对于重力场理论研究有着极大的推动作用.因为我国采用的是正常高高程系统,所以似大地水准面精化对高程测量就有很高的研究价值,实质上就是确定高程异常值.利用重力场模型可以在很高的精度保证前提下快速确定一个区域的高程异常值.德国地学中心的网站上公布了从1966至今的主流重力场模型,文章主要研究内容就是对目前国际上主流的几个重力场模型进行精度的比较和分析.
【总页数】3页(P10-12)
【作者】侯博文;黄强
【作者单位】中国地震局第二监测中心,陕西西安 710000;成都理工大学地球科学学院,四川成都 610059
【正文语种】中文
【中图分类】P223
【相关文献】
1.重力场模型研究进展及最新重力位模型精度比较分析
2.EGM2008、EGM96、DQM2006三种地球重力场模型的比较分析
3.GRACE RL06与RL05时变重力场模型数据初步比较分析
4.多类地球重力场模型的高程异常精度比较
5.几种卫星测高海洋重力场模型精度比较分析
因版权原因,仅展示原文概要,查看原文内容请购买。