重力模型

2000重力场模型求正常重力正常重力是地球表面上物体受到的重力加速度，通常被定义为9.8 m/s²。

这个数值是根据重力场模型推导出来的，而重力场模型是描述地球上物体受到的重力力场的数学模型。

重力场模型是基于牛顿的万有引力定律建立的。

根据万有引力定律，两个物体之间的引力与它们质量的乘积成正比，与它们之间距离的平方成反比。

而地球上的重力场是由地球的质量分布所引起的。

在重力场模型中，地球被假设为一个完全球对称的物体，其质量均匀分布在球心。

根据这个假设，可以推导出在地球表面上的物体受到的重力加速度与离地球球心距离的平方成反比。

而由于地球的形状是略微扁球形的，所以这个重力加速度在地球不同的地方会略有不同。

重力场模型还考虑了地球自转对重力加速度的影响。

由于地球自转，地球上的物体会受到离心力的作用，此离心力会使重力加速度在赤道附近稍微减小，而在极地附近稍微增大。

这就是为什么赤道上的物体相对于极地上的物体所受到的重力稍微减小的原因。

除了地球的自转，重力场模型还考虑了地球上的地形对重力加速度的影响。

由于地球上存在地形起伏，不同地方的海拔高度不同，这也会对重力加速度产生影响。

一般来说，海拔越高，离地球球心的距离就会增加，因此重力加速度会稍微减小。

同时，地球上的重力场还受到地下物体的影响，例如地下的岩石和水体等，这些物体也会对重力加速度产生微弱的影响。

根据重力场模型，我们可以计算出地球上不同地方的重力加速度。

一般来说，地球表面上的重力加速度大约为9.8 m/s²，但实际上它在不同地方会略有差异。

例如在赤道附近，重力加速度约为9.78 m/s²，而在极地附近则约为9.83 m/s²。

同时，在海拔高度较高的地方，重力加速度也会稍微减小。

正常重力是地球上物体受到的重力加速度，它是根据重力场模型推导出来的。

重力场模型考虑了地球的球形、自转、地形和地下物体对重力加速度的影响，因此地球上的重力加速度在不同地方会略有不同。

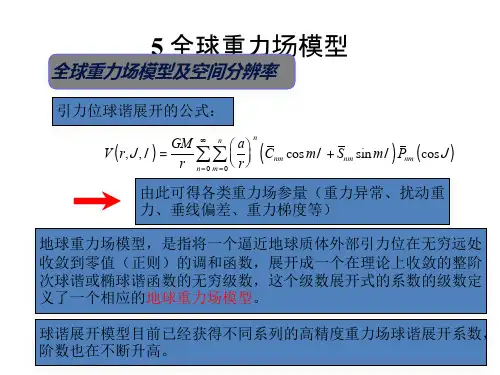
第六章 地球重力场模型随着空间技术的进步和发展，现在不但有可能根据卫星轨道根数的变化精确地确定地球动力形状因子2J ，而且有可能结合卫星测高仪、卫星追踪卫星技术、卫星重力梯度仪等空间技术的测量结果以及地面重力测量结果计算出地球大地位球函数展开的高阶项系数。

以一组数值球函数展开系数表示的地球大地位称为地球重力场模型，地球重力场模型一方面支持卫星轨道的精确计算，另一方面可以给出地面上的长波重力异常场，为研究地球内部结构及其动力学过程提供重要的地面约束条件。

6.1 大地位的球函数展开现将第二章已经讨论过的大地位球函数展开中的有关公式汇总如下。

用r 表示地球外部空间任一点P 的径矢，则根据（2.2.18）式，地球在P 点的大地位球函数展开表示为其中kM 为地球的地心引力常数，a 为地球的赤道半径，θ、λ分别为P 点的地心余纬和经度，(cos )mn P θ为cos θ的n 阶m 次伴随勒让德多项式，(cos )cos mn P m θλ、(cos )sin mn P m θλ为归一化的n 阶m 次球面函数，根据（2.2-1.3）式、（2.2-1.6）式和（2.2-1.8）式，()n P x 、()n P x 、()mn P x 、()mn P x 分别为m n c 、m n s 和mn c 、mn s 分别为大地位球函数展开系数和规一化的大地位球函数展开系数，根据（2.2.20）式，有根据（2.3.4）式、（2.3.5）式，大地位二阶球函数展开系数等于其中A 、B 、C 分别为地球绕1Ox 、2Ox 和其旋转轴3Ox 轴的转动惯量，12I 、23I 、13I 分别为地球绕相应轴的惯性积，大地位球函数展开有时写成下面的形式nm J 、nm K 与大地位球函数展开系数m n c 、m n s 之间的关系为2J 称为地球的动力形状因子。

当3n 时，()n P x 、()mn P x 的表达式如表6.1.1所示。

重力模型公式重力模型公式，这可是物理学中的一个重要概念呢！咱先来说说啥是重力模型公式。

简单来讲，它就是用来描述两个物体之间引力大小的数学表达式。

就像地球吸引着我们，月亮围绕着地球转，这些现象背后都离不开重力模型公式的作用。

那重力模型公式到底长啥样呢？它是 F = G×(m1×m2) / r²。

这里的F 表示两个物体之间的引力，G 呢是引力常量，m1 和 m2 分别是两个物体的质量，r 是两个物体质心之间的距离。

我还记得有一次，我带着一群小朋友去科技馆玩。

走到一个关于重力的展示区，有个小朋友特别好奇地问我：“老师，为什么苹果会从树上掉下来呀？”我就笑着告诉他：“这就是重力在起作用呀，咱们可以用重力模型公式来计算苹果受到的地球引力有多大呢。

”然后我就给他简单讲了讲这个公式。

这公式在生活中的应用可多啦！比如说，咱们发射卫星的时候，就得好好算算卫星和地球之间的引力，保证卫星能在预定的轨道上运行。

要是算错了，那卫星可就不知道跑到哪里去咯！在天文学里，科学家们也是靠着这个公式去研究天体之间的相互作用。

比如说，通过观测行星的运动轨迹，再结合重力模型公式，就能推测出那些我们看不到的天体的质量和位置。

回到咱们的日常生活，你想想，为什么我们跳起来最后还是会落到地上？这就是因为地球对我们的引力。

要是没有这个引力，那可就好玩啦，咱们说不定就飘在空中，像气球一样到处乱飞！再比如，建筑工人在盖高楼的时候，也得考虑重力的影响。

如果不考虑清楚，房子可能就不稳，说不定哪天就歪了倒了。

还有啊，当我们扔东西的时候，东西飞行的轨迹也和重力有关。

扔出去的球会先往上飞一段，然后在重力的作用下开始下落。

总之，重力模型公式虽然看起来有点复杂，但它真的无处不在，影响着我们生活的方方面面。

通过对重力模型公式的学习和了解，我们能更好地理解这个世界的运行规律。

它就像是一把神奇的钥匙，能帮助我们打开探索宇宙奥秘的大门。

所以啊，同学们，可别小看这个公式，它里面蕴含着无穷的智慧和力量，等着我们去发现和运用！。

重力模型的约束条件公示
重力模型基于牛顿的重力法则，它指出出行分布与小区的产生量、吸引量和小区之间的交通方便程度等因素相关。

它基本的假设是：交通小区i与j间的出行分布量与小区i的出行发生量、小区j的出行吸引量成正比，与小区i和j之间的交通阻抗成反比。

综合考虑了影响出行分布的区域社会经济增长因素和出行空间、时间阻碍等因素，是国内交通规划中使用最广泛的方法。

双约束重力模型满足交通小区交通产生量与吸引量与小区交通
总量之间约束条件，交通阻抗函数是交通小区之间出行阻抗的函数，用于拟合出行分布与出行代价的关系，体现了小区间的交通阻力，出行代价通常用时间、费用、综合性的广义费用作为参数测度。

实践证明交通阻抗函数的综合性越强，所包含的因素越多模型越精确，但交通阻抗函数的复杂度与模型的收敛性是一对反比关系。

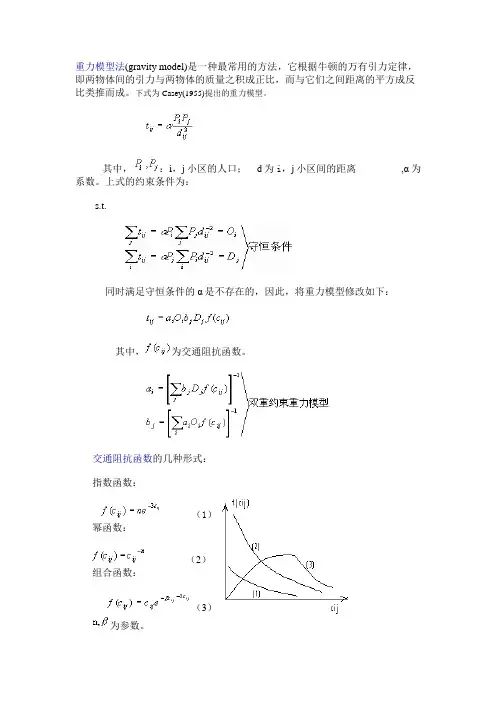
重力模型法(gravity model)是一种最常用的方法，它根据牛顿的万有引力定律，即两物体间的引力与两物体的质量之积成正比，而与它们之间距离的平方成反比类推而成。

下式为Casey(1955)提出的重力模型。

其中，：i，j小区的人口； d为i，j小区间的距离,α为系数。

上式的约束条件为：s.t.同时满足守恒条件的α是不存在的，因此，将重力模型修改如下：其中，为交通阻抗函数。

交通阻抗函数的几种形式：指数函数：（1）幂函数：（2）组合函数：（3）为参数。

单约束型B.P.R.模型其中，调整系数。

发生侧得到保证，即：以下以幂指数交通阻抗函数为例介绍其计算方法：第1步令m=0，m为计算次数。

第2步给出n（可以用最小二乘法求出）。

第3步令第4步求出第5步收敛判定。

若下式满足，则结束计算；反之，令m+1=m，返回第２步重复计算。

,作业：按上次作业给出的现状OD表和将来生成、发生与吸引交通量，利用下式重力模型和弗拉塔算法，求出将来OD表。

收敛标准。

重力模型:其中，，，。

读者也可以利用以前给出的现状分布交通量和表4-1示现状行驶时间，估计出这3个参数。

表4-1 现状行驶时间表4-2将来行驶时间解：利用重力模型求解分布交通量如下：同理，可以计算出其它各交通小区之间的交通量如下表所示。

重力模型的优点：a.直观上容易理解；b.能考虑路网的变化和土地利用对人们的出行产生的影响；c.特定交通小区之间的OD交通量为零时，也能预测；d.能比较敏感地反映交通小区之间行驶时间变化的情况。

重力模型的缺点：a.重力模型仅仅是将物理法则简单直观上容易理解；b.能考虑路网的变化和土地利用对地应用到社会现象，尽管有类似性，需要更加贴合人们出行的方法；c.一般，人们的出行距离分布在全区域并非为定值，而重力模型将其视为定值；d.交通小区之间的行驶时间因交通方式和时间段的不同而异，而重力模型使用了同一时间；e.求内内交通量时的行驶时间难以给出；f.交通小区之间的距离小时，有夸大预测的可能性；g.利用重力模型计算出的分布交通量必须借助于其它方法进行收敛计算。

重力模型的过程和原理教案重力模型是一种经济地理学中常用的分析工具，用于研究地理空间内不同地区之间的贸易、人口流动、投资等现象。

它通过考虑地理距离和经济规模大小两个因素，揭示了地理空间的相互作用对区域之间的联系和互动产生的影响。

一、重力模型的基本原理重力模型的基本原理是基于物理学中的引力定律，即两个物体之间的引力与它们的质量成正比，与它们之间的距离成反比。

将这个物理定律应用到经济地理学中，我们可以认为两个地区之间的联系程度与它们的经济规模大小成正比，与它们之间的地理距离成反比。

重力模型的基本公式可以表示为：T = k * (M1 * M2) / D^a，其中T表示两个地区之间的贸易、人口流动或投资的强度，k是一个常数，M1和M2分别表示两个地区的经济规模，D表示两个地区之间的地理距离，a是一个指数，用于衡量地理距离对联系程度的影响。

二、重力模型的应用过程1. 数据收集：首先需要收集关于地区经济规模、地理距离以及贸易、人口流动或投资强度的数据。

这些数据可以来自于统计局、商业机构、调查问卷等渠道。

2. 变量定义：根据研究的具体对象和目的，将收集到的数据转化为模型中的变量。

一般来说，经济规模可以用GDP、人口数量或其他相关指标表示，地理距离可以用实际距离或交通时间等方式衡量，贸易、人口流动或投资强度可以用贸易额、人口流动量或投资金额等指标表示。

3. 模型估计：根据收集到的数据和变量定义，利用计量经济学中的方法对重力模型进行估计。

传统的估计方法包括普通最小二乘法（OLS）、仪器变量法（IV）等。

4. 参数解释和检验：根据估计结果，解释模型中的参数。

一般来说，经济规模的系数表示经济规模对联系程度的影响，指数a的值表示地理距离对联系程度的影响。

为了确保参数的统计显著性，还需要进行假设检验。

5. 模型拟合度检验：为了评估模型的拟合程度和预测能力，一般需要计算模型的拟合度指标，比如决定系数（R-squared）等。

重力模型的过程和原理
重力模型指的是一种模拟地球引力和物体运动的模型。

具体的过程和原理如下：
1.建立地球引力场模型：根据地球的质量、半径和万有引力定律，可以建立一个描述地球引力场的数学模型。

2.设定初始条件：包括物体的初始位置、初始速度、引力场的初始状态等。

3.计算物体在引力场中受力：根据万有引力定律，计算物体受到的引力大小和方向。

4.计算物体运动轨迹：根据牛顿第二定律，将物体所受的引力转化为物体的加速度，并计算物体在引力场中的运动轨迹。

5.不断迭代计算：为了得到更准确的运动轨迹，需要不断迭代计算，直到达到预设的停止条件。

重力模型的原理是基于万有引力定律和牛顿第二定律的基础物理学原理，通过计算物体在引力场中的运动轨迹，模拟地球引力和物体运动的过程。

它可以用于研究天体运动、天文现象、航天等领域的问题，也可以用于游戏和动画制作中。

重力模型法(gravity model)是一种最常用的方法，它根据牛顿的万有引力定律, 即两物体间的引力与两物体的质量之积成正比，而与它们之间距离的平方成反 比类推而成。

下式为Casey(1955)提岀的重力模型。

其中，‘ ''：i ，j 小区的人口；d 为i ,j 小区间的距离，a系数。

上式的约束条件为：同时满足守恒条件的a 是不存在的，因此，将重力模型修改如下:知=內如问他)交通阻抗函数的几种形式: 指数函数:幕函数：/(唧F组合函数：「为参数。

守叵条件(3)j 单约束型B.P.R.模型其中，'“调整系数。

j发生侧得到保证，即：%）讨_1以下以幕指数交通阻抗函数为例介绍其计算方法: 第1步令m=0，m为计算次数第2步给出n （可以用最小二乘法求出）。

＜=1,求出丐）第3步令—1第4步求出第5步收敛判定。

若下式满足，则结束计算；反之，令m+1=m，返回第2步重复计算。

1 - X 好仏严＜ 1 +启 1 - * 琦处：讥＜ 1 +療作业：按上次作业给出的现状0D表和将来生成、发生与吸引交通量，利用下式重力模型和弗拉塔算法，求出将来0D表。

收敛标准—1，:''重力模型：其中，八…汀，「‘亠，「。

读者也可以利用以前给出的现状分布交通量和表4-1示现状行驶时间，估计出这3个参数。

解：利用重力模型求解分布交通量如下：- 0.183x(38.2x38.51^/4.0^ -96.4切=0.183x (；38L2 x M.3)1153 /= 74.56 -0.183X(38.2X37.9)2/il.01J3S = 20J同理，可以计算出其它各交通小区之间的交通量如下表所示a. 直观上容易理解；b. 能考虑路网的变化和土地利用对人们的出行产生的影响;c. 特定交通小区之间的OD 交通量为零时，也能预测；d. 能比较敏感地反映交通小区之间行驶时间变化的情况。

重力模型的缺点：a. 重力模型仅仅是将物理法则简单直观上容易理解；b. 能考虑路网的变化和土地利用对地应用到社会现象，尽管有类似性，需要更 加贴合人们出行的方法；c. 一般，人们的出行距离分布在全区域并非为定值，而重力模型将其视为定 值；d. 交通小区之间的行驶时间因交通方式和时间段的不同而异，而重力模型使用 了同一时间；e 求内内交通量时的行驶时间难以给出；f. 交通小区之间的距离小时，有夸大预测的可能性；g. 利用重力模型计算出的分布交通量必须借助于其它方法进行收敛计算。