螺线管自感系数的讨论

2019年军队文职人员招聘考试理工学类-数学2+物理试卷（解析）1考察极限的定义。

在(-1,0]内，，而在(0,1)内，即左极限不等于右极限。

所以极限不存在。

故正确答案为D。

2考察复合函数求导。

方程两边求导可得，将代入可得：，计算两边取e的指数，得：由此可得到。

故正确答案为C。

3考察定积分的计算。

因为在[0,1)的积分大于0，在[1,2]的积分小于等于0。

所以有绝对值符号之后，应全为正。

所以。

故正确答案为B。

4考察变限积分求导。

由题意，交换积分上下限后为，则，当时，。

故正确答案为B。

5考察矩阵的性质。

只有在AB=BA的情况下，满足A项和B项才成立。

对A项，若AB=BA，矩阵的乘法交换才满足：B项的计算过程为：等式右边，当AB=BA时C项一定不对，例如单位矩阵E有，，，故C项不对。

D项为可逆矩阵的性质，正确，选D项。

故正确答案为D。

6考察矩阵的运算。

数域上矩阵与矩阵的乘积指的是这样一样的一个矩阵，这个矩阵的第行第列的元素等于的第行的元素与B的第列的对应元素的乘积之和：根据上述乘法运算定义，将初等矩阵左乘矩阵得：可知是将2、3两行的交换。

故正确答案为A。

7考察行列式计算。

计算行列式时，可以用行展开和列展开的方式。

行列式等于它任意一行（列）的所有元素与它们对应代数余子式的乘积的和，对行列式的第三行展开可得：，解得。

故正确答案为B。

8考察矩阵的特征值。

矩阵特征值与其逆矩阵的特征值的关系是：的特征值为的特征值倒数。

非奇异矩阵存在可逆矩阵。

由于的一个特征值为2，又逆矩阵的特征值为对应矩阵的倒数，所以因此为。

故正确答案为C。

9考察参数方程与直角坐标系之间的关系。

参数方程的x，y对应坐标上的横纵坐标，求解时需要把握它们的对应关系。

将带入，解得或者。

将上述结果带入得到，即是曲线在处的法线与交点的纵坐标。

故正确答案为A。

10考察定义在平面上的函数，求趋于一点的极限。

观察题目可知，当的时候，有。

那么原极限为（分子分母最高次数为四次）。

无限长螺线管内部的磁感应强度是一个涉及电磁学和磁场理论的复杂问题。

螺线管是一种导体绕成的螺旋线，当电流通过螺线管时会产生磁场。

在这种情况下，我们需要计算螺线管内部的磁感应强度，以了解其在各种应用中的行为。

1. 螺线管磁场的产生我们需要了解螺线管内部磁感应强度的产生机制。

当电流通过螺线管时，会形成环绕螺线管的磁场，这是由安培定律和毕奥-萨伐尔定律所描述的。

根据这两个定律，我们可以得知螺线管内部的磁场与电流强度、螺线管的几何形状和材料特性有关。

2. 长螺线管近似模型在实际应用中，无限长螺线管往往是一个理想化模型，简化了计算。

通过这种近似模型，我们可以用简单的数学方法来描述螺线管内部的磁感应强度。

通过对螺线管的几何形状和电流分布进行合理的假设，我们可以得到关于磁场分布的定量描述。

3. 磁感应强度的计算针对螺线管内部磁感应强度的计算，可以利用比奥萨伊特定律和安培环路定律。

根据比奥萨伊特定律，我们可以得到磁场的分布规律，而根据安培环路定律，可以得到螺线管内部的磁感应强度。

在具体计算时，需要考虑到螺线管的半径、线圈的匝数、电流的大小等因素，进行定积分的计算，从而得到磁感应强度的具体数值。

4. 应用和拓展螺线管是电磁学中常用的元件，它在电磁学实验、电磁感应、电子技术等领域都有着重要的应用。

对于螺线管内部磁感应强度的研究，不仅可以帮助我们深入理解电磁学原理，还可以指导工程实践中的设计和应用。

对于其他形状的线圈和螺线管，我们也可以借鉴类似的方法，拓展研究范围，探讨不同形状线圈的磁场特性和应用。

螺线管内部的磁感应强度是一个具有理论和实际意义的问题。

通过深入研究和计算，我们可以揭示螺线管磁场的分布规律，指导相关应用，并对电磁学理论的深化和拓展提供有益的参考。

当然，在实际工程应用中，还需要考虑到其他因素的影响，进行综合分析和研究。

希望有关领域的学者和工程师可以进一步探索这一问题，为电磁学和应用技术的发展贡献自己的力量。

环形螺线管的磁感应强度一、什么是环形螺线管？环形螺线管，又称为环形线圈，是一种由导线绕成的环状结构。

它在电磁学中有着重要的应用，可以产生强大的磁场。

环形螺线管通常由绝缘导线绕成多圈，形成一个密封的环形结构。

二、环形螺线管的磁感应强度的基本概念环形螺线管的磁感应强度是指在螺线管内部的磁场强度大小。

磁感应强度是描述磁场强弱的物理量，也可以称为磁场密度。

其单位是特斯拉（T）。

三、环形螺线管磁感应强度的计算方法要计算环形螺线管的磁感应强度，可以使用安培定理和比奥—萨伐尔定律。

根据安培定理，通过螺线管的电流将产生一个沿着螺线管轴向的磁场。

而根据比奥—萨伐尔定律，可以推导出螺线管中心轴上的磁感应强度公式：B=μ0⋅n⋅I 2⋅R其中，B代表磁感应强度，μ0代表真空中的磁导率（4π×10−7T m/A），n代表螺线管匝数，I代表通过螺线管的电流，R代表螺线管的半径。

四、影响环形螺线管磁感应强度的因素1.磁感应强度与电流的关系：由磁感应强度公式可知，磁感应强度与电流成正比关系，即电流越大，磁感应强度越大。

2.磁感应强度与匝数的关系：磁感应强度与螺线管匝数成正比关系，匝数越多，磁感应强度越大。

3.磁感应强度与螺线管半径的关系：磁感应强度与螺线管半径成反比关系，半径越大，磁感应强度越小。

五、环形螺线管在实际应用中的例子1.电感器件：环形螺线管常用作电感器件，可以用于电子电路中的滤波、调节电压和变换电流等作用。

2.电磁铁：环形螺线管通过通电产生的强磁场可以使其具备吸附物体的能力，常用于电磁吸盘、电磁闸等设备中。

3.磁共振成像（MRI）：医学中常用的磁共振成像仪就是利用了环形螺线管产生的强磁场对人体进行成像。

4.粒子加速器：环形螺线管作为加速器的主要组成部分之一，可以通过调节电流产生强磁场，加速带电粒子。

六、环形螺线管在工程设计中的优化在设计环形螺线管时，需要综合考虑多个因素，以优化磁感应强度的输出。

1.合理选择导线材料：导线材料的电导率会影响电流通过螺线管的效率，选择高电导率的材料可以减少能量损耗。

磁场的能量公式
1. 自感线圈磁场能量公式。

- 对于一个自感系数为L的线圈，当通过的电流为I时，其储存的磁场能量W = (1)/(2)LI^2。

- 推导过程：当电路中的电流I发生变化时，自感电动势E = - L(di)/(dt)。

在建立电流I的过程中，电源克服自感电动势做功，这个功就转化为磁场的能量。

根据能量守恒定律，设电流从0增加到I，电源克服自感电动势做的功W=∫_0^tEidt=∫_0^ILi
di=(1)/(2)LI^2。

2. 磁场能量密度公式。

- 在均匀磁场中，磁场能量密度w=(1)/(2)frac{B^2}{μ}，其中B是磁感应强度，μ是磁导率（对于真空μ=μ_0，对于介质μ = μ_rμ_0，μ_r是相对磁导率）。

- 推导过程：对于长直螺线管，内部磁场B=μ nI（n是单位长度的匝数），自感系数L=μ n^2V（V是螺线管的体积）。

根据W=(1)/(2)LI^2，将L和I=(B)/(μ n)代入可得W=(1)/(2)frac{B^2}{μ}V，所以磁场能量密度w = (W)/(V)=(1)/(2)frac{B^2}{μ}。

对于非均匀磁场，可以通过对体积元dV积分W=∫_Vw dV=∫_V(1)/(2)frac{B^2}{μ}dV
来计算磁场的总能量。

高中物理演示自感现象教案
实验名称：自感现象
实验目的：通过观察自感现象，掌握自感现象的实验方法和规律。

实验器材：螺线管、电源、指南针、导线、开关、玻璃板等。

实验原理：自感现象是一个螺线管中通过电流时，螺线管内部会产生磁感应强度从而引起螺线管自身发生的感应电流的现象。

实验步骤：
1. 将螺线管放置在桌面上，并连接螺线管的两端以及指南针与电源、开关和导线。

2. 将指南针靠近螺线管，观察指南针指向的方向。

3. 打开电源，通过导线使电流通过螺线管。

4. 观察指南针指向的变化。

实验结果：
1. 当电流通过螺线管时，螺线管内部产生的磁场会引起指南针的指向发生变化。

2. 当电流方向改变时，指南针的指向也会发生变化。

实验结论：自感现象就是螺线管中通过电流时，产生的磁场引起螺线管自身感应电流的现象。

当电流方向改变时，感应电流方向也发生改变。

拓展实验：
1. 将玻璃板放置在螺线管底部，观察自感现象发生的变化。

2. 研究不同电流强度对自感现象的影响。

思考问题：
1. 什么是自感现象？它与电感有何区别？
2. 为什么在螺线管中通过电流时会产生自感现象？
师生讨论：
1. 请同学们分享自己观察到的自感现象，并讨论其中的规律性。

2. 老师与学生一起探讨自感现象在生活中的应用，如电磁感应等。

实验总结：
通过本次实验，学生们深刻了解了自感现象的实验方法和规律，并且认识到了自感现象在电磁学中的重要性。

希望同学们能够在以后的学习中继续深入探索电磁学知识，不断提高自己的实验技能和物理素质。

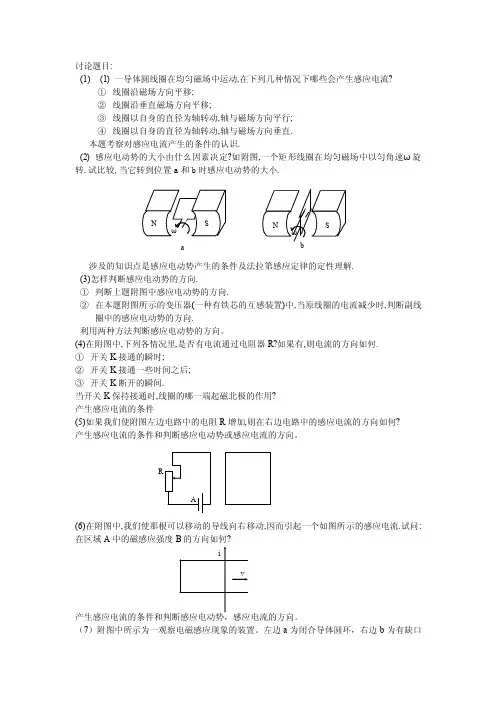
讨论题目:(1) (1) 一导体圆线圈在均匀磁场中运动,在下列几种情况下哪些会产生感应电流?① 线圈沿磁场方向平移;② 线圈沿垂直磁场方向平移;③ 线圈以自身的直径为轴转动,轴与磁场方向平行; ④ 线圈以自身的直径为轴转动,轴与磁场方向垂直. 本题考察对感应电流产生的条件的认识.(2) 感应电动势的大小由什么因素决定?如附图,一个矩形线圈在均匀磁场中以匀角速ω旋转.试比较,当它转到位置a 和b 时感应电动势的大小.涉及的知识点是感应电动势产生的条件及法拉第感应定律的定性理解.(3)怎样判断感应电动势的方向.① 判断上题附图中感应电动势的方向.② 在本题附图所示的变压器(一种有铁芯的互感装置)中,当原线圈的电流减少时,判断副线圈中的感应电动势的方向.利用两种方法判断感应电动势的方向。

(4)在附图中,下列各情况里,是否有电流通过电阻器R?如果有,则电流的方向如何. ① 开关K 接通的瞬时; ② 开关K 接通一些时间之后;③ 开关K 断开的瞬间.当开关K 保持接通时,线圈的哪一端起磁北极的作用?产生感应电流的条件(5)如果我们使附图左边电路中的电阻R 增加,则在右边电路中的感应电流的方向如何? 产生感应电流的条件和判断感应电动势或感应电流的方向。

(6)在附图中,我们使那根可以移动的导线向右移动,因而引起一个如图所示的感应电流.试问:在区域A 中的磁感应强度B 的方向如何?（7）附图中所示为一观察电磁感应现象的装置。

左边a 为闭合导体圆环，右边b 为有缺口a的导体圆环，两环用细杆连接支在O 点，可绕O 在水平面内自由转动。

用足够强的磁铁的任何一极插入圆环。

当插入环a 时，可观察到环向后退；插入环b 时，环不动，试解释所观察到的现象。

当用S 极插入环a 时，环中的感应电流方向如何？ 产生感应电流的条件和判断感应电动势或感应电流的方向。

（8）在下列各种情况下，闭合线圈在均匀磁场中转动，是否回产生感应电流？并指出其方向。

第8章变化的电磁场一、选择题1.若用条形磁铁竖直插入木质圆坏，则在坏中是否产生感应电流和感应电动势的判断](A)产生感应电动势，也产生感应电流(B)产生感应电动势，不产生感应电流(C)不产生感应电动势，也不产生感应电流(D)不产生感应电动势,产生感应电流T 8-1-1 图2.关于电磁感应，下列说法中正确的是[](A)变化着的电场所产生的磁场一定随吋间而变化(B)变化着的磁场所产生的电场一定随时间而变化(C)有电流就有磁场，没有电流就一定没有磁场(D)变化着的电场所产牛:的磁场不一定随时间而变化3.在有磁场变化着的空间内，如果没有导体存在，则该空间[](A)既无感应电场又无感应电流(B)既无感应电场又无感应电动势(C)有感应电场和感应电动势(D)有感应电场无感应电动势4.在有磁场变化着的空间里没有实体物质，则此空间屮没有[](A)电场(B)电力(C)感生电动势(D)感生电流5.两根相同的磁铁分别用相同的速度同时插进两个尺寸完全相同的木环和铜环内，在同一时刻，通过两环包闱面积的磁通量[](A)相同(B)不相同，铜环的磁通量大于木环的磁通量(C)不相同，木环的磁通量大于铜环的磁通量(D)因为木环内无磁通量，不好进行比佼_6.半径为G的圆线圈置于磁感应强度为一B的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为几当把线圈转动使其法向与〃的夹角曰=6(?时，线圈中通过的电量与线圈面积及转动的时间的关系是](A)与线圈面积成反比，与时间无关(B)与线圈面积成反比，与时间成正比(C)与线圈面积成正比，与时间无关(D)与线圈面积成正比，与时间成正比7.一个半径为r的圆线圈置于均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R・当线圈转过30。

时，以下各量中，与线圈转动快慢无关的量是[](A)线圈中的感应电动势(B)线圈中的感应电流(C)通过线圈的感应电量(D)线圈回路上的感应电场& 一闭合圆形线圈放在均匀磁场中，线圈平面的法线与磁场成30。

螺线管自感系数公式
螺线管自感系数公式是描述螺线管自感现象的数学公式，也是电
磁学中比较重要的一部分，本文将对螺线管自感系数公式进行详细的
介绍和解析。

螺线管自感系数公式是一个简单的公式，它由一些基本物理量组成。

这个公式描述了螺线管绕制的线圈中，当电流通过时所产生的磁
场如何影响自身。

螺线管自感是电磁学基础理论中的重要概念，它是
指当螺线产生一个带有电流的磁场时，这个磁场会在螺线内形成一个
感应电动势，即自感电势，同时自感电势与电流成反比。

具体地说，螺线管自感系数公式为：
L = μN²A / l
其中，L表示螺线管的自感系数，单位为亨（H），μ表示磁导率，单位为牛顿/安培的平方，N表示线圈中的匝数，A表示线圈的面积，
单位为平方米，l表示线圈的长度，单位为米。

从公式可以看出，当螺线管中的线圈匝数增加时，自感电势的数
值也会增加；当线圈面积增大时，自感电势也会增大；而当线圈长度
增加时，自感电势则会减小。

螺线管自感系数公式对于磁感应强度和电磁感应现象的研究具有
重要意义。

在工程技术和实际应用中，这个公式被广泛地应用于电化学、电动机和变压器等领域。

总的来说，了解螺线管自感系数公式的原理和应用，不仅有助于我们更好地理解电磁现象和电磁学的基本概念，同时也有助于我们在实际应用中更好地设计和控制电子设备和电机。

关于螺线管内部轴线磁场的探讨B作者：朱昱昌摘要：本文不仅揭示了螺线管内轴线磁场表达式B=（µ0nI/2）（cosβ2-cos β1）能够导出类似于“整体小于部分”的逻辑错误，而且还证明了其收敛结论不能成立。

关键词：螺线管轴线磁场磁场表达式全磁通原理收敛与发散我们从各种版本的《电磁学》中发现：根据毕奥、萨法尔定律直接推导的螺线管内轴线磁场表达式B=（µ0nI/2）（cosβ2-cosβ1）[1. 2]、[2. 1]、[3. 3]、[4. 2]，不仅在具体应用时存在致命的矛盾，而且其关于螺线管内轴线磁场收敛的结论也不能成立。

现详述如下，愿与大家共同分析、探讨，并望大家不吝赐教。

1、螺线管内轴线磁场表达式B=（µ0nI/2）（cosβ2-cosβ1）存在的矛盾1.1、表达式B=（µ0nI/2）（cosβ2-cosβ1）没有保持B与R的反比关系。

因为，载流密绕螺线管是相应单个载流圆形线圈的扩展，是相应单个载流圆形线圈的串联结构。

二者存在必然联系，特别应该保持B与R的反比关系。

例如：把一根载流导线按右手定则沿直圆柱表面回绕一周就构成了一个闭合回路，叫做一个单元线圈（或单个线圈）。

如果把一根载流导线按右手定则沿直圆柱表面紧密回绕N周就构成了一个直螺线管。

显然，这个直螺线管就等于由N个相同的单元线圈按右手定则紧密串联而成。

但是，相应载流单元线圈端面圆心O 处B0=µ0I/2R≠（µ0nI/2）（cosβ2-cosβ1）（注：当n=1时）。

即表达式B=（µ0nI/2）（cosβ2-cosβ1）不能反应多个相同单元线圈串联效果与其中一个单元线圈之间的必然联系，没有保持B与R的反比关系。

1.2、表达式B=（µ0nI/2）（cosβ2-cosβ1）的量纲存在错误。

因为µ0的量纲是：[µ0]＝LMT-2I-2 [3.2]；磁感应强度B的单位是T＝N/A·m ，B的量纲是：[B]＝[N/A·m] =( LMT-2) (I-1L-1)= MT-2I-1 [1. 2]；µ0nI/2的量纲是：[µ0nI/2]＝[µ0] I＝LMT-2I-1。

长直螺线管的自感系数
长直螺线管的自感系数是描述抗干扰特性的一个重要参数，用来表示双端加电后，允许电流在一个特定时间变化以释放电磁能量等测量值。

它对多个开发领域都具有重要意义。

首先，长直螺线管的自感系数具有较强的耐受性，能够抵抗外部辐射的影响，使电流较为稳定。

其次，它能更好地抑制电流波动，降低电流在一定时间内变化的厉害程度；此外，它还具有较高的电容率，可以抑制电流的变化幅度，从而使长直螺线管的电流保持更为稳定和统一，为某些制造工艺提供更好的抗干扰性能。

此外，自感系数也决定了各种类型螺线管在机械性能上的区别。

高自感系数的螺线管能够抑制电流短路引起的损伤；而低自感系数的螺线管则会减少螺线管对整个电路系统的影响。

同时，长直螺线管的自感系数又决定了磁场及其抗力的强弱，从而实现良好的效果。

另外，自感系数可以用作螺线管性能评价的有效指标，从而可以综合考虑各种参数，使其最大值可以达到最优的效果。

此外，长直螺线管的自感系数还对现代物联网产生了深刻的影响。

物联网节点的可靠性在一定程度上也取决于螺线管的自感系数。

由于高自感系数的螺线管能够阻止电流过载以抑制物联网节点的损伤，所以为物联网提供了可靠性保障。

总的来说，自感系数对于长直螺线管来说是一个重要参数，它决定了螺线管的发挥效果，同时也决定了其对多个领域，特别是物联网的发挥效果。

因此，正确估算长直螺线管的自感系数以及准确选择其规格是确保长直螺线管在各领域得到正常运行的重要保障。

螺绕环自感系数公式自感系数（Self-inductance）是电磁学中的一个基本参数，它表示电感器中磁通改变时产生的电感作用。

它可以描述电线圈、螺旋绕线和其他电磁元件的磁特性，为电子设备的设计和分析提供参考。

螺绕环的自感系数是电感器的重要参数，也是设计螺绕线电感器的重要依据。

螺绕环的自感系数可以通过螺绕环自感系数公式来计算。

螺绕环自感系数公式是：L = μ·N²·A/l，其中L是螺绕环的自感系数，μ是空气介质的磁导率，N是螺绕线的匝数，A是螺绕线的截面积，l是螺绕线的总长度。

这个公式不仅可以用来计算螺绕环的自感系数，也可以用来计算螺绕线电感器的磁特性。

首先，我们可以根据公式计算螺绕环的自感系数。

例如，如果螺绕线的参数为μ = 4π×10-7H/m、N = 100、A = 10 mm2、l = 1 m，那么螺绕环的自感系数为L = 4π×10-7H/m×100²×10mm2/1 m = 0.4H。

其次，我们可以根据螺绕环的自感系数来计算电感器的磁特性。

例如，如果我们想知道一个电感器的磁通改变时的感应电压，那么我们可以用螺绕环的自感系数来计算。

具体来说，当磁通改变时，感应电压为：U = - L × di/dt，其中L是螺绕环的自感系数，di/dt表示磁通的变化率。

因此，螺绕环的自感系数是电感器的重要参数，它可以用来计算螺绕环的自感系数，也可以用来计算电感器的磁特性。

螺绕环自感系数公式是电感器设计的基础，也是电子设备分析的依据。

螺绕环自感系数公式是一个非常有用的工具，它可以帮助我们更好地理解电感器的工作原理，也可以帮助我们更好地设计电子设备。

无限长均匀载流圆柱形导线内部自感系数计算
曾晓英
【期刊名称】《重庆交通大学学报（自然科学版）》
【年(卷),期】2002(021)002
【摘要】从"磁通链"的定义出发,讨论了5种计算无限长均匀载流圆柱形导线内部单位长度自感系数的方法,并将其结果进行了比较.
【总页数】2页(P126-127)
【作者】曾晓英
【作者单位】长沙交通学院信息与计算科学系,湖南长沙410076
【正文语种】中文
【中图分类】O441
【相关文献】
1.无限长均匀载流圆柱面内部磁感应强度的计算方法总结 [J], 魏茂梅
2.无限长载流直导线旁电子运动轨迹探寻 [J], 潘庆
3.有限长密绕圆柱形螺线管自感系数的精确计算 [J], 江俊勤
4.FlexPDE模拟四条平行载流无限长直导线周围磁场 [J], 刘小利;袁晓燕
5.用镜像法通过矢势计算无限长载流直导线的磁场强度 [J], 周炳卿
因版权原因，仅展示原文概要，查看原文内容请购买。

實驗四 螺線管的自感【目的】藉測量LC 電路(如圖)的自然振盪頻率，以推算螺線管的自感。

【儀器】Fig. 4-1螺線管自感實驗儀器及裝置(1)示波器…..............1台 (7)電差頭………………….2個 (2)函數產生器…..........1台 (8)螺線管1組…………….7個 (3)電子數位式計數器………1台 (9)1200圈線圈…………....1個 (4) BNC 接頭………........1個 (10)游標尺………………...1支 (5)470pF 及1nF 電容器各一個 (11)捲尺…………………...1個 (6)接線盒…………………1個 (12)接線…………………...1組【原理】由於外界磁通密度的變化，可感應引起LC 電路(如圖)發生自發性的電流接盪，其自然震盪頻率f 0可由示波器讀出，而自然震盪角頻率ω0和電路中線圈的自感值L 以及總電容C t 值有下列關係(參考資料1，2)tLC f 1200== 　ωπ （１）C t 為外電路所接之電容C 值以及示波器內部的輸入電容C i (C i 值大小標明在示波器的輸入端)的總和(由圖9-2可見此兩電容並聯)，故總電容值應為兩者的和)。

由(1)是可推得線圈的自感值tC f L 20241π= （２）i t C C C += （3）但是由於示波器的內電阻R i 在震盪迴路中會造成阻尼震盪，因此將使得共振頻率產生約1%的微小誤差。

理論上，當螺線管無限長時(也就是螺線管的長度L 遠大於其半徑r 值)，其自感為(參考資料1，3)lr N L 220πμ= （4）N 為螺線管所有線圈的圈數。

事實上，式( 4 )僅能用於L >> r 的情況，當線圈＜１０＜lr時，下列的進似計算自感值可得較高的準確性：(參考資料4)4326l r r N 102.1L ⎪⎭⎫ ⎝⎛⨯=- （5）r 47λΝ102.1L 4326 log log log +⎪⎪⎭⎫ ⎝⎛⨯=- (6) 【注意事項】不要讓一個強亮光點在示波器螢幕上停留太久，以免螢幕受損。