2006典型例题解析--第2章-静定结构内力计算
- 格式:docx
- 大小:1.76 MB
- 文档页数:25

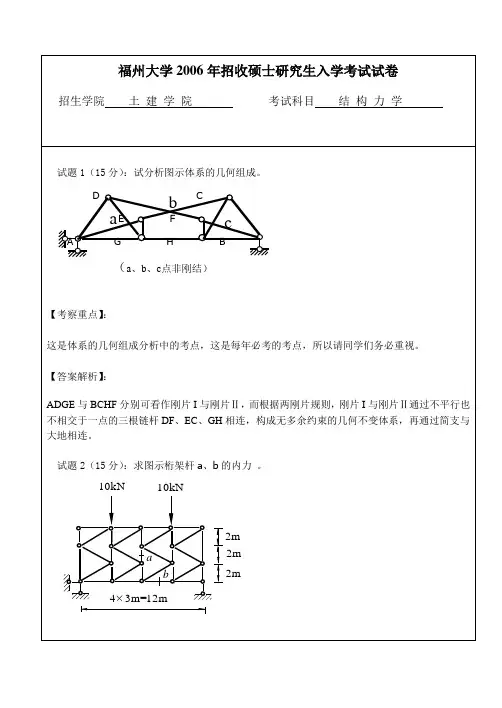

结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
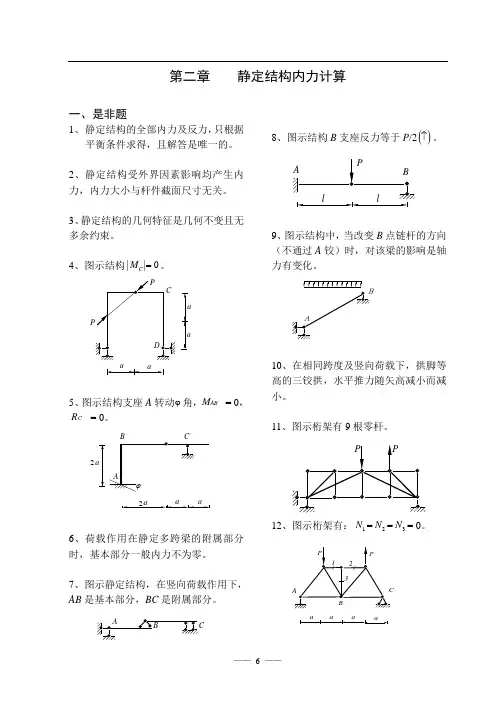
1-1(a)(解原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (c)[(c-1)(a)(a-1)(b)(b-1)*(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)!(d-1) (d-2) (d-3)解 原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e)~解 原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)[解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相(d )(e )(e-1)AB}AB (e-2)(f )(f-1)连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
第二章 静定结构内力计算一、是非题1、 静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图示结构||M C =0。
aa5、图示结构支座A 转动ϕ角,M AB = 0, R C = 0。
BCaaAϕ2a26、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图示静定结构,在竖向荷载作用下, AB 是基本部分,BC 是附属部分。
ABC8、图示结构B 支座反力等于P /2()↑。
9、图示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图示桁架有9根零杆。
12、图示桁架有:N 1=N 2=N 3= 0。
aaaa13、图示桁架DE 杆的内力为零。
a a14、图示对称桁架在对称荷载作用下,其零杆共有三根。
15、图示桁架共有三根零杆。
16、图示结构的零杆有7根。
17、图示结构中,CD 杆的内力 N 1=-P 。
a 418、图示桁架中,杆1的轴力为0。
4a19、图示为一杆段的M 、Q 图,若Q 图是正确的,则M 图一定是错误的。
图M Q 图二、选择题1、对图示的AB 段,采用叠加法作弯矩图是:A. 可以;B. 在一定条件下可以;C. 不可以;D. 在一定条件下不可以。
2、图示两结构及其受载状态,它们的内力符合:A. 弯矩相同,剪力不同;B. 弯矩相同,轴力不同;C. 弯矩不同,剪力相同;D. 弯矩不同,轴力不同。
PPP2 l ll l3、图示结构M K(设下面受拉为正)为:A. qa22;B. -qa2;C. 3qa22;D. 2qa2。
2a4、图示结构M DC(设下侧受拉为正)为:A. -Pa;B.Pa;C. -Pa;D. Pa。
a a5、在径向均布荷载作用下,三铰拱的合理轴线为:A.圆弧线;B.抛物线;C.悬链线;D.正弦曲线。


第1章几何组成分析§1 – 1 基本概念1-1-1 名词解释●几何不变体系——结构(静定或超静定)在不考虑材料变形情况下,几何形状和位置不变的体系,称为几何不变体系。
●几何可变体系在不考虑材料变形情况下,形状或位置可变的体系,称为几何可变体系。
●刚片在平面上的几何不变部分。
●自由度确定体系位置所需的独立坐标数目。
●约束(联系)能够减少自由度的装置。
减少自由度的个数为约束个数。
①链杆——相当1个约束②铰——相当2个约束③虚铰——相当2个约束④复铰——相当n-1个单铰的作用●多余联系不能减少自由度的联系,称Array为多余联系。
●必要联系去掉时能够增加自由度(或维持体系不变性必须)的联系。
●瞬变体系几何特征:几何可变体系经过微小位移后成为几何不变体系。
静力特征:受很小的力将产生无穷大内力,因此不能作结构。
1-1-2 分析规则在不考虑材料应变所产生变形的条件下,构成无多余约束几何不变体系(静定结构)的基本规则如下:●三刚片规则三个刚片用不在同一条直线上的三个铰(或虚铰)两两相联。
●二刚片规则2结构力学典型例题解析两个刚片用不交于一点也不全平行的三根链杆相联;或:两个刚片用一个铰和不通过该铰心的链杆相联。
●二元体规则什么是二元体(二杆结点):两根不在同一条直线上的链杆联接一个新结点的装置,称为二元体。
在一个体系上增加或减少二元体不影响其几何不变性。
1-1-3 几何组成分析一般方法(步骤)(1)去二元体(二杆结点)。
(2)分析地基情况:上部体系与地基之间●当有满足二刚片规则的三个联系时,去掉地基,仅分析上部体系;●当少于三个联系时,必为几何常变体系;●当多于三个联系时,将地基当作一个刚片进行分析。
(3)利用规则找大刚片(最简单情况为:三个铰接杆件为刚片)。
(4)使用几何组成规则进行分析。
利用三刚片规则分析时:首先找出三个刚片,(满足三刚片规则的连接条件,即每两个刚片间有一个铰(或虚铰),然后再标出虚铰位置,最后看三个铰是否构成三角形。



静定桁架结构的内力分析——典型例题【例1】求如图1(a)所示桁架中所有杆件的轴力。
图1【解】(1)取截面Ⅰ-Ⅰ以右部分作研究,由有:,解得:从而有:(2)再依次由结点8、4、3、7、6、5、1的平衡条件,求得其它杆轴力,如图1(b)所示。
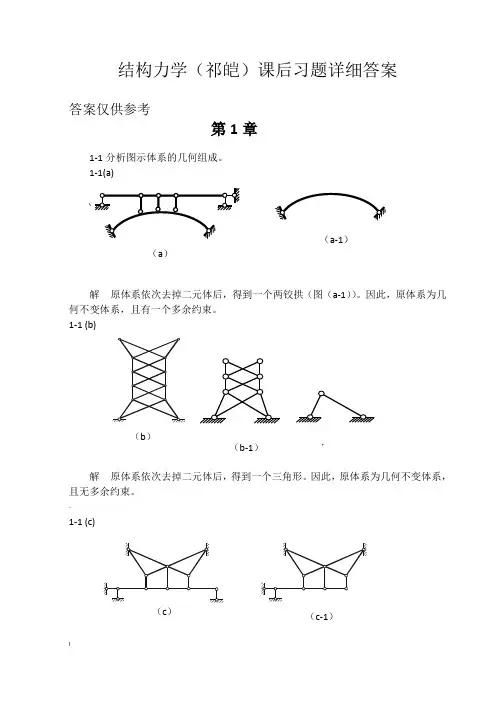
【例2】求如图2所示桁架中杆件a 、b 的轴力。
图2【解】经几何组成分析,此结构为三铰桁架。
(1)求支座反力取铰7右边部分为隔离体分析,由有:10M =∑89230x F d F d F d ⨯-⨯-⨯=892x F F=892)3N F F d ==拉力70M =∑22x y F F =由整体平衡条件有:从而有: , 再分别由整体平衡条件、有:, (2)作截面Ⅰ-Ⅰ,取左边作为隔离体研究,由得:(3)作截面Ⅱ-Ⅱ,取右边作为隔离体研究,由有:,解得: 从而得:。
【例3】求如图3所示桁架中杆件a 、b 的轴力。
图3【解】经几何组成分析,此结构为主从结构,截面Ⅰ-Ⅰ左边为附属部分,右边为基本部分。
杆件58、78为零杆。
(1)作截面Ⅰ-Ⅰ,取左边作为隔离体研究,由得:10M =∑2224x y F d F d F d ⨯+⨯=⨯()223x F F =←()223y F F =↑0x F =∑0y F =∑()123x F F =→()113y F F =↑0y F =∑()13Na F F =-压力80M =∑222xb x y F d F d F d ⨯+⨯=⨯23xb F F =-()Nb F =压力0y F =∑()1V F F =↑由整体平衡条件得 ,由有 (2)作截面Ⅱ-Ⅱ,取右边作为隔离体研究研究 由有:,从而得: 由有:,从而得:【例4】求如图5-7所示桁架中杆件a 、b 的轴力。
图4【解】(1)取截面Ⅰ-Ⅰ以上部分为隔离体分析,由有:,从而得:(2)取截面Ⅱ-Ⅱ以左部分为隔离体,由有:,从而得:【例5】求如图5(a)所示桁架中杆件a 、b 的轴力。
第2章 静定结构内力计算
§2 – 1 基本概念
2-1-1 支座反力(联系力)计算方法
●两刚片组成结构(单截面法)
满足两刚片规则的体系,两个刚片之间只有三个联系,可取出一个刚片作隔离体( 如图2-1c 或 如图2-1d ),联系力个数与独立平衡条件个数相等,利用平衡条件:
0x F =∑ 0y F =∑ 0M =∑
即可计算出两个刚片之间的三个联系力。
●三刚片组成结构(双截面法)
先求一个铰(或虚铰)的两个联系力。
切断两个铰(或虚铰)得到一个隔离体,有两种情况的隔离体。
首先,切断A 、B 铰得到第一个隔离体(如图2-2c),求B 铰的联系力,对A 铰取矩列平衡方程。
0A M =∑
然后,切断C 、B 铰得到第二个隔离
体(如图2-2d),求B 铰的联系力,对C 铰取矩列平衡方程。
0C M =∑
将上述两个平衡方程联立,即可求出B 铰的联系力。
(d)隔离体
2 图2-1 二刚片隔离体示意图
Bx
(c)隔离体
(b)三链杆情况
(a)一链杆一铰情况
图2-2 三刚片隔离体示意图
Ax (c)部分隔离体
(a)三刚片取1-1截面
(d)整体隔离体
(b)三刚片取2-2截面
4结构力学典型例题解析
●基附型结构(先附后基)
所谓基本部分就是直接与地基构成几何不变体系的部分;而不能与地基直接构成几何不变体系的部分称为附属部分,这类型结构称为基附型结构。
由于基本部分除了具备和地基构成几何不变所需要的联系外,还与附属部分有联系,若先取基本部分作隔离体,未知力的个数将很多。
而附属部分的联系就比较少,因此,先选取附属部分作为隔离体进行求解,最后求解基本部分。
对于基附结构求解顺序是:先附后基。
2-1-2 快速弯矩图方法
●利用微分关系
(1)无外荷载的直杆段,剪力为常数,弯矩图为直线;
(2)无外荷载的直杆段,若剪力为零,则弯矩图为常数;
(3)铰(或自由端)附近无外力偶作用时,铰(或自由端)附近弯矩为零;
有外力偶作用时,铰(或自由端)附近弯矩等于外力偶;
(4)直杆段上有荷载时,弯矩图的凸向与荷载方向一致;
(5)直杆段上仅有集中力偶作用时,剪力不变,弯矩图有突变但斜率相同。
●悬臂梁法作弯矩图
一端自由的直杆件,当将刚结点当作固定端时,如果得到悬臂梁,那么该杆件可以当作悬臂梁作弯矩图。
将这种作弯矩图的方法称为悬臂梁法。
●简支梁法(区段叠加法)作弯矩图
从结构中任意取出的一个直杆段,若直杆段两端的弯矩已知,将两端弯矩当作外荷载(力偶),可以将该直杆段及其上作用的荷载一起放到简支梁上,得到一个简支梁,该直杆段可以按照简支梁方法作弯矩图。
将这种作弯矩图的方法称为简支梁法。
●利用刚结点力矩平衡
取刚结点作隔离体,利用力矩平衡条件可得到如下结论:
(1)当刚结点连接两个杆件,无外力偶作用时,两个杆端弯矩一定等值同侧。
(2)连接刚结点的杆件只有一个杆端弯矩未知时,利用力矩平衡条件可以求出。
●几种结点的内力特点
(1)铰结点传递剪力但不传递弯矩;
(2)与杆轴线一致的定向结点传递弯矩但不传递剪力;
(3)与杆轴线垂直的定向结点传递弯矩但不传递轴力;
(4)与杆轴线一致的链杆结点传递轴力,但不传递弯矩和剪力;
(5)与杆轴线垂直的链杆结点传递剪力,但不传递弯矩和轴力。
2-1-3 桁架特殊内力的计算
●桁架零杆判断
如图2-3所示的两种杆件轴力为零的情况(可利用平衡条件证明)。
第2章 静定结构内力计算 3
●对称桁架的对称性利用
2-1-4 已知弯矩图求剪力
●取直杆段作为隔离体(如图2-5),已知杆端弯矩,AB BA M M 和杆端上的外荷载; 两个杆端剪力Q Q ,AB
BA F
F 和两个杆端轴力N N ,AB BA F F 共计四个未知力。
●利用平衡条件即可求出杆端剪力Q Q ,AB
BA F
F :
(1)列力矩方程
0B
M =∑
可得A 端剪力Q AB
F
(2)列投影方程
0y
F
=∑
可得B 端剪力Q BA
F
●注意:已知弯矩图求剪力的方法,只要直杆件,不论静定结构还是超静定结构上述方法都适用。
本方法在位移法中也经常使用,求解有线位移的超静定结构,需要计算附加链杆反力,附加链杆反力的计算首先需要杆件剪力,有了剪力之后通过对合适的隔离体列投影平衡条件即可求出附加链杆反力。
图2-3 桁架零内力杆件
图2-4 对称桁架的零内力杆件
对称轴
对称荷载
反对称荷载
反对称荷载
(a)
(b)
(c)
N BA
图2-5 直杆段求剪力隔离体图
F
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3
4结构力学典型例题解析
第2章静定结构内力计算3。