静定结构位移计算练习题

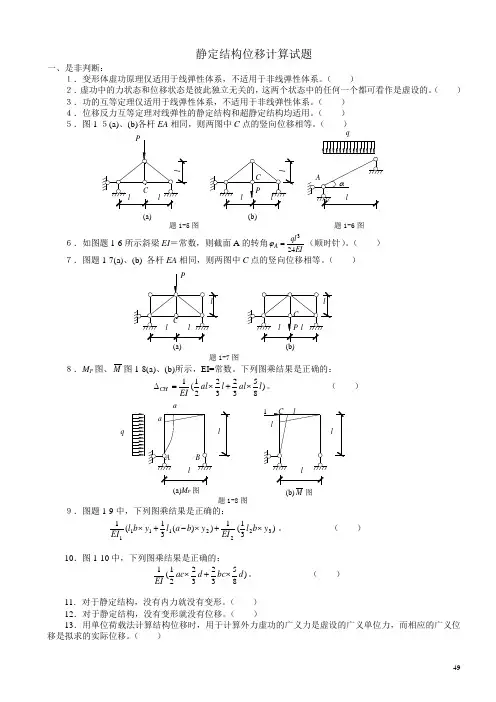
静定结构位移计算试题一、是非判断：１．变形体虚功原理仅适用于线弹性体系，不适用于非线弹性体系。

（ ） ２．虚功中的力状态和位移状态是彼此独立无关的，这两个状态中的任何一个都可看作是虚设的。

（ ） ３．功的互等定理仅适用于线弹性体系，不适用于非线弹性体系。

（ ） ４．位移反力互等定理对线弹性的静定结构和超静定结构均适用。

（ ） ５．图1-５(a)、(b)各杆EA 相同，则两图中C 点的竖向位移相等。

（ ）题1-5图 题1-6图６．如图题1-6所示斜梁EI ＝常数，则截面A 的转角EIql A 243=ϕ（顺时针）。

（ ） ７．图题1-7(a)、(b) 各杆EA 相同，则两图中C 点的竖向位移相等。

（ ）题1-7图８．M P 图、M 图1-8(a)、(b)所示，EI=常数。

下列图乘结果是正确的：)85323221(1l al l al EI CH ⨯+⨯=∆。

（ ）题1-8图 ９．图题1-9中，下列图乘结果是正确的：)31(1))(31(132221111y b l EI y b a l y b l EI ⨯+⨯-+⨯。

（ ）10．图1-10中，下列图乘结果是正确的：)85323221(1d bc d ac EI ⨯+⨯。

（ ）11．对于静定结构，没有内力就没有变形。

（ ） 12．对于静定结构，没有变形就没有位移。

（ ）13．用单位荷载法计算结构位移时，用于计算外力虚功的广义力是虚设的广义单位力，而相应的广义位移是拟求的实际位移。

（ ）q(a)(b)l a aqABP (b)M 图题1-9图 题1-10图14．如果结构是由线弹性材料制成的，但在有温度变化的情况下，功的互等定理不成立。

（ ） 二、填空1．虚功原理有两种不同的应用形式，即 原理和 原理。

其中 原理等价于变形协调条件。

2．位移计算时，虚拟广义单位力的原则是使外力虚功的值恰好等于 值。

3．用图乘法计算梁和刚架位移的适用条件是 。

4．如图2-4所示结构支座A 下沉a ，支座B 向右移动b ，则结点C 、D 的相对转角为 。

第5章静定结构位移计算的虚力法
5.1 复习笔记
本章重点介绍了虚力法的原理以及如何运用虚力法对不同结构在各种荷载作用下的指定位移进行求解。

遵循“化整为零、积零为整”的思想，对结构的局部位移公式进行了分项讨论，在虚力法的指导下叠加组成了结构的整体变形公式，随后将虚力法升华到了对广义单位荷载的设定以及对广义位移的求解；通过引入图乘法，结构的弯矩变形公式的求解变得更加快捷且精确；最后介绍了温度影响下结构的位移求解并归纳了线性变形体系的四个互等定理。

一、虚力法求刚体体系的位移（见表5-1-1）
表5-1-1 虚力法求刚体体系的位移
图5-1-1
二、虚力法求静定结构的位移（见表5-1-2）
表5-1-2 虚力法求静定结构的位移
表5-1-3 广义位移分类
三、两个对偶解法——虚力法求位移、虚位移法求内力（见表5-1-4）
表5-1-4 两个对偶解法——虚力法求位移、虚位移法求内力
四、荷载作用时静定结构的弹性位移计算（见表5-1-5）
表5-1-5 荷载作用时静定结构的弹性位移计算
五、图乘法（见表5-1-6）
表5-1-6 图乘法
图5-1-2 六、温度改变时静定结构位移计算（见表5-1-7）。

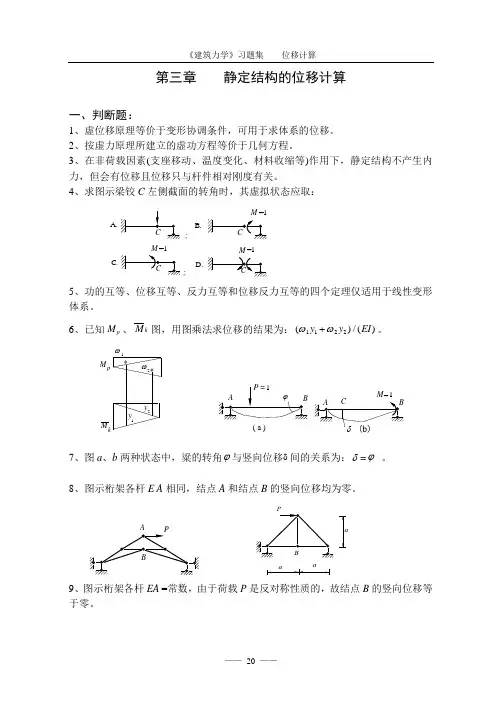
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形协调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A两侧截面的相对转角ϕA，EI = 常数。

q11、求图示静定梁D端的竖向位移∆DV。

EI = 常数，a = 2m 。

10kN/m12、求图示结构E点的竖向位移。

EI = 常数。

q13、图示结构，EI=常数，M=⋅90kN m, P = 30kN。

求D点的竖向位移。

P14、求图示刚架B端的竖向位移。

q15、求图示刚架结点C的转角和水平位移，EI = 常数。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝ 常数 。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI ＝ 常数 。

18、求图示刚架中D 点的竖向位移。

E I = 常数 。

ql l l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI ＝ 常数 。

l/23l/320、求图示结构A 、B 两点的相对水平位移，E I = 常数。

21、求图示结构B 点的竖向位移，EI = 常数 。

l l22、图示结构充满水后，求A 、B 两点的相对水平位移。

E I = 常数 ，垂直纸面取1 m 宽，水比重近似值取10 kN / m 3。

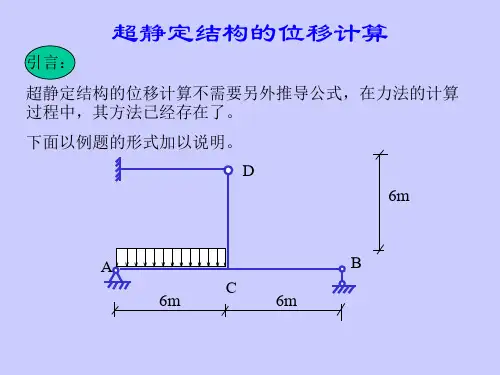
静定结构的位移计算第4章 静定结构的位移计算4.1 结构位移的概念4.1.1 结构位移结构都是由变形材料制成的，当结构受到外部因素的作用时，它将产生变形和伴随而来的位移。

变形是指形状的改变，位移是指某点位置或某截面位置和方位的移动。

如图 4.1(a)所示刚架,在荷载作用下发生如虚线所示的变形，使截面A 的形心从A 点移动到了A ′点，线段AA ′称为A 点的线位移，记为A ∆，它也可以用水平线位移Ax ∆和竖向线位移Ay ∆两个分量来表示如图4.1(b)。

同时截面A 还转动了一个角度，称为截面A 的角位移，用A ϕ表示。

又如图4.2所示刚架，在荷载作用下发生虚线所示变形，截面A 发生了A ϕ角位移。

同时截面B 发生了B ϕ的角位移，这两个截面的方向相反的角位移之和称为截面A 、B 的相对角位移，即B A AB ϕϕϕ+=。

同理，C 、D 两点的水平线位移分别为C ∆如D ∆，这两个指向相反的水平位移之和称为C 、D 两点的水平相对线位移，既D C CD ∆+∆=∆。

除上述位移之外，静定结构由于支座沉降第4章静定结构的位移计算70等因素作用，亦可使结构或杆件产生位移，但结构的各杆件并不产生内力，也不产生变形，故把这种位移称为刚体位移。

一般情况下，结构的线位移、角位移或者相对位移，与结构原来的几何尺寸相比都是极其微小的。

4.1图71第4章静定结构的位移计算引起结构产生位移的主要因素有：荷载作用、温度改变、支座移动及杆件几何尺寸制造误差和材料收缩变形等。

4.1.2 结构位移计算的目的1. 验算结构的刚度结构在荷载作用下如果变形太大，即使不破坏也不能正常使用。

既结构设计时，要计算结构的位移，控制结构不能发生过大的变形。

让结构位移不超过允许的限值，这一计算过程称为刚度验算。

2. 解算超静定计算超静定结构的的反力和内力时，由于静力平衡方程数目不够，需建立位移条件的补充方程，所以必须计算结构的位移。

3. 保证施工在结构的施工过程中，也常常需要知道结构的位移，以确保施工安全和拼装就位。

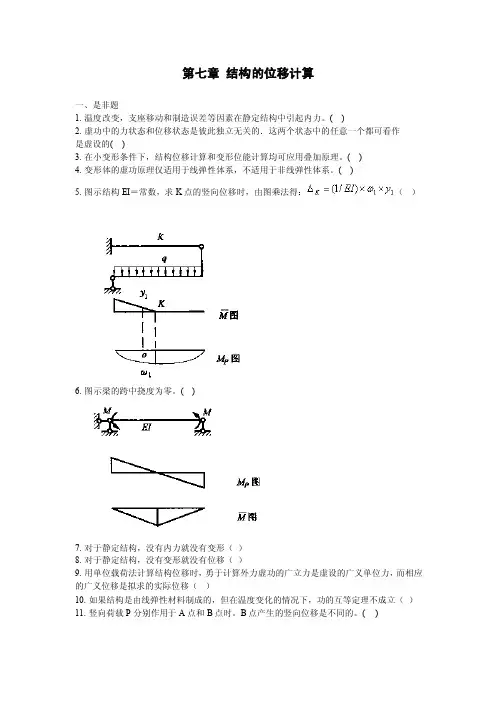
第七章结构的位移计算一、是非题1. 温度改变，支座移动和制造误差等因素在静定结构中引起内力。

( )2. 虚功中的力状态和位移状态是彼此独立无关的．这两个状态中的任意一个都可看作是虚设的( )3. 在小变形条件下，结构位移计算和变形位能计算均可应用叠加原理。

( )4. 变形体的虚功原理仅适用于线弹性体系，不适用于非线弹性体系。

( )5. 图示结构EI＝常数，求K点的竖向位移时，由图乘法得：（）6. 图示梁的跨中挠度为零。

( )7. 对于静定结构，没有内力就没有变形（）8. 对于静定结构，没有变形就没有位移（）9. 用单位载荷法计算结构位移时，勇于计算外力虚功的广立力是虚设的广义单位力，而相应的广义位移是拟求的实际位移（）10. 如果结构是由线弹性材料制成的，但在温度变化的情况下，功的互等定理不成立（）11. 竖向荷载P分别作用于A点和B点时。

B点产生的竖向位移是不同的。

( )12.变形体体系虚功方程推导过程中，微元体上外力的刚体位移总虚功为零，是基于变形协调条件（）13. 图(a)和图(b)两弯矩图图乘结果为（）14.功的互等定理、位移互等定理、反力互等定理只适用于线弹性体系。

〔 )15.计算静定结构由于温度改变引起的位移时，不计剪切变形项是由于剪力较小。

( )二、填空题1. 图示桁架各杆EA相同，C点承受水平荷载P后，则CA和CB杆的夹角的改变量为______。

2. 图示刚架中，C、D两点的相对线位移等于______，两点距离______。

3. 虚功原理有两种不同的应用形式，即___________原理和_____________原理，其中_____________原理等价于变形协调条件。

4. 应用图乘法求杆件结构的位移时，各图乘的杆段必须满足如下三个条件：_________；_________；_________5. 结构与荷载如图所示，各杆EI相同，铰C处的竖向位移为________6. 图示刚架C点的竖向位移求得为，如各杆刚度EI减小一倍，C点的竖向位移为_________。

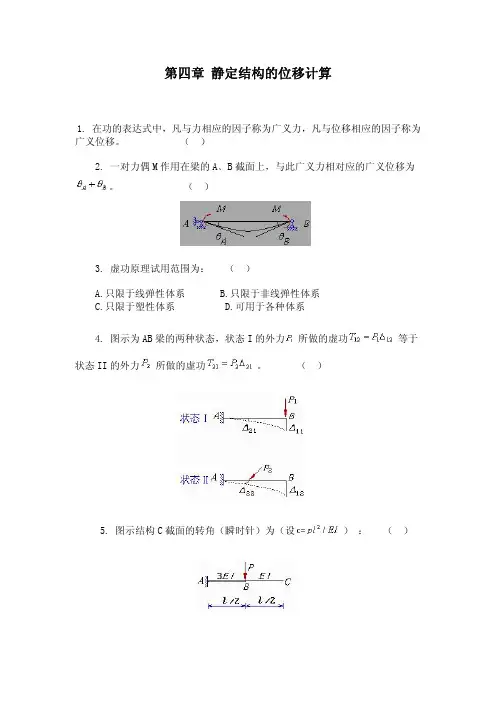
第四章 静定结构的位移计算1. 在功的表达式中，凡与力相应的因子称为广义力，凡与位移相应的因子称为广义位移。

（ ）2. 一对力偶M作用在梁的A﹑B截面上，与此广义力相对应的广义位移为。

（ ）3. 虚功原理试用范围为： （ ）A.只限于线弹性体系B.只限于非线弹性体系C.只限于塑性体系D.可用于各种体系4. 图示为AB梁的两种状态，状态I的外力 所做的虚功 等于状态II的外力 所做的虚功 。

（ ）5. 图示结构C截面的转角（瞬时针）为（设 ） ： （ ）A.c/8B.c/2C.c/24D.c/126. 图示桁架支座A下沉Δ，由此引起的D﹑E两截面的相对转角是为零。

（ ）7. 图示结构C截面的转角为（顺时针）：8. 图示对称桁架EA=常数，在给定荷载作用下AB两点竖向位移都为零。

（ ）9. 结构与荷载如图所示，各杆刚度EI相同，铰C的竖向位移为：( )10. 图示梁支座B下移 ，截面E的转角位移为（逆时针）： ( )11. 欲求图示结构铰C两侧截面的相对转角，其虚拟状态应取 ：（ ）12. 图示为梁的 图，曲线为二次抛物线，刚度为EI。

C点的竖向（向下）位移为（设 ）： ( )13. 图示三铰刚架EI=常数，铰C处的竖向位移为零。

（ ）14. 图示刚架C点的竖向位移为Δ，如各杆的刚度减少1/2, C点的竖向位移为：( )15. 图示刚架中，C﹑D两点相对线位移 。

（ ）16. 变形体虚功方程的推导过程中，微元体上外力的刚性位移总虚功为零是基于变形协调条件。

（ ）17. 图示刚架支座A发生倾角（顺时针），由此引起的B点的水平位移等于(向右)。

（ ）18. 图示梁为矩形截面，其高为h，材料的线膨胀系数为 ，温度变化如图所示， 梁中点的竖向位移为：19. 图（a）所示刚架的 图，如图（b），各杆EI相同，杆长均为4m，刚结点B的水平位移为：20. 结构与温度变化如图所示，AC杆的温差t=（ ）摄氏度。

一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。

（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。

（ ）3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。

（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。

（ ）二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分） 1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ）A ．2/M ；B ．M ；C ．0； D. )2/(EI M 。

2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。

（ ）( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线； B.结构可分为等截面直杆段； C.所有杆件EI 为常数且相同； D.结构必须是静定的。

( ) 5. （本小题3分）图示梁A 点的竖向位移为（向下为正）：( ) Ａ．F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三（本大题 5分）对图示体系进行几何组成分析。

A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。

土木工程力学（本）综合练习一、判断题1图示为刚架的虚设力状态，按此力状态及位移计算公式可求出A处的转角。

（×）A2．图示结构用位移法计算的基本未知量是3。

（×）3．超静定结构的力法基本结构是唯一的。

（×）4．汇交于某结点各杆端的力矩分配系数之比等于各杆端转动刚度之比。

（√）5．超静定结构的内力与材料的性质无关。

（×）6．力法典型方程的等号右端项不一定为0。

（√）7．对称结构在反对称荷载作用下，对称轴穿过的截面只有反对称的内力。

（√）8．在结构动力计算中，振动体系的振动自由度等于质点的数目。

（×）9．静定结构的内力和反力与杆件截面的几何尺寸有关。

（√）10．静定结构弯矩影响线是由直线段组成的。

√二、单项选择题1．简支梁某截面K弯矩影响纵坐标y K的物理意义是（ C ）。

M K影影影A 单位荷载的位置 B 截面K的位置C 截面K的弯矩D A、C同时满足C ）A 3B 4C 5D 63．超静定结构产生内力的原因（D ）A 荷载作用B 支座位移C 温度变化D 以上原因都可以4．结构位移计算时虚设力状态中的荷载可以是：（ D ）A 任意值（除0外）B 1C 正数D 负数5．结构位移计算公式利用什么推导的（C ）A 功的互等定理B 虚位移原理C 虚功原理D 反力互等定理6．用位移法计算超静定结构时，独立的结点角位移数等于（ D ）A 铰结点数B 刚结点数C 多余约束数D 不确定7．在图示结构中，使体系自振频率ω减小，可以（ C ）A 减小PF B 减小mC 减小EID 减小ll m t8．求图示结构AB两点的相对线位移，虚设力状态为图（ A ）ABM=1M=1A B C D1=F9．与杆件的传递弯矩有关的是（D ）A 分配弯矩B 传递系数C 分配系数D 结点位移10．用位移法解超静定结构其基本未知量的数目等于（A ）A 独立的结点位移数目B 刚结点数目C 线位移数目 D超静定次数三、作图题1.作图示静定梁的弯矩图。

静定结构的位移计算——典型例题【例1】计算如图1(a)所示梁结构中跨中C 点的竖向位移，已知EI 为常数。

【解】方法一：（积分法）（1）荷载作用的实际状态以及坐标设置如图6-8(a)，其弯矩方程为：（2）虚设单位力状态，以及坐标设置如图6-8(b)，其弯矩方程为：（3）积分法求跨中的竖向位移图1方法二：图乘法（1）荷载作用的实际状态，其弯矩图如图1(c)所示； （2）虚设单位力状态，其弯矩图如图1(d)所示； （3）图乘计算跨中竖向位移【例2】计算如图2(a)所示半圆曲梁中点C 的竖向位移，只考虑弯曲变形。

已知圆弧半径为R ，EI 为常数。

CV ∆21102211112222P qlx x l M qlx q x l l x l ⎧⎛⎫≤≤ ⎪⎪⎝⎭⎪=⎨⎛⎫⎛⎫⎪--<≤ ⎪ ⎪⎪⎝⎭⎝⎭⎩1021122x x l M l l x l ⎧⎛⎫≤≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪<≤ ⎪⎪⎝⎭⎩24/20/211111113()22222232l l P CVl MM ql ds x qlxdx l qlx q x l dx EI EI EI EI ⎡⎤⎛⎫∆==⨯⨯+⨯⨯--=↓⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⎰⎰⎰4222211112111311121113()222432284223232232cPCV A y MM ds EI EI ql l ql l ql ql l l l ql l EI EI EI ω∆==⎡⎤⎛⎫⎛⎫=⨯⨯⨯⨯+⨯+⨯⨯+⨯⨯⨯=↓ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∑⎰CV ∆图2【解】（1）实际荷载作用下，以任意半径与x 轴的顺时针夹角θ为自变量（图2a ），弯矩方程为（截面内侧受拉为正）：（2）虚设单位荷载状态如图2(b)所示，其弯矩方程为：（3）积分法求跨中的竖向位移【例3】如图3(a)所示梁的EI 为常数，在荷载F 作用下测得结点E 的竖向位移为9mm （向下），求截面B 处的角位移。